2024-2025学年河北省石家庄市无极县文苑中学高二(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年河北省石家庄市无极县文苑中学高二(上)开学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 123.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-14 00:00:00 | ||
图片预览



文档简介
2024-2025学年河北省石家庄市无极县文苑中学高二(上)开学
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知平面向量,,,若,则实数的值为( )
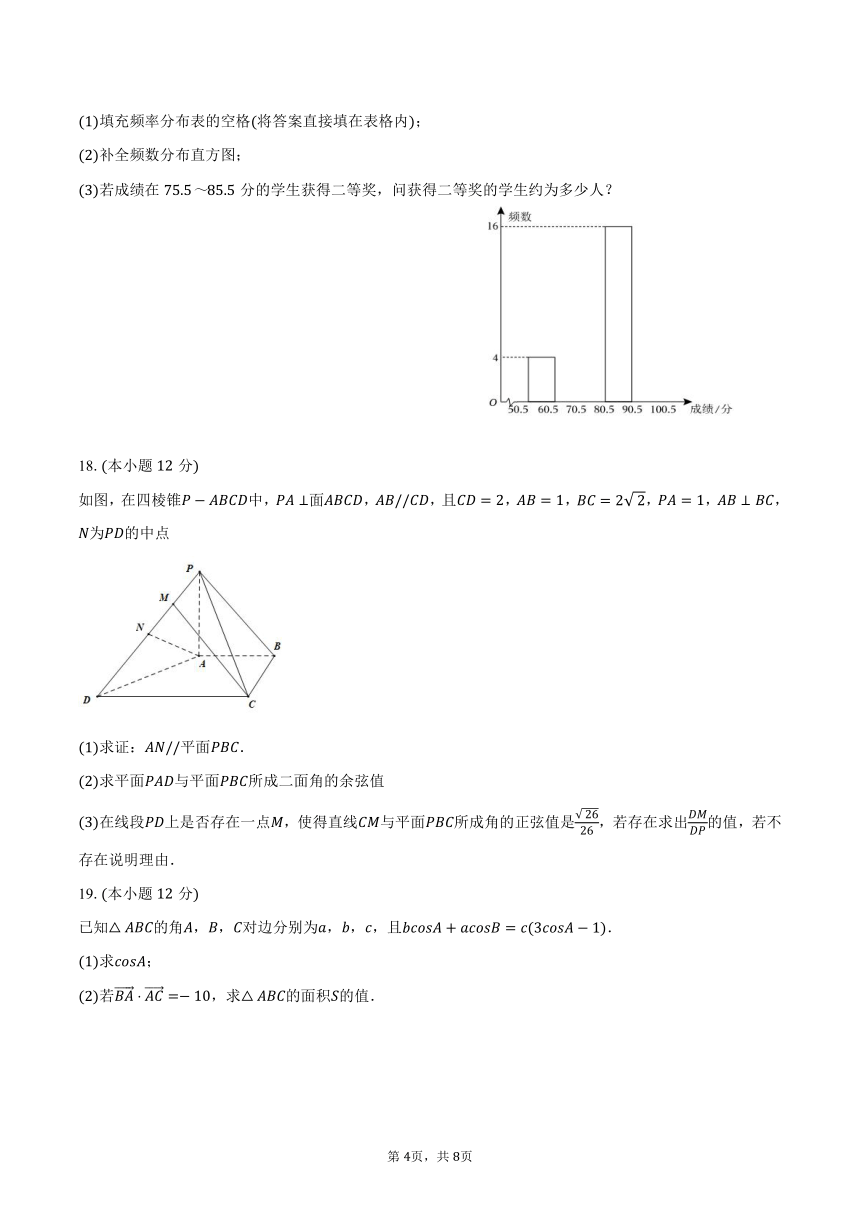
A. B. C. D.
2.设复数是虚数单位,则( )
A. B. C. D.
3.在平行四边形中,,且,,若将其沿折起使平面平面,则三棱锥的外接球的表面积为( )
A. B. C. D.
4.如图,已知边长为的正方体,点为线段的中点,则直线与平面所成角的正切值为( )
A. B.
C. D.
5.我市对上、下班交通情况作抽样调查,上、下班时间各抽取辆机动车测其行驶速度单位:如下表:
上班时间
下班时间
则上、下班时间行驶时速的中位数分别为( )
A. 与 B. 与 C. 与 D. 与
6.已知个数,,的平均数为,方差为,则数,,的平均数和方差分别为( )
A. , B. , C. , D. ,
7.正方形与等腰直角三角形所在的平面互相垂直,且,,,分别是线段,的中点,则与所成的角的余弦值为( )
A. B.
C. D.
8.在中,为的中点,为线段上靠近的三等分点,则( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.设点是所在平面内一点,则下列说法正确的是( )
A. 若,则点是的重心
B. 若,则点在边的延长线上
C. 若在所在的平面内,角、、所对的边分别是,,,满足以下条件,则
D. 若,且,则的面积是面积的
10.如图,在正六边形中,点为其中心,则下列判断正确的是( )
A.
B.
C.
D.
11.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了年月至年月期间月接待游客量单位:万人的数据,绘制了下面的折线统计图根据该折线统计图,下列结论正确的是( )
A. 年接待游客量逐年增加
B. 各年的月接待游客量高峰期大致都在月
C. 年月至月月接待游客量逐月增加
D. 各年月至月的月接待游客量相对于月至月,波动性更小,变化比较平稳
三、填空题:本题共3小题,每小题5分,共15分。
12.设向量,,且,则 ______.
13.在中,内角,,的对边分别是,,,角等于,若,,则的长为______.
14.鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根等长的正四棱柱体分成三组,经榫卯起来.若正四棱柱的高为,底面正方形的边长为,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为_______容器壁的厚度忽略不计,结果保留
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知,,.
求与的夹角;
当为何值时,向量的模长为?
16.本小题分
已知复数,且纯虚数.
求复数;
若,求复数的模.
17.本小题分
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有名学生参加了这次竞赛为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计请根据尚未完成的频率分布表和频数分布直方图,解答下列问题.
分组 频数 频率
合计
填充频率分布表的空格将答案直接填在表格内;
补全频数分布直方图;
若成绩在分的学生获得二等奖,问获得二等奖的学生约为多少人?
18.本小题分
如图,在四棱锥中,面,,且,,,,,为的中点
求证:平面.
求平面与平面所成二面角的余弦值
在线段上是否存在一点,使得直线与平面所成角的正弦值是,若存在求出的值,若不存在说明理由.
19.本小题分
已知的角,,对边分别为,,,且.
求;
若,求的面积的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:因为,,.
所以,,
所以,又,所以.
若向量的模长为,
则,
解得或.
16.解:,且为纯虚数,
得,即,;
若,则.
17.解:频率分布表:
分组 频数 频率
合计
频数分布直方图如下图所示:
成绩在分的学生占分的学生的,
因为成绩在分的学生频率为,
所以成绩在分的学生频率为,
成绩在分的学生占分的学生的,
因为成绩在分的学生频率为,
所以成绩在分的学生频率为,
所以成绩在分的学生频率为,
由于有名学生参加了这次竞赛,
所以该校获得二等奖的学生约为人.
18.解:过作,垂足为,则,以为坐标原点,分别以所在直线为轴建立空间直角坐标系,
则
,
, 则,
设平面的一个法向量为,
,, 取
,
,
又,
设平面的一个法向量为,
,
,取,
,
所成锐二面角的余弦值
令,设,
,
,
平面的一个法向量 ,
,
,
,
,
,
19.解:在中,,
利用正弦定理:,
整理得:;
由于,
所以,
整理得;
所以.
第1页,共1页
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知平面向量,,,若,则实数的值为( )
A. B. C. D.
2.设复数是虚数单位,则( )
A. B. C. D.
3.在平行四边形中,,且,,若将其沿折起使平面平面,则三棱锥的外接球的表面积为( )
A. B. C. D.
4.如图,已知边长为的正方体,点为线段的中点,则直线与平面所成角的正切值为( )
A. B.
C. D.
5.我市对上、下班交通情况作抽样调查,上、下班时间各抽取辆机动车测其行驶速度单位:如下表:
上班时间
下班时间
则上、下班时间行驶时速的中位数分别为( )
A. 与 B. 与 C. 与 D. 与
6.已知个数,,的平均数为,方差为,则数,,的平均数和方差分别为( )
A. , B. , C. , D. ,
7.正方形与等腰直角三角形所在的平面互相垂直,且,,,分别是线段,的中点,则与所成的角的余弦值为( )
A. B.
C. D.
8.在中,为的中点,为线段上靠近的三等分点,则( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.设点是所在平面内一点,则下列说法正确的是( )
A. 若,则点是的重心
B. 若,则点在边的延长线上
C. 若在所在的平面内,角、、所对的边分别是,,,满足以下条件,则
D. 若,且,则的面积是面积的
10.如图,在正六边形中,点为其中心,则下列判断正确的是( )
A.
B.
C.
D.
11.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了年月至年月期间月接待游客量单位:万人的数据,绘制了下面的折线统计图根据该折线统计图,下列结论正确的是( )
A. 年接待游客量逐年增加
B. 各年的月接待游客量高峰期大致都在月
C. 年月至月月接待游客量逐月增加
D. 各年月至月的月接待游客量相对于月至月,波动性更小,变化比较平稳
三、填空题:本题共3小题,每小题5分,共15分。
12.设向量,,且,则 ______.
13.在中,内角,,的对边分别是,,,角等于,若,,则的长为______.
14.鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,它的外观是如图所示的十字立方体,其上下、左右、前后完全对称,六根等长的正四棱柱体分成三组,经榫卯起来.若正四棱柱的高为,底面正方形的边长为,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积至少为_______容器壁的厚度忽略不计,结果保留
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知,,.
求与的夹角;
当为何值时,向量的模长为?
16.本小题分
已知复数,且纯虚数.
求复数;
若,求复数的模.
17.本小题分
为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有名学生参加了这次竞赛为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩进行统计请根据尚未完成的频率分布表和频数分布直方图,解答下列问题.
分组 频数 频率
合计
填充频率分布表的空格将答案直接填在表格内;
补全频数分布直方图;
若成绩在分的学生获得二等奖,问获得二等奖的学生约为多少人?
18.本小题分
如图,在四棱锥中,面,,且,,,,,为的中点
求证:平面.
求平面与平面所成二面角的余弦值
在线段上是否存在一点,使得直线与平面所成角的正弦值是,若存在求出的值,若不存在说明理由.
19.本小题分
已知的角,,对边分别为,,,且.
求;
若,求的面积的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:因为,,.
所以,,
所以,又,所以.
若向量的模长为,
则,
解得或.
16.解:,且为纯虚数,
得,即,;
若,则.
17.解:频率分布表:
分组 频数 频率
合计
频数分布直方图如下图所示:
成绩在分的学生占分的学生的,
因为成绩在分的学生频率为,
所以成绩在分的学生频率为,
成绩在分的学生占分的学生的,
因为成绩在分的学生频率为,
所以成绩在分的学生频率为,
所以成绩在分的学生频率为,
由于有名学生参加了这次竞赛,
所以该校获得二等奖的学生约为人.
18.解:过作,垂足为,则,以为坐标原点,分别以所在直线为轴建立空间直角坐标系,
则
,
, 则,
设平面的一个法向量为,
,, 取
,
,
又,
设平面的一个法向量为,
,
,取,
,
所成锐二面角的余弦值
令,设,
,
,
平面的一个法向量 ,
,
,
,
,
,
19.解:在中,,
利用正弦定理:,
整理得:;
由于,
所以,
整理得;
所以.
第1页,共1页
同课章节目录
