8.4 机械能守恒定律(共18张ppt)
文档属性
| 名称 | 8.4 机械能守恒定律(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 13.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-14 21:50:55 | ||
图片预览





文档简介
(共19张PPT)
第四章 机械能守恒定律
一、何为"守恒"
即"保持不变"
生活中有没有"守恒"呢
一共有10瓶矿泉水,可以按不同的方法分给两人。
若甲分得8瓶 则乙分得2瓶
弱甲分得7瓶 则乙分得3瓶
若甲分得6瓶 则乙分得4瓶
若甲分得5瓶 则乙分得5瓶
1.在此过程中,“守恒量”是什么?
矿泉水的总量
2.如何求出这个“守恒量”呢?
选择其中一次进行相加
思考:从上个问题中可以得出,“守恒规律”有什么样的特点?
1.守恒过程对应某一过程的各个状态
2.守恒规律对应某一种相同的物理量
3.守恒规律可以表达为形如a=a的形式
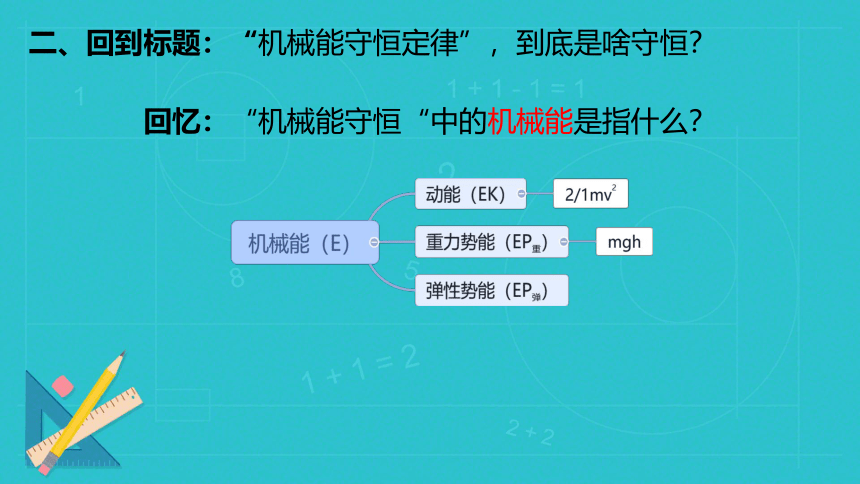
二、回到标题:“机械能守恒定律”,到底是啥守恒?
回忆:“机械能守恒“中的机械能是指什么?
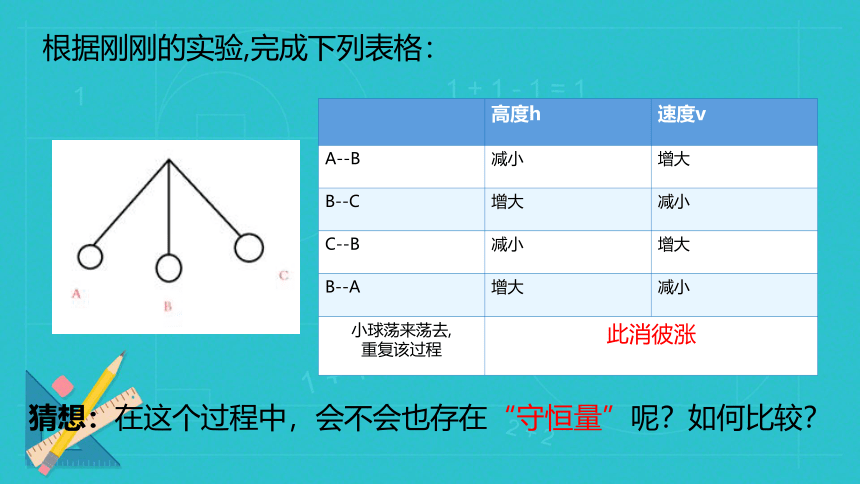
小球的运动有什么规律?小球在运动过程中,h、v怎么变?
高度h 速度v
A--B 减小 增大
B--C 增大 减小
C--B 减小 增大
B--A 增大 减小
小球荡来荡去, 重复该过程 此消彼涨
根据刚刚的实验,完成下列表格:
猜想:在这个过程中,会不会也存在“守恒量”呢?如何比较?
三、验证猜想
①亏了。猪肉比牛肉便宜,换成猪肉的话,肉的总价值可能减少了。
②赚了。换到的猪肉比牛肉要多,这样能吃得更加饱。
③赚/亏了。猪肉(牛肉)比牛肉(猪肉)更好吃。
在比较时,应该将要比较的值,转化成单位相同的量来比较
脑筋急转弯:2斤牛肉,换5斤猪肉,是亏了还是赚了?
重力势能变化 动能变化
A--B 减小 增大
B--C 增大 减小
C--B 减小 增大
B--A 增大 减小
小球荡来荡去, 重复该过程 此消彼涨
探究:重力势能和动能的转化
思考:在小球摆动的过程中,重力势能和动能是否完全相互转化?
小球的机械能是否守恒?
四、猜想与验证:小球在摆动过程中的动能与重力势能没有发生完全的转化,
那么是什么原因导致损耗的?
在单摆上的小铁球旁加上塑料球、泡沫球,让它们从同一高度释放,
观察各种小球的运动情况,分析其受力及其做功情况。
材料 泡沫球 塑料球 钢球
受力情况 重力/拉力/很大阻力 重力/拉力/较小阻力 重力/拉力/很小阻力
做功情况 重力做功/阻力做功很多 重力做功/阻力做功较少 重力做功/阻力做功很少
机械能变化情况 减小得很快 减小较快 减少很慢
由此可推导出:若完全没有阻力做功(即只有重力做功),动能和重
力势能转化的过程中,总的机械能不变。
推一下它可以吗?
你能用公式证明上面的结论吗?
小球从1--2 的过程中,机械能转化情况如何?
WG=Ep1-Ep2
WG-Wf=EK2-EK1,
联立得:
Ep1-Ep2-Wf=EK2-EK1
Ep1+EK1=Ep2+EK2+Wf
E1≠E2
若Wf=0,则E1=E2
五、探究:动能与弹性势能的转化
分析:在滑块运动过程中,其动能和弹性势能的转化情况如何?
运动过程 Ep弹变化 EK变化
A--B 减小 增大
B--C 增大 减小
C--B 减小 增大
B--A 增大 减小
循环往复 此消彼涨
受哪些力 哪些力做功
滑块 重力、支持力、弹簧弹力、阻力 弹簧弹力做功、阻力做功很少
此时的机械能
守恒吗?
与上个实验一样,你能用公式表示出系统的机械能变化情况吗?
WG=Ep1-Ep2
WG-Wf=EK2-EK1,
联立得:
Ep1-Ep2-Wf=EK2-EK1
Ep1+EK1=Ep2+EK2+Wf
E1≠E2
W弹=Ep弹1-Ep弹2
W弹-Wf=EK2-EK1,
联立得:
Ep弹1-Ep弹2-Wf=EK2-EK1
Ep弹1+EK1=Ep弹2+EK2+Wf
E1≠E2
若Wf=0,则机械能守恒。
结论:若只有弹簧弹力做功,动能和弹性势能转化过程中,
总的机械能守恒。
探究:动能和重力势能、弹性势能的转化规律
W弹=Ep弹1-Ep弹2
W弹-Wf=EK2-EK1,
联立得:
Ep弹1-Ep弹2-Wf=EK2-EK1
Ep弹1+EK1=Ep弹2+EK2+Wf
E1≠E2
W弹=Ep弹1-Ep弹2
WG=Ep1-Ep2
WG+W弹-Wf=EK2-EK1,
联立得:
Ep1-Ep2+Ep弹1-Ep弹2-Wf=EK2-EK1
Ep1+Ep弹1+EK1=Ep弹2+EK2+Ep2+Wf
E1≠E2
若Wf=0,则机械能守恒
注意! 机械能守恒,指的是重物的机械能守恒吗?
指重物、地球、弹簧所组成的系统机械能守恒
课堂小结:机械能守恒定律
机械能守恒定律
1.内容:在只有重力或者弹力做功的系统内,动能与势能可以相互转化,而总的机械能保持不变。
2.机械能为守恒量,即机械能保持不变。
3.表达式:E1=E2,Ep1+EK1=Ep2+EK2
生活中的守恒
1.守恒过程对应某一过程的各个状态
2.守恒规律对应某一种相同的物理量
3.守恒规律可以表达为形如a=a的形式
谢 谢!
第四章 机械能守恒定律
一、何为"守恒"
即"保持不变"
生活中有没有"守恒"呢
一共有10瓶矿泉水,可以按不同的方法分给两人。
若甲分得8瓶 则乙分得2瓶
弱甲分得7瓶 则乙分得3瓶
若甲分得6瓶 则乙分得4瓶
若甲分得5瓶 则乙分得5瓶
1.在此过程中,“守恒量”是什么?
矿泉水的总量
2.如何求出这个“守恒量”呢?
选择其中一次进行相加
思考:从上个问题中可以得出,“守恒规律”有什么样的特点?
1.守恒过程对应某一过程的各个状态
2.守恒规律对应某一种相同的物理量
3.守恒规律可以表达为形如a=a的形式
二、回到标题:“机械能守恒定律”,到底是啥守恒?
回忆:“机械能守恒“中的机械能是指什么?
小球的运动有什么规律?小球在运动过程中,h、v怎么变?
高度h 速度v
A--B 减小 增大
B--C 增大 减小
C--B 减小 增大
B--A 增大 减小
小球荡来荡去, 重复该过程 此消彼涨
根据刚刚的实验,完成下列表格:
猜想:在这个过程中,会不会也存在“守恒量”呢?如何比较?
三、验证猜想
①亏了。猪肉比牛肉便宜,换成猪肉的话,肉的总价值可能减少了。
②赚了。换到的猪肉比牛肉要多,这样能吃得更加饱。
③赚/亏了。猪肉(牛肉)比牛肉(猪肉)更好吃。
在比较时,应该将要比较的值,转化成单位相同的量来比较
脑筋急转弯:2斤牛肉,换5斤猪肉,是亏了还是赚了?
重力势能变化 动能变化
A--B 减小 增大
B--C 增大 减小
C--B 减小 增大
B--A 增大 减小
小球荡来荡去, 重复该过程 此消彼涨
探究:重力势能和动能的转化
思考:在小球摆动的过程中,重力势能和动能是否完全相互转化?
小球的机械能是否守恒?
四、猜想与验证:小球在摆动过程中的动能与重力势能没有发生完全的转化,
那么是什么原因导致损耗的?
在单摆上的小铁球旁加上塑料球、泡沫球,让它们从同一高度释放,
观察各种小球的运动情况,分析其受力及其做功情况。
材料 泡沫球 塑料球 钢球
受力情况 重力/拉力/很大阻力 重力/拉力/较小阻力 重力/拉力/很小阻力
做功情况 重力做功/阻力做功很多 重力做功/阻力做功较少 重力做功/阻力做功很少
机械能变化情况 减小得很快 减小较快 减少很慢
由此可推导出:若完全没有阻力做功(即只有重力做功),动能和重
力势能转化的过程中,总的机械能不变。
推一下它可以吗?
你能用公式证明上面的结论吗?
小球从1--2 的过程中,机械能转化情况如何?
WG=Ep1-Ep2
WG-Wf=EK2-EK1,
联立得:
Ep1-Ep2-Wf=EK2-EK1
Ep1+EK1=Ep2+EK2+Wf
E1≠E2
若Wf=0,则E1=E2
五、探究:动能与弹性势能的转化
分析:在滑块运动过程中,其动能和弹性势能的转化情况如何?
运动过程 Ep弹变化 EK变化
A--B 减小 增大
B--C 增大 减小
C--B 减小 增大
B--A 增大 减小
循环往复 此消彼涨
受哪些力 哪些力做功
滑块 重力、支持力、弹簧弹力、阻力 弹簧弹力做功、阻力做功很少
此时的机械能
守恒吗?
与上个实验一样,你能用公式表示出系统的机械能变化情况吗?
WG=Ep1-Ep2
WG-Wf=EK2-EK1,
联立得:
Ep1-Ep2-Wf=EK2-EK1
Ep1+EK1=Ep2+EK2+Wf
E1≠E2
W弹=Ep弹1-Ep弹2
W弹-Wf=EK2-EK1,
联立得:
Ep弹1-Ep弹2-Wf=EK2-EK1
Ep弹1+EK1=Ep弹2+EK2+Wf
E1≠E2
若Wf=0,则机械能守恒。
结论:若只有弹簧弹力做功,动能和弹性势能转化过程中,
总的机械能守恒。
探究:动能和重力势能、弹性势能的转化规律
W弹=Ep弹1-Ep弹2
W弹-Wf=EK2-EK1,
联立得:
Ep弹1-Ep弹2-Wf=EK2-EK1
Ep弹1+EK1=Ep弹2+EK2+Wf
E1≠E2
W弹=Ep弹1-Ep弹2
WG=Ep1-Ep2
WG+W弹-Wf=EK2-EK1,
联立得:
Ep1-Ep2+Ep弹1-Ep弹2-Wf=EK2-EK1
Ep1+Ep弹1+EK1=Ep弹2+EK2+Ep2+Wf
E1≠E2
若Wf=0,则机械能守恒
注意! 机械能守恒,指的是重物的机械能守恒吗?
指重物、地球、弹簧所组成的系统机械能守恒
课堂小结:机械能守恒定律
机械能守恒定律
1.内容:在只有重力或者弹力做功的系统内,动能与势能可以相互转化,而总的机械能保持不变。
2.机械能为守恒量,即机械能保持不变。
3.表达式:E1=E2,Ep1+EK1=Ep2+EK2
生活中的守恒
1.守恒过程对应某一过程的各个状态
2.守恒规律对应某一种相同的物理量
3.守恒规律可以表达为形如a=a的形式
谢 谢!
