6.1.3向量的减法 课件(共45张PPT)-2024-2025学年高一下学期数学人教B版(2019)必修第二册
文档属性
| 名称 | 6.1.3向量的减法 课件(共45张PPT)-2024-2025学年高一下学期数学人教B版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 49.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 06:45:56 | ||
图片预览











文档简介
(共45张PPT)
人教B版(2019)必修第二册
6.1.3向量的减法
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
理解相反向量的含义,能用相反向量说出向量减法的意义
01
掌握向量减法的运算及其几何意义,能熟练地进行向量的加减运算
02
能将向量的减法运算转化为向量的加法运算
03
探索新知
part 02
探索新知
02
尝试与发现
知识点1 向量减法的三角形法则
问题 已知向量是向量与向量的和,如图所示,你能作出表示向量的有向线段吗?
由向量加法的三角形法则可知,
A
B
D
x
向量实际上就是向量.
探索新知
02
抽象概念
知识点1 向量减法的三角形法则
向量的差:
一般地,平面上任意给定两个向量 ,,如果向量 能满足 + = ,则称 为向量 与 的差,并记作 = – ;
在平面内任取一点O,作=,=,作出向量,则,因此向量就是向量 与 的差 (差向量),即:
探索新知
02
尝试与发现
知识点1 向量减法的三角形法则
向量减法的三角形法则:
当 与 不共线时:求 – 可用下图表示,此时向量, , – 正好能构成一个三角形,因此这种求两向量差的作图方法称为向量减法的三角形法则;
a
b
a
b
探索新知
02
尝试与发现
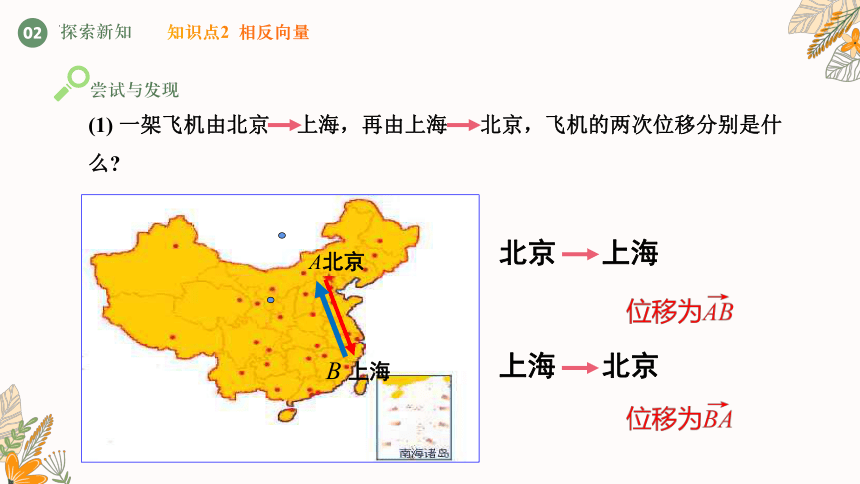
知识点2 相反向量
(1) 一架飞机由北京 上海,再由上海 北京,飞机的两次位移分别是什么
B
A
上海 北京
B 上海
A北京
北京 上海
探索新知
02
尝试与发现
知识点2 相反向量
(2)物理学中的作用力与反作用力有什么联系与区别?
大小相等
方向相反
探索新知
02
尝试与发现
知识点2 相反向量
(3)结合以上特点,你能否在正六边形中,找到也具有这种特点的两个向量?
A
O
D
C
B
E
F
探索新知
02
尝试与发现
知识点2 相反向量
思考:你还能回想起实数的相反数是怎样定义的吗?
实数a的相反数记作-a。
给定一个向量,我们把与这个向量方向相反,大小相等的向量,叫做的相反向量,记作.
如何类比定义相反向量呢?
探索新知
02
尝试与发现
知识点2 相反向量
给定一个向量,我们把与这个向量方向相反,大小相等的向量,叫做的相反向量,记作.
性质:
(1);
(2)零向量的始点与终点相同,即 = ;
(3);
(4)如果是 a,b 互为相反的向量,那么 .
探索新知
02
尝试与发现
知识点2 相反向量
类比数的减法运算,向量的减法可以转化为向量的加法来进行,即:减去一个向量相当于加上这个向量的相反向量.
+ ()
a
b
– b
a + (– b)
a – b
探索新知
02
尝试与发现
知识点2 相反向量
已知向量a和b,你能尝试通过作图得到a-b吗?
O
A
B
D
C
探索新知
02
尝试与发现
知识点2 相反向量
ab
b
b
a+(-b)
1.两个向量相减,则表示两个向量起点的字母必须相同.
2.差向量是减向量的终点指向被减向量的终点.
注意
a
向量减法的几何意义是什么
探索新知
02
尝试与发现
知识点2 相反向量
a
O
A
B
b
.
向量减法的三角形法则
共起点,连终点,指向被减向量.
注意
a-b可以表示为从向量b的终点指向向量a的终点,这就是向量减法的几何意义
向量减法的几何意义是什么
探索新知
02
尝试与发现
知识点2 相反向量
如果从a的终点到b的终点作向量,那么所得向量是什么?
向量b的方向指向向量的终点,向量b的方向指向向量b的终点,即:两个向量差向量的方向指向“被减向量”.
b
b
b
b
b
一句话总结向量的减法,即“共起点,连终点,方向指向被减向量”.
探索新知
02
尝试与发现
知识点2 相反向量
如果向量a∥b( a 、 b均不为零向量),怎样作出b呢?
a
b
b
ab
O
A
B
O
A
B
探索新知
02
例1 已知平行四边形 ABCD 中, = , = ,用 , 分别表示向量 ,.
解:如图,由向量的加法的平行四边形法则可知:
= + = + ,
按照减法的定义可知: = - = - .
a
b
A
B
C
D
探索新知
02
例2 已知 || = 1,|| = 2,求 | – | 的取值范围.
解:当 与 不共线时:由向量减法的三角法则可知,
||,||,| - | 正好是一个三角形的三条边,从而
< < || + ||,
a
b
–
因此 1 < < 3;
当 与 共线时:如果 与 方向相同,有 = =1;
如果 与 方向相反,有 = || + || = 3;
综上所述,1 ≤ | - | ≤ 3.
题型突破
part 03
题型突破
03
题型1 向量的减法运算
②用b,c表示.
例1. (1)如图所示,
①用a,b表示;
= - =--=-a-b.
=-=-(+ )=-b-c.
题型突破
03
题型1 向量的减法运算
② (-)-(-);
(2)化简下列各向量的表达式:
① +-;
③ (++)-(--).
+-= -
=
(-)-(-) = (+)-(+)
=-
=
(+ +)-(--)
=-
=
= (+) -(-)
题型突破
03
题型1 向量的减法运算
② (-)-(-);
一题多法
原式=--+
=(+)-(+)
= -
=0
法一:加法法则
法二:减法法则(利用相反向量)
原式=--+
=( -)+(-)
=+
=0
题型突破
03
题型1 向量的减法运算
② (-)-(-);
一题多法
原式=--+
=(-)-(-)-(-) +(-)
=--+-++-
=0
法三:减法法则(创造同一起点)
题型突破
03
解题通法
向量减法运算的常用方法
(1)可以通过相反向量,把向量减法的运算转化为加法运算
(2)运用向量减法的三角形法则,此时要注意两个向量要有共同的起点
(3)引入点O,逆用向量减法的三角形法则,将各向量起点统一
题型1 向量的减法运算
题型突破
03
题型2 向量减法的几何意义及简单应用
例2. (1)如图所示,四边形ABCD中,若=a, =b, =c,则=( )
A.a-b+c B.b-(a+c)
C.a+b+c D.b-a+c
=
=
= a+c-b
A
题型突破
03
题型2 向量减法的几何意义及简单应用
(2)如图所示,已知向量a,b,c不共线,求作向量a+b-c.
则=a+b-c.
法一:几何意义法
在平面内任取一点O,作=a, =b,
O
A
a
B
b
则=a+b,
再作=c,
a+b
C
c
a+b-c
题型突破
03
题型2 向量减法的几何意义及简单应用
(2)如图所示,已知向量a,b,c不共线,求作向量a+b-c.
法二:定义法
再作=-c,连接OC,则=a+b-c.
在平面内任取一点O,
作=a, =b,则=a+b,
O
A
a
B
b
a+b
-c
C
a+b-c
题型突破
03
解题通法
求作两个向量的差向量的两种思路
(1)可以转化为向量的加法来进行,如a-b,可以先作-b,然后作a+(-b)即可.
(2)可以直接用向量减法的三角形法则,即把两向量的起点重合,则差向量为连接两个向量的终点,指向被减向量的终点的向量.
题型2 向量减法的几何意义及简单应用
题型突破
03
题型3 求模的范围
例3. 已知||=6,||=9,求|-|的取值范围.
∵|||-|||≤|-|≤||+||,且||=9,||=6,
∴3≤|-|≤15.
当与同向时,| - |=3;
当与反向时,| - |=15.
∴| - |的取值范围为[3,15].
题型突破
03
题型3 求模的范围
变式1 将本例的条件改为“||=8,||=5”,求||的取值范围.
因为= - ,||=8,||=5,
|||-|||≤|- |≤||+||,
所以3≤||≤13,
当与同向时,||=3;
当与反向时,||=13.
所以||的取值范围是[3,13].
题型突破
03
题型3 求模的范围
变式2 在本例条件不变的条件下,求:|+|的取值范围.
由|||-|||≤|+|≤||+||,
∵||=6,||=9,
∴3≤|+|≤15.
当与同向时,| + |=15;
当与反向时,| + |=3.
题型突破
03
题型3 求模的范围
变式3 本例中条件“||=9”改为“||=9”,求||的取值范围.
= - ,又||=||,
由|||-|||≤|-|≤||+||,
∴3≤||≤15.
题型突破
03
解题通法
1.用向量法解决平面几何问题的步骤
(1)将平面几何问题中的量抽象成向量.
(2)化归为向量问题,进行向量运算.
(3)将向量问题还原为平面几何问题
题型3 求模的范围
2.用向量法证明四边形为平行四边形的方法和解题关键
(1)利用向量证明线段平行且相等,从而证明四边形为平行四边形,只需证明对应有向线段所表示的向量相等即可.
(2)根据图形灵活应用向量的运算法则,找到向量之间的关系是解决此类问题的关键.
当堂检测
part 04
当堂检测
04
B
当堂检测
04
①
当堂检测
04
当堂检测
04
12
0
当堂检测
04
当堂检测
04
当堂检测
04
谢谢观看
learn to report
人教B版(2019)必修第二册
6.1.3向量的减法
学习目标
Learning Objectives
探索新知
Explore new knowledge
题型突破
Breakthrough in question types
当堂检测
Classroom test
学习目录
parent conference directory
壹
叁
贰
肆
学习目标
part 01
学习目标
01
理解相反向量的含义,能用相反向量说出向量减法的意义
01
掌握向量减法的运算及其几何意义,能熟练地进行向量的加减运算
02
能将向量的减法运算转化为向量的加法运算
03
探索新知
part 02
探索新知
02
尝试与发现
知识点1 向量减法的三角形法则
问题 已知向量是向量与向量的和,如图所示,你能作出表示向量的有向线段吗?
由向量加法的三角形法则可知,
A
B
D
x
向量实际上就是向量.
探索新知
02
抽象概念
知识点1 向量减法的三角形法则
向量的差:
一般地,平面上任意给定两个向量 ,,如果向量 能满足 + = ,则称 为向量 与 的差,并记作 = – ;
在平面内任取一点O,作=,=,作出向量,则,因此向量就是向量 与 的差 (差向量),即:
探索新知
02
尝试与发现
知识点1 向量减法的三角形法则
向量减法的三角形法则:
当 与 不共线时:求 – 可用下图表示,此时向量, , – 正好能构成一个三角形,因此这种求两向量差的作图方法称为向量减法的三角形法则;
a
b
a
b
探索新知
02
尝试与发现
知识点2 相反向量
(1) 一架飞机由北京 上海,再由上海 北京,飞机的两次位移分别是什么
B
A
上海 北京
B 上海
A北京
北京 上海
探索新知
02
尝试与发现
知识点2 相反向量
(2)物理学中的作用力与反作用力有什么联系与区别?
大小相等
方向相反
探索新知
02
尝试与发现
知识点2 相反向量
(3)结合以上特点,你能否在正六边形中,找到也具有这种特点的两个向量?
A
O
D
C
B
E
F
探索新知
02
尝试与发现
知识点2 相反向量
思考:你还能回想起实数的相反数是怎样定义的吗?
实数a的相反数记作-a。
给定一个向量,我们把与这个向量方向相反,大小相等的向量,叫做的相反向量,记作.
如何类比定义相反向量呢?
探索新知
02
尝试与发现
知识点2 相反向量
给定一个向量,我们把与这个向量方向相反,大小相等的向量,叫做的相反向量,记作.
性质:
(1);
(2)零向量的始点与终点相同,即 = ;
(3);
(4)如果是 a,b 互为相反的向量,那么 .
探索新知
02
尝试与发现
知识点2 相反向量
类比数的减法运算,向量的减法可以转化为向量的加法来进行,即:减去一个向量相当于加上这个向量的相反向量.
+ ()
a
b
– b
a + (– b)
a – b
探索新知
02
尝试与发现
知识点2 相反向量
已知向量a和b,你能尝试通过作图得到a-b吗?
O
A
B
D
C
探索新知
02
尝试与发现
知识点2 相反向量
ab
b
b
a+(-b)
1.两个向量相减,则表示两个向量起点的字母必须相同.
2.差向量是减向量的终点指向被减向量的终点.
注意
a
向量减法的几何意义是什么
探索新知
02
尝试与发现
知识点2 相反向量
a
O
A
B
b
.
向量减法的三角形法则
共起点,连终点,指向被减向量.
注意
a-b可以表示为从向量b的终点指向向量a的终点,这就是向量减法的几何意义
向量减法的几何意义是什么
探索新知
02
尝试与发现
知识点2 相反向量
如果从a的终点到b的终点作向量,那么所得向量是什么?
向量b的方向指向向量的终点,向量b的方向指向向量b的终点,即:两个向量差向量的方向指向“被减向量”.
b
b
b
b
b
一句话总结向量的减法,即“共起点,连终点,方向指向被减向量”.
探索新知
02
尝试与发现
知识点2 相反向量
如果向量a∥b( a 、 b均不为零向量),怎样作出b呢?
a
b
b
ab
O
A
B
O
A
B
探索新知
02
例1 已知平行四边形 ABCD 中, = , = ,用 , 分别表示向量 ,.
解:如图,由向量的加法的平行四边形法则可知:
= + = + ,
按照减法的定义可知: = - = - .
a
b
A
B
C
D
探索新知
02
例2 已知 || = 1,|| = 2,求 | – | 的取值范围.
解:当 与 不共线时:由向量减法的三角法则可知,
||,||,| - | 正好是一个三角形的三条边,从而
< < || + ||,
a
b
–
因此 1 < < 3;
当 与 共线时:如果 与 方向相同,有 = =1;
如果 与 方向相反,有 = || + || = 3;
综上所述,1 ≤ | - | ≤ 3.
题型突破
part 03
题型突破
03
题型1 向量的减法运算
②用b,c表示.
例1. (1)如图所示,
①用a,b表示;
= - =--=-a-b.
=-=-(+ )=-b-c.
题型突破
03
题型1 向量的减法运算
② (-)-(-);
(2)化简下列各向量的表达式:
① +-;
③ (++)-(--).
+-= -
=
(-)-(-) = (+)-(+)
=-
=
(+ +)-(--)
=-
=
= (+) -(-)
题型突破
03
题型1 向量的减法运算
② (-)-(-);
一题多法
原式=--+
=(+)-(+)
= -
=0
法一:加法法则
法二:减法法则(利用相反向量)
原式=--+
=( -)+(-)
=+
=0
题型突破
03
题型1 向量的减法运算
② (-)-(-);
一题多法
原式=--+
=(-)-(-)-(-) +(-)
=--+-++-
=0
法三:减法法则(创造同一起点)
题型突破
03
解题通法
向量减法运算的常用方法
(1)可以通过相反向量,把向量减法的运算转化为加法运算
(2)运用向量减法的三角形法则,此时要注意两个向量要有共同的起点
(3)引入点O,逆用向量减法的三角形法则,将各向量起点统一
题型1 向量的减法运算
题型突破
03
题型2 向量减法的几何意义及简单应用
例2. (1)如图所示,四边形ABCD中,若=a, =b, =c,则=( )
A.a-b+c B.b-(a+c)
C.a+b+c D.b-a+c
=
=
= a+c-b
A
题型突破
03
题型2 向量减法的几何意义及简单应用
(2)如图所示,已知向量a,b,c不共线,求作向量a+b-c.
则=a+b-c.
法一:几何意义法
在平面内任取一点O,作=a, =b,
O
A
a
B
b
则=a+b,
再作=c,
a+b
C
c
a+b-c
题型突破
03
题型2 向量减法的几何意义及简单应用
(2)如图所示,已知向量a,b,c不共线,求作向量a+b-c.
法二:定义法
再作=-c,连接OC,则=a+b-c.
在平面内任取一点O,
作=a, =b,则=a+b,
O
A
a
B
b
a+b
-c
C
a+b-c
题型突破
03
解题通法
求作两个向量的差向量的两种思路
(1)可以转化为向量的加法来进行,如a-b,可以先作-b,然后作a+(-b)即可.
(2)可以直接用向量减法的三角形法则,即把两向量的起点重合,则差向量为连接两个向量的终点,指向被减向量的终点的向量.
题型2 向量减法的几何意义及简单应用
题型突破
03
题型3 求模的范围
例3. 已知||=6,||=9,求|-|的取值范围.
∵|||-|||≤|-|≤||+||,且||=9,||=6,
∴3≤|-|≤15.
当与同向时,| - |=3;
当与反向时,| - |=15.
∴| - |的取值范围为[3,15].
题型突破
03
题型3 求模的范围
变式1 将本例的条件改为“||=8,||=5”,求||的取值范围.
因为= - ,||=8,||=5,
|||-|||≤|- |≤||+||,
所以3≤||≤13,
当与同向时,||=3;
当与反向时,||=13.
所以||的取值范围是[3,13].
题型突破
03
题型3 求模的范围
变式2 在本例条件不变的条件下,求:|+|的取值范围.
由|||-|||≤|+|≤||+||,
∵||=6,||=9,
∴3≤|+|≤15.
当与同向时,| + |=15;
当与反向时,| + |=3.
题型突破
03
题型3 求模的范围
变式3 本例中条件“||=9”改为“||=9”,求||的取值范围.
= - ,又||=||,
由|||-|||≤|-|≤||+||,
∴3≤||≤15.
题型突破
03
解题通法
1.用向量法解决平面几何问题的步骤
(1)将平面几何问题中的量抽象成向量.
(2)化归为向量问题,进行向量运算.
(3)将向量问题还原为平面几何问题
题型3 求模的范围
2.用向量法证明四边形为平行四边形的方法和解题关键
(1)利用向量证明线段平行且相等,从而证明四边形为平行四边形,只需证明对应有向线段所表示的向量相等即可.
(2)根据图形灵活应用向量的运算法则,找到向量之间的关系是解决此类问题的关键.
当堂检测
part 04
当堂检测
04
B
当堂检测
04
①
当堂检测
04
当堂检测
04
12
0
当堂检测
04
当堂检测
04
当堂检测
04
谢谢观看
learn to report
