北师大版六年级上册数学第一单元 圆的阴影部分面积求解(课件)(共29张PPT)
文档属性
| 名称 | 北师大版六年级上册数学第一单元 圆的阴影部分面积求解(课件)(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 07:54:47 | ||
图片预览



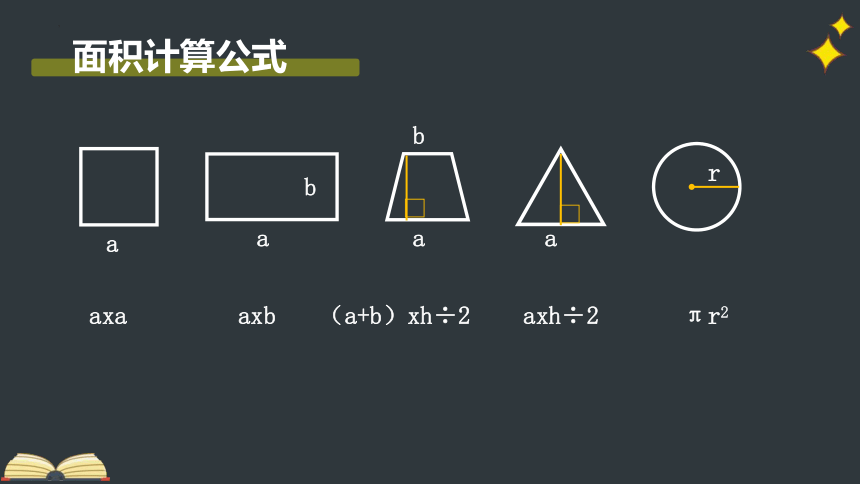


文档简介
(共29张PPT)
圆的阴影部分面积
方法总结专项
2.和差法
3.平移法
5.辅助线法
1.直接求法
7.平移法
6.割补法
8.旋转法
9.对称添补法
10.重叠法
01
直接求法
面积计算公式
a
a
b
b
a
a
r
axa
axb
(a+b)xh÷2
axh÷2
πr2
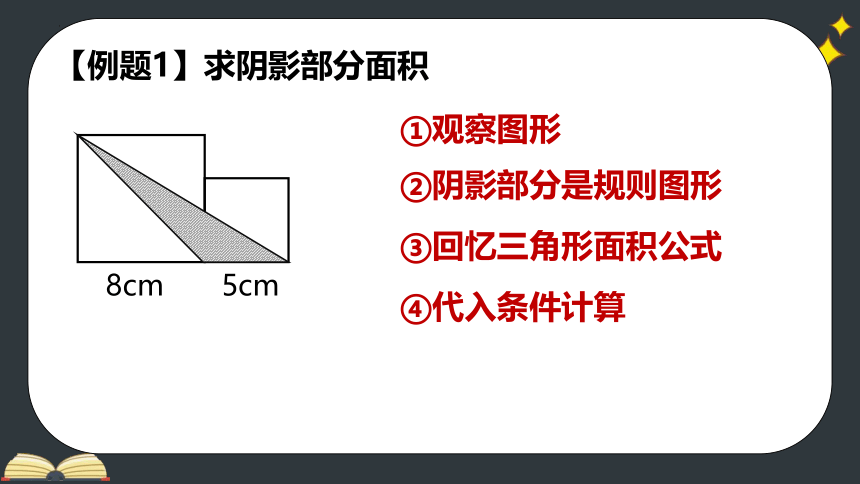
【例题1】求阴影部分面积
①观察图形
②阴影部分是规则图形
③回忆三角形面积公式
④代入条件计算
8cm
5cm
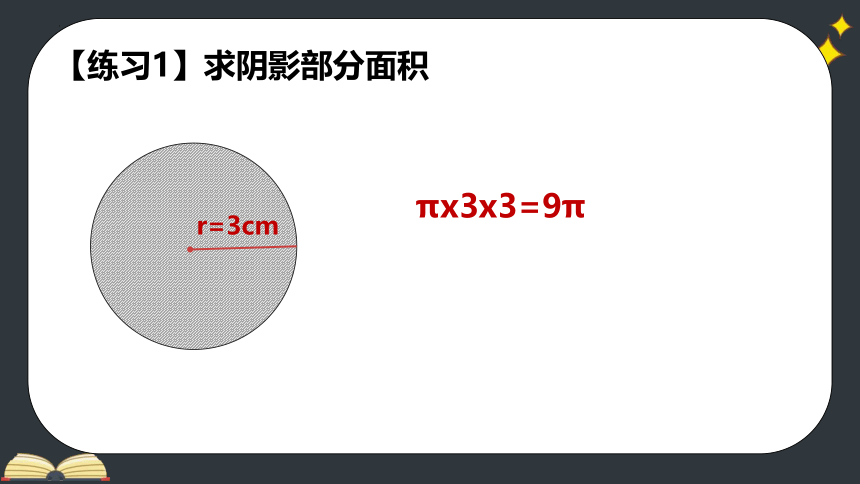
【练习1】求阴影部分面积
πx3x3=9π
r=3cm
02
和差法
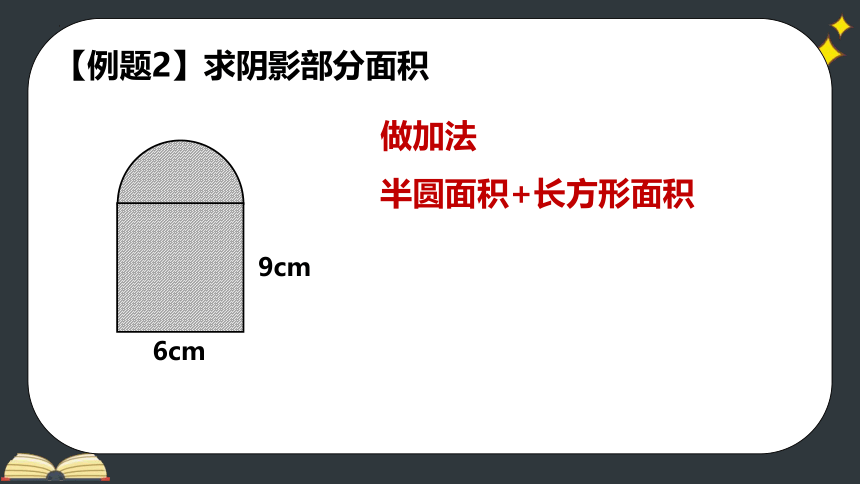
【例题2】求阴影部分面积
做加法
6cm
9cm
半圆面积+长方形面积
【练习1】求阴影部分面积
做减法
大圆面积-小圆面积
R=8cm
r=4cm
(8x8-4x4)π
=48π
【练习2】求阴影部分面积
做加法
一个圆+一个正方形
4x4xπ+4x4
=16π+16
【练习3】求阴影部分面积
正方形-四分之一圆
8x8-8x8π÷4
=64-16π
【练习4】求阴影部分面积
正方形-圆
=10x10-5x5π
=100-25π
思考
4cm
【特殊情况】容斥原理
【特殊情况】容斥原理
4cm
【特殊情况】容斥原理
①
②
③
①标序号
②找规则图形
① ②
② ③
②
① ② ③
4cm
【特殊情况】容斥原理
03
割补法
【例题3】求阴影部分面积
割补法
把不规则图形,通过割补的方式拼成规则的
【例题3】求阴影部分面积
割补法
6cm
求长方形面积
6x10=60平方厘米
【练习1】求阴影部分面积
割补法
【练习1】求阴影部分面积
割补法
半圆的面积
πx5x5=25π平方厘米
【练习2】求阴影部分面积
6cm
【练习2】求阴影部分面积
6cm
割补法
【练习2】求阴影部分面积
割补法
6cm
求三角形的面积
6x6÷2=18平方厘米
04
整体代入
【例题4】半圆的面积为12.56,求阴影部分面积。
因为:S阴影=rxr÷2
已知:S半圆=rxrxπ÷2=12.56
rxr=12.56x2÷3.14=8
所以:S阴影=rxr÷2
=8÷2
=4
r
【练习1】半圆的面积为12.56,求阴影部分面积。
因为:S阴影=rxr÷2
已知:S半圆=rxrxπ÷2=12.56
rxr=12.56x2÷3.14=8
所以:S阴影=rxr÷2
=8÷2
=4
r
【练习1】已知阴影部分面积为75平方厘米,求圆环面积是多少。
因为:S圆环=(R2-r2)xπ
又因为:S阴影=S大正方形-S小正方形
=R2-r2
=75平方厘米
所以:S圆环=75xπ
r
R
总结笔记
利用规则图形的公式直接带入。
①加法 ②减法 ③容斥原理
1.直接求法:
根据已知条件,写出算式,研究整体
2.和差法:
3.割补法:
4.整体带入:
通过“割”或“补”的方式把不规则图形,变成规则图形。
圆的阴影部分面积
方法总结专项
2.和差法
3.平移法
5.辅助线法
1.直接求法
7.平移法
6.割补法
8.旋转法
9.对称添补法
10.重叠法
01
直接求法
面积计算公式
a
a
b
b
a
a
r
axa
axb
(a+b)xh÷2
axh÷2
πr2
【例题1】求阴影部分面积
①观察图形
②阴影部分是规则图形
③回忆三角形面积公式
④代入条件计算
8cm
5cm
【练习1】求阴影部分面积
πx3x3=9π
r=3cm
02
和差法
【例题2】求阴影部分面积
做加法
6cm
9cm
半圆面积+长方形面积
【练习1】求阴影部分面积
做减法
大圆面积-小圆面积
R=8cm
r=4cm
(8x8-4x4)π
=48π
【练习2】求阴影部分面积
做加法
一个圆+一个正方形
4x4xπ+4x4
=16π+16
【练习3】求阴影部分面积
正方形-四分之一圆
8x8-8x8π÷4
=64-16π
【练习4】求阴影部分面积
正方形-圆
=10x10-5x5π
=100-25π
思考
4cm
【特殊情况】容斥原理
【特殊情况】容斥原理
4cm
【特殊情况】容斥原理
①
②
③
①标序号
②找规则图形
① ②
② ③
②
① ② ③
4cm
【特殊情况】容斥原理
03
割补法
【例题3】求阴影部分面积
割补法
把不规则图形,通过割补的方式拼成规则的
【例题3】求阴影部分面积
割补法
6cm
求长方形面积
6x10=60平方厘米
【练习1】求阴影部分面积
割补法
【练习1】求阴影部分面积
割补法
半圆的面积
πx5x5=25π平方厘米
【练习2】求阴影部分面积
6cm
【练习2】求阴影部分面积
6cm
割补法
【练习2】求阴影部分面积
割补法
6cm
求三角形的面积
6x6÷2=18平方厘米
04
整体代入
【例题4】半圆的面积为12.56,求阴影部分面积。
因为:S阴影=rxr÷2
已知:S半圆=rxrxπ÷2=12.56
rxr=12.56x2÷3.14=8
所以:S阴影=rxr÷2
=8÷2
=4
r
【练习1】半圆的面积为12.56,求阴影部分面积。
因为:S阴影=rxr÷2
已知:S半圆=rxrxπ÷2=12.56
rxr=12.56x2÷3.14=8
所以:S阴影=rxr÷2
=8÷2
=4
r
【练习1】已知阴影部分面积为75平方厘米,求圆环面积是多少。
因为:S圆环=(R2-r2)xπ
又因为:S阴影=S大正方形-S小正方形
=R2-r2
=75平方厘米
所以:S圆环=75xπ
r
R
总结笔记
利用规则图形的公式直接带入。
①加法 ②减法 ③容斥原理
1.直接求法:
根据已知条件,写出算式,研究整体
2.和差法:
3.割补法:
4.整体带入:
通过“割”或“补”的方式把不规则图形,变成规则图形。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
