五年级上册数学人教版梯形的面积课件(共20张PPT)
文档属性
| 名称 | 五年级上册数学人教版梯形的面积课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 24.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 08:15:45 | ||
图片预览






文档简介
(共20张PPT)
梯形的面积
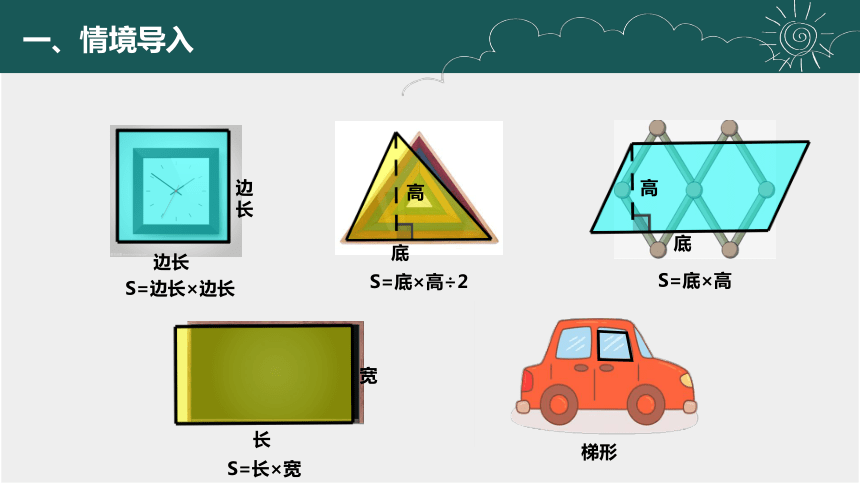
长
宽
边长
边长
S=边长×边长
底
高
S=底×高÷2
底
高
S=底×高
S=长×宽
梯形
一、情境导入
梯形的面积计算公式 = ?
你能用学过的方法推导出梯形的面积计算公式吗?
怎样求出这块梯形车窗玻璃的面积呢?
一、情境导入
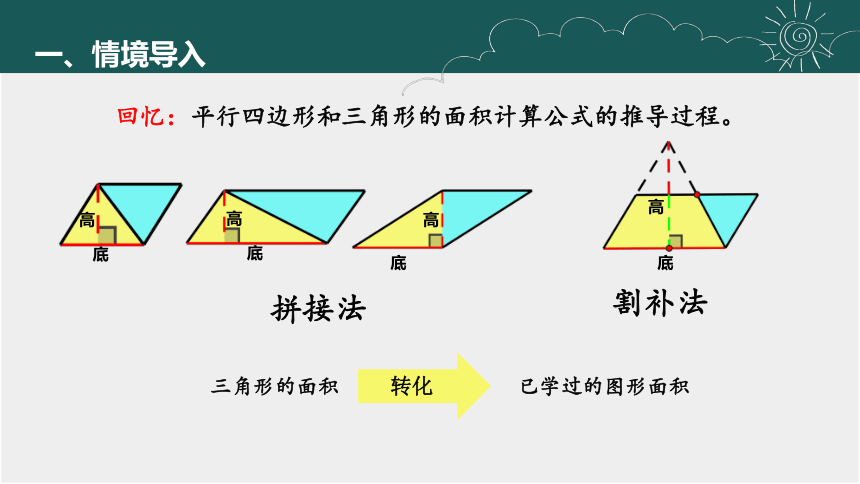
回忆:平行四边形和三角形的面积计算公式的推导过程。
拼接法
平行四边形面积
转化
已学过的图形面积
一、情境导入
回忆:平行四边形和三角形的面积计算公式的推导过程。
底
高
底
高
底
高
底
高
拼接法
割补法
三角形的面积
转化
已学过的图形面积
一、情境导入
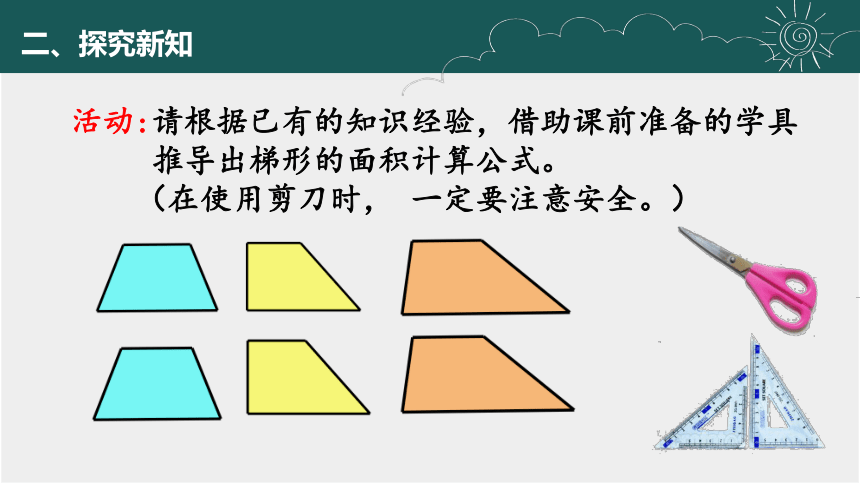
活动:请根据已有的知识经验,借助课前准备的学具
推导出梯形的面积计算公式。
(在使用剪刀时, 一定要注意安全。)
二、探究新知
小组合作要求:
试一试:将手中的梯形用你喜欢的方法转化成 我们已经学过的图形?
说一说:转化后的的图形各部分与梯形有什么关系?
探一探:怎样计算梯形的面积?
二、探究新知
任意两个完全相同的梯形可以拼成一个平行四边形
上底
上底
下底
下底
高
高
拼接法
二、探究新知
下底
上底
+
平行四边形的底
平行四边形的底
下底
上底
+
1.拼成的平行四边形的底与梯形的底有什么关系?
拼成的平行四边形的底等于梯形的上底与下底的和。
2.拼成的平行四边形的高与梯形的高有什么关系?
拼成的平行四边形的高等于梯形的高
3.每个梯形的面积与拼成的平行四边形的面积有什么关系?
每个梯形的面积等于拼成的平行四边形的面积的一半。
高
高
二、探究新知
高
高
下底
上底
下底
上底
+
+
平行四边形的底
平行四边形的底
平行四边形
的面积
底
高
×
梯形
的面积
(上底+下底)
高
×
一半
=
=
÷2
二、探究新知
分割法
①
②
上底
下底
可以把一个梯形分成两个三角形
梯形的面积=三角形①的面积+三角形②的面积
上底×高÷2
下底×高÷2
+
(上底+下底)×高÷2
梯形的面积=(上底+下底)×高÷2
高
二、探究新知
①
分割法
②
上底
下底
把一个梯形分成1个三角形和1个平行四边形。
梯形的面积=平行四边形的面积+三角形的面积
上底×高
(下底-上底)×高÷2
+
(上底+下底)×高÷2
梯形的面积=(上底+下底)×高÷2
高
二、探究新知
割补法
思考:从梯形两腰中点的连线将梯形剪开,探究如何求梯形面积
平行四边形的高=梯形的高÷2
梯形的面积=平行四边形的面积
梯形的面积=(上底+下底) ×高÷2
二、探究新知
下底
上底
高
梯形的面积=(上底+下底)×高÷2
梯形面积计算公式是什么?
上底
下底
高
a
b
h
S
=
(a+b)
×h÷2
二、探究新知
三、课堂练习
17m
计算下面梯形的面积。
15m
23m
10m
9m
18m
30m
42m
26m
(17+23)×15÷2
=40×15÷2
=300(m )
(9+18)×10÷2
=27×10÷2
=135(m )
(26+42)×30÷2
=68×30÷2
=1020(m )
三、课堂练习
例题3:我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
36 m
135 m
120 m
三、课堂练习
例题3:我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
36 m
135 m
120 m
S=(a+b)h÷2
= (36+120)×135÷2
= 156×135÷2
= 10530(平方米)
答:它的面积是 10530 平方米。
三、课堂练习
这节课你们都学会了哪些知识?
梯形的面积
梯形的面积= (上底+下底) ×高÷2
S = (a + b) h÷2
b
a
h
四、课堂小结
谢谢大家
梯形的面积
长
宽
边长
边长
S=边长×边长
底
高
S=底×高÷2
底
高
S=底×高
S=长×宽
梯形
一、情境导入
梯形的面积计算公式 = ?
你能用学过的方法推导出梯形的面积计算公式吗?
怎样求出这块梯形车窗玻璃的面积呢?
一、情境导入
回忆:平行四边形和三角形的面积计算公式的推导过程。
拼接法
平行四边形面积
转化
已学过的图形面积
一、情境导入
回忆:平行四边形和三角形的面积计算公式的推导过程。
底
高
底
高
底
高
底
高
拼接法
割补法
三角形的面积
转化
已学过的图形面积
一、情境导入
活动:请根据已有的知识经验,借助课前准备的学具
推导出梯形的面积计算公式。
(在使用剪刀时, 一定要注意安全。)
二、探究新知
小组合作要求:
试一试:将手中的梯形用你喜欢的方法转化成 我们已经学过的图形?
说一说:转化后的的图形各部分与梯形有什么关系?
探一探:怎样计算梯形的面积?
二、探究新知
任意两个完全相同的梯形可以拼成一个平行四边形
上底
上底
下底
下底
高
高
拼接法
二、探究新知
下底
上底
+
平行四边形的底
平行四边形的底
下底
上底
+
1.拼成的平行四边形的底与梯形的底有什么关系?
拼成的平行四边形的底等于梯形的上底与下底的和。
2.拼成的平行四边形的高与梯形的高有什么关系?
拼成的平行四边形的高等于梯形的高
3.每个梯形的面积与拼成的平行四边形的面积有什么关系?
每个梯形的面积等于拼成的平行四边形的面积的一半。
高
高
二、探究新知
高
高
下底
上底
下底
上底
+
+
平行四边形的底
平行四边形的底
平行四边形
的面积
底
高
×
梯形
的面积
(上底+下底)
高
×
一半
=
=
÷2
二、探究新知
分割法
①
②
上底
下底
可以把一个梯形分成两个三角形
梯形的面积=三角形①的面积+三角形②的面积
上底×高÷2
下底×高÷2
+
(上底+下底)×高÷2
梯形的面积=(上底+下底)×高÷2
高
二、探究新知
①
分割法
②
上底
下底
把一个梯形分成1个三角形和1个平行四边形。
梯形的面积=平行四边形的面积+三角形的面积
上底×高
(下底-上底)×高÷2
+
(上底+下底)×高÷2
梯形的面积=(上底+下底)×高÷2
高
二、探究新知
割补法
思考:从梯形两腰中点的连线将梯形剪开,探究如何求梯形面积
平行四边形的高=梯形的高÷2
梯形的面积=平行四边形的面积
梯形的面积=(上底+下底) ×高÷2
二、探究新知
下底
上底
高
梯形的面积=(上底+下底)×高÷2
梯形面积计算公式是什么?
上底
下底
高
a
b
h
S
=
(a+b)
×h÷2
二、探究新知
三、课堂练习
17m
计算下面梯形的面积。
15m
23m
10m
9m
18m
30m
42m
26m
(17+23)×15÷2
=40×15÷2
=300(m )
(9+18)×10÷2
=27×10÷2
=135(m )
(26+42)×30÷2
=68×30÷2
=1020(m )
三、课堂练习
例题3:我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
36 m
135 m
120 m
三、课堂练习
例题3:我国三峡水电站大坝的横截面的一部分是梯形(如下图),求它的面积。
36 m
135 m
120 m
S=(a+b)h÷2
= (36+120)×135÷2
= 156×135÷2
= 10530(平方米)
答:它的面积是 10530 平方米。
三、课堂练习
这节课你们都学会了哪些知识?
梯形的面积
梯形的面积= (上底+下底) ×高÷2
S = (a + b) h÷2
b
a
h
四、课堂小结
谢谢大家
