2024-2025学年河南省实验中学九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年河南省实验中学九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 235.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 15:30:48 | ||
图片预览




文档简介
2024-2025学年河南省实验中学九年级(上)开学数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”,其中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.若,则下列不等式不一定成立的是( )
A. B. C. D.
3.一个多边形的内角和是,则这个多边形的边数是( )
A. B. C. D.
4.如图所示,是一块三角形的草坪,现要在草坪上修建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A. 三条边的垂直平分线的交点
B. 三个内角的角平分线的交点
C. 三角形三条边上的高的交点
D. 三角形三条中线的交点
5.下列各式中,从左到右的变形是因式分解的是( )
A. B.
C. D.
6.关于的一元二次方程的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
7.如图,四边形是平行四边形,下列结论中错误的是( )
A. 当,是矩形 B. 当,是矩形
C. 当,是菱形 D. 当,是正方形
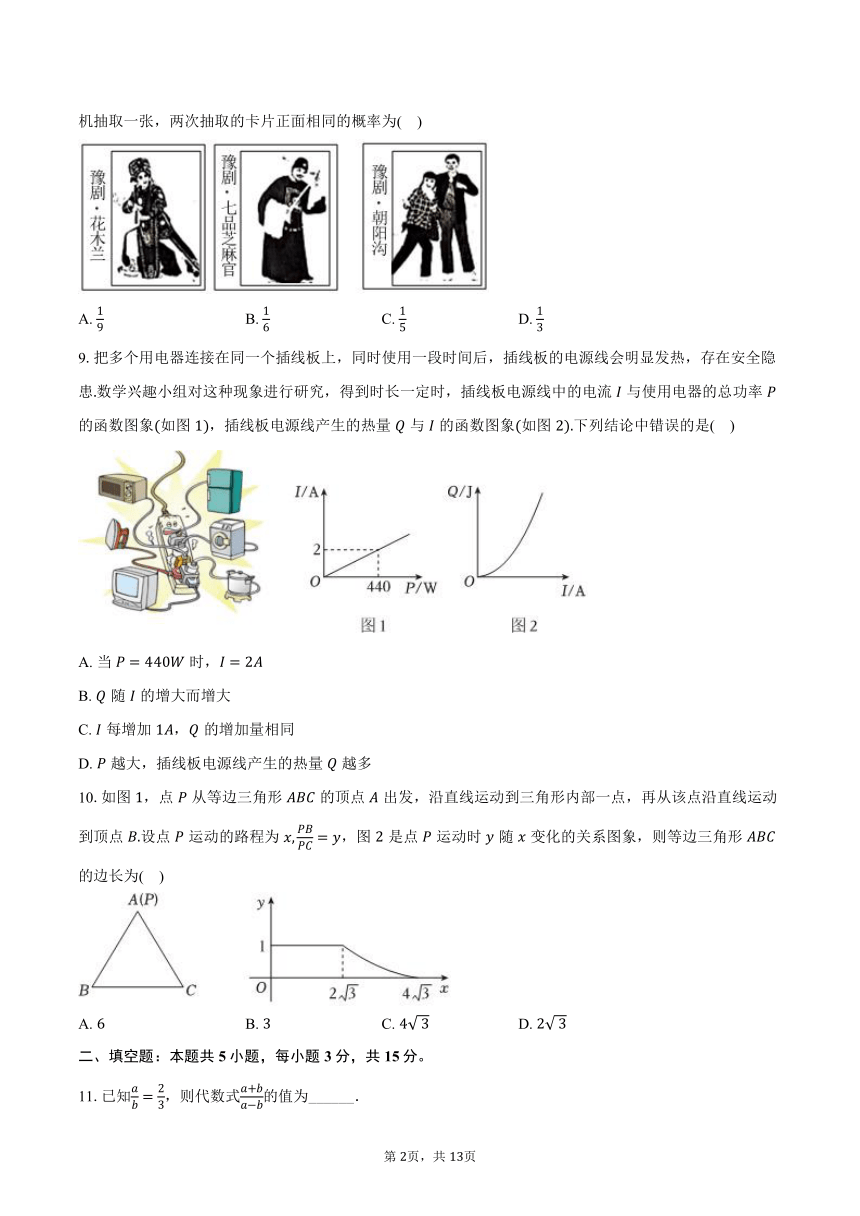
8.豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )
A. B. C. D.
9.把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流与使用电器的总功率的函数图象如图,插线板电源线产生的热量与的函数图象如图下列结论中错误的是( )
A. 当时,
B. 随的增大而增大
C. 每增加,的增加量相同
D. 越大,插线板电源线产生的热量越多
10.如图,点从等边三角形的顶点出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点设点运动的路程为,图是点运动时随变化的关系图象,则等边三角形的边长为( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
11.已知,则代数式的值为______.
12.因式分解:______.
13.如图,在平面直角坐标系中,正方形的边在轴上,点的坐标为,点在边上将沿折叠,点落在点处若点的坐标为,则点的坐标为 .
14.如图,在中,点、在上,点、分别在、上,四边形是
矩形,,是的高,,,那么的长为______.
15.如图,在中,,,,点是边上的动
点,沿所在的直线折叠,使点的对应点落在点处当与的
边平行时,线段的长为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
解方程:
;
;
;
.
17.本小题分
习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了名学生每天用于课外阅读的时间,以下是部分数据和不完整的统计图表:阅读时间在范围内的数据:,,,,,,,不完整的统计图表:
课外阅读时间 等级 人数
结合以上信息回答下列问题:
统计表中的 ______;统计图中组对应扇形的圆心角为______度;
阅读时间在范围内的数据的众数是______;根据调查结果,请你估计全校名同学课外阅读时间不少于的人数有______人;
等级学生中只有一名女生,从等级学生中选两名学生对全校学生作读书的收获和体会的报告,用列举法或树状图法求恰好选择一名男生和一名女生的概率.
18.本小题分
如图,在中,,,,点从点出发沿方向以的速度向点匀速运动,同时点从点出发沿方向以的速度向点匀速运动,当其中一个点到达终点时,另一个点也随之停止运动设点,运动的时间是过点作于点,连接,.
求证:四边形为平行四边形;
当 ______时,四边形为菱形;
当 ______时,四边形为矩形;
19.本小题分
已知关于的一元二次方程.
若该方程有两个实数根,求的最小整数值;
若方程的两个实数根为,,且,求的值.
20.本小题分
某数学兴趣小组在综合实践活动中测量古塔的高度.
【测量方案】在地面上选一点,垂直地面竖立标杆,后退到处,此时、、在一直线上;另选一点,垂直地面竖立标杆,后退到处,此时、、三点也在一直线上.
【测量数据】两次测量标杆之间的距离是为,两个标杆的高度均为,且、、、、在同一直线上请你根据以上测量数据,帮助兴趣小组求出古塔的高度.
21.本小题分
加强生活垃圾分类处理,维护公共环境和节约资源是全社会共同的责任某社区为了增强社区居民的文明意识和环境意识,营造干净、整洁、舒适的人居环境,准备购买甲、乙两种分类垃圾桶通过市场调研得知:乙种分类垃圾桶的单价比甲种分类垃圾桶的单价多元,且用元购买甲种分类垃圾桶的数量与用元购买乙种分类垃圾桶的数量相同.
求甲、乙两种分类垃圾桶的单价;
该社区计划用不超过元的资金购买甲、乙两种分类垃圾桶共个,则最少需要购买甲种分类垃圾桶多少个?
22.本小题分
如图,一次函数的图象与反比例函数的图象交于,两点.
求反比例函数的表达式;
直接写出不等式的解集;
设直线与轴交于点,若为轴上的一动点,连接,,当的面积为时,求点的坐标.
23.本小题分
问题背景:数学课上,李老师出示了如下题目:如图,在正方形中,点、分别在边、上,,求证:.
小华同学给出了如下的部分证明过程.
证明:延长到点使,连接,
四边形是正方形,
,,
在和中,
≌,
请你完成剩余的证明过程.
迁移应用:李老师在的基础上,添加了和两个条件,请求出正方形的边长.
拓展探究:如图,在边长为的正方形中,点在的延长线上,,连接交于点,动点在边上,动点在线段上点与、不重合,且,连接并延长,交射线于点,设,请直接写出的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.或
16.解:,
,
,
所以,;
,
,
,
,
,
所以,;
,
,,,
,
方程没有实数解;
,
,
,
或,
所以,.
17.,;
,;
画树状图如下:
共有种等可能的情况,其中恰好选择一名男生和一名女生的情况有种,
恰好选择一名男生和一名女生的概率为.
18.证明:由题意可知,,
,,
,
.
,,
.
又,,
,
四边形为平行四边形.
解:.
.
19.解:根据题意得,
解得,
所以的最小整数值为;
根据题意得,,
,
,
,
整理得,解得,,
,
的值为.
20.解:由题可知,,,,
,
,
∽,
,
即:,
同理∽,
,
即: ,
联立解得,,,
古塔的高度为米.
21.解:甲分类垃圾桶的单价是元,则乙分类垃圾桶的单价是元,
根据题意得,
解得,
经检验,是原方程的解,且符合题意,
.
答:甲分类垃圾桶的单价是元,乙分类垃圾桶的单价是元;
设购买甲分类垃圾桶个,则购买乙分类垃圾桶个,
依题意得:,
解得:,
为正整数,
的最小值为.
答:最少需要购买甲种分类垃圾桶个.
22.解:图象经过,
,即,
,
反比例函数表达式为:;
由图可得,不等式的解集是或;
设直线交轴于点,
在中,当时,,
,
当时,得,
解得:,
,
,
,,
,
,,,
,
解得:或,
点的坐标为或.
23.证明:如图中,
延长到点使,连接,
正方形,
,,
在和中,
,
≌,
,,
,
,
,
,
在和中,
,
≌,
,
,
.
解:由可得,
设正方形的边长是,
在中,,,,
,
解得,舍去,
正方形的边长是;
解:过点作交的延长线于,过点作于,则,
,
∽,
,
,
,
,
,
,
设,则,,
,
,
解得或舍去,
,
动点在线段上点与、不重合,,
.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”,其中既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.若,则下列不等式不一定成立的是( )
A. B. C. D.
3.一个多边形的内角和是,则这个多边形的边数是( )
A. B. C. D.
4.如图所示,是一块三角形的草坪,现要在草坪上修建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A. 三条边的垂直平分线的交点
B. 三个内角的角平分线的交点
C. 三角形三条边上的高的交点
D. 三角形三条中线的交点
5.下列各式中,从左到右的变形是因式分解的是( )
A. B.
C. D.
6.关于的一元二次方程的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
7.如图,四边形是平行四边形,下列结论中错误的是( )
A. 当,是矩形 B. 当,是矩形
C. 当,是菱形 D. 当,是正方形
8.豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )
A. B. C. D.
9.把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流与使用电器的总功率的函数图象如图,插线板电源线产生的热量与的函数图象如图下列结论中错误的是( )
A. 当时,
B. 随的增大而增大
C. 每增加,的增加量相同
D. 越大,插线板电源线产生的热量越多
10.如图,点从等边三角形的顶点出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点设点运动的路程为,图是点运动时随变化的关系图象,则等边三角形的边长为( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
11.已知,则代数式的值为______.
12.因式分解:______.
13.如图,在平面直角坐标系中,正方形的边在轴上,点的坐标为,点在边上将沿折叠,点落在点处若点的坐标为,则点的坐标为 .
14.如图,在中,点、在上,点、分别在、上,四边形是
矩形,,是的高,,,那么的长为______.
15.如图,在中,,,,点是边上的动
点,沿所在的直线折叠,使点的对应点落在点处当与的
边平行时,线段的长为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
解方程:
;
;
;
.
17.本小题分
习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了名学生每天用于课外阅读的时间,以下是部分数据和不完整的统计图表:阅读时间在范围内的数据:,,,,,,,不完整的统计图表:
课外阅读时间 等级 人数
结合以上信息回答下列问题:
统计表中的 ______;统计图中组对应扇形的圆心角为______度;
阅读时间在范围内的数据的众数是______;根据调查结果,请你估计全校名同学课外阅读时间不少于的人数有______人;
等级学生中只有一名女生,从等级学生中选两名学生对全校学生作读书的收获和体会的报告,用列举法或树状图法求恰好选择一名男生和一名女生的概率.
18.本小题分
如图,在中,,,,点从点出发沿方向以的速度向点匀速运动,同时点从点出发沿方向以的速度向点匀速运动,当其中一个点到达终点时,另一个点也随之停止运动设点,运动的时间是过点作于点,连接,.
求证:四边形为平行四边形;
当 ______时,四边形为菱形;
当 ______时,四边形为矩形;
19.本小题分
已知关于的一元二次方程.
若该方程有两个实数根,求的最小整数值;
若方程的两个实数根为,,且,求的值.
20.本小题分
某数学兴趣小组在综合实践活动中测量古塔的高度.
【测量方案】在地面上选一点,垂直地面竖立标杆,后退到处,此时、、在一直线上;另选一点,垂直地面竖立标杆,后退到处,此时、、三点也在一直线上.
【测量数据】两次测量标杆之间的距离是为,两个标杆的高度均为,且、、、、在同一直线上请你根据以上测量数据,帮助兴趣小组求出古塔的高度.
21.本小题分
加强生活垃圾分类处理,维护公共环境和节约资源是全社会共同的责任某社区为了增强社区居民的文明意识和环境意识,营造干净、整洁、舒适的人居环境,准备购买甲、乙两种分类垃圾桶通过市场调研得知:乙种分类垃圾桶的单价比甲种分类垃圾桶的单价多元,且用元购买甲种分类垃圾桶的数量与用元购买乙种分类垃圾桶的数量相同.
求甲、乙两种分类垃圾桶的单价;
该社区计划用不超过元的资金购买甲、乙两种分类垃圾桶共个,则最少需要购买甲种分类垃圾桶多少个?
22.本小题分
如图,一次函数的图象与反比例函数的图象交于,两点.
求反比例函数的表达式;
直接写出不等式的解集;
设直线与轴交于点,若为轴上的一动点,连接,,当的面积为时,求点的坐标.
23.本小题分
问题背景:数学课上,李老师出示了如下题目:如图,在正方形中,点、分别在边、上,,求证:.
小华同学给出了如下的部分证明过程.
证明:延长到点使,连接,
四边形是正方形,
,,
在和中,
≌,
请你完成剩余的证明过程.
迁移应用:李老师在的基础上,添加了和两个条件,请求出正方形的边长.
拓展探究:如图,在边长为的正方形中,点在的延长线上,,连接交于点,动点在边上,动点在线段上点与、不重合,且,连接并延长,交射线于点,设,请直接写出的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.或
16.解:,
,
,
所以,;
,
,
,
,
,
所以,;
,
,,,
,
方程没有实数解;
,
,
,
或,
所以,.
17.,;
,;
画树状图如下:
共有种等可能的情况,其中恰好选择一名男生和一名女生的情况有种,
恰好选择一名男生和一名女生的概率为.
18.证明:由题意可知,,
,,
,
.
,,
.
又,,
,
四边形为平行四边形.
解:.
.
19.解:根据题意得,
解得,
所以的最小整数值为;
根据题意得,,
,
,
,
整理得,解得,,
,
的值为.
20.解:由题可知,,,,
,
,
∽,
,
即:,
同理∽,
,
即: ,
联立解得,,,
古塔的高度为米.
21.解:甲分类垃圾桶的单价是元,则乙分类垃圾桶的单价是元,
根据题意得,
解得,
经检验,是原方程的解,且符合题意,
.
答:甲分类垃圾桶的单价是元,乙分类垃圾桶的单价是元;
设购买甲分类垃圾桶个,则购买乙分类垃圾桶个,
依题意得:,
解得:,
为正整数,
的最小值为.
答:最少需要购买甲种分类垃圾桶个.
22.解:图象经过,
,即,
,
反比例函数表达式为:;
由图可得,不等式的解集是或;
设直线交轴于点,
在中,当时,,
,
当时,得,
解得:,
,
,
,,
,
,,,
,
解得:或,
点的坐标为或.
23.证明:如图中,
延长到点使,连接,
正方形,
,,
在和中,
,
≌,
,,
,
,
,
,
在和中,
,
≌,
,
,
.
解:由可得,
设正方形的边长是,
在中,,,,
,
解得,舍去,
正方形的边长是;
解:过点作交的延长线于,过点作于,则,
,
∽,
,
,
,
,
,
,
设,则,,
,
,
解得或舍去,
,
动点在线段上点与、不重合,,
.
第1页,共1页
同课章节目录
