2024-2025学年广东省深圳市南山实验教育集团麒麟中学八年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年广东省深圳市南山实验教育集团麒麟中学八年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 139.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 15:51:02 | ||
图片预览




文档简介
2024-2025学年深圳市南山实验教育集团麒麟中学八年级(上)开学
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列运算正确的是( )
A. B.
C. D.
2.肥皂泡膜是人眼能够分辨的最薄的东西之一,它的平均厚度约为纳米,已知纳米米,那么纳米用科学记数法可表示为( )
A. B. C. D.
3.下列事件中是必然事件的是( )
A. 床前明月光 B. 大漠孤烟直 C. 手可摘星辰 D. 黄河入海流
4.根据下列已知条件,能够画出唯一的是( )
A. ,, B. ,,
C. ,, D. ,,
5.如图,平分,于点,,则点到射线的距离为( )
A. B.
C. D.
6.如图,在边长为的正方形中剪去一个边长为的小正方形,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止不含点和点,则的面积随着时间变化的函数图象大致是( )
A. B. C. D.
7.如图,将一个直角三角形纸片,沿线段折叠,使点落在处,若,则的度数为( )
A. B.
C. D.
8.将一副直角三角板按如图所示摆放,,,,则下列结论不正确的是( )
A.
B.
C.
D.
9.如图,的中线、相交于点,,垂足为,且,,,,则四边形的面积是( )
A.
B.
C.
D.
10.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形拼接而成的已知::,正方形的面积为连接,交于点,交于点,连接则图中阴影部分的面积之和为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.已知,则 ______.
12.如图,地板上每一个小正方形除颜色外都相同,向地板上随机掷一枚石子,石子落在阴影部分的概率是______.
13.长方形的周长为,其中一边为其中,面积为,则关于的关系式为______.
14.如图,直线,,分别过正方形的三个顶点,,,且相互平行,若,的距离为,,的距离为,则正方形的面积为______.
15.阅读材料:整体代值是数学中常用的方法.例如“已知,求代数式的值.”可以这样解:根据阅读材料,解决问题:若是关于的一元一次方程的解,则代数式的值是______.
三、解答题:本题共7小题,共55分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:
;
简便运算;
;
.
17.本小题分
先化简,再求值:,其中,.
18.本小题分
如图所示,已知锐角及一点.
过点作、的垂线,垂足分别是、;只作图,保留作图痕迹,不写作法
猜想与之间的关系,并证明.
19.本小题分
如图,在一条笔直的东西方向的公路上有、两地,相距米,且离公路不远处有一块山地需要开发,已知与地的距离为米,与地的距离为米,在施工过程中需要实施爆破,为了安全起见,爆破点周围半径米范围内不得进入.
山地距离公路的垂直距离为多少米?
在进行爆破时,、两地之间的公路是否有危险需要暂时封锁?若需要封锁,请求出需要封锁的公路长.
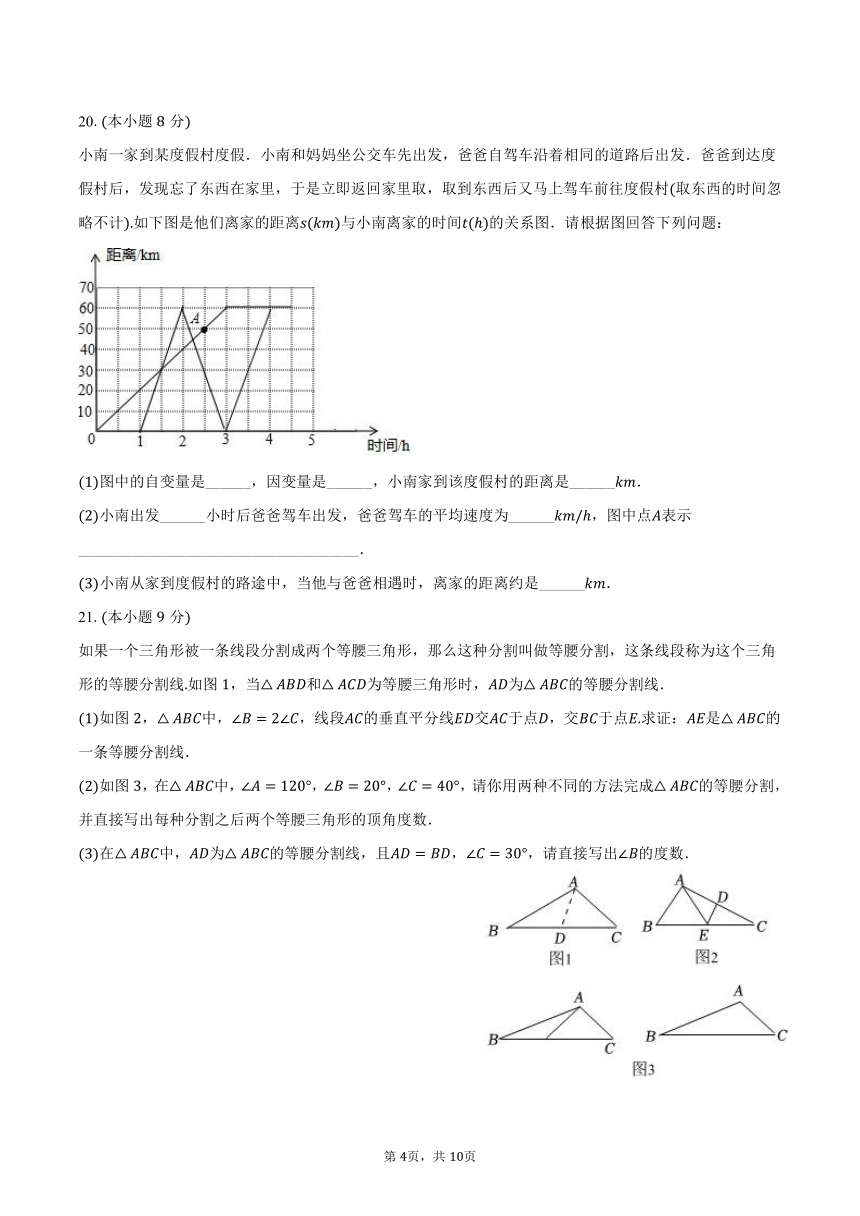
20.本小题分
小南一家到某度假村度假.小南和妈妈坐公交车先出发,爸爸自驾车沿着相同的道路后出发.爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村取东西的时间忽略不计如下图是他们离家的距离与小南离家的时间的关系图.请根据图回答下列问题:
图中的自变量是______,因变量是______,小南家到该度假村的距离是______.
小南出发______小时后爸爸驾车出发,爸爸驾车的平均速度为______,图中点表示_____________________________________.
小南从家到度假村的路途中,当他与爸爸相遇时,离家的距离约是______.
21.本小题分
如果一个三角形被一条线段分割成两个等腰三角形,那么这种分割叫做等腰分割,这条线段称为这个三角形的等腰分割线如图,当和为等腰三角形时,为的等腰分割线.
如图,中,,线段的垂直平分线交于点,交于点求证:是的一条等腰分割线.
如图,在中,,,,请你用两种不同的方法完成的等腰分割,并直接写出每种分割之后两个等腰三角形的顶角度数.
在中,为的等腰分割线,且,,请直接写出的度数.
22.本小题分
问题发现:如图,和均为等边三角形,当旋转至点,,在同一直线上,连接,易证,则
线段、之间的数量关系是______;
______;
拓展研究:如图,和均为等腰三角形,且,点,,在同一直线上,若,,求的长度;
探究发现:如图,点为等边三角形内一点,且,,,,,求的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:
;
;
;
.
17.解:
,
当,时,原式.
18.解:过点作、的垂线、如图所示;
猜想:或.
理由:左图中,在四边形中,,
.
右图中,,,
.
19.解:由题意可知,米,米,米,
,
是直角三角形,且,
如图,过点作于点,
,
米,
答:山地距离公路的垂直距离为米;
公路有危险需要暂时封锁,理由如下:
如图,过作于点,以点为圆心,米为半径画弧,交于点、,连接,,
则米,,
由可知,米,
米米,
有危险需要暂时封锁,
在中,由勾股定理得:米,
米,
即需要封锁的公路长为米.
20.解:时间;距离;;
;;小南出发小时后,离度假村的距离还有;
或.
21.证明:是的垂直平分线,
,
,是等腰三角形,
,
,
,
,
是等腰三角形,
是的一条等腰分割线;
解:如图,
解:如图,
当,时,,
如图,
当,时,,
如图,
当,时,,
综上所述:或或.
22.解:;
;
和均为等腰直角三角形,
,,,
,
在和中,
,
,,
为等腰直角三角形,
,
点,,在同一直线上,
,
,
,
;
把绕点逆时针旋转得,连接,如图所示,
则,
,,,,
是等边三角形,
,,
,
,
,
又,
即、、在同一条直线上,
,
在中,,
即的长为.
第1页,共1页
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列运算正确的是( )
A. B.
C. D.
2.肥皂泡膜是人眼能够分辨的最薄的东西之一,它的平均厚度约为纳米,已知纳米米,那么纳米用科学记数法可表示为( )
A. B. C. D.
3.下列事件中是必然事件的是( )
A. 床前明月光 B. 大漠孤烟直 C. 手可摘星辰 D. 黄河入海流
4.根据下列已知条件,能够画出唯一的是( )
A. ,, B. ,,
C. ,, D. ,,
5.如图,平分,于点,,则点到射线的距离为( )
A. B.
C. D.
6.如图,在边长为的正方形中剪去一个边长为的小正方形,动点从点出发,沿的路线绕多边形的边匀速运动到点时停止不含点和点,则的面积随着时间变化的函数图象大致是( )
A. B. C. D.
7.如图,将一个直角三角形纸片,沿线段折叠,使点落在处,若,则的度数为( )
A. B.
C. D.
8.将一副直角三角板按如图所示摆放,,,,则下列结论不正确的是( )
A.
B.
C.
D.
9.如图,的中线、相交于点,,垂足为,且,,,,则四边形的面积是( )
A.
B.
C.
D.
10.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形拼接而成的已知::,正方形的面积为连接,交于点,交于点,连接则图中阴影部分的面积之和为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.已知,则 ______.
12.如图,地板上每一个小正方形除颜色外都相同,向地板上随机掷一枚石子,石子落在阴影部分的概率是______.
13.长方形的周长为,其中一边为其中,面积为,则关于的关系式为______.
14.如图,直线,,分别过正方形的三个顶点,,,且相互平行,若,的距离为,,的距离为,则正方形的面积为______.
15.阅读材料:整体代值是数学中常用的方法.例如“已知,求代数式的值.”可以这样解:根据阅读材料,解决问题:若是关于的一元一次方程的解,则代数式的值是______.
三、解答题:本题共7小题,共55分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:
;
简便运算;
;
.
17.本小题分
先化简,再求值:,其中,.
18.本小题分
如图所示,已知锐角及一点.
过点作、的垂线,垂足分别是、;只作图,保留作图痕迹,不写作法
猜想与之间的关系,并证明.
19.本小题分
如图,在一条笔直的东西方向的公路上有、两地,相距米,且离公路不远处有一块山地需要开发,已知与地的距离为米,与地的距离为米,在施工过程中需要实施爆破,为了安全起见,爆破点周围半径米范围内不得进入.
山地距离公路的垂直距离为多少米?
在进行爆破时,、两地之间的公路是否有危险需要暂时封锁?若需要封锁,请求出需要封锁的公路长.
20.本小题分
小南一家到某度假村度假.小南和妈妈坐公交车先出发,爸爸自驾车沿着相同的道路后出发.爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村取东西的时间忽略不计如下图是他们离家的距离与小南离家的时间的关系图.请根据图回答下列问题:
图中的自变量是______,因变量是______,小南家到该度假村的距离是______.
小南出发______小时后爸爸驾车出发,爸爸驾车的平均速度为______,图中点表示_____________________________________.
小南从家到度假村的路途中,当他与爸爸相遇时,离家的距离约是______.
21.本小题分
如果一个三角形被一条线段分割成两个等腰三角形,那么这种分割叫做等腰分割,这条线段称为这个三角形的等腰分割线如图,当和为等腰三角形时,为的等腰分割线.
如图,中,,线段的垂直平分线交于点,交于点求证:是的一条等腰分割线.
如图,在中,,,,请你用两种不同的方法完成的等腰分割,并直接写出每种分割之后两个等腰三角形的顶角度数.
在中,为的等腰分割线,且,,请直接写出的度数.
22.本小题分
问题发现:如图,和均为等边三角形,当旋转至点,,在同一直线上,连接,易证,则
线段、之间的数量关系是______;
______;
拓展研究:如图,和均为等腰三角形,且,点,,在同一直线上,若,,求的长度;
探究发现:如图,点为等边三角形内一点,且,,,,,求的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:
;
;
;
.
17.解:
,
当,时,原式.
18.解:过点作、的垂线、如图所示;
猜想:或.
理由:左图中,在四边形中,,
.
右图中,,,
.
19.解:由题意可知,米,米,米,
,
是直角三角形,且,
如图,过点作于点,
,
米,
答:山地距离公路的垂直距离为米;
公路有危险需要暂时封锁,理由如下:
如图,过作于点,以点为圆心,米为半径画弧,交于点、,连接,,
则米,,
由可知,米,
米米,
有危险需要暂时封锁,
在中,由勾股定理得:米,
米,
即需要封锁的公路长为米.
20.解:时间;距离;;
;;小南出发小时后,离度假村的距离还有;
或.
21.证明:是的垂直平分线,
,
,是等腰三角形,
,
,
,
,
是等腰三角形,
是的一条等腰分割线;
解:如图,
解:如图,
当,时,,
如图,
当,时,,
如图,
当,时,,
综上所述:或或.
22.解:;
;
和均为等腰直角三角形,
,,,
,
在和中,
,
,,
为等腰直角三角形,
,
点,,在同一直线上,
,
,
,
;
把绕点逆时针旋转得,连接,如图所示,
则,
,,,,
是等边三角形,
,,
,
,
,
又,
即、、在同一条直线上,
,
在中,,
即的长为.
第1页,共1页
同课章节目录
