2024-2025学年江西省赣州中学八年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年江西省赣州中学八年级(上)开学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 105.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 00:00:00 | ||
图片预览



文档简介
2024-2025学年江西省赣州中学八年级(上)开学数学试卷
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列运算正确的是( )
A. B. C. D.
2.如果,那么下列结论错误的是( )
A. B. C. D.
3.如图的两个三角形全等,则的度数为( )
A. B. C. D.
4.如图,在中,,若沿图中的虚线截去,则( )
A.
B.
C.
D.
5.将一个含有的三角板按如图所示,摆放在一组平行线内,,则的度数为( )
A. B. C. D.
6.已知,如图,是内部的一条射线,是射线上任意点,,,下列条件中:,,,,能判定是的角平分线的有( )
A. 个
B. 个
C. 个
D. 个
二、填空题:本题共6小题,每小题3分,共18分。
7.的平方根是______,的算术平方根是______.
8.已知直线轴,且,,则的值为______.
9.已知一个样本有个数据,把它分成组,第一组到第四组的频数分别是、、、,第五组的频率是,则的值为______.
10.若的不等式组有两个整数解,则的取值范围是______.
11.个一样大小的长方形恰好可以拼成一个大的长方形,如图甲所示,若拼成如图乙所示的正方形,中间还留下一个洞,恰好是边长为厘米的小正方形设一个小长方形的长为厘米,宽为厘米,则所列二元一次方程组是______.
12.如图,,垂足为,,,射线,垂足为,动点从点出发以的速度沿射线运动,点为射线上一动点,满足,随着点运动而运动。当点运动__________秒时,与点、、为顶点的三角形全等.
三、解答题:本题共11小题,共84分。解答应写出文字说明,证明过程或演算步骤。
13.本小题分
计算:;
解方程组:.
14.本小题分
解下列不等式组,并求它的所有整数解的和.
15.本小题分
如图,矩形的一条对称轴已经作好,请用一把无刻度的直尺作出矩形的另一条对称轴.
在图中,矩形的边、上分别有、两点,且;请用一把无刻度的直尺作出矩形的一条对称轴.
16.本小题分
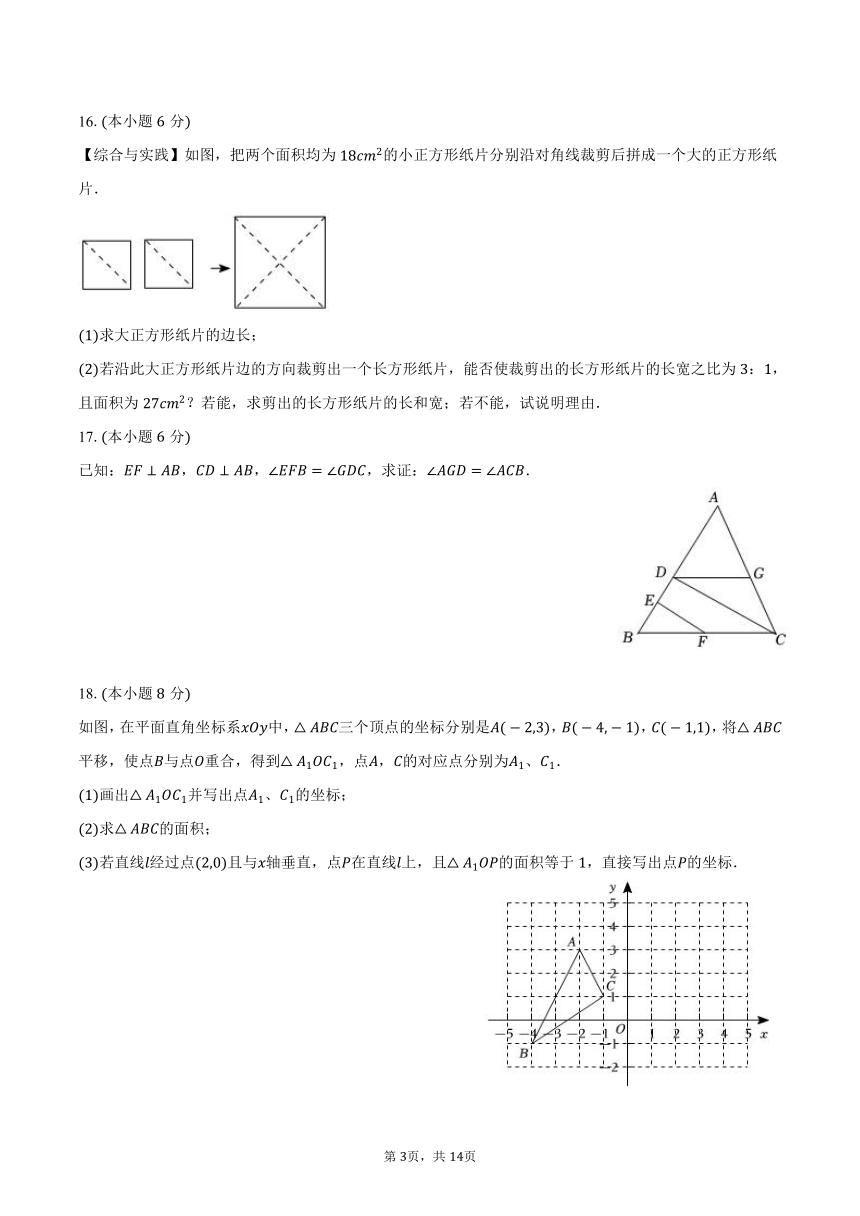
【综合与实践】如图,把两个面积均为的小正方形纸片分别沿对角线裁剪后拼成一个大的正方形纸片.
求大正方形纸片的边长;
若沿此大正方形纸片边的方向裁剪出一个长方形纸片,能否使裁剪出的长方形纸片的长宽之比为:,且面积为?若能,求剪出的长方形纸片的长和宽;若不能,试说明理由.
17.本小题分
已知:,,,求证:.
18.本小题分
如图,在平面直角坐标系中,三个顶点的坐标分别是,,,将平移,使点与点重合,得到,点,的对应点分别为、.
画出并写出点、的坐标;
求的面积;
若直线经过点且与轴垂直,点在直线上,且的面积等于,直接写出点的坐标.
19.本小题分
为鼓励居民节约用电,某市对居民用电采用阶梯电价,制定电价收费方案如表一,为了解该市某小区居民用电情况,在该小区随机抽查了户居民某月平均用电量单位:千瓦时记录数据如下:
,,,,,,,,,,,,,,.
,,,,,,,,,,,,,,.
,,,,,,,,,,,,,,
,,,,.
整理数据后得频数分布表如表二.
表一
阶梯电价方案表
档次 月平均用电量千瓦时 电价元千瓦时
第一档
第二档
第三档 大于
表二
某月平均用电量千瓦时 频数
写出 ______, ______;
若根据表二制成扇形统计图,全年月平均用电是不低于千瓦时的部分所对圆心角的度数为______;
请根据抽的数据判断,全市是否有的居民每月全部用电支出均可用第一档标准计费.
20.本小题分
如图,在中,于,分别交、于、两点,且,求证:.
21.本小题分
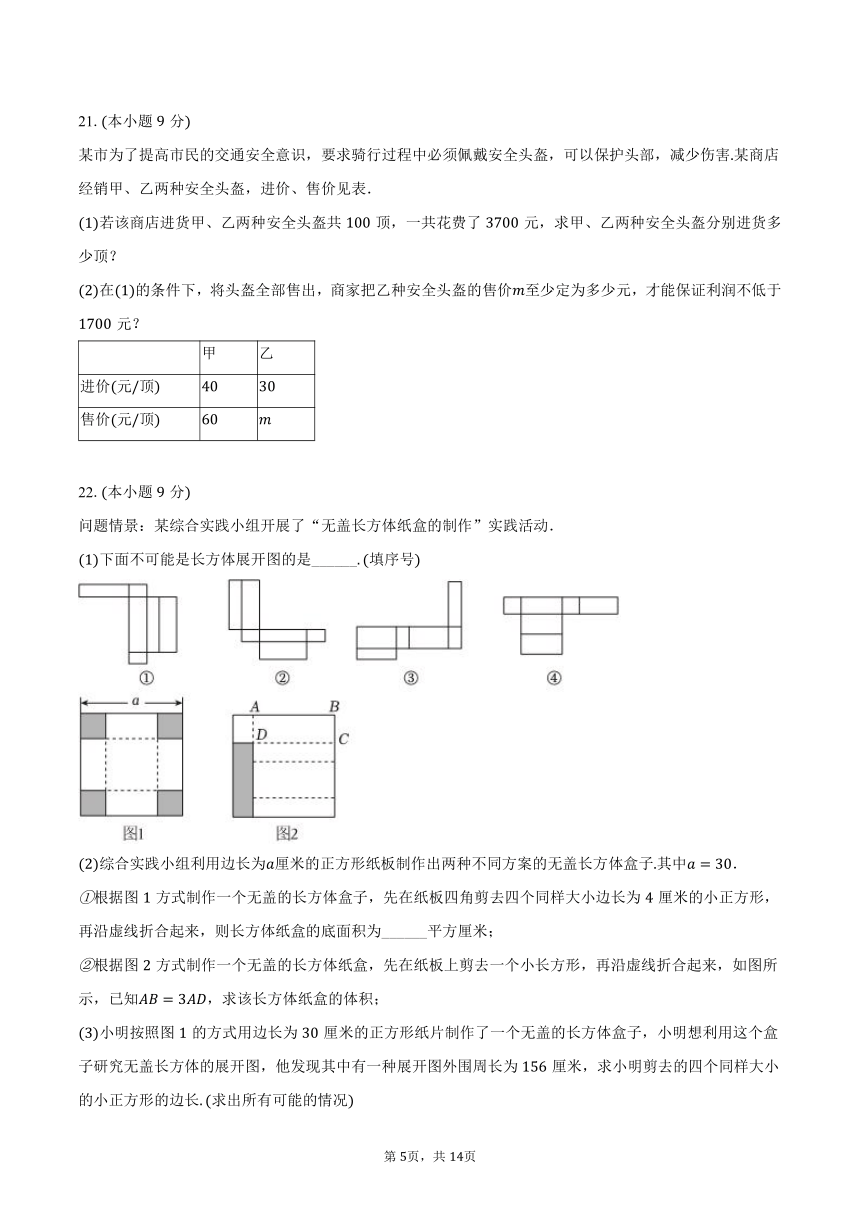
某市为了提高市民的交通安全意识,要求骑行过程中必须佩戴安全头盔,可以保护头部,减少伤害某商店经销甲、乙两种安全头盔,进价、售价见表.
若该商店进货甲、乙两种安全头盔共顶,一共花费了元,求甲、乙两种安全头盔分别进货多少顶?
在的条件下,将头盔全部售出,商家把乙种安全头盔的售价至少定为多少元,才能保证利润不低于元?
甲 乙
进价元顶
售价元顶
22.本小题分
问题情景:某综合实践小组开展了“无盖长方体纸盒的制作”实践活动.
下面不可能是长方体展开图的是______填序号
综合实践小组利用边长为厘米的正方形纸板制作出两种不同方案的无盖长方体盒子其中.
根据图方式制作一个无盖的长方体盒子,先在纸板四角剪去四个同样大小边长为厘米的小正方形,再沿虚线折合起来,则长方体纸盒的底面积为______平方厘米;
根据图方式制作一个无盖的长方体纸盒,先在纸板上剪去一个小长方形,再沿虚线折合起来,如图所示,已知,求该长方体纸盒的体积;
小明按照图的方式用边长为厘米的正方形纸片制作了一个无盖的长方体盒子,小明想利用这个盒子研究无盖长方体的展开图,他发现其中有一种展开图外围周长为厘米,求小明剪去的四个同样大小的小正方形的边长求出所有可能的情况
23.本小题分
综合与实践:【课题学习】:平行线的“等角转化”功能.
如图,已知点是外一点,连接,求的度数.
解:过点作,
______,
又
______.
【问题解决】阅读并补全上述推理过程;
【解题反思】从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将,,“凑”在一起,得出角之间的关系,使问题得以解决.
【方法运用】如图所示,已知,、交于点,,在图的情况下求的度数;
【拓展探究】如图所示,已知,、分别平分和,且、所在直线交于点,过作,若,在图的情况下求的度数.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或或或
13.解:原式
;
得:,
把代入得:,
,
方程组的解为:.
14.解:,
解得:,
解得:.
则不等式组的解集是:,
整数解包括,,,
,
它的所有整数解的和为.
15.解:如图所示,直线即为所求;
如图所示,直线即为所求.
16.解:由题意得:大正方形的面积,
大正方形纸片的边长.
沿此大正方形边的方向,不能裁剪出符合要求的长方形纸片,理由如下:
长方形纸片的长宽之比为:,
设长方形纸片的长和宽分别是,,
,
,
,
,
长方形纸片的长是,
,
沿此大正方形边的方向,不能裁剪出符合要求的长方形纸片.
17.证明:,,
,
,
,
,
,
,
.
18.解:点向上移动个单位长度、向右移动个单位长度,可到到对应点,
点向上移动个单位长度、向右移动个单位长度,可到到对应点,
点向上移动个单位长度、向右移动个单位长度,可到到对应点,
依次连接点,,,如图,即为所求;
;
根据题意可知的边上的高,
由,得:
,
所以,点的坐标为或.
19.,.
.
第一档标准计费所占的百分比为,
所以全市是有的居民每月全部用电支出均可用第一档标准计费.
20.证明:于,
,
在和中,
,
≌,
,
,
,
.
21.解:设甲种安全头盔进货顶,乙种安全头盔进货顶,
根据题意得:,
解得:.
答:甲种安全头盔进货顶,乙种安全头盔进货顶;
根据题意得:,
解得:,
的最小值为.
答:商家把乙种安全头盔的售价至少定为元,才能保证利润不低于元.
22.;
;
如图,设,,
能折成一个无盖长方体纸盒,且,
,
,,
即,
解得:,
立方厘米,
该长方体纸盒的体积为立方厘米;
设小明剪去的小正方形的边长为厘米,
如图所示,
无盖长方体展开图的外围周长为厘米,
,
该方程无解;
如图所示,
无盖长方体展开图的外围周长为厘米,
,
解得:,
如图所示,
无盖长方体展开图的外围周长为厘米,
,
解得:,
如图所示,
无盖长方体展开图的外围周长为厘米,
,
解得:,
如图所示,
无盖长方体展开图的外围周长为厘米,
,
解得:,
综上所述,小明剪去的四个同样大小的小正方形的边长为厘米或厘米或厘米.
23.,;
如图,过点作,
,
,
,
,
,
,
,
,
,
;
如图,过点作,
,
,
,
分别,
,
设,
则,
,
,,
,
,
,
,
,
,
平分,
,
,
,
,
.
第1页,共1页
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列运算正确的是( )
A. B. C. D.
2.如果,那么下列结论错误的是( )
A. B. C. D.
3.如图的两个三角形全等,则的度数为( )
A. B. C. D.
4.如图,在中,,若沿图中的虚线截去,则( )
A.
B.
C.
D.
5.将一个含有的三角板按如图所示,摆放在一组平行线内,,则的度数为( )
A. B. C. D.
6.已知,如图,是内部的一条射线,是射线上任意点,,,下列条件中:,,,,能判定是的角平分线的有( )
A. 个
B. 个
C. 个
D. 个
二、填空题:本题共6小题,每小题3分,共18分。
7.的平方根是______,的算术平方根是______.
8.已知直线轴,且,,则的值为______.
9.已知一个样本有个数据,把它分成组,第一组到第四组的频数分别是、、、,第五组的频率是,则的值为______.
10.若的不等式组有两个整数解,则的取值范围是______.
11.个一样大小的长方形恰好可以拼成一个大的长方形,如图甲所示,若拼成如图乙所示的正方形,中间还留下一个洞,恰好是边长为厘米的小正方形设一个小长方形的长为厘米,宽为厘米,则所列二元一次方程组是______.
12.如图,,垂足为,,,射线,垂足为,动点从点出发以的速度沿射线运动,点为射线上一动点,满足,随着点运动而运动。当点运动__________秒时,与点、、为顶点的三角形全等.
三、解答题:本题共11小题,共84分。解答应写出文字说明,证明过程或演算步骤。
13.本小题分
计算:;
解方程组:.
14.本小题分
解下列不等式组,并求它的所有整数解的和.
15.本小题分
如图,矩形的一条对称轴已经作好,请用一把无刻度的直尺作出矩形的另一条对称轴.
在图中,矩形的边、上分别有、两点,且;请用一把无刻度的直尺作出矩形的一条对称轴.
16.本小题分
【综合与实践】如图,把两个面积均为的小正方形纸片分别沿对角线裁剪后拼成一个大的正方形纸片.
求大正方形纸片的边长;
若沿此大正方形纸片边的方向裁剪出一个长方形纸片,能否使裁剪出的长方形纸片的长宽之比为:,且面积为?若能,求剪出的长方形纸片的长和宽;若不能,试说明理由.
17.本小题分
已知:,,,求证:.
18.本小题分
如图,在平面直角坐标系中,三个顶点的坐标分别是,,,将平移,使点与点重合,得到,点,的对应点分别为、.
画出并写出点、的坐标;
求的面积;
若直线经过点且与轴垂直,点在直线上,且的面积等于,直接写出点的坐标.
19.本小题分
为鼓励居民节约用电,某市对居民用电采用阶梯电价,制定电价收费方案如表一,为了解该市某小区居民用电情况,在该小区随机抽查了户居民某月平均用电量单位:千瓦时记录数据如下:
,,,,,,,,,,,,,,.
,,,,,,,,,,,,,,.
,,,,,,,,,,,,,,
,,,,.
整理数据后得频数分布表如表二.
表一
阶梯电价方案表
档次 月平均用电量千瓦时 电价元千瓦时
第一档
第二档
第三档 大于
表二
某月平均用电量千瓦时 频数
写出 ______, ______;
若根据表二制成扇形统计图,全年月平均用电是不低于千瓦时的部分所对圆心角的度数为______;
请根据抽的数据判断,全市是否有的居民每月全部用电支出均可用第一档标准计费.
20.本小题分
如图,在中,于,分别交、于、两点,且,求证:.
21.本小题分
某市为了提高市民的交通安全意识,要求骑行过程中必须佩戴安全头盔,可以保护头部,减少伤害某商店经销甲、乙两种安全头盔,进价、售价见表.
若该商店进货甲、乙两种安全头盔共顶,一共花费了元,求甲、乙两种安全头盔分别进货多少顶?
在的条件下,将头盔全部售出,商家把乙种安全头盔的售价至少定为多少元,才能保证利润不低于元?
甲 乙
进价元顶
售价元顶
22.本小题分
问题情景:某综合实践小组开展了“无盖长方体纸盒的制作”实践活动.
下面不可能是长方体展开图的是______填序号
综合实践小组利用边长为厘米的正方形纸板制作出两种不同方案的无盖长方体盒子其中.
根据图方式制作一个无盖的长方体盒子,先在纸板四角剪去四个同样大小边长为厘米的小正方形,再沿虚线折合起来,则长方体纸盒的底面积为______平方厘米;
根据图方式制作一个无盖的长方体纸盒,先在纸板上剪去一个小长方形,再沿虚线折合起来,如图所示,已知,求该长方体纸盒的体积;
小明按照图的方式用边长为厘米的正方形纸片制作了一个无盖的长方体盒子,小明想利用这个盒子研究无盖长方体的展开图,他发现其中有一种展开图外围周长为厘米,求小明剪去的四个同样大小的小正方形的边长求出所有可能的情况
23.本小题分
综合与实践:【课题学习】:平行线的“等角转化”功能.
如图,已知点是外一点,连接,求的度数.
解:过点作,
______,
又
______.
【问题解决】阅读并补全上述推理过程;
【解题反思】从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将,,“凑”在一起,得出角之间的关系,使问题得以解决.
【方法运用】如图所示,已知,、交于点,,在图的情况下求的度数;
【拓展探究】如图所示,已知,、分别平分和,且、所在直线交于点,过作,若,在图的情况下求的度数.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或或或
13.解:原式
;
得:,
把代入得:,
,
方程组的解为:.
14.解:,
解得:,
解得:.
则不等式组的解集是:,
整数解包括,,,
,
它的所有整数解的和为.
15.解:如图所示,直线即为所求;
如图所示,直线即为所求.
16.解:由题意得:大正方形的面积,
大正方形纸片的边长.
沿此大正方形边的方向,不能裁剪出符合要求的长方形纸片,理由如下:
长方形纸片的长宽之比为:,
设长方形纸片的长和宽分别是,,
,
,
,
,
长方形纸片的长是,
,
沿此大正方形边的方向,不能裁剪出符合要求的长方形纸片.
17.证明:,,
,
,
,
,
,
,
.
18.解:点向上移动个单位长度、向右移动个单位长度,可到到对应点,
点向上移动个单位长度、向右移动个单位长度,可到到对应点,
点向上移动个单位长度、向右移动个单位长度,可到到对应点,
依次连接点,,,如图,即为所求;
;
根据题意可知的边上的高,
由,得:
,
所以,点的坐标为或.
19.,.
.
第一档标准计费所占的百分比为,
所以全市是有的居民每月全部用电支出均可用第一档标准计费.
20.证明:于,
,
在和中,
,
≌,
,
,
,
.
21.解:设甲种安全头盔进货顶,乙种安全头盔进货顶,
根据题意得:,
解得:.
答:甲种安全头盔进货顶,乙种安全头盔进货顶;
根据题意得:,
解得:,
的最小值为.
答:商家把乙种安全头盔的售价至少定为元,才能保证利润不低于元.
22.;
;
如图,设,,
能折成一个无盖长方体纸盒,且,
,
,,
即,
解得:,
立方厘米,
该长方体纸盒的体积为立方厘米;
设小明剪去的小正方形的边长为厘米,
如图所示,
无盖长方体展开图的外围周长为厘米,
,
该方程无解;
如图所示,
无盖长方体展开图的外围周长为厘米,
,
解得:,
如图所示,
无盖长方体展开图的外围周长为厘米,
,
解得:,
如图所示,
无盖长方体展开图的外围周长为厘米,
,
解得:,
如图所示,
无盖长方体展开图的外围周长为厘米,
,
解得:,
综上所述,小明剪去的四个同样大小的小正方形的边长为厘米或厘米或厘米.
23.,;
如图,过点作,
,
,
,
,
,
,
,
,
,
;
如图,过点作,
,
,
,
分别,
,
设,
则,
,
,,
,
,
,
,
,
,
平分,
,
,
,
,
.
第1页,共1页
同课章节目录
