浙教版2024年秋季九年级(上)第1次月考模拟测试卷 含详解
文档属性
| 名称 | 浙教版2024年秋季九年级(上)第1次月考模拟测试卷 含详解 |

|
|
| 格式 | doc | ||
| 文件大小 | 606.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2024年秋季九年级(上)第1次月考模拟测试卷
数学
(满分120分 时间120分钟)
题号 选择题 填空题 解答题 总分
得分
一.选择题(共10小题,满分30分,每小题3分)
1.下列函数中,是二次函数的是( )
A.y=x B. C.y=x2 D.y=x﹣2
2.随机事件的概率是( )
A.1 B.0 C.大于0且小于1 D.大于1
3.下列事件中是必然事件的是( )
A.某射击运动员射击一次,命中靶心 B.抛掷一枚硬币,落地后正面朝上
C.三角形内角和是360° D.当x是实数时,x2≥0
4.二次函数y=4(x﹣3)2+7的顶点坐标是( )
A.(﹣3,7) B.(3,7) C.(﹣3,﹣7) D.(3,﹣7)
5.在平面直角坐标系中,将抛物线y=x2﹣2x﹣1先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式是( )
A.y=(x+1)2+1 B.y=(x﹣3)2+1
C.y=(x﹣3)2﹣5 D.y=(x+1)2+2
6.一个不透明的口袋中装有8个黑球和若干个白球,每个球除颜色外都相同.摇匀后随机摸一球,已知摸到白球的概率是,估计袋中白球的个数是( )
A.1 B.2 C.3 D.4
7.在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是( )
A. B. C. D.
8.已知二次函数y=3(x﹣1)2+k的图象上有三点A(,y1),B(2,y2),C(﹣,y3),则y1,y2,y3的大小关系为( )
A.y1>y2>y3 B.y2>y1>y3 C.y3>y1>y2 D.y3>y2>y1
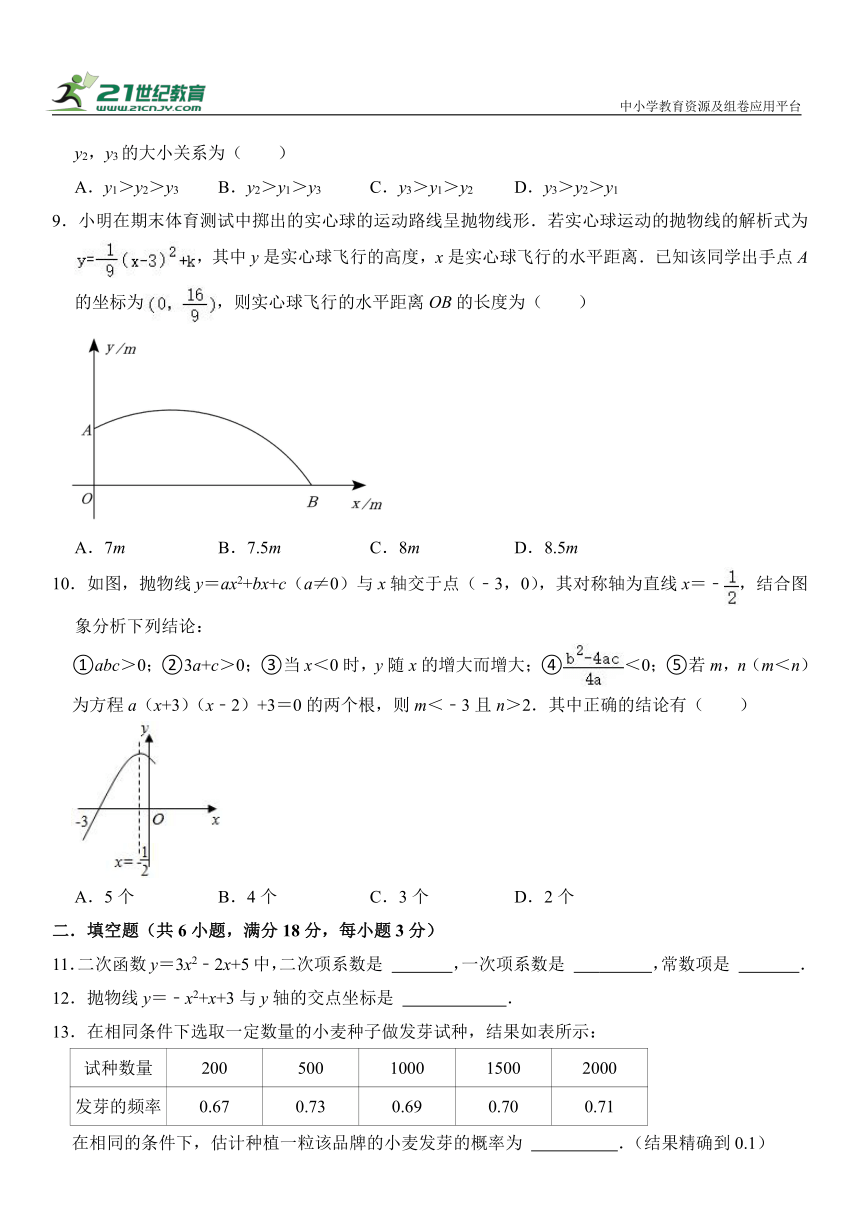
9.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
10.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣,结合图象分析下列结论:
①abc>0;②3a+c>0;③当x<0时,y随x的增大而增大;④<0;⑤若m,n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2.其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
二.填空题(共6小题,满分18分,每小题3分)
11.二次函数y=3x2﹣2x+5中,二次项系数是 ,一次项系数是 ,常数项是 .
12.抛物线y=﹣x2+x+3与y轴的交点坐标是 .
13.在相同条件下选取一定数量的小麦种子做发芽试种,结果如表所示:
试种数量 200 500 1000 1500 2000
发芽的频率 0.67 0.73 0.69 0.70 0.71
在相同的条件下,估计种植一粒该品牌的小麦发芽的概率为 .(结果精确到0.1)
14.二次函数y=ax2+bx+c的图象如图所示,则关于x的不等式ax2+bx+c<0的解集是 .
15.某段公路上汽车紧急刹车后前行的距离s(单位:m)关于行驶时间t(单位:s)的函数解析式是s=30t﹣5t2,遇到刹车时,汽车从刹车后到停下来前进了 m.
16.在平面直角坐标系中,抛物线y=x2的图象如图所示,已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2024的坐标为 .
三.解答题(共8小题,满分72分)
17.(6分)口袋里只有8个球,除颜色外都相同,其中有x个红球,y个白球,没有其他颜色的球,从中随意摸出一个球:(1)如果摸到红球与摸到白球的可能性相等,分别求x和y的值.
(2)在(1)的条件下,现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从口袋中摸出一个球是红球的概率是,求取走多少个白球.
18.(6分)已知抛物线y=ax2+bx+c与x轴的一个交点为A(﹣1,0),对称轴为直线x=1,与y轴的交点为.
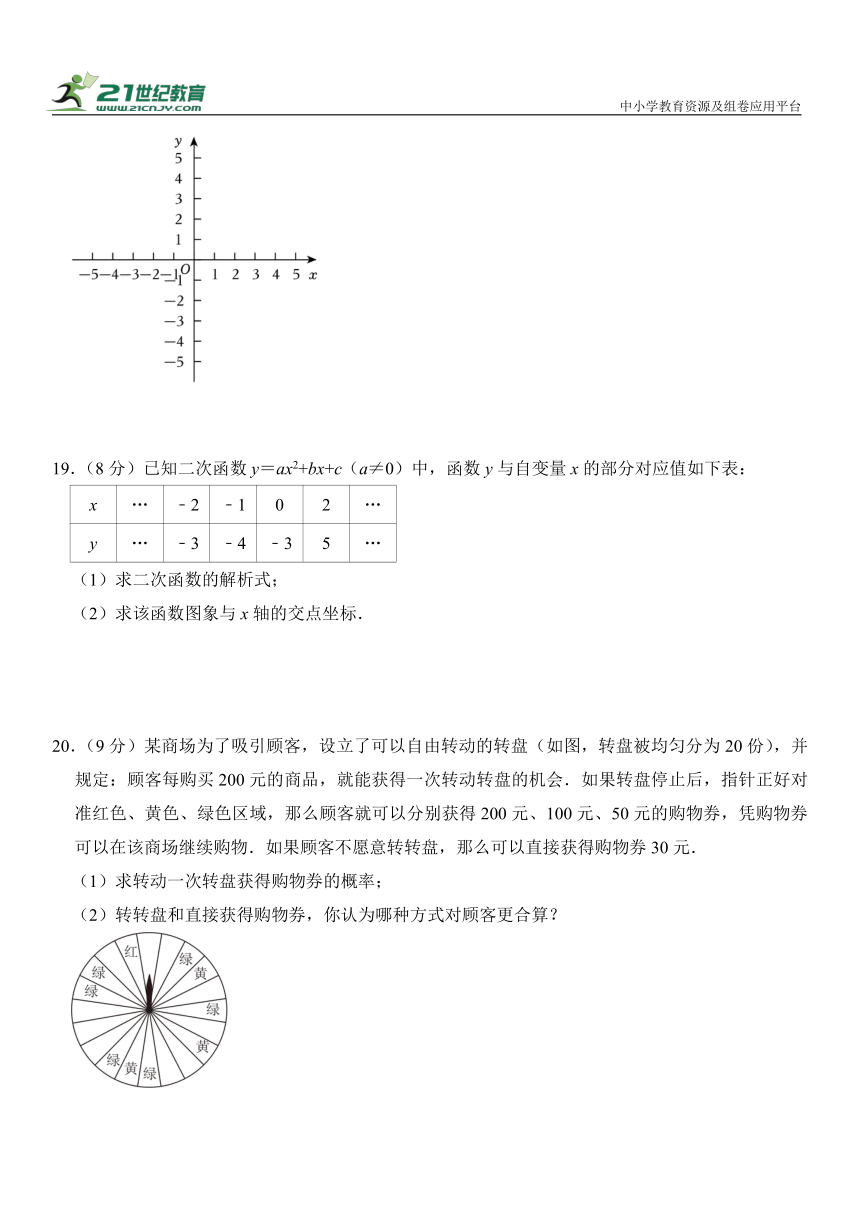
(1)求抛物线解析式,并在如图的平面直角坐标系中画出函数大致图象;
(2)结合图象,当y>0,则x的范围为 .
19.(8分)已知二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如下表:
x … ﹣2 ﹣1 0 2 …
y … ﹣3 ﹣4 ﹣3 5 …
(1)求二次函数的解析式;
(2)求该函数图象与x轴的交点坐标.
20.(9分)某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
21.(9分)已知二次函数y=ax2+bx+c图象与y轴交于点A(0,﹣2),顶点为B(1,﹣3).
(1)求该二次函数解析式.
(2)当2≤x≤6时,求y的取值范围.
22.(10分)已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积.
23.(12分)一水果店售卖一种水果,以8元/千克的价格进货,经过往年销售经验可知:以12元/千克售卖,每天可卖60千克;若每千克涨价0.5元,每天要少卖2千克;若每千克降价0.5元,每天要多卖2千克,但不低于成本价.设该商品的价格为x元/千克时,一天销售总质量为y千克.
(1)求y与x的函数关系式.
(2)若水果店货源充足,每天以固定价格x元/千克销售(x≥8),试求出水果店每天利润W与单价x的函数关系式,并求出当x为何值时,利润达到最大.
24.(12分)如图①,在平面直角坐标系xOy中.抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点B在点A右侧),AB=4,与y轴交于点C.直线y=﹣x+2经过点B,C.
(1)求抛物线的解析式;
(2)如图②,点P为BC上方抛物线上一点,过点P作PE∥x轴交直线BC于点E,作PF∥y轴交直线BC于点F,求△PEF周长的最大值;
(3)在(2)的条件下,若点S是x轴上的动点,点Q为平面内一点,是否存在点S,Q,使得以S,Q,E,F为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
浙教版2024年秋季九年级(上)第1次月考模拟测试卷
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:A、y=x,是正比例函数,故本选项不符合题意;
B、,是反比例函数,故本选项不符合题意;
C、y=x2,符合定义,故本选项符合题意;
D、y=x﹣2,是一次函数,故本选项不符合题意;
故选C.
2.【解答】解:必然事件的概率为1,不可能事件的概率为0,随机事件的概率大于0且小于1.
故选:C.
3.【解答】解:A、某射击运动员射击一次,命中靶心,是随机事件,故本选项不符合题意;
B、抛掷一枚硬币,落地后正面朝上,是随机事件,故本选项不符合题意;
C、三角形内角和是360°,是不可能事件,故本选项不符合题意;
D、当x是实数时,x2≥0,是必然事件,故本选项符合题意.
故选:D.
4.【解答】解:∵y=4(x﹣3)2+7,
∴顶点坐标为(3,7),
故选:B.
5.【解答】解:抛物线y=x2﹣2x﹣1可化简为y=(x﹣1)2﹣2,先向上平移3个单位长度,再向左平移2个单位长度,
所得的抛物线的解析式y=(x﹣1+2)2﹣2+3=(x+1)2+1;
故选:A.
6.【解答】解:设袋子中白球的个数为x个,
则,
解得x=4,
经检验得x=4是原方程的解,
∴估计袋中白球的个数是4个.
故选:D.
7.【解答】解:A、由直线y=ax+b的图象经过第二、三、四象限可知:a<0,b<0,
二次函数y=ax2﹣b的图象开口向上,
∴a>0,A不正确;
B、由直线y=ax+b的图象经过第一、二、三象限可知:a>0,b>0,
二次函数y=ax2﹣b的图象开口向下,
∴a<0,B不正确;
C、由直线y=ax+b的图象经过第一、二、四象限可知:a<0,b>0,
二次函数y=ax2﹣b的图象开口向上,
∴a>0,C不正确;
D、由直线y=ax+b的图象经过第一、二、三象限可知:a>0,b>0,
二次函数y=ax2﹣b的图象开口向上,顶点在y轴负半轴,
∴a>0,b>0,D正确.
故选:D.
8.【解答】解:函数y=3(x﹣1)2+k,对称轴x=1,
在图象上的三点A(,y1),B(2,y2),C(﹣,y3),
||<|2﹣1|<||,根据横坐标离对称轴越近,则纵坐标越小,
则y1、y2、y3的大小关系为y3>y2>y1.
故选:D.
9.【解答】解:把A代入得:
=﹣×9+k,
∴k=,
∴y=﹣(x﹣3)2+,
令y=0得﹣(x﹣3)2+=0,
解得x=﹣2(舍去)或x=8,
∴实心球飞行的水平距离OB的长度为8m,
故选:C.
10.【解答】解:由抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣可得,
9a﹣3b+c=0,﹣=﹣,即a=b,与x轴的另一个交点为(2,0),4a+2b+c=0,
抛物线开口向下,a<0,b<0,
抛物线与y轴交于正半轴,因此c>0,
所以,abc>0,因此①正确;
由9a﹣3b+c=0,而a=b,
所以6a+c=0,又a<0,
因此3a+c>0,所以②正确;
抛物线的对称轴为x=﹣,a<0,因此当x<﹣时,y随x的增大而增大,所以③不正确;
由于抛物线的顶点在第二象限,所以>0,因此<0,故④正确;
抛物线与x轴的交点为(﹣3,0),(2,0),
因此当y=﹣3时,相应的x的值应在(﹣3,0)的左侧和(2,0)的右侧,
因此m<﹣3,n>2,所以⑤正确;
综上所述,正确的结论有:①②④⑤,
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:由y=3x2﹣2x+5,得它的二次项系数是3,一次项系数是﹣2,常数项是5.
故答案是:3,﹣2,5.
12.【解答】解:当x=0时,y=﹣x2+x+3=3,
∴抛物线y=﹣x2+x+3与y轴交点坐标为(0,3).
故答案为:(0,3).
13.【解答】解:估计种植一粒该品牌的小麦发芽的概率为0.71≈0.7.
故答案为:0.7.
14.【解答】解:由图象可知,关于x的不等式ax2+bx+c<0的解集是﹣1<x<3.
故答案为:﹣1<x<3.
15.【解答】解:∵s=﹣5t2+30t=﹣5(t﹣3)2+45,
∴汽车刹车后到停下来前进了45m,
故答案为:45.
16.【解答】解:∵A点坐标为(1,1),AA1∥x轴交抛物线于点A1,
∴直线OA为y=x,A1的坐标(﹣1,1),
∵A1A2∥OA,
∴直线A1A2为y=x+2,
∴,
解得:或,
∴A2(2,4),
∵A2A3∥x轴,
∴A3(﹣2,4),
∵A3A4∥OA,
∴直线A3A4为y=x+6,
∴,
解得:或,
∴A4(3,9),
∴A5(﹣3,9),
……,
∴n为奇数时,An(﹣,()2),
n为偶数时,An(,()2),
∴A2024(1013,10132),
故答案为:(1013,10132).
三.解答题(共8小题,满分72分)
17.【解答】解:(1)∵摸到红球与摸到白球的可能性相等,且x+y=8,
∴x=y=4;
(2)设取走x个白球,放入x个红球,则口袋中现在有白球(4﹣x)个,红球(4+x)个,
根据题意得,=,
解得x=3,
答:取走3个白球.
18.【解答】解:(1)由题意可得,,
解得,
∴抛物线解析式为;
函数图象如下所示:
(2)在中,当时,
解得x=﹣1或x=3,
∴由函数图象可知,当y>0,则x的范围为﹣1<x<3,
故答案为:﹣1<x<3.
19.【解答】解:(1)由题意,得c=﹣3.
将点(2,5),(﹣1,﹣4)代入,
得,
解得,
∴二次函数的解析式为y=x2+2x﹣3;
(2)当y=0时,x2+2x﹣3=0,
解得:x=﹣3或x=1,
∴该函数图象与x轴的交点坐标(﹣3,0),(1,0).
20.【解答】解:(1)∵转盘被均匀分为20份,转动一次转盘获得购物券的有10种情况,
∴P(转动一次转盘获得购物券)==.
(2)∵P(红色)=,P(黄色)=,P(绿色)==,
∴200×+100×+×50=40(元)
∵40元>30元,
∴选择转转盘对顾客更合算.
21.【解答】解:(1)由题意可知二次函数y=a(x﹣1)2﹣3,
代入点A(0,﹣2)得,﹣2=a﹣3,
解得a=1,
∴该二次函数解析式为y=(x﹣1)2﹣3;
(2)抛物线y=(x﹣1)2﹣3的开口向上,对称轴为直线x=1,函数有最小值为﹣3,
∴当x>1时,y随x的增大而增大,
当x=6时,y=(6﹣1)2﹣3=22,
当x=2时,y=(2﹣1)2﹣3=﹣2,
∴当2≤x≤6时,y的取值范围是﹣2≤y≤22.
22.【解答】解:(1)∵二次函数y=ax2+bx+c的图象经过点(0,5),(1,8),(﹣1,0),
∴c=5,
把(1,8),(﹣1,0)分别代入二次函数,得
,
解得a=﹣1,b=4,
∴抛物线的解析式:y=﹣x2+4x+5;
(2)过点M作ME⊥x轴,交BC于D,如图所示:
∵y=﹣x2+4x+5
=﹣(x﹣2)2+9;
∴M(2,9),B(5,0),
设直线BC:y=kx+b,
把B(5,0),C(0,5),分别代入一次函数,得
,
解得k=﹣1,
∴直线BC:y=﹣x+5,
∵ME⊥x轴,
∴MD∥y轴,
∴把x=2代入y=﹣x+5,
得y=3,
∴D(2,3),
∴MD=6,
∴△MCB的面积=
=×5
=15.
23.【解答】解:(1)由题意可得,y=60﹣×2=﹣4x+108;
(2)由题意可得,W=y(x﹣8)=(﹣4x+108)(x﹣8)=﹣4x2+140x﹣864=﹣4(x﹣)2+361,
∵﹣4<0,
∴当时,利润W达到最大,最大值为361,
答:当x为时,利润达到最大.
24.【解答】解:(1)直线y=﹣x+2,令x=0得y=2,
令y=0得﹣x+2=0,解得x=3.
∴B (3,0),C(0,2),
∵AB=4,
∴A(﹣1,0),
将A(﹣1,0),B (3,0),C(0,2)代入y=ax2+bx+c得,
,解得,
∴抛物线的解析式为y=﹣x2+x+2;
(2)设点P(m,﹣m2+m+2),
∵PE∥x轴,
∴﹣m2+m+2=﹣xE+2,,
∴xE=m2﹣2m,
∴E(m2﹣2m,﹣m2+m+2),
∵PF∥y轴,
∴F(m,﹣m+2),
∴PE=m﹣(m2﹣2m)=﹣m2+3m,
PF=﹣m2+m+2﹣(﹣m+2)=﹣m2+2m,
EF==|m2﹣3m|,
∵点P为BC上方抛物线上一点,
∴0<m<3,
∴EF=(3m﹣m2),
∴△PEF的周长=﹣m2+3m+(﹣m2+2m)+(3m﹣m2)=﹣(m﹣)2+,
∵﹣<0,
∴当m=时,△PEF周长的最大值为;
(3)存在,
由(2)知m=时,E(﹣,),F(,1),
∴EF==,
设S(s,0),
①线段EF为菱形的边,四边形EFQS为菱形时,如图,
∴ES=EF,
∴=,
∴s=,
∴S(,0)或(,0),
∵四边形EFQS为菱形,点F的坐标可由点E向右平移个单位长度,向下平移个单位长度得到,
∴点Q可由点S向右平移个单位长度,向下平移个单位长度得到,
∴Q(,﹣)或(,﹣);
②线段EF为菱形的边,四边形EQSF为菱形时,如图,
∴FS=EF,
∴=,
∴s=,
∴S(,0)或(,0),
∵四边形EQSF为菱形,点E的坐标可由点F向左平移个单位长度,向上平移个单位长度得到,
∴点Q可由点S向左平移个单位长度,向上平移个单位长度得到,
∴Q(,)或(,);
③线段EF为菱形的对角线,四边形EQFS为菱形时,如图,
∴ES=FS,
∴=,
∴s=﹣,
设Q(p,q),
∴p﹣=﹣+,解得p=,
q+0=+1,解得q=,
∴Q(,).
综上所述,存在,点Q的坐标为(,﹣)或(,﹣)或(,)或(,)或(,).
浙教版2024年秋季九年级(上)第1次月考模拟测试卷
数学
(满分120分 时间120分钟)
题号 选择题 填空题 解答题 总分
得分
一.选择题(共10小题,满分30分,每小题3分)
1.下列函数中,是二次函数的是( )
A.y=x B. C.y=x2 D.y=x﹣2
2.随机事件的概率是( )
A.1 B.0 C.大于0且小于1 D.大于1
3.下列事件中是必然事件的是( )
A.某射击运动员射击一次,命中靶心 B.抛掷一枚硬币,落地后正面朝上
C.三角形内角和是360° D.当x是实数时,x2≥0
4.二次函数y=4(x﹣3)2+7的顶点坐标是( )
A.(﹣3,7) B.(3,7) C.(﹣3,﹣7) D.(3,﹣7)
5.在平面直角坐标系中,将抛物线y=x2﹣2x﹣1先向上平移3个单位长度,再向左平移2个单位长度,所得的抛物线的解析式是( )
A.y=(x+1)2+1 B.y=(x﹣3)2+1
C.y=(x﹣3)2﹣5 D.y=(x+1)2+2
6.一个不透明的口袋中装有8个黑球和若干个白球,每个球除颜色外都相同.摇匀后随机摸一球,已知摸到白球的概率是,估计袋中白球的个数是( )
A.1 B.2 C.3 D.4
7.在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是( )
A. B. C. D.
8.已知二次函数y=3(x﹣1)2+k的图象上有三点A(,y1),B(2,y2),C(﹣,y3),则y1,y2,y3的大小关系为( )
A.y1>y2>y3 B.y2>y1>y3 C.y3>y1>y2 D.y3>y2>y1
9.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
10.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣,结合图象分析下列结论:
①abc>0;②3a+c>0;③当x<0时,y随x的增大而增大;④<0;⑤若m,n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2.其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
二.填空题(共6小题,满分18分,每小题3分)
11.二次函数y=3x2﹣2x+5中,二次项系数是 ,一次项系数是 ,常数项是 .
12.抛物线y=﹣x2+x+3与y轴的交点坐标是 .
13.在相同条件下选取一定数量的小麦种子做发芽试种,结果如表所示:
试种数量 200 500 1000 1500 2000
发芽的频率 0.67 0.73 0.69 0.70 0.71
在相同的条件下,估计种植一粒该品牌的小麦发芽的概率为 .(结果精确到0.1)
14.二次函数y=ax2+bx+c的图象如图所示,则关于x的不等式ax2+bx+c<0的解集是 .
15.某段公路上汽车紧急刹车后前行的距离s(单位:m)关于行驶时间t(单位:s)的函数解析式是s=30t﹣5t2,遇到刹车时,汽车从刹车后到停下来前进了 m.
16.在平面直角坐标系中,抛物线y=x2的图象如图所示,已知A点坐标为(1,1),过点A作AA1∥x轴交抛物线于点A1,过点A1作A1A2∥OA交抛物线于点A2,过点A2作A2A3∥x轴交抛物线于点A3,过点A3作A3A4∥OA交抛物线于点A4……,依次进行下去,则点A2024的坐标为 .
三.解答题(共8小题,满分72分)
17.(6分)口袋里只有8个球,除颜色外都相同,其中有x个红球,y个白球,没有其他颜色的球,从中随意摸出一个球:(1)如果摸到红球与摸到白球的可能性相等,分别求x和y的值.
(2)在(1)的条件下,现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从口袋中摸出一个球是红球的概率是,求取走多少个白球.
18.(6分)已知抛物线y=ax2+bx+c与x轴的一个交点为A(﹣1,0),对称轴为直线x=1,与y轴的交点为.
(1)求抛物线解析式,并在如图的平面直角坐标系中画出函数大致图象;
(2)结合图象,当y>0,则x的范围为 .
19.(8分)已知二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如下表:
x … ﹣2 ﹣1 0 2 …
y … ﹣3 ﹣4 ﹣3 5 …
(1)求二次函数的解析式;
(2)求该函数图象与x轴的交点坐标.
20.(9分)某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
21.(9分)已知二次函数y=ax2+bx+c图象与y轴交于点A(0,﹣2),顶点为B(1,﹣3).
(1)求该二次函数解析式.
(2)当2≤x≤6时,求y的取值范围.
22.(10分)已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积.
23.(12分)一水果店售卖一种水果,以8元/千克的价格进货,经过往年销售经验可知:以12元/千克售卖,每天可卖60千克;若每千克涨价0.5元,每天要少卖2千克;若每千克降价0.5元,每天要多卖2千克,但不低于成本价.设该商品的价格为x元/千克时,一天销售总质量为y千克.
(1)求y与x的函数关系式.
(2)若水果店货源充足,每天以固定价格x元/千克销售(x≥8),试求出水果店每天利润W与单价x的函数关系式,并求出当x为何值时,利润达到最大.
24.(12分)如图①,在平面直角坐标系xOy中.抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点B在点A右侧),AB=4,与y轴交于点C.直线y=﹣x+2经过点B,C.
(1)求抛物线的解析式;
(2)如图②,点P为BC上方抛物线上一点,过点P作PE∥x轴交直线BC于点E,作PF∥y轴交直线BC于点F,求△PEF周长的最大值;
(3)在(2)的条件下,若点S是x轴上的动点,点Q为平面内一点,是否存在点S,Q,使得以S,Q,E,F为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.
浙教版2024年秋季九年级(上)第1次月考模拟测试卷
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:A、y=x,是正比例函数,故本选项不符合题意;
B、,是反比例函数,故本选项不符合题意;
C、y=x2,符合定义,故本选项符合题意;
D、y=x﹣2,是一次函数,故本选项不符合题意;
故选C.
2.【解答】解:必然事件的概率为1,不可能事件的概率为0,随机事件的概率大于0且小于1.
故选:C.
3.【解答】解:A、某射击运动员射击一次,命中靶心,是随机事件,故本选项不符合题意;
B、抛掷一枚硬币,落地后正面朝上,是随机事件,故本选项不符合题意;
C、三角形内角和是360°,是不可能事件,故本选项不符合题意;
D、当x是实数时,x2≥0,是必然事件,故本选项符合题意.
故选:D.
4.【解答】解:∵y=4(x﹣3)2+7,
∴顶点坐标为(3,7),
故选:B.
5.【解答】解:抛物线y=x2﹣2x﹣1可化简为y=(x﹣1)2﹣2,先向上平移3个单位长度,再向左平移2个单位长度,
所得的抛物线的解析式y=(x﹣1+2)2﹣2+3=(x+1)2+1;
故选:A.
6.【解答】解:设袋子中白球的个数为x个,
则,
解得x=4,
经检验得x=4是原方程的解,
∴估计袋中白球的个数是4个.
故选:D.
7.【解答】解:A、由直线y=ax+b的图象经过第二、三、四象限可知:a<0,b<0,
二次函数y=ax2﹣b的图象开口向上,
∴a>0,A不正确;
B、由直线y=ax+b的图象经过第一、二、三象限可知:a>0,b>0,
二次函数y=ax2﹣b的图象开口向下,
∴a<0,B不正确;
C、由直线y=ax+b的图象经过第一、二、四象限可知:a<0,b>0,
二次函数y=ax2﹣b的图象开口向上,
∴a>0,C不正确;
D、由直线y=ax+b的图象经过第一、二、三象限可知:a>0,b>0,
二次函数y=ax2﹣b的图象开口向上,顶点在y轴负半轴,
∴a>0,b>0,D正确.
故选:D.
8.【解答】解:函数y=3(x﹣1)2+k,对称轴x=1,
在图象上的三点A(,y1),B(2,y2),C(﹣,y3),
||<|2﹣1|<||,根据横坐标离对称轴越近,则纵坐标越小,
则y1、y2、y3的大小关系为y3>y2>y1.
故选:D.
9.【解答】解:把A代入得:
=﹣×9+k,
∴k=,
∴y=﹣(x﹣3)2+,
令y=0得﹣(x﹣3)2+=0,
解得x=﹣2(舍去)或x=8,
∴实心球飞行的水平距离OB的长度为8m,
故选:C.
10.【解答】解:由抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣可得,
9a﹣3b+c=0,﹣=﹣,即a=b,与x轴的另一个交点为(2,0),4a+2b+c=0,
抛物线开口向下,a<0,b<0,
抛物线与y轴交于正半轴,因此c>0,
所以,abc>0,因此①正确;
由9a﹣3b+c=0,而a=b,
所以6a+c=0,又a<0,
因此3a+c>0,所以②正确;
抛物线的对称轴为x=﹣,a<0,因此当x<﹣时,y随x的增大而增大,所以③不正确;
由于抛物线的顶点在第二象限,所以>0,因此<0,故④正确;
抛物线与x轴的交点为(﹣3,0),(2,0),
因此当y=﹣3时,相应的x的值应在(﹣3,0)的左侧和(2,0)的右侧,
因此m<﹣3,n>2,所以⑤正确;
综上所述,正确的结论有:①②④⑤,
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:由y=3x2﹣2x+5,得它的二次项系数是3,一次项系数是﹣2,常数项是5.
故答案是:3,﹣2,5.
12.【解答】解:当x=0时,y=﹣x2+x+3=3,
∴抛物线y=﹣x2+x+3与y轴交点坐标为(0,3).
故答案为:(0,3).
13.【解答】解:估计种植一粒该品牌的小麦发芽的概率为0.71≈0.7.
故答案为:0.7.
14.【解答】解:由图象可知,关于x的不等式ax2+bx+c<0的解集是﹣1<x<3.
故答案为:﹣1<x<3.
15.【解答】解:∵s=﹣5t2+30t=﹣5(t﹣3)2+45,
∴汽车刹车后到停下来前进了45m,
故答案为:45.
16.【解答】解:∵A点坐标为(1,1),AA1∥x轴交抛物线于点A1,
∴直线OA为y=x,A1的坐标(﹣1,1),
∵A1A2∥OA,
∴直线A1A2为y=x+2,
∴,
解得:或,
∴A2(2,4),
∵A2A3∥x轴,
∴A3(﹣2,4),
∵A3A4∥OA,
∴直线A3A4为y=x+6,
∴,
解得:或,
∴A4(3,9),
∴A5(﹣3,9),
……,
∴n为奇数时,An(﹣,()2),
n为偶数时,An(,()2),
∴A2024(1013,10132),
故答案为:(1013,10132).
三.解答题(共8小题,满分72分)
17.【解答】解:(1)∵摸到红球与摸到白球的可能性相等,且x+y=8,
∴x=y=4;
(2)设取走x个白球,放入x个红球,则口袋中现在有白球(4﹣x)个,红球(4+x)个,
根据题意得,=,
解得x=3,
答:取走3个白球.
18.【解答】解:(1)由题意可得,,
解得,
∴抛物线解析式为;
函数图象如下所示:
(2)在中,当时,
解得x=﹣1或x=3,
∴由函数图象可知,当y>0,则x的范围为﹣1<x<3,
故答案为:﹣1<x<3.
19.【解答】解:(1)由题意,得c=﹣3.
将点(2,5),(﹣1,﹣4)代入,
得,
解得,
∴二次函数的解析式为y=x2+2x﹣3;
(2)当y=0时,x2+2x﹣3=0,
解得:x=﹣3或x=1,
∴该函数图象与x轴的交点坐标(﹣3,0),(1,0).
20.【解答】解:(1)∵转盘被均匀分为20份,转动一次转盘获得购物券的有10种情况,
∴P(转动一次转盘获得购物券)==.
(2)∵P(红色)=,P(黄色)=,P(绿色)==,
∴200×+100×+×50=40(元)
∵40元>30元,
∴选择转转盘对顾客更合算.
21.【解答】解:(1)由题意可知二次函数y=a(x﹣1)2﹣3,
代入点A(0,﹣2)得,﹣2=a﹣3,
解得a=1,
∴该二次函数解析式为y=(x﹣1)2﹣3;
(2)抛物线y=(x﹣1)2﹣3的开口向上,对称轴为直线x=1,函数有最小值为﹣3,
∴当x>1时,y随x的增大而增大,
当x=6时,y=(6﹣1)2﹣3=22,
当x=2时,y=(2﹣1)2﹣3=﹣2,
∴当2≤x≤6时,y的取值范围是﹣2≤y≤22.
22.【解答】解:(1)∵二次函数y=ax2+bx+c的图象经过点(0,5),(1,8),(﹣1,0),
∴c=5,
把(1,8),(﹣1,0)分别代入二次函数,得
,
解得a=﹣1,b=4,
∴抛物线的解析式:y=﹣x2+4x+5;
(2)过点M作ME⊥x轴,交BC于D,如图所示:
∵y=﹣x2+4x+5
=﹣(x﹣2)2+9;
∴M(2,9),B(5,0),
设直线BC:y=kx+b,
把B(5,0),C(0,5),分别代入一次函数,得
,
解得k=﹣1,
∴直线BC:y=﹣x+5,
∵ME⊥x轴,
∴MD∥y轴,
∴把x=2代入y=﹣x+5,
得y=3,
∴D(2,3),
∴MD=6,
∴△MCB的面积=
=×5
=15.
23.【解答】解:(1)由题意可得,y=60﹣×2=﹣4x+108;
(2)由题意可得,W=y(x﹣8)=(﹣4x+108)(x﹣8)=﹣4x2+140x﹣864=﹣4(x﹣)2+361,
∵﹣4<0,
∴当时,利润W达到最大,最大值为361,
答:当x为时,利润达到最大.
24.【解答】解:(1)直线y=﹣x+2,令x=0得y=2,
令y=0得﹣x+2=0,解得x=3.
∴B (3,0),C(0,2),
∵AB=4,
∴A(﹣1,0),
将A(﹣1,0),B (3,0),C(0,2)代入y=ax2+bx+c得,
,解得,
∴抛物线的解析式为y=﹣x2+x+2;
(2)设点P(m,﹣m2+m+2),
∵PE∥x轴,
∴﹣m2+m+2=﹣xE+2,,
∴xE=m2﹣2m,
∴E(m2﹣2m,﹣m2+m+2),
∵PF∥y轴,
∴F(m,﹣m+2),
∴PE=m﹣(m2﹣2m)=﹣m2+3m,
PF=﹣m2+m+2﹣(﹣m+2)=﹣m2+2m,
EF==|m2﹣3m|,
∵点P为BC上方抛物线上一点,
∴0<m<3,
∴EF=(3m﹣m2),
∴△PEF的周长=﹣m2+3m+(﹣m2+2m)+(3m﹣m2)=﹣(m﹣)2+,
∵﹣<0,
∴当m=时,△PEF周长的最大值为;
(3)存在,
由(2)知m=时,E(﹣,),F(,1),
∴EF==,
设S(s,0),
①线段EF为菱形的边,四边形EFQS为菱形时,如图,
∴ES=EF,
∴=,
∴s=,
∴S(,0)或(,0),
∵四边形EFQS为菱形,点F的坐标可由点E向右平移个单位长度,向下平移个单位长度得到,
∴点Q可由点S向右平移个单位长度,向下平移个单位长度得到,
∴Q(,﹣)或(,﹣);
②线段EF为菱形的边,四边形EQSF为菱形时,如图,
∴FS=EF,
∴=,
∴s=,
∴S(,0)或(,0),
∵四边形EQSF为菱形,点E的坐标可由点F向左平移个单位长度,向上平移个单位长度得到,
∴点Q可由点S向左平移个单位长度,向上平移个单位长度得到,
∴Q(,)或(,);
③线段EF为菱形的对角线,四边形EQFS为菱形时,如图,
∴ES=FS,
∴=,
∴s=﹣,
设Q(p,q),
∴p﹣=﹣+,解得p=,
q+0=+1,解得q=,
∴Q(,).
综上所述,存在,点Q的坐标为(,﹣)或(,﹣)或(,)或(,)或(,).
同课章节目录
