冀教版2024-2025学年六年级数学上册4.1圆的周长同步练习【提升版】(含解析)
文档属性
| 名称 | 冀教版2024-2025学年六年级数学上册4.1圆的周长同步练习【提升版】(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 432.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 17:06:14 | ||
图片预览




文档简介
冀教版2024-2025学年六年级数学上册4.1圆的周长同步练习【基础版】
学校:__________ 姓名:___________ 班级:___________
一、选择题
1.用圆规画一个周长是25.12cm的圆,圆规两脚之间的距离是( )cm。
A.8 B.4 C.2 D.1
2.大圆的半径等于小圆的直径,大圆的周长是小圆的周长的( )。
A.2倍 B. C.4倍 D.
3.用两根长度相等的铁丝分别正好围成一个正方形和一个圆,下列说法中正确的是( )。
A.正方形的面积大 B.圆的面积大 C.它们的面积一样大
4.把一个直径是10cm的圆沿直径分成两个半圆,这两个半圆的周长之和是( )。
A.31.4cm B.41.4cm C.51.4cm D.61.4cm
5.一个圆的周长、直径、半径的和是18.56厘米,这个圆的直径是( )厘米。
A.2 B.3 C.3.14 D.4
二、填空题
6.我国魏晋时期杰出的数学家刘徽得出了较精确的圆周率的值,他采用“( )”一直算到圆内接正192边形,得出圆周率的近似值是3.14。
7.观察下图,你发现了什么?
分析与解答:我们可以把汽车雨刷器看成一条( ),这条( )转动后形成一个( ),这是一个( )图形。
8.已知圆的周长是18.84dm,则这个圆的半径是( )dm。
9.一个直径是8cm的半圆形零件,周长是( )cm,面积是( )cm2。
10.用一根长为18.84m的绳子围成一个圆,这个圆的直径为( )m,半径为( )m。
11.一年级小朋友两臂伸平后长度约是1.2米,32个小朋友手拉手围成一个圆圈做投掷游戏,靶子放在围成的圆圈中心位置,每个小朋友距离靶子大约是( )米。其中,距离最远的两名小朋友之间的距离是( )米。(得数都保留整数)
12.甲、乙两辆汽车同时从A、B两地相向而行,甲汽车每小时行驶90千米,乙汽车每小时行驶80千米,两辆汽车相遇时距离全程中点20千米,则相遇时他们各行了 小时,全程长 千米。
三、判断题
13.如果两个圆的周长相等,那么它们的面积也相等。( )
14.任何一条直径所在的直线都是圆的对称轴,圆有无数条对称轴。( )
15.圆和半圆都是轴对称图形,它们都有无数条对称轴。( )
16.若大圆的直径为d1,小圆的直径为d2,则两圆的周长相差π(d1-d2)。( )
17.圆的面积就是围成圆的曲线的长度。( )
四、计算题
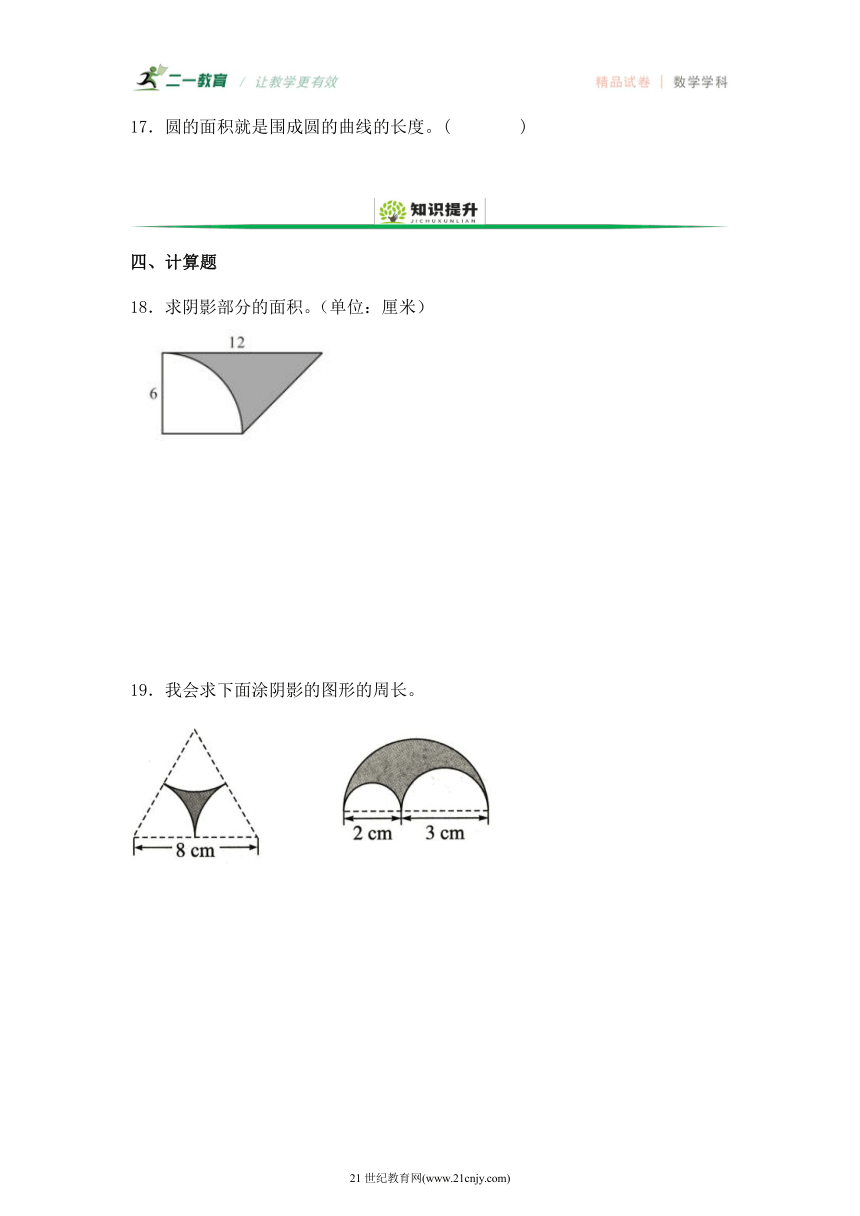
18.求阴影部分的面积。(单位:厘米)
19.我会求下面涂阴影的图形的周长。
五、解答题
20.芳芳和刚刚在学校操场400米的环形跑道上同时同地出发背向而行,芳芳每分钟走35米,刚刚每分钟走45米。两人第一次遇到时芳芳走了多少米?
21.某俱乐部有一个圆形舞池,周长为37.68米,现准备把半径加长1米,舞池面积可增加多少平方米?
21世纪教育网(www.21cnjy.com)
1.B
【分析】画圆时,圆规两脚之间的距离是半径,根据半径=圆的周长÷圆周率÷2,列式计算即可。
【详解】25.12÷3.14÷2=4(cm)
圆规两脚之间的距离是4cm。
故答案为:B
2.A
【分析】根据题意可知,大圆的半径等于小圆的直径;由此可知,大圆的半径等于小圆半径的2倍,设小圆半径为r,则大圆半径为2r,根据圆的周长公式:周长=π×半径×2,分别求出大圆周长和小圆周长,再用大圆周长÷小圆周长,即可解答。
【详解】设小圆半径为r,则大圆半径为2r。
(π×2r×2)÷(πr×2)
=(4πr)÷(2πr)
=2
大圆的半径等于小圆的直径,大圆的周长是小圆的周长的2倍。
故答案为:A
3.B
【分析】设铁丝的长是12.56厘米,根据正方形周长公式:周长=边长×4,边长=周长÷4,代入数据,求出正方形边长;再根据正方形面积公式:面积=边长×边长,求出正方形面积;
根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆的半径,再根据圆的面积公式:面积=π×半径2,代入数据,求出圆的面积,再进行比较,即可解答。
【详解】设铁丝的长是12.56厘米。
正方形边长:12.56÷4=3.14(厘米)
正方形面积:3.14×3.14=9.8596(平方厘米)
圆的半径:
12.56÷3.14÷2
=4÷2
=2(厘米)
圆的面积:
3.14×22
=3.14×4
=12.56(平方厘米)
9.8596<12.56,圆的面积大。
用两根长度相等的铁丝分别正好围成一个正方形和一个圆,圆的面积大。
故答案为:B
4.C
【分析】根据题意,把一个圆沿直径分成两个半圆,根据半圆的周长=圆周长的一半+直径=πd÷2+d,据此求出一个半圆的周长,再乘2,即是这两个半圆的周长之和。
【详解】3.14×10÷2+10
=15.7+10
=25.7(cm)
25.7×2=51.4(cm)
这两个半圆的周长之和是51.4cm。
故答案为:C
5.D
【分析】根据d=2r,C=2πr,可知2r+r+2πr=18.56,根据等式的性质求出r,也就是半径,进而求出直径。
【详解】2r+r+2πr=18.56
解:2r+r+2×3.14×r=18.56
2r+r+6.28r=18.56
9.28r=18.56
r=18.56÷9.28
r=2
2×2=4(厘米)
这个圆的直径是4厘米。
故答案为:D
【点睛】本题主要考查了圆周长公式的灵活应用,要熟练掌握相关公式。
6.割圆术
【详解】通过学习我们知道,圆周率是圆的周长和直径的比值。我国魏晋时期杰出的数学家刘徽得出了较精确的圆周率的值,他采用“割圆术”一直算到圆内接正192边形,得出圆周率的近似值是3.14。
7. 线段 线段 扇形 平面
【详解】由点动成线,线动成面,面动成体可知:我们可以把汽车雨刷器看成一条线段,这条线段转动后形成一个扇形,这是一个平面图形。
8.3
【分析】圆的周长,代入数据求出这个圆的半径即可。
【详解】
(dm)
所以这个圆的半径是3dm。
9. 20.56 25.12
【分析】根据圆的周长公式:周长=π×直径,代入数据,求出直径是8cm的圆的周长,再除以2,求出直径是8cm圆的周长一半,再加上直径的长度,即可求出这个半圆形零件的周长;面积就是直径是8cm圆的面积一半,根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】3.14×8÷2+8
=25.12÷2+8
=12.56+8
=20.56(cm)
3.14×(8÷2)2÷2
=3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(cm2)
一个直径是8cm的半圆形零件,周长是20.56cm,面积是25.12cm2。
10. 6 3
【分析】根据圆的周长公式:周长=π×直径,直径=周长÷π,代入数据,求出直径;直径=半径×2,半径=直径÷2,代入数据,即可解答。
【详解】18.84÷3.14=6(m)
6÷2=3(m)
用一根长为18.84m的绳子围成一个圆,这个圆的直径为6m,半径为3m。
11. 6 12
【分析】根据题意,32个小朋友手拉手围成一个圆圈,则每个小朋友两臂伸平后的长度乘32,即是这个圆圈的周长;
每个小朋友距离靶子的距离,相当于圆的半径;距离最远的两名小朋友之间的距离,相当于圆的直径;
根据圆的周长公式C=πd可知,圆的直径d=C÷π,圆的半径r=d÷2,代入数据计算求解。
【详解】周长:1.2×32=38.4(米)
直径:38.4÷3.14≈12(米)
半径:12÷2=6(米)
每个小朋友距离靶子大约是6米。其中,距离最远的两名小朋友之间的距离是12米。
12. 4 680
【分析】两人相遇时距全程中点20千米,由于甲汽车的速度比乙汽车的速度快,说明相遇时甲比乙多走了20×2=40(千米),根据“相遇时总共多走的千米数÷每小时多走的千米数=相遇时间”可求出相遇时间,再根据“速度和×相遇时间=路程”求全程即可。
【详解】20×2÷(90-80)
=40÷10
=4(小时)
(90+80)×4
=170×4
=680(千米)
相遇时他们各行了4小时,全程长680千米。
【点睛】此题主要考查相遇问题的有关知识,注意“两人相遇时距全程中点20千米”说明快的比慢的多走20×2=40(千米),然后根据“相遇时总共多走的千米数÷每小时多走的千米数=相遇时间”、“速度和×相遇时间=路程”求全程即可。
13.√
【分析】根据圆的周长公式C=2πr,可知圆的半径r=C÷π÷2,即两个圆的周长相等,则它们的半径相等;再根据圆的面积公式S=πr2,可知两个圆的半径相等,那么它们的面积也相等;据此判断。
【详解】如果两个圆的周长相等,则它们的半径相等,那么它们的面积也相等。
原题说法正确。
故答案为:√
14.√
【分析】轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;所以任何一条直径所在的直线都是圆的对称轴,因为圆有无数条直径,所以圆有无数条对称轴。
【详解】根据分析可知,任何一条直径所在的直线都是圆的对称轴,圆有无数条对称轴。原题干说法正确。
故答案为:√
15.×
【分析】根据对称轴的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形。折痕所在的这条直线叫做对称轴,依此作答。
【详解】圆和半圆都是轴对称图形,半圆有1条对称轴,圆有无数条对称轴。
故答案为:×
16.√
【分析】根据圆的周长公式,则大圆周长为,小圆周长为,用大圆周长减小圆周长,化简后即可得解。
【详解】据分析可得,两圆的周长差为:
故答案为:√
17.×
【分析】圆的面积是圆占平面的大小;圆的周长是围成圆的曲线的长度。据此判断。
【详解】圆的面积指的是圆占平面的大小,圆的周长是围成圆的曲线的长度,二者有着本质的区别,所以原题说法错误。
故答案为:×
18.25.74平方厘米
【分析】阴影部分的面积等于一个上底为12厘米,下底为6厘米的梯形的面积减去个半径为6厘米的圆的面积,分别利用梯形和圆的面积公式,求出这两个图形的面积,再相减即可求出阴影部分的面积。
【详解】(12+6)×6÷2-×3.14×62
=18×6÷2-×3.14×36
=54-28.26
=25.74(平方厘米)
即阴影部分的面积是25.74平方厘米。
19.12.56cm;15.7cm
【分析】第一幅图,三角形内角和180°,因此阴影部分的周长可以拼成圆周长的一半,根据圆周长的一半=圆周率×直径÷2,列式计算即可;
第二幅图,阴影部分的周长=直径2cm的圆周长的一半+直径3cm的圆周长的一半+直径(2+3)cm的圆周长的一半,据此列式计算。
【详解】3.14×8÷2=12.56(cm)
3.14×2÷2+3.14×3÷2+3.14×(2+3)÷2
=3.14+4.71+3.14×5÷2
=3.14+4.71+7.85
=15.7(cm)
涂阴影的图形的周长分别是12.56cm、15.7cm。
20.175米
【分析】根据题意,两人第一次相遇时,两人走的路程和是环形跑道一圈的长度,即400米,根据相遇时间=路程和÷速度和,求出相遇时间,再根据路程=速度×时间,求出两人第一次相遇时芳芳走的路程。
【详解】400÷(35+45)
=400÷80
=5(分钟)
35×5=175(米)
答:两人第一次相遇时芳芳走了175米。
【点睛】本题考查了相遇问题,解答本题的关键在于求出两人的相遇时间。
21.40.82平方米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出这个圆形舞池的半径;求增加的面积,就是求圆环的面积;根据圆环的面积公式:面积=π×(大圆的半径2-小圆的半径2),代入数据,即可解答。
【详解】37.68÷3.14÷2
=12÷2
=6(米)
3.14×[(6+1)2-62]
=3.14×[72-36]
=3.14×[49-36]
=3.14×13
=40.82(平方米)
答:舞池面积可增加40.82平方米。
21世纪教育网(www.21cnjy.com)
学校:__________ 姓名:___________ 班级:___________
一、选择题
1.用圆规画一个周长是25.12cm的圆,圆规两脚之间的距离是( )cm。
A.8 B.4 C.2 D.1
2.大圆的半径等于小圆的直径,大圆的周长是小圆的周长的( )。
A.2倍 B. C.4倍 D.
3.用两根长度相等的铁丝分别正好围成一个正方形和一个圆,下列说法中正确的是( )。
A.正方形的面积大 B.圆的面积大 C.它们的面积一样大
4.把一个直径是10cm的圆沿直径分成两个半圆,这两个半圆的周长之和是( )。
A.31.4cm B.41.4cm C.51.4cm D.61.4cm
5.一个圆的周长、直径、半径的和是18.56厘米,这个圆的直径是( )厘米。
A.2 B.3 C.3.14 D.4
二、填空题
6.我国魏晋时期杰出的数学家刘徽得出了较精确的圆周率的值,他采用“( )”一直算到圆内接正192边形,得出圆周率的近似值是3.14。
7.观察下图,你发现了什么?
分析与解答:我们可以把汽车雨刷器看成一条( ),这条( )转动后形成一个( ),这是一个( )图形。
8.已知圆的周长是18.84dm,则这个圆的半径是( )dm。
9.一个直径是8cm的半圆形零件,周长是( )cm,面积是( )cm2。
10.用一根长为18.84m的绳子围成一个圆,这个圆的直径为( )m,半径为( )m。
11.一年级小朋友两臂伸平后长度约是1.2米,32个小朋友手拉手围成一个圆圈做投掷游戏,靶子放在围成的圆圈中心位置,每个小朋友距离靶子大约是( )米。其中,距离最远的两名小朋友之间的距离是( )米。(得数都保留整数)
12.甲、乙两辆汽车同时从A、B两地相向而行,甲汽车每小时行驶90千米,乙汽车每小时行驶80千米,两辆汽车相遇时距离全程中点20千米,则相遇时他们各行了 小时,全程长 千米。
三、判断题
13.如果两个圆的周长相等,那么它们的面积也相等。( )
14.任何一条直径所在的直线都是圆的对称轴,圆有无数条对称轴。( )
15.圆和半圆都是轴对称图形,它们都有无数条对称轴。( )
16.若大圆的直径为d1,小圆的直径为d2,则两圆的周长相差π(d1-d2)。( )
17.圆的面积就是围成圆的曲线的长度。( )
四、计算题
18.求阴影部分的面积。(单位:厘米)
19.我会求下面涂阴影的图形的周长。
五、解答题
20.芳芳和刚刚在学校操场400米的环形跑道上同时同地出发背向而行,芳芳每分钟走35米,刚刚每分钟走45米。两人第一次遇到时芳芳走了多少米?
21.某俱乐部有一个圆形舞池,周长为37.68米,现准备把半径加长1米,舞池面积可增加多少平方米?
21世纪教育网(www.21cnjy.com)
1.B
【分析】画圆时,圆规两脚之间的距离是半径,根据半径=圆的周长÷圆周率÷2,列式计算即可。
【详解】25.12÷3.14÷2=4(cm)
圆规两脚之间的距离是4cm。
故答案为:B
2.A
【分析】根据题意可知,大圆的半径等于小圆的直径;由此可知,大圆的半径等于小圆半径的2倍,设小圆半径为r,则大圆半径为2r,根据圆的周长公式:周长=π×半径×2,分别求出大圆周长和小圆周长,再用大圆周长÷小圆周长,即可解答。
【详解】设小圆半径为r,则大圆半径为2r。
(π×2r×2)÷(πr×2)
=(4πr)÷(2πr)
=2
大圆的半径等于小圆的直径,大圆的周长是小圆的周长的2倍。
故答案为:A
3.B
【分析】设铁丝的长是12.56厘米,根据正方形周长公式:周长=边长×4,边长=周长÷4,代入数据,求出正方形边长;再根据正方形面积公式:面积=边长×边长,求出正方形面积;
根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆的半径,再根据圆的面积公式:面积=π×半径2,代入数据,求出圆的面积,再进行比较,即可解答。
【详解】设铁丝的长是12.56厘米。
正方形边长:12.56÷4=3.14(厘米)
正方形面积:3.14×3.14=9.8596(平方厘米)
圆的半径:
12.56÷3.14÷2
=4÷2
=2(厘米)
圆的面积:
3.14×22
=3.14×4
=12.56(平方厘米)
9.8596<12.56,圆的面积大。
用两根长度相等的铁丝分别正好围成一个正方形和一个圆,圆的面积大。
故答案为:B
4.C
【分析】根据题意,把一个圆沿直径分成两个半圆,根据半圆的周长=圆周长的一半+直径=πd÷2+d,据此求出一个半圆的周长,再乘2,即是这两个半圆的周长之和。
【详解】3.14×10÷2+10
=15.7+10
=25.7(cm)
25.7×2=51.4(cm)
这两个半圆的周长之和是51.4cm。
故答案为:C
5.D
【分析】根据d=2r,C=2πr,可知2r+r+2πr=18.56,根据等式的性质求出r,也就是半径,进而求出直径。
【详解】2r+r+2πr=18.56
解:2r+r+2×3.14×r=18.56
2r+r+6.28r=18.56
9.28r=18.56
r=18.56÷9.28
r=2
2×2=4(厘米)
这个圆的直径是4厘米。
故答案为:D
【点睛】本题主要考查了圆周长公式的灵活应用,要熟练掌握相关公式。
6.割圆术
【详解】通过学习我们知道,圆周率是圆的周长和直径的比值。我国魏晋时期杰出的数学家刘徽得出了较精确的圆周率的值,他采用“割圆术”一直算到圆内接正192边形,得出圆周率的近似值是3.14。
7. 线段 线段 扇形 平面
【详解】由点动成线,线动成面,面动成体可知:我们可以把汽车雨刷器看成一条线段,这条线段转动后形成一个扇形,这是一个平面图形。
8.3
【分析】圆的周长,代入数据求出这个圆的半径即可。
【详解】
(dm)
所以这个圆的半径是3dm。
9. 20.56 25.12
【分析】根据圆的周长公式:周长=π×直径,代入数据,求出直径是8cm的圆的周长,再除以2,求出直径是8cm圆的周长一半,再加上直径的长度,即可求出这个半圆形零件的周长;面积就是直径是8cm圆的面积一半,根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】3.14×8÷2+8
=25.12÷2+8
=12.56+8
=20.56(cm)
3.14×(8÷2)2÷2
=3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(cm2)
一个直径是8cm的半圆形零件,周长是20.56cm,面积是25.12cm2。
10. 6 3
【分析】根据圆的周长公式:周长=π×直径,直径=周长÷π,代入数据,求出直径;直径=半径×2,半径=直径÷2,代入数据,即可解答。
【详解】18.84÷3.14=6(m)
6÷2=3(m)
用一根长为18.84m的绳子围成一个圆,这个圆的直径为6m,半径为3m。
11. 6 12
【分析】根据题意,32个小朋友手拉手围成一个圆圈,则每个小朋友两臂伸平后的长度乘32,即是这个圆圈的周长;
每个小朋友距离靶子的距离,相当于圆的半径;距离最远的两名小朋友之间的距离,相当于圆的直径;
根据圆的周长公式C=πd可知,圆的直径d=C÷π,圆的半径r=d÷2,代入数据计算求解。
【详解】周长:1.2×32=38.4(米)
直径:38.4÷3.14≈12(米)
半径:12÷2=6(米)
每个小朋友距离靶子大约是6米。其中,距离最远的两名小朋友之间的距离是12米。
12. 4 680
【分析】两人相遇时距全程中点20千米,由于甲汽车的速度比乙汽车的速度快,说明相遇时甲比乙多走了20×2=40(千米),根据“相遇时总共多走的千米数÷每小时多走的千米数=相遇时间”可求出相遇时间,再根据“速度和×相遇时间=路程”求全程即可。
【详解】20×2÷(90-80)
=40÷10
=4(小时)
(90+80)×4
=170×4
=680(千米)
相遇时他们各行了4小时,全程长680千米。
【点睛】此题主要考查相遇问题的有关知识,注意“两人相遇时距全程中点20千米”说明快的比慢的多走20×2=40(千米),然后根据“相遇时总共多走的千米数÷每小时多走的千米数=相遇时间”、“速度和×相遇时间=路程”求全程即可。
13.√
【分析】根据圆的周长公式C=2πr,可知圆的半径r=C÷π÷2,即两个圆的周长相等,则它们的半径相等;再根据圆的面积公式S=πr2,可知两个圆的半径相等,那么它们的面积也相等;据此判断。
【详解】如果两个圆的周长相等,则它们的半径相等,那么它们的面积也相等。
原题说法正确。
故答案为:√
14.√
【分析】轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;所以任何一条直径所在的直线都是圆的对称轴,因为圆有无数条直径,所以圆有无数条对称轴。
【详解】根据分析可知,任何一条直径所在的直线都是圆的对称轴,圆有无数条对称轴。原题干说法正确。
故答案为:√
15.×
【分析】根据对称轴的定义:如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形。折痕所在的这条直线叫做对称轴,依此作答。
【详解】圆和半圆都是轴对称图形,半圆有1条对称轴,圆有无数条对称轴。
故答案为:×
16.√
【分析】根据圆的周长公式,则大圆周长为,小圆周长为,用大圆周长减小圆周长,化简后即可得解。
【详解】据分析可得,两圆的周长差为:
故答案为:√
17.×
【分析】圆的面积是圆占平面的大小;圆的周长是围成圆的曲线的长度。据此判断。
【详解】圆的面积指的是圆占平面的大小,圆的周长是围成圆的曲线的长度,二者有着本质的区别,所以原题说法错误。
故答案为:×
18.25.74平方厘米
【分析】阴影部分的面积等于一个上底为12厘米,下底为6厘米的梯形的面积减去个半径为6厘米的圆的面积,分别利用梯形和圆的面积公式,求出这两个图形的面积,再相减即可求出阴影部分的面积。
【详解】(12+6)×6÷2-×3.14×62
=18×6÷2-×3.14×36
=54-28.26
=25.74(平方厘米)
即阴影部分的面积是25.74平方厘米。
19.12.56cm;15.7cm
【分析】第一幅图,三角形内角和180°,因此阴影部分的周长可以拼成圆周长的一半,根据圆周长的一半=圆周率×直径÷2,列式计算即可;
第二幅图,阴影部分的周长=直径2cm的圆周长的一半+直径3cm的圆周长的一半+直径(2+3)cm的圆周长的一半,据此列式计算。
【详解】3.14×8÷2=12.56(cm)
3.14×2÷2+3.14×3÷2+3.14×(2+3)÷2
=3.14+4.71+3.14×5÷2
=3.14+4.71+7.85
=15.7(cm)
涂阴影的图形的周长分别是12.56cm、15.7cm。
20.175米
【分析】根据题意,两人第一次相遇时,两人走的路程和是环形跑道一圈的长度,即400米,根据相遇时间=路程和÷速度和,求出相遇时间,再根据路程=速度×时间,求出两人第一次相遇时芳芳走的路程。
【详解】400÷(35+45)
=400÷80
=5(分钟)
35×5=175(米)
答:两人第一次相遇时芳芳走了175米。
【点睛】本题考查了相遇问题,解答本题的关键在于求出两人的相遇时间。
21.40.82平方米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出这个圆形舞池的半径;求增加的面积,就是求圆环的面积;根据圆环的面积公式:面积=π×(大圆的半径2-小圆的半径2),代入数据,即可解答。
【详解】37.68÷3.14÷2
=12÷2
=6(米)
3.14×[(6+1)2-62]
=3.14×[72-36]
=3.14×[49-36]
=3.14×13
=40.82(平方米)
答:舞池面积可增加40.82平方米。
21世纪教育网(www.21cnjy.com)
