2024-2025学年四川省成都市西川实验中学九年级(上)入学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年四川省成都市西川实验中学九年级(上)入学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 202.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 21:49:44 | ||
图片预览



文档简介
2024-2025学年四川省成都市西川实验中学九年级(上)入学数学试卷
一、选择题:本题共8小题,每小题4分,共32分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.已知关于的方程的一个根为,则实数的值为( )
A. B. C. D.
3.下列因式分解结果正确的是( )
A. B.
C. D.
4.反比例函数的图象经过点,下列各点在此反比例函数图象上的是( )
A. B. C. D.
5.如图,在矩形中,对角线,交于点,,,则的长是( )
A. B. C. D.
6.如图,若点是线段的黄金分割点,,则的长是( )
A. B.
C. D.
7.下列判断错误的是( )
A. 有两组邻边相等的四边形是菱形 B. 有一角为直角的平行四边形是矩形
C. 对角线互相垂直且相等的平行四边形是正方形 D. 矩形的对角线互相平分且相等
8.如图,若设从年到年我国海上风电新增
装机容量的平均增长率为,根据这个统计图可知,应
满足( )
A.
B.
C.
D.
二、填空题:本题共10小题,每小题4分,共40分。
9.已知,则______.
10.若点向上平移个单位后得到的点在轴上,则的值为______.
11.已知关于的一元二次方程有两个相等的实数根,则的值是______.
12.如图,一次函数的图象与反比例函数的图象相交于
点,两点,当时,则自变量的取值范围是______.
13.如图,先将一张正方形纸向上对折、再向左对折,然后沿着图中的虚线剪开,得到两部分,将展开后得到的平面图形是______.
14.若,则的值为______.
15.若关于的分式方程的解为非负数,则的取值范围是______.
16.如图,点,是函数图象上两点,过点作轴,垂足为点,交于点若的面积为,点为的中点,则的值为______.
17.如图,正方形中,点,分别是边,上的两个动点,且正方形的周长是周长的倍.连接,分别与对角线交于点,,给出如下几个结论:若,,则;;若,,则;若,,则其中正确结论的序号为______.
18.如图,在中,,为上一点,且满足,过作交延长线于点,则 ______.
三、解答题:本题共8小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.(10分)计算:
解方程;
.
20.(10分)在如图所示的平面直角坐标系中,的顶点分别为,,.
画出关于点成中心对称的;
在条件下,连接,,四边形的形状是______;
在网格内存在点,使点,,,构成平行四边形,请写出所有符合条件的点的坐标______.
21.(8分)“墙里秋千墙外道,墙外行人,墙里佳人笑”自古以来荡秋千深受孩子们喜爱如图所示,秋千链子的长度为,当摆角恰为时,座板离地面的高度为,当摆动至最高位置时,摆角为,求座板距地面的最大高度为多少?结果精确到;参考数据,,,,,
22.(10分)如图,在中,的平分线交边于点,已知.
求证:;
若,求的度数.
23.(10分)已知:图形上任意一点,图形上任意一点,若点与点之间的距离始终满足,则称图形与图形相离.
已知点,,,.
与直线为相离图形的点是______;
若直线与相离,求的取值范围.
设直线、直线及直线围成的图形为,图形是边长为的正方形,且正方形的各边分别与两坐标轴平行,该正方形对角线的交点坐标为,直接写出图形与图形相离时的取值范围.
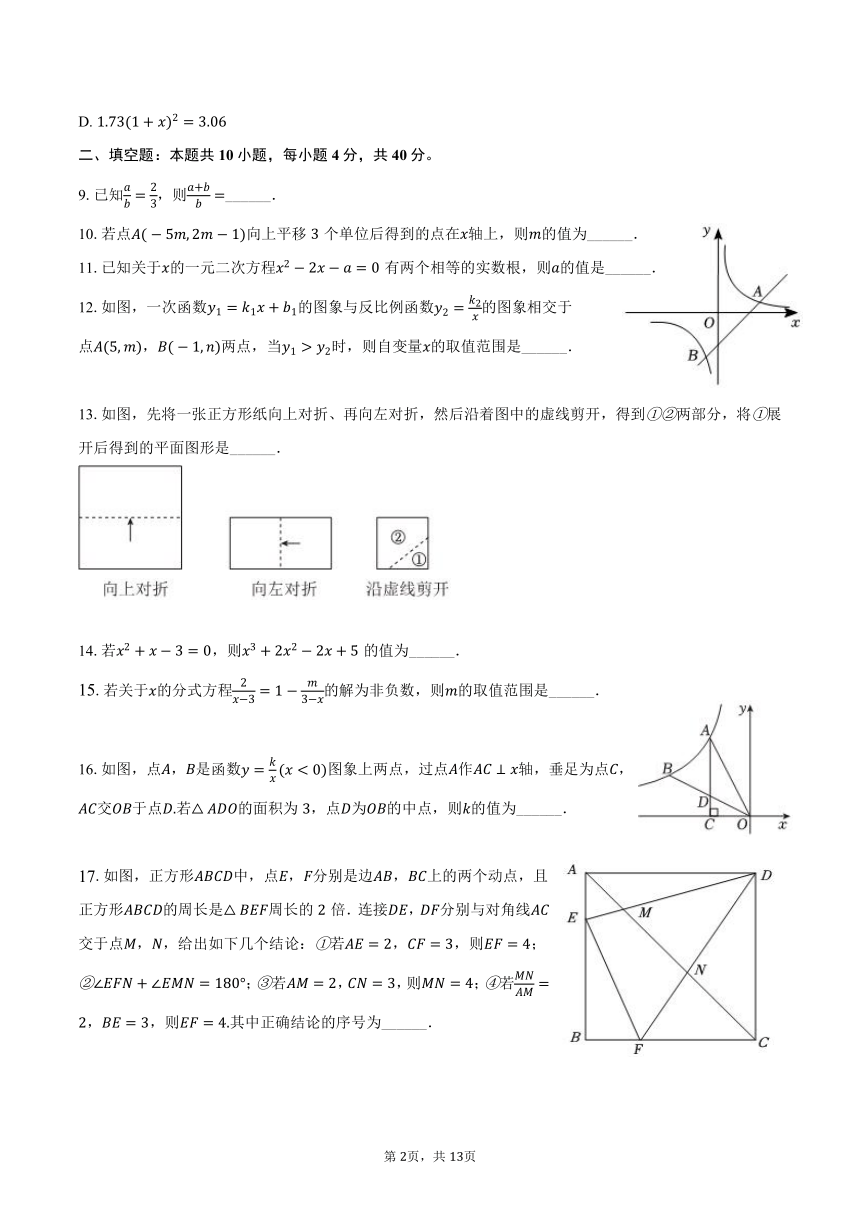
24.(10分)食堂午餐高峰期间,同学们往往需要排队等候购餐经调查发现,每天开餐时,约有人排队,接下来,不断有新的同学进入食堂排队,队列中的同学买到饭后会离开队列食堂目前开放了个售餐窗口规定每人购餐份,每分钟每个窗口能出售午餐份,前分钟每分钟有人进入食堂排队购餐每一天食堂排队等候购餐的人数人与开餐时间分钟的关系如图所示,
求的值.
求开餐到第分钟时食堂排队购餐等候的人数.
若要在开始售餐分钟内让所有的排队的学生都能买到,以便后来到同学随到随购,至少需要同时开放几个窗口?
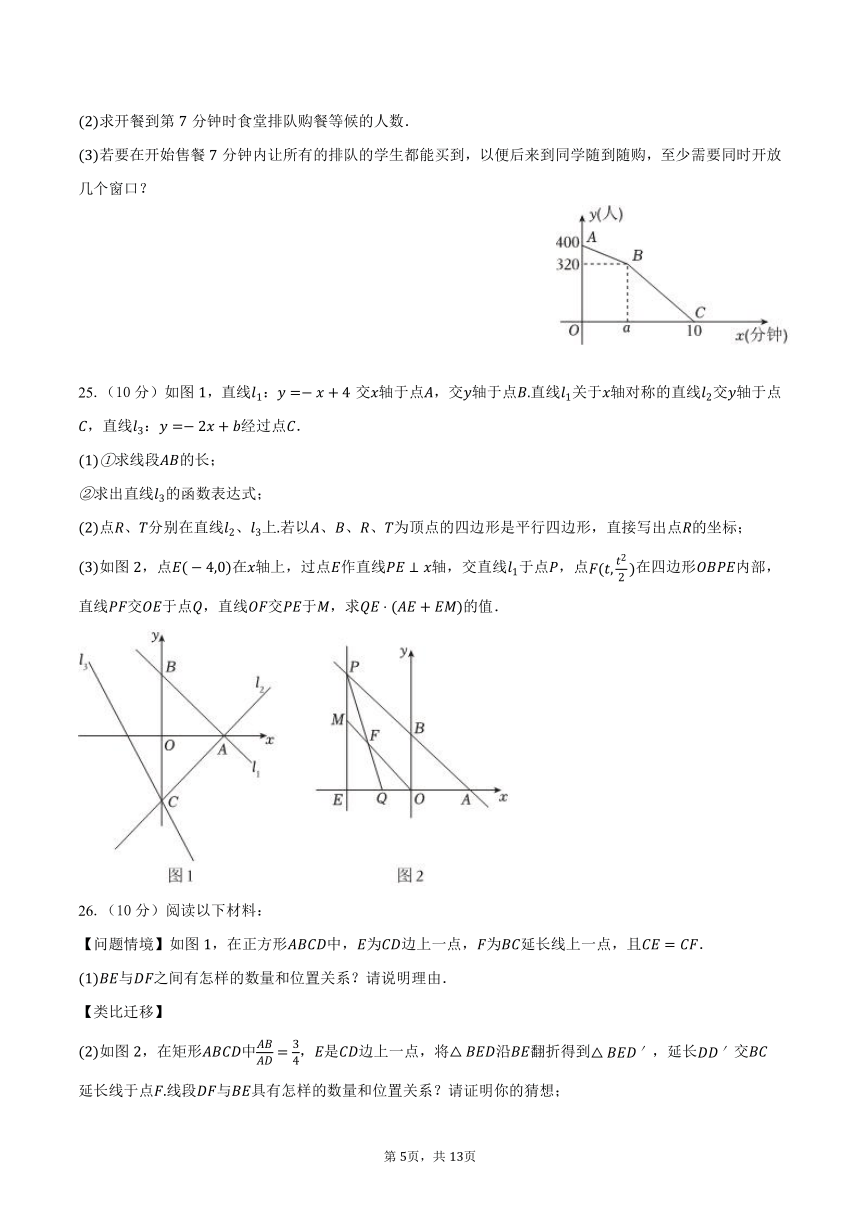
25.(10分)如图,直线:交轴于点,交轴于点直线关于轴对称的直线交轴于点,直线:经过点.
求线段的长;
求出直线的函数表达式;
点、分别在直线、上若以、、、为顶点的四边形是平行四边形,直接写出点的坐标;
如图,点在轴上,过点作直线轴,交直线于点,点在四边形内部,直线交于点,直线交于,求的值.
26.(10分)阅读以下材料:
【问题情境】如图,在正方形中,为边上一点,为延长线上一点,且.
与之间有怎样的数量和位置关系?请说明理由.
【类比迁移】
如图,在矩形中,是边上一点,将沿翻折得到,延长交延长线于点线段与具有怎样的数量和位置关系?请证明你的猜想;
【拓展提升】
如图,在菱形中,,,是上一点,绕点顺时针旋转得,绕点顺时针旋转得,当时,求四边形的面积.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或
13.菱形
14.
15.且
16.
17.
18.
19.解:去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化为,得,
检验:当时,,则为原方程的增根,
所以原方程无解;
原式
.
20.如图,即为所求.
与关于点成中心对称,
,,
四边形为平行四边形.
如图,点,均符合条件,
符合条件的点的坐标为或.
21.解:过点作,垂足为,过点作,垂足为,
由题意得:,,
在中,,
,
在中,,
,
,
座板距地面的最大高度约为.
22.证明:平分,
,
,
,
,
∽,
,
.
解:∽,
,
,
,
,
,,
,
,,,
,
是直角三角形,且,
的度数是.
23.,;
当直线过点时,
,
解得:.
当直线过点时,
,
解得:.
的取值范围是或.
如图所示:
图形与图形相离时的取值范围是或或.
24.解:根据“等候购餐的人数开餐时排队人数前分钟新增排队人数购餐后离开的人数”,得,
解得,
的值是.
当时,设排队等候购餐的人数与开餐时间的关系为、为常数,且.
将坐标和代入,
得,
解得,
.
当时,,
开餐到第分钟时食堂排队购餐等候人;
设同时开放个窗口,则,解得,
所以至少需同时开放个售票窗口.
25.解:直线:交轴于点,交轴于点,
则点、的坐标分别为:、,
则;
直线关于轴对称的直线交轴于点,
则点,则,
则直线的表达式为:;
设点、的坐标分别为:、,
当为对角线时,由中点坐标公式得:
,解得:,
则点的坐标为:;
当、为对角线时,
同理可得:或,
解得:或,
则点的坐标为:或;
则点的坐标为:或或;
由点、的坐标得,直线的表达式为:,
令,则,
则,
同理可得:点,
则,
而,
则.
26.解:,,理由如下,如图,
延长交于点,
四边形为正方形,
,,
,
≌,
,,
在和中,
,
,即;
,,理由如图下,如图,延长交于,
由折叠得,点与点关于对称,
,即,
,
在和中,
,
,
,
∽,
:::,即;
如图,连接并延长交于点,交于,过作于,交的延长线于,
由旋转得,,,,
,
≌,
,
,
在和中,
,
,
,
,
,,
,,
,
,
,
,
,
,,
,,
,
,
,
,
∽,
::,即::,
,
,
.
第1页,共1页
一、选择题:本题共8小题,每小题4分,共32分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.已知关于的方程的一个根为,则实数的值为( )
A. B. C. D.
3.下列因式分解结果正确的是( )
A. B.
C. D.
4.反比例函数的图象经过点,下列各点在此反比例函数图象上的是( )
A. B. C. D.
5.如图,在矩形中,对角线,交于点,,,则的长是( )
A. B. C. D.
6.如图,若点是线段的黄金分割点,,则的长是( )
A. B.
C. D.
7.下列判断错误的是( )
A. 有两组邻边相等的四边形是菱形 B. 有一角为直角的平行四边形是矩形
C. 对角线互相垂直且相等的平行四边形是正方形 D. 矩形的对角线互相平分且相等
8.如图,若设从年到年我国海上风电新增
装机容量的平均增长率为,根据这个统计图可知,应
满足( )
A.
B.
C.
D.
二、填空题:本题共10小题,每小题4分,共40分。
9.已知,则______.
10.若点向上平移个单位后得到的点在轴上,则的值为______.
11.已知关于的一元二次方程有两个相等的实数根,则的值是______.
12.如图,一次函数的图象与反比例函数的图象相交于
点,两点,当时,则自变量的取值范围是______.
13.如图,先将一张正方形纸向上对折、再向左对折,然后沿着图中的虚线剪开,得到两部分,将展开后得到的平面图形是______.
14.若,则的值为______.
15.若关于的分式方程的解为非负数,则的取值范围是______.
16.如图,点,是函数图象上两点,过点作轴,垂足为点,交于点若的面积为,点为的中点,则的值为______.
17.如图,正方形中,点,分别是边,上的两个动点,且正方形的周长是周长的倍.连接,分别与对角线交于点,,给出如下几个结论:若,,则;;若,,则;若,,则其中正确结论的序号为______.
18.如图,在中,,为上一点,且满足,过作交延长线于点,则 ______.
三、解答题:本题共8小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.(10分)计算:
解方程;
.
20.(10分)在如图所示的平面直角坐标系中,的顶点分别为,,.
画出关于点成中心对称的;
在条件下,连接,,四边形的形状是______;
在网格内存在点,使点,,,构成平行四边形,请写出所有符合条件的点的坐标______.
21.(8分)“墙里秋千墙外道,墙外行人,墙里佳人笑”自古以来荡秋千深受孩子们喜爱如图所示,秋千链子的长度为,当摆角恰为时,座板离地面的高度为,当摆动至最高位置时,摆角为,求座板距地面的最大高度为多少?结果精确到;参考数据,,,,,
22.(10分)如图,在中,的平分线交边于点,已知.
求证:;
若,求的度数.
23.(10分)已知:图形上任意一点,图形上任意一点,若点与点之间的距离始终满足,则称图形与图形相离.
已知点,,,.
与直线为相离图形的点是______;
若直线与相离,求的取值范围.
设直线、直线及直线围成的图形为,图形是边长为的正方形,且正方形的各边分别与两坐标轴平行,该正方形对角线的交点坐标为,直接写出图形与图形相离时的取值范围.
24.(10分)食堂午餐高峰期间,同学们往往需要排队等候购餐经调查发现,每天开餐时,约有人排队,接下来,不断有新的同学进入食堂排队,队列中的同学买到饭后会离开队列食堂目前开放了个售餐窗口规定每人购餐份,每分钟每个窗口能出售午餐份,前分钟每分钟有人进入食堂排队购餐每一天食堂排队等候购餐的人数人与开餐时间分钟的关系如图所示,
求的值.
求开餐到第分钟时食堂排队购餐等候的人数.
若要在开始售餐分钟内让所有的排队的学生都能买到,以便后来到同学随到随购,至少需要同时开放几个窗口?
25.(10分)如图,直线:交轴于点,交轴于点直线关于轴对称的直线交轴于点,直线:经过点.
求线段的长;
求出直线的函数表达式;
点、分别在直线、上若以、、、为顶点的四边形是平行四边形,直接写出点的坐标;
如图,点在轴上,过点作直线轴,交直线于点,点在四边形内部,直线交于点,直线交于,求的值.
26.(10分)阅读以下材料:
【问题情境】如图,在正方形中,为边上一点,为延长线上一点,且.
与之间有怎样的数量和位置关系?请说明理由.
【类比迁移】
如图,在矩形中,是边上一点,将沿翻折得到,延长交延长线于点线段与具有怎样的数量和位置关系?请证明你的猜想;
【拓展提升】
如图,在菱形中,,,是上一点,绕点顺时针旋转得,绕点顺时针旋转得,当时,求四边形的面积.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或
13.菱形
14.
15.且
16.
17.
18.
19.解:去分母,得,
去括号,得,
移项,得,
合并同类项,得,
系数化为,得,
检验:当时,,则为原方程的增根,
所以原方程无解;
原式
.
20.如图,即为所求.
与关于点成中心对称,
,,
四边形为平行四边形.
如图,点,均符合条件,
符合条件的点的坐标为或.
21.解:过点作,垂足为,过点作,垂足为,
由题意得:,,
在中,,
,
在中,,
,
,
座板距地面的最大高度约为.
22.证明:平分,
,
,
,
,
∽,
,
.
解:∽,
,
,
,
,
,,
,
,,,
,
是直角三角形,且,
的度数是.
23.,;
当直线过点时,
,
解得:.
当直线过点时,
,
解得:.
的取值范围是或.
如图所示:
图形与图形相离时的取值范围是或或.
24.解:根据“等候购餐的人数开餐时排队人数前分钟新增排队人数购餐后离开的人数”,得,
解得,
的值是.
当时,设排队等候购餐的人数与开餐时间的关系为、为常数,且.
将坐标和代入,
得,
解得,
.
当时,,
开餐到第分钟时食堂排队购餐等候人;
设同时开放个窗口,则,解得,
所以至少需同时开放个售票窗口.
25.解:直线:交轴于点,交轴于点,
则点、的坐标分别为:、,
则;
直线关于轴对称的直线交轴于点,
则点,则,
则直线的表达式为:;
设点、的坐标分别为:、,
当为对角线时,由中点坐标公式得:
,解得:,
则点的坐标为:;
当、为对角线时,
同理可得:或,
解得:或,
则点的坐标为:或;
则点的坐标为:或或;
由点、的坐标得,直线的表达式为:,
令,则,
则,
同理可得:点,
则,
而,
则.
26.解:,,理由如下,如图,
延长交于点,
四边形为正方形,
,,
,
≌,
,,
在和中,
,
,即;
,,理由如图下,如图,延长交于,
由折叠得,点与点关于对称,
,即,
,
在和中,
,
,
,
∽,
:::,即;
如图,连接并延长交于点,交于,过作于,交的延长线于,
由旋转得,,,,
,
≌,
,
,
在和中,
,
,
,
,
,,
,,
,
,
,
,
,
,,
,,
,
,
,
,
∽,
::,即::,
,
,
.
第1页,共1页
同课章节目录
