2024-2025学年安徽省安庆市多校联考九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年安徽省安庆市多校联考九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 96.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-15 22:47:27 | ||
图片预览



文档简介
2024-2025学年安徽省安庆市多校联考九年级(上)开学数学试卷
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若,则( )
A. B. C. D.
2.若关于的一元二次方程有两个不相等的实数根,则的值可能为( )
A. B. C. D.
3.一个多边形的内角和是它的外角和的倍,则这个多边形的边数是( )
A. B. C. D.
4.小明根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数 中位数 众数 方差
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
5.如图,菱形的对角线,交于点若,,则菱形的周长是( )
A.
B.
C.
D.
6.在下列条件中,不是直角三角形的是( )
A. B. ::::
C. D. ::::
7.实数,在数轴上的位置如图所示,化简的结果是( )
A. B. C. D.
8.将一对直角三角板如图放置,点在的延长线上,点在上,,,,,,则的长度是( )
A. B.
C. D.
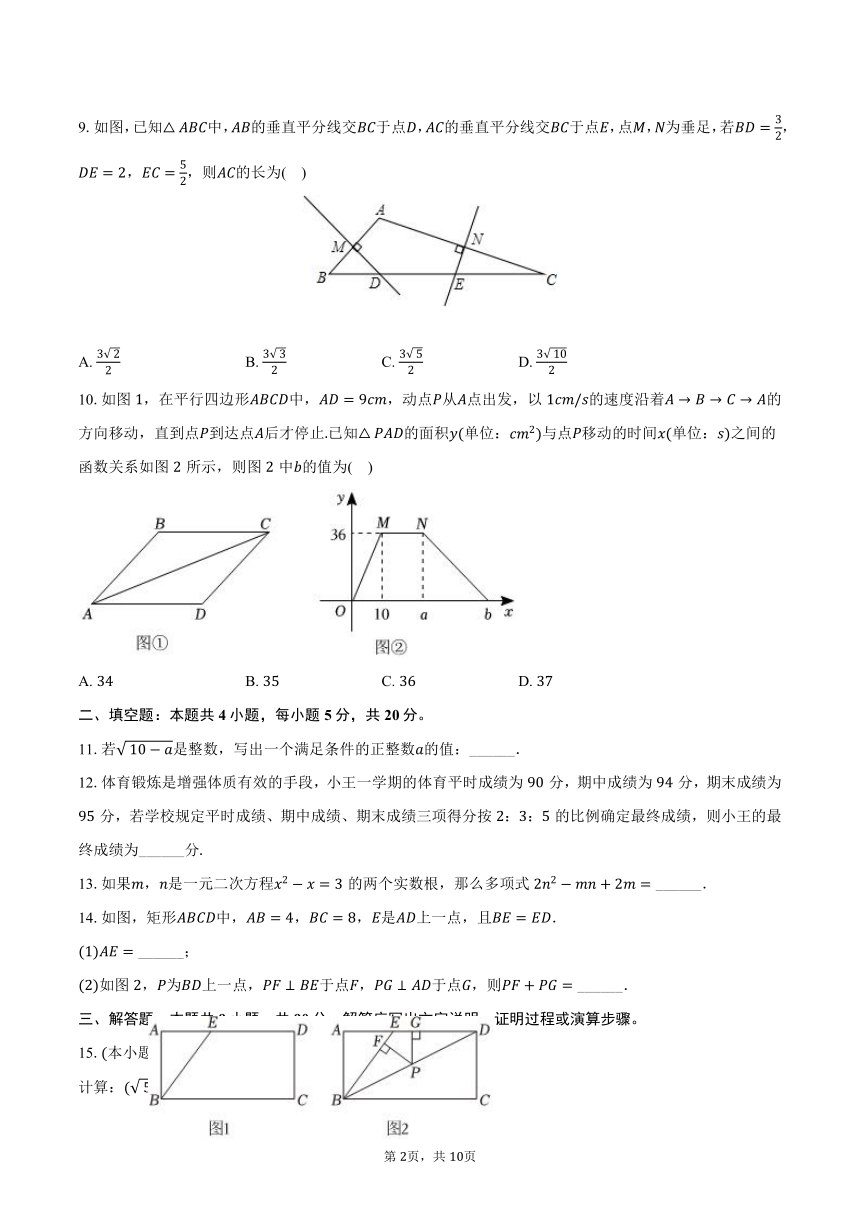
9.如图,已知中,的垂直平分线交于点,的垂直平分线交于点,点,为垂足,若,,,则的长为( )
A. B. C. D.
10.如图,在平行四边形中,,动点从点出发,以的速度沿着的方向移动,直到点到达点后才停止已知的面积单位:与点移动的时间单位:之间的函数关系如图所示,则图中的值为( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分。
11.若是整数,写出一个满足条件的正整数的值:______.
12.体育锻炼是增强体质有效的手段,小王一学期的体育平时成绩为分,期中成绩为分,期末成绩为分,若学校规定平时成绩、期中成绩、期末成绩三项得分按::的比例确定最终成绩,则小王的最终成绩为______分
13.如果,是一元二次方程的两个实数根,那么多项式 ______.
14.如图,矩形中,,,是上一点,且.
______;
如图,为上一点,于点,于点,则 ______.
三、解答题:本题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:.
16.本小题分
已知:如图,在中,中线,交于点,,分别是,的中点连接、、、,求证:.
17.本小题分
某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地阴影部分如图,已知,,,,技术人员通过测量确定了.
小区内部分居民每天必须从点经过点再到点位置,为了方便居民出入,技术人员打算在绿地中开辟一条从点直通点的小路,请问如果方案落实施工完成,居民从点到点将少走多少路程?
这片绿地的面积是多少?
18.本小题分
如图,在矩形中,延长到,使,延长到,使,连接、、、.
求证:四边形是菱形;
若,,求菱形的面积.
19.本小题分
年月日,神舟十八号载人飞船发射取得成功,将我国航天事业推向了新的高峰南沙区某中学为了丰富学生们航天知识,组织全校学生进行航天知识竞赛,并随机抽取名学生的成绩,整理成如统计表:
分数
频数
该名同学这次竞赛成绩的中位数是______.
求该名同学这次竞赛成绩的平均数.
若竞赛成绩分以上含分为优秀,该校有名学生,请估计竞赛成绩为优秀的人数.
20.本小题分
已知关于的方程.
求证:无论为何值,方程总有实数根;
若方程的两个实数根为,,求代数式的值.
21.本小题分
嘉嘉根据学习“数与式”积累的活动经验,想通过“特殊到一般”的方法探究二次根式的运算规律下面是嘉嘉的探究过程:
等式:;等式:;
等式:;等式;______
【特例探究】将题目中的横线处补充完整;
【归纳猜想】若为正整数,用含的代数式表示上述运算规律,并证明此规律成立;
【应用规律】嘉嘉写出一个等式均为正整数,若该等式符合上述规律,则的值为______.
22.本小题分
综合实践用矩形硬纸片制作无盖纸盒如图,有一张长,宽的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图所示的无盖纸盒硬纸片厚度忽略不计
若剪去的正方形的边长为,则纸盒底面长方形的长为______,宽为______;
若纸盒的底面积为,请计算剪去的正方形的边长;
如图,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形阴影部分,经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
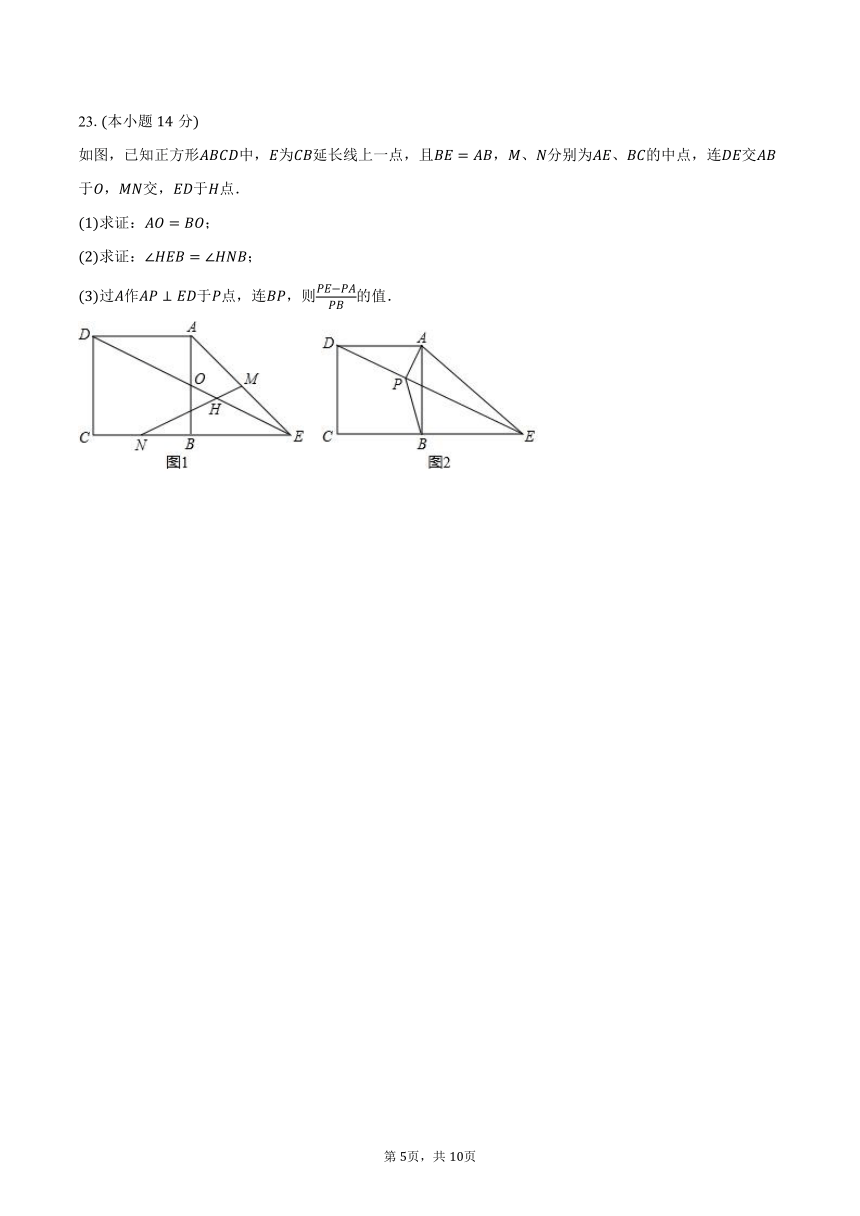
23.本小题分
如图,已知正方形中,为延长线上一点,且,、分别为、的中点,连交于,交,于点.
求证:;
求证:;
过作于点,连,则的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.答案不唯一
12.
13.
14.
15.解:原式
.
16.证明:,都是的中线,
是的中位线,
,,
,分别是,的中点,
,,
且,
四边形是平行四边形,
.
17.解:如图,连接,
,,,
,
,
答:居民从点到点将少走路程;
,,
:
是直角三角形,,
,,
,
答:这片绿地的面积是.
18.证明:四边形是矩形,
,
,即,
,,
四边形是平行四边形,
平行四边形是菱形.
解:四边形是菱形,,
,
,,
,
,
,,
.
19.;
该名同学这次竞赛成绩的平均数为;
名,
答:估计竞赛成绩为优秀的人数为名.
20.证明:
,
,
,
该方程总有两个实数根;
解:该方程的两个实数根为,,
,,
.
21.;
根据规律,用含的式子表示为:,
证明:等式左边
右边;
.
22.,;
设剪去的正方形的边长为,
根据题意得:,
解得:不符合题意,舍去,,
答:剪去的正方形的边长为;
设剪去的正方形的边长为,
根据题意得:,
解得:不符合题意,舍去,,
答:剪去的正方形的边长为.
23.证明:四边形是正方形,
,,
,,
,
,
≌,
;
证明:延长至,且使,连接、,如图所示:
则,
四边形是矩形,
,,,
在和中,,
≌,
,
,,
为的中点,
为的中位线,
,
;
解:过点作交于,如图所示:
则,
,
,
,
,
,,
由角的互余关系得:,
,
在和中,,
≌,
,,
是等腰直角三角形,
,
.
第1页,共1页
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若,则( )
A. B. C. D.
2.若关于的一元二次方程有两个不相等的实数根,则的值可能为( )
A. B. C. D.
3.一个多边形的内角和是它的外角和的倍,则这个多边形的边数是( )
A. B. C. D.
4.小明根据演讲比赛中九位评委所给的分数制作了如下表格:
平均数 中位数 众数 方差
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
5.如图,菱形的对角线,交于点若,,则菱形的周长是( )
A.
B.
C.
D.
6.在下列条件中,不是直角三角形的是( )
A. B. ::::
C. D. ::::
7.实数,在数轴上的位置如图所示,化简的结果是( )
A. B. C. D.
8.将一对直角三角板如图放置,点在的延长线上,点在上,,,,,,则的长度是( )
A. B.
C. D.
9.如图,已知中,的垂直平分线交于点,的垂直平分线交于点,点,为垂足,若,,,则的长为( )
A. B. C. D.
10.如图,在平行四边形中,,动点从点出发,以的速度沿着的方向移动,直到点到达点后才停止已知的面积单位:与点移动的时间单位:之间的函数关系如图所示,则图中的值为( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分。
11.若是整数,写出一个满足条件的正整数的值:______.
12.体育锻炼是增强体质有效的手段,小王一学期的体育平时成绩为分,期中成绩为分,期末成绩为分,若学校规定平时成绩、期中成绩、期末成绩三项得分按::的比例确定最终成绩,则小王的最终成绩为______分
13.如果,是一元二次方程的两个实数根,那么多项式 ______.
14.如图,矩形中,,,是上一点,且.
______;
如图,为上一点,于点,于点,则 ______.
三、解答题:本题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:.
16.本小题分
已知:如图,在中,中线,交于点,,分别是,的中点连接、、、,求证:.
17.本小题分
某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角建造了一块绿化地阴影部分如图,已知,,,,技术人员通过测量确定了.
小区内部分居民每天必须从点经过点再到点位置,为了方便居民出入,技术人员打算在绿地中开辟一条从点直通点的小路,请问如果方案落实施工完成,居民从点到点将少走多少路程?
这片绿地的面积是多少?
18.本小题分
如图,在矩形中,延长到,使,延长到,使,连接、、、.
求证:四边形是菱形;
若,,求菱形的面积.
19.本小题分
年月日,神舟十八号载人飞船发射取得成功,将我国航天事业推向了新的高峰南沙区某中学为了丰富学生们航天知识,组织全校学生进行航天知识竞赛,并随机抽取名学生的成绩,整理成如统计表:
分数
频数
该名同学这次竞赛成绩的中位数是______.
求该名同学这次竞赛成绩的平均数.
若竞赛成绩分以上含分为优秀,该校有名学生,请估计竞赛成绩为优秀的人数.
20.本小题分
已知关于的方程.
求证:无论为何值,方程总有实数根;
若方程的两个实数根为,,求代数式的值.
21.本小题分
嘉嘉根据学习“数与式”积累的活动经验,想通过“特殊到一般”的方法探究二次根式的运算规律下面是嘉嘉的探究过程:
等式:;等式:;
等式:;等式;______
【特例探究】将题目中的横线处补充完整;
【归纳猜想】若为正整数,用含的代数式表示上述运算规律,并证明此规律成立;
【应用规律】嘉嘉写出一个等式均为正整数,若该等式符合上述规律,则的值为______.
22.本小题分
综合实践用矩形硬纸片制作无盖纸盒如图,有一张长,宽的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图所示的无盖纸盒硬纸片厚度忽略不计
若剪去的正方形的边长为,则纸盒底面长方形的长为______,宽为______;
若纸盒的底面积为,请计算剪去的正方形的边长;
如图,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形阴影部分,经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
23.本小题分
如图,已知正方形中,为延长线上一点,且,、分别为、的中点,连交于,交,于点.
求证:;
求证:;
过作于点,连,则的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.答案不唯一
12.
13.
14.
15.解:原式
.
16.证明:,都是的中线,
是的中位线,
,,
,分别是,的中点,
,,
且,
四边形是平行四边形,
.
17.解:如图,连接,
,,,
,
,
答:居民从点到点将少走路程;
,,
:
是直角三角形,,
,,
,
答:这片绿地的面积是.
18.证明:四边形是矩形,
,
,即,
,,
四边形是平行四边形,
平行四边形是菱形.
解:四边形是菱形,,
,
,,
,
,
,,
.
19.;
该名同学这次竞赛成绩的平均数为;
名,
答:估计竞赛成绩为优秀的人数为名.
20.证明:
,
,
,
该方程总有两个实数根;
解:该方程的两个实数根为,,
,,
.
21.;
根据规律,用含的式子表示为:,
证明:等式左边
右边;
.
22.,;
设剪去的正方形的边长为,
根据题意得:,
解得:不符合题意,舍去,,
答:剪去的正方形的边长为;
设剪去的正方形的边长为,
根据题意得:,
解得:不符合题意,舍去,,
答:剪去的正方形的边长为.
23.证明:四边形是正方形,
,,
,,
,
,
≌,
;
证明:延长至,且使,连接、,如图所示:
则,
四边形是矩形,
,,,
在和中,,
≌,
,
,,
为的中点,
为的中位线,
,
;
解:过点作交于,如图所示:
则,
,
,
,
,
,,
由角的互余关系得:,
,
在和中,,
≌,
,,
是等腰直角三角形,
,
.
第1页,共1页
同课章节目录
