人教版2024-2025学年六年级数学上册第二单元位置与方向(二)思维素养篇【从课堂到奥数】(原卷版+解析)
文档属性
| 名称 | 人教版2024-2025学年六年级数学上册第二单元位置与方向(二)思维素养篇【从课堂到奥数】(原卷版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-16 09:21:59 | ||
图片预览


文档简介
目 录
【课内精选一】确定物体的位置。 3
【课内精选二】数对与位置。 4
【课内精选三】描述并绘制路线图。 5
【奥数拓展一】在图形中确定物体的位置。 6
【奥数拓展二】数对与位置综合应用。 7
【奥数拓展三】描述并绘制路线图。 8
【奥数拓展四】数列与位置。 9
【奥数拓展五】方格游戏。 10
第二单元位置与方向(二)思维素养篇【从课堂到奥数】
【课内精选一】确定物体的位置。
看图,填一填。以学校为观测点。
(1)小青家在学校( )方向( )米处。
(2)小华家在学校( )偏( )( )°的方向上。
(3)商店在学校( )方向( )米处。
(4)小红家在学校( )偏( )( )°的方向上。
(5)汽车站在学校( )方向( )米处。
【专项训练】
量一量,填一填。
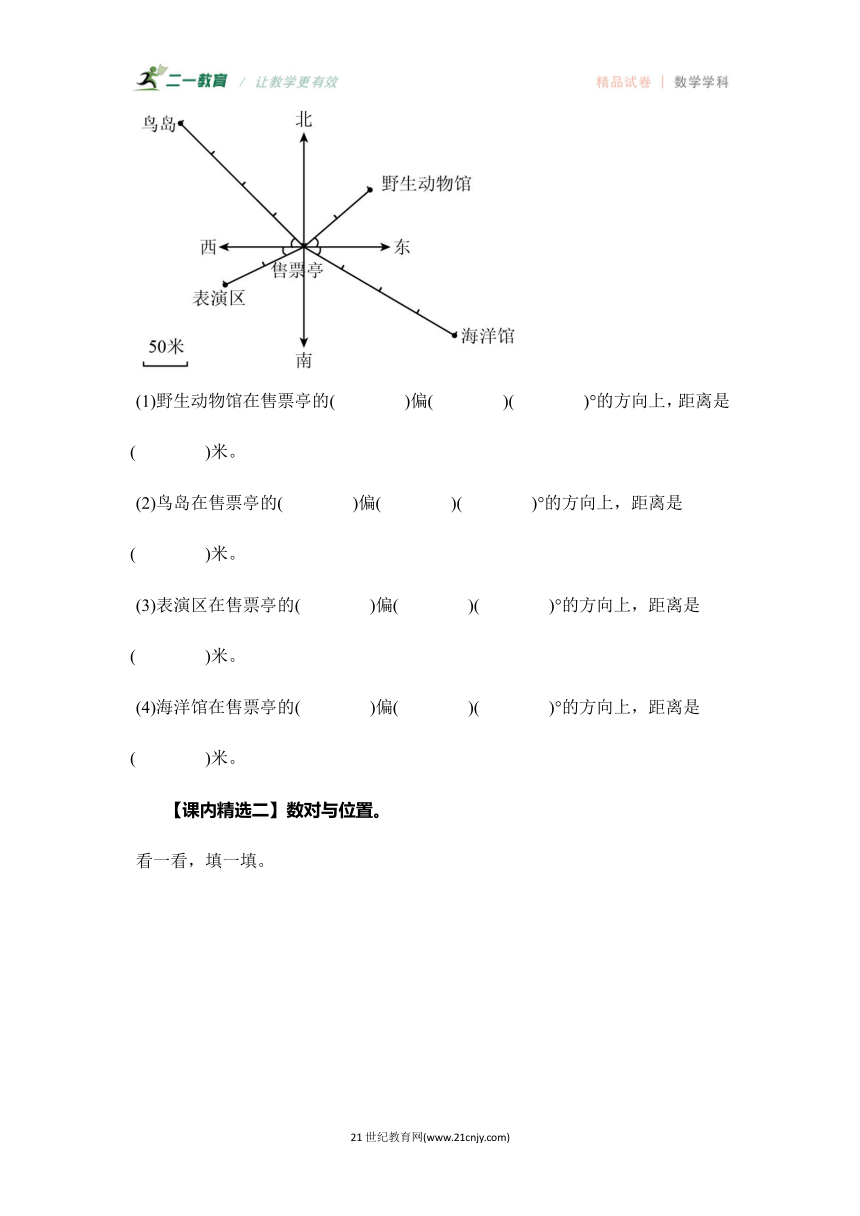
(1)野生动物馆在售票亭的( )偏( )( )°的方向上,距离是( )米。
(2)鸟岛在售票亭的( )偏( )( )°的方向上,距离是( )米。
(3)表演区在售票亭的( )偏( )( )°的方向上,距离是( )米。
(4)海洋馆在售票亭的( )偏( )( )°的方向上,距离是( )米。
【课内精选二】数对与位置。
看一看,填一填。
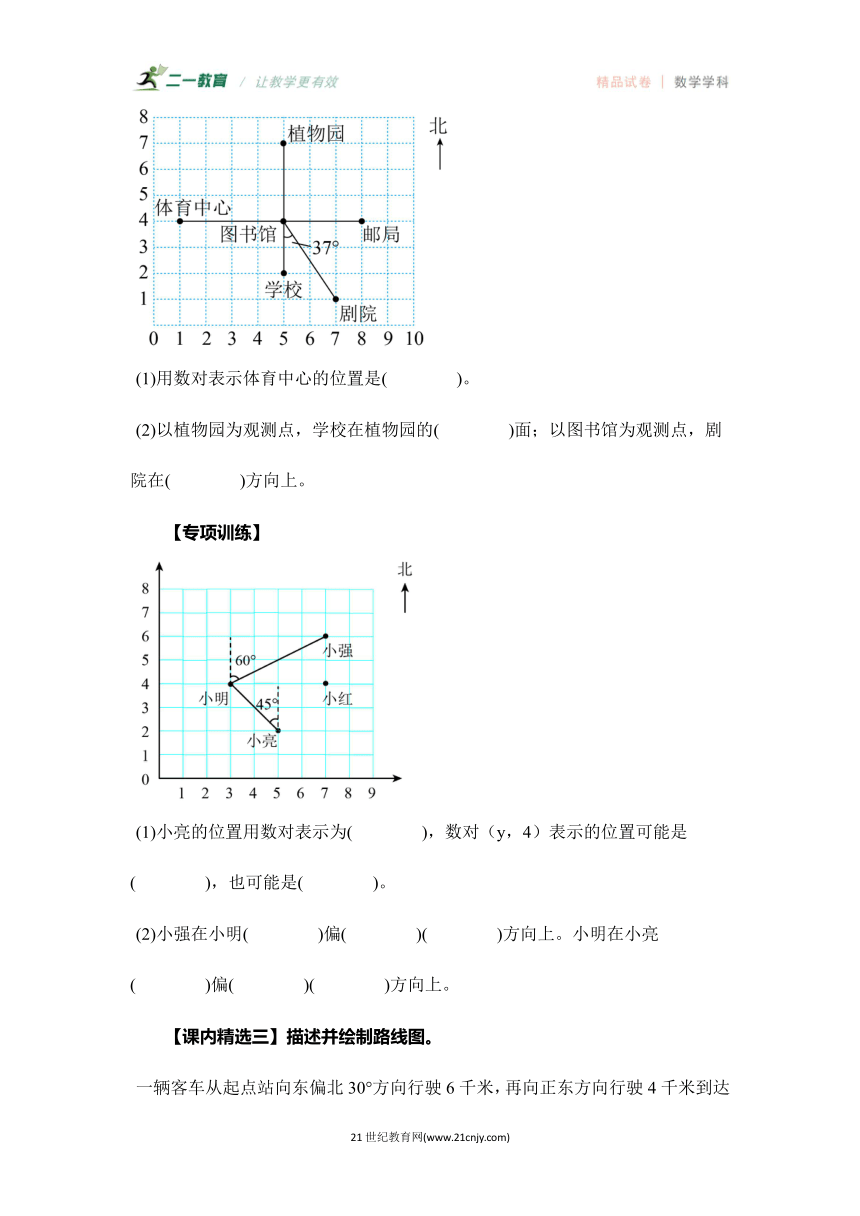
(1)用数对表示体育中心的位置是( )。
(2)以植物园为观测点,学校在植物园的( )面;以图书馆为观测点,剧院在( )方向上。
【专项训练】
(1)小亮的位置用数对表示为( ),数对(y,4)表示的位置可能是( ),也可能是( )。
(2)小强在小明( )偏( )( )方向上。小明在小亮( )偏( )( )方向上。
【课内精选三】描述并绘制路线图。
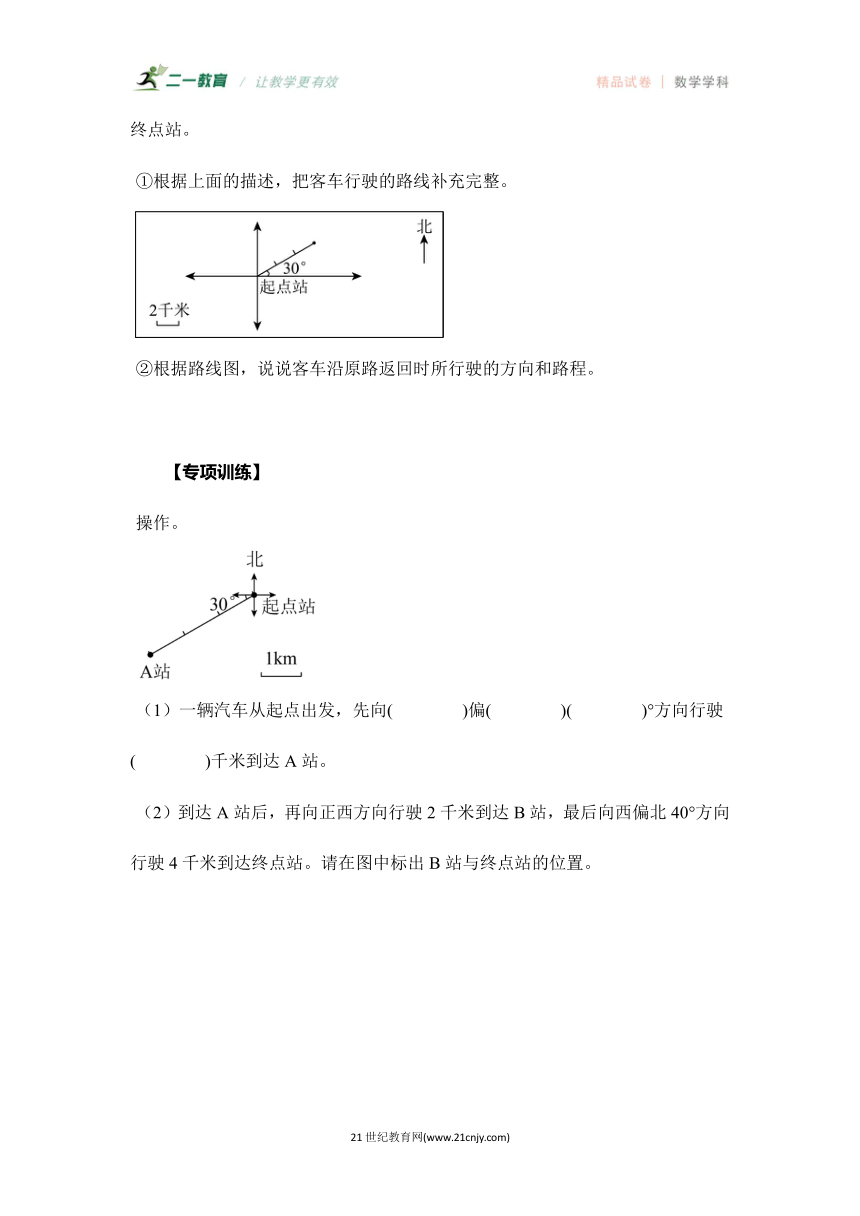
一辆客车从起点站向东偏北30°方向行驶6千米,再向正东方向行驶4千米到达终点站。
①根据上面的描述,把客车行驶的路线补充完整。
②根据路线图,说说客车沿原路返回时所行驶的方向和路程。
【专项训练】
操作。
(1)一辆汽车从起点出发,先向( )偏( )( )°方向行驶( )千米到达A站。
(2)到达A站后,再向正西方向行驶2千米到达B站,最后向西偏北40°方向行驶4千米到达终点站。请在图中标出B站与终点站的位置。
【奥数拓展一】在图形中确定物体的位置。
图中三角形ABC是等腰三角形。已知∠2=40°,AC=BC。点B在点C的( )方向上,点A在点C的东偏北( )°方向上。
【专项训练】
已知下图中每个方格的边长是1厘米,三角形ABC是一个等边三角形,那么,点C在点A的( )偏( ) ( )°方向( )厘米处。
【奥数拓展二】数对与位置综合应用。
看图填空。
(1)如果A点的位置用数对(1,2)表示,那么B点的位置可用数对( )表示。
(2)如果一个小正方形的对角线长10米,点C在点B的南偏东45度方向20米处,请在图上标出C点;点D在A点的东偏南45度方向20米处,请在图上标出D点。
(3)连接ABCD四点,再画出将四边形ABCD向右平移3格后的图形。
【专项训练】
曾正同学是个数学迷。他在一张纸上画了10×10的方格用以研究有关图形的数学问题,假定一个方格的对角线长代表10m,所研究的点都是网格的交点。
(1)点(0,0)北偏东45°方向30m是点A,它的位置用数对表示是( )。
(2)点A北偏西45方向20m是点B,点B北偏东45°方向20m是点C,点C南偏东45°方向20m是点D。用A、B、C、D四个点顺次连接围成一个四边形,它的面积是多少?
(3)请你设计不同于点D的另一个点E使得以A、B、C、E为端点的线段围成四边形的面积与第(2)题用A、B、C、D四个点顺次连接所围成的四边形面积相等。点E可以有不同的设计,这样的点共有( )个,写出其中的四个点E:( )、( )、( )、( )。
【奥数拓展三】描述并绘制路线图。
如图是芳芳每天从家到学校的路线图。
(1)根据路线图把表格中的数据补充完整。
路线 方向 路程 时间
家→超市 5分钟
超市→医院 10分钟
医院→学校 9分钟
(2)芳芳每天从家出发到学校走多少米?平均每分钟走多少米?
【专项训练】
小华从家出发,先向东走200米到达A地,再向东偏北45°方向行500米到达B地,最后向西偏北30°方向行300米到达终点C地。
(1)根据上面的描述,把小华走的路线图画完整。
(2)如果从终点C原路返回家里用了12分30秒,那么他返回时每分钟行多少米?
【奥数拓展四】数列与位置。
已知数列,,…,则第10个数是( )。
【专项训练】
1.找规律、1、、、、…,这串数中第7个数是( )。
2.一列分数: 、、、、、、…,按规律,是这列分数中的第( )个。
3.瑞士数学教师巴尔末成功地从光谱数据,……中得到巴尔末公式,从而打开了光谱奥妙的大门。按这种规律写出的第5个数是( ),第8个数是( )。
【奥数拓展五】方格游戏。
“扫雷”是一款经典的益智游戏,规则如下:
①图中阴影部分是雷区,共有10个雷;
②方格中的数字表示这个方格周围雷的个数。
例如:左图中标有“★”的方格周围有8个方格(标数的方格)。
请你根据上面的例图,完成下图。(是雷的标○,不是雷的标×)
【专项训练】
1.如图,每个小方块周围最多有8个小方块,外围没标数字的小方块是未探明的雷区,其中每个小方块最多有一个雷。内部的小方块没有雷,数字表示所在小方块周围的雷数。图中共有( )个雷。
2.下面是找笑脸游戏,规则是:点开的方格中的数是几,就表示围着它的方格里共有几张笑脸。请你把所有的笑脸找出来。(在笑脸上画“○”,其他画“×”)
3.乐乐和芳芳一起玩游戏,规则如下:
(1)图中共有6个宝物;
(2)数字表示该方格周围(横、纵、斜)宝物的数量;
(3)数字所在的方格内没有宝物。
请仿照图1,在图2中画出宝物。(宝物用○表示)
图1 图2
21世纪教育网(www.21cnjy.com)
目 录
【课内精选一】确定物体的位置。 3
【课内精选二】数对与位置。 5
【课内精选三】描述并绘制路线图。 7
【奥数拓展一】在图形中确定物体的位置。 9
【奥数拓展二】数对与位置综合应用。 11
【奥数拓展三】描述并绘制路线图。 14
【奥数拓展四】数列与位置。 17
【奥数拓展五】方格游戏。 20
第二单元位置与方向(二)·思维素养篇【从课堂到奥数】
【课内精选一】确定物体的位置。
看图,填一填。以学校为观测点。
(1)小青家在学校( )方向( )米处。
(2)小华家在学校( )偏( )( )°的方向上。
(3)商店在学校( )方向( )米处。
(4)小红家在学校( )偏( )( )°的方向上。
(5)汽车站在学校( )方向( )米处。
【答案】(1) 正东 1000
(2) 东 北 34
(3) 正北 800
(4) 西 北 34
(5) 正西 600
【分析】确定物体位置的三大要素是:方向、角度、距离,同时根据图上的方向:上北下南、左西右东,以及角度和距离就可以确定方位;
同时通过对图的观察,图上一格代表实际距离200米,用图上的的格子数量乘200即可得到去每个地方的实际距离。
【详解】(1)小青家距离学校有5格,即:5×200=1000(米)
小青家在学校正东方向1000米处。
(2)小华家在学校东偏北34°的方向上。
90°-34°=56°
还可以说小华家在学校北偏东56米。(共两种答案)
(3)商店距离4格学校,即:4×200=800(米)
商店在学校正北方向800米处。
(4)小红家在学校西偏北34°的方向上。
或者:90°-34°=56°,
还可以说小红家在学校北偏西56°的方向上。(共两种答案)
(5)汽车距离学校有3个格子,即:3×200=600(米)
汽车站在学校正西方向600米处。
【点睛】本题主要考查方向的辨别,明确判定物体位置的三要素是解答本题的关键。
【专项训练】
量一量,填一填。
(1)野生动物馆在售票亭的( )偏( )( )°的方向上,距离是( )米。
(2)鸟岛在售票亭的( )偏( )( )°的方向上,距离是( )米。
(3)表演区在售票亭的( )偏( )( )°的方向上,距离是( )米。
(4)海洋馆在售票亭的( )偏( )( )°的方向上,距离是( )米。
【答案】(1) 东 北 40 100
(2) 北 西 45 200
(3) 西 南 25° 100
(4) 东 南 35 200
【分析】观察图形可知,图上1格表示50米,则野生动物馆到售票亭的距离为2×50=100米;鸟岛到售票亭的距离为4×50=200米;表演区到售票亭的距离为2×50=100米;海洋馆到售票亭的距离为4×50=200米;再根据“上北下南,左西右东”及测量出的角度填空即可。
【详解】(1)2×50=100(米)
野生动物馆在售票亭的东偏北40°(北偏东60°)的方向上,距离是100米。
(2)4×50=200(米)
鸟岛在售票亭的北偏西45°(西偏北45°)的方向上,距离是200米。
(3)2×50=100(米)
表演区在售票亭的西偏南25°(南偏西75°)的方向上,距离是100米。
(4)4×50=200(米)
海洋馆在售票亭的东偏南35°(南偏东55°)的方向上,距离是200米。
【点睛】本题考查方向和位置,明确“上北下南,左西右东”及测量出的角度是解题的关键。
【课内精选二】数对与位置。
看一看,填一填。
(1)用数对表示体育中心的位置是( )。
(2)以植物园为观测点,学校在植物园的( )面;以图书馆为观测点,剧院在( )方向上。
【答案】(1)(1,4)
(2) 南 南偏东
【分析】(1)根据利用数对表示物体位置的方法,用数对表示物体的位置时,列数在前,行数在后;
(2)根据地图上方向的规定“上北下南,左西右东”,先以学校为观测点,确定出植物园的位置;再以图书馆为观测点,确定出剧院的位置。
【详解】(1)用数对表示体育中心的位置是(1,4)。
(2)90°-37°=53°
以植物园为观测点,学校在植物园的南面;以图书馆为观测点,剧院在南偏东37°(东偏南53°)方向上。
【专项训练】
(1)小亮的位置用数对表示为( ),数对(y,4)表示的位置可能是( ),也可能是( )。
(2)小强在小明( )偏( )( )方向上。小明在小亮( )偏( )( )方向上。
【答案】(1) (5,2) 小明 小红
(2) 北 东 60° 北 西 45°
【分析】(1)用数对表示位置时,通常把竖排叫列,横排叫行。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。据此解答。
(2)明确观测点后,根据地图“上北下南,左西右东”的规定,结合夹角进行描述。
【详解】(1)小亮的位置用数对表示为(5,2);数对(y,4)表示的位置是第y列第4行,可能是小明,也可能是小红。
(2)小强在小明北偏东60°方向上。小明在小亮北偏西45°方向上。
【课内精选三】描述并绘制路线图。
一辆客车从起点站向东偏北30°方向行驶6千米,再向正东方向行驶4千米到达终点站。
①根据上面的描述,把客车行驶的路线补充完整。
②根据路线图,说说客车沿原路返回时所行驶的方向和路程。
【答案】①见详解
②见详解
【分析】①以图上的“上北下南,左西右东”为准,图例表示图上1厘米相当于实际距离2千米。
在客车行驶到6千米处的正东方向上画4÷2=2厘米长的线段,即是终点站。
②根据位置的相对性,观测点不同,方向相反,夹角的度数相同;由此写出客车沿原路返回时所行驶的方向和路程。
【详解】①如图:
②一辆客车从终点站向正西方向行驶4千米,再向西偏南30°(或南偏西60°)方向行驶6千米到达起点站。
【专项训练】
操作。
(1)一辆汽车从起点出发,先向( )偏( )( )°方向行驶( )千米到达A站。
(2)到达A站后,再向正西方向行驶2千米到达B站,最后向西偏北40°方向行驶4千米到达终点站。请在图中标出B站与终点站的位置。
【答案】(1)西;南;30;3
(2)见详解
【分析】以图上的“上北下南,左西右东”为准,图例表示图上1厘米相当于实际距离1千米。
(1)从图中可知,起点站与A站相距3厘米,那么实际相距1×3=3千米,根据图上的方向、角度和距离,描述出汽车从起点出发到A站的路线。
(2)以A站为观测点,在A站的正西方向上画2÷1=2厘米长的线段,即是B站;
再以B站为观测点,在B站的西偏北40°方向上画4÷1=4厘米长的线段,即是终点站;
据此在图中标出B站与终点站的位置。
【详解】(1)一辆汽车从起点出发,先向西偏南30°(或南偏西60°)方向行驶3千米到达A站。
(2)如图:
【奥数拓展一】在图形中确定物体的位置。
图中三角形ABC是等腰三角形。已知∠2=40°,AC=BC。点B在点C的( )方向上,点A在点C的东偏北( )°方向上。
【答案】 正西 80
【分析】以点C为观测点,根据“上北下南,左西右东”描述方向,则点B在点C的正西方向,等腰三角形中两个底角相等,根据三角形的内角和求出∠3的度数,∠3与∠4的和等于一个平角的度数,∠4=180°-∠3,求出∠4的度数,即可求得。
【详解】三角形ABC中,∠1=∠2=40°,且三角形的内角和为180°。
180°-40°-40°
=140°-40°
=100°
180°-100°=80°
所以,点B在点C的正西方向上,点A在点C的东偏北80°方向上。
【点睛】掌握等腰三角形的特征,并根据三角形的内角和与一个平角的度数求出∠4的度数是解答题目的关键。
【专项训练】
已知下图中每个方格的边长是1厘米,三角形ABC是一个等边三角形,那么,点C在点A的( )偏( ) ( )°方向( )厘米处。
【答案】 北 东 30 4
【分析】观察题意可知,AB长4厘米,根据等边三角形的特征,可知AC长也是4厘米,∠BAC是60°;根据平面图上方向的规定:上北下南,左西右东,以A点为观测点即可确定C点的方向;据此解答。
【详解】点C在点A的东偏北60°或北偏东30°方向4厘米处。
【点睛】此题主要考查依据方向(角度)和距离确定物体位置的方法,明确等边三角形的特征是解答本题的关键。
【奥数拓展二】数对与位置综合应用。
看图填空。
(1)如果A点的位置用数对(1,2)表示,那么B点的位置可用数对( )表示。
(2)如果一个小正方形的对角线长10米,点C在点B的南偏东45度方向20米处,请在图上标出C点;点D在A点的东偏南45度方向20米处,请在图上标出D点。
(3)连接ABCD四点,再画出将四边形ABCD向右平移3格后的图形。
【答案】(1)(3,6)
(2)(3)见详解
【分析】(1)用数对表示位置,数对的第一个数表示列,第二个数表示行,据此分析;
(2)弄清要标示的物体在哪个方位上,有多少度,按要求的方位和度数准确画图;注意各场所离中心点的距离,根据要求的比例画出相应的长度。
(3)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
【详解】(1)如果A点的位置用数对(1,2)表示,那么B点的位置可用数对(3,6)表示。
(2)
(3)
【点睛】用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。确定一个图形平移后的位置,除需要原来的位置外,还需要知道平移的方向、平移的距离。
【专项训练】
曾正同学是个数学迷。他在一张纸上画了10×10的方格用以研究有关图形的数学问题,假定一个方格的对角线长代表10m,所研究的点都是网格的交点。
(1)点(0,0)北偏东45°方向30m是点A,它的位置用数对表示是( )。
(2)点A北偏西45方向20m是点B,点B北偏东45°方向20m是点C,点C南偏东45°方向20m是点D。用A、B、C、D四个点顺次连接围成一个四边形,它的面积是多少?
(3)请你设计不同于点D的另一个点E使得以A、B、C、E为端点的线段围成四边形的面积与第(2)题用A、B、C、D四个点顺次连接所围成的四边形面积相等。点E可以有不同的设计,这样的点共有( )个,写出其中的四个点E:( )、( )、( )、( )。
【答案】图见详解;
(1)(3,3)
(2)1600m
(3)11;(5,2)、(5,3)、(5,6)、(5,8)
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数、平面图上方向的辨别“上北下南,左西右东”、方格的对角线长代表10m,即可描出点A,并用数对表示它的位置。
(2)同理,分别以点A的位置为观测点即可描出点B的位置、以点B的位置为观测点即可描出点C的位置、以点C的位置为观测点即可描出点D的位置,然后再把A、B、C、D连结成一个封闭图形。连结成的封闭图形是一个正方形,其边长是(20×2)米,根据正方形的面积计算公式“S=a2”即可求出它的面积。
(3)正方形ABCD看作是由三角形ABC与三角形ADC的面积之和,且三角形ABC与三角形ADC的面积相等。三角形ACD看作底为4格,高为2格三角形,当底不变,高是2格时,其面积也不会变,因此,第5列上的任一点为E,与AC组成的三角形面积都与三角形ADC的面积相等。这样四边形ABCE的面积就与正方形ABCD的面积相等。这样的点在本图上共有8个:(5,0)、(5,2)、(5,3)、5,4)、(5,6)、(5,7)、(5,8)、(5,10)。可以写出其中四个(答案不唯一)。
【详解】(1)点(0,0)北偏东45°方向30m是点A,它的位置用数对表示是(3,3)
(2)点A北偏西45方向20m是点B,点B北偏东45°方向20m是点C,点C南偏东45°方向20m是点D。用A、B、C、D四个点顺次连接围成一个四边形,它的面积是:
(20×2)
=40
=1600(m )
(3)设计不同于点D的另一个点E使得以A、B、C、E为端点的线段围成四边形的面积与第(2)题用A、B、C、D四个点顺次连接所围成的四边形面积相等。点E可以有不同的
设计,这样的点共有8个,写出其中的四个点E:(5,2)、(5,3)、(5,6)、(5,8)(答案不唯一)。
【点睛】此题考查的知识有:数对与位置、根据方向和距离确定物体的位置、正方形面积的计算、三角形面积的计算等。
【奥数拓展三】描述并绘制路线图。
如图是芳芳每天从家到学校的路线图。
(1)根据路线图把表格中的数据补充完整。
路线 方向 路程 时间
家→超市 5分钟
超市→医院 10分钟
医院→学校 9分钟
(2)芳芳每天从家出发到学校走多少米?平均每分钟走多少米?
【答案】(1)见详解。
(2)960米;40米
【分析】(1)先以家参照点建立方向标,向东偏北60°(或北偏东30°)方向走200米到超市;再以超市为参照点建立方向标,向东走400米到医院;最后以医院为参照点建立方向标,向东偏南30°(或南偏东60°)方向走360米到学校。
(2)把家到超市、超市到医院、医院到学校这三段路程加起来,即200+400+360,可求出芳芳每天从家出发到学校走的米数;再用5+10+9求出芳芳从家出发到学校走的分钟数(24分钟);最后根据路程÷时间=速度,用芳芳每天从家出发到学校走的米数÷从家出发到学校走的分钟数,可求出平均每分钟走的米数。
【详解】(1)如下图:
路线 方向 路程 时间
家→超市 东偏北60°(或北偏东30°) 200米 5分钟
超市→医院 东 400米 10分钟
医院→学校 东偏南30°(或南偏东60°) 360米 9分钟
(2)200+400+360=960(米)
960÷(5+10+9)
=960÷24
=40(米)
答:芳芳每天从家出发到学校走960米,平均每分钟走40米。
【专项训练】
小华从家出发,先向东走200米到达A地,再向东偏北45°方向行500米到达B地,最后向西偏北30°方向行300米到达终点C地。
(1)根据上面的描述,把小华走的路线图画完整。
(2)如果从终点C原路返回家里用了12分30秒,那么他返回时每分钟行多少米?
【答案】(1)见详解
(2)80米
【分析】(1)以图上的“上北下南,左西右东”为准,图例表示图上1厘米相当于实际距离100米。
小华从家出发,在家的正东方向画(200÷100)厘米长的线段,即是A地;
在A地的东偏北45°方向上画(500÷100)厘米长的线段,即是B地;
在B地的西偏北30°方向上画(300÷100)厘米长的线段,即是C地。
(2)已知从终点C原路返回家里用了12分30秒,根据“1分=60秒”可知,用时12.5分;
用加法求出从C地返回家的总路程,再根据“速度=路程÷时间”,即可求出他返回时的速度。
【详解】(1)200÷100=2(厘米)
500÷100=5(厘米)
300÷100=3(厘米)
如图:
(2)12分30秒=12.5分
(300+500+200)÷12.5
=1000÷12.5
=80(米)
答:他返回时每分钟行80米。
【奥数拓展四】数列与位置。
已知数列,,…,则第10个数是( )。
【答案】
【分析】通过观察可知,=,=,=…,以此类推,第n个数是,据此解答。
【详解】根据分析可知,第10个数是
=
=
=
【专项训练】
1.找规律、1、、、、…,这串数中第7个数是( )。
【答案】
【分析】根据、、可得相邻两个分数的分子之差为3,分母之差为4,又因为和的分子之差为6,分母之差为8,即两数之间应该是,=1。所以这串数中第7个数应该是的分子加上3,分母加上4之后所得的数。
【详解】16+3=19
19+4=23
所以这串数中第7个数是。
2.一列分数: 、、、、、、…,按规律,是这列分数中的第( )个。
【答案】28
【分析】观察数列可知,分母是2的分数有1个,分母是3的分数有2个,分母是4的分数有3个,发现分母是n的分数有(n-1)个,分子从1到n-1依次排列,据此解答即可。
【详解】由分析可知:
分母是2的分数有1个,分母是3的分数有2个,分母是4的分数有3个,分母是5的分数有4个,分母是6的分数有5个,分母是7的分数有6个,分母是8的分数有7个;
1+2+3+4+5+6+7
=(1+2+7)+(4+6)+(3+5)
=10+10+8
=20+8
=28
则按规律,是这列分数中的第28个。
【点睛】本题考查数列的排列规律,发现规律,利用规律是解题的关键。
3.瑞士数学教师巴尔末成功地从光谱数据,……中得到巴尔末公式,从而打开了光谱奥妙的大门。按这种规律写出的第5个数是( ),第8个数是( )。
【答案】
【分析】根据题意可知,分子的规律依次是32、42、52、62 分母的规律是:1×5、2×6、3×7、4×8 ;通过上述分子和分母的规律,可知,第几个数,分子就是这个数加2的平方,即(n+2)2,分母可以写成两个数相乘,后面的数比前面的数多4,则第几个数,它的分母就是n(n+4),由此即可解答。
【详解】当n=5时,
(n+2)2
=(5+2)2
=72
=49
n(n+4)
=5×(5+4)
=5×9
=45
即第5个数是;
当n=8时,
(n+2)2
=(8+2)2
=102
=100
n(n+4)
=8×(8+4)
=8×12
=96
即第8个数是。
【点睛】本题主要考查分数的变化规律,仔细的找到分子和分母的变化规律是解答的关键。
【奥数拓展五】方格游戏。
“扫雷”是一款经典的益智游戏,规则如下:
①图中阴影部分是雷区,共有10个雷;
②方格中的数字表示这个方格周围雷的个数。
例如:左图中标有“★”的方格周围有8个方格(标数的方格)。
请你根据上面的例图,完成下图。(是雷的标○,不是雷的标×)
【答案】见详解
【分析】根据题目规则,数字5周围的阴影部分都是雷,据此第四行的数字2周围已经有2个雷,所以这个数字2周围其他阴影部分都不是雷;第四行的数字3也已经有3个雷,所以这个数字3周围其他阴影部分都不是雷;第四行的数字3右边的数字1已经有1个雷,所以这个数字1周围其他阴影部分都不是雷;数字4已经有1个阴影部分不是雷,有3个是雷,说明还有1个是雷;第二行的数字3已经有3个雷,则这个数字3周围其他阴影部分不是雷;第六行第一个数字1,周围已经有2个不是雷,说明剩余1个阴影部分是雷;第七行第一个数字2,周围有2个雷;第七行第二个数字2已经有2个雷,说明剩余1个阴影部分不是雷;第六行第三个数字1有1个雷;第六行第二个数字1已经有1个雷,说明这个数字1周围其他阴影部分都不是雷;第五行第二个数字2已经有1个雷,2个不是雷,说明剩余1个是雷;第四行第二个数字2已经有2个雷,说明这个数字2周围其他地方都不是雷;据此作图。
【详解】如图所示:
【点睛】本题从数字一个个分析,能确定的地方先做好标记,是雷的标○,不是雷的标×,然后不能确定的地方根据做的标记进行分析即可。
【专项训练】
1.如图,每个小方块周围最多有8个小方块,外围没标数字的小方块是未探明的雷区,其中每个小方块最多有一个雷。内部的小方块没有雷,数字表示所在小方块周围的雷数。图中共有( )个雷。
【答案】16
【解析】如图,用小红旗表示不是雷,依次进行分析,可以得到所有不是雷的方格,剩下的方格中都是雷,总共16个。
【详解】如图所示:
图中共有16个雷。
【点睛】本题考查的是扫雷问题,扫雷实质上还是逻辑推理问题,在推理过程中,可以先把能够确定的地方标出来,然后再确定其它位置。
2.下面是找笑脸游戏,规则是:点开的方格中的数是几,就表示围着它的方格里共有几张笑脸。请你把所有的笑脸找出来。(在笑脸上画“○”,其他画“×”)
【答案】
【分析】首先从方格中没有数字的开始判断,判断出哪些方格中没有笑脸;然后根据点开的方格中是几,就代表周围的八个方格里有几个笑脸,判断出哪些方格中有笑脸即可。
【详解】右边的第二列、以及第三列和第四列的数字都是1,则可以判断最右边的一列的三个不是笑脸,右边第三列的中间一定是笑脸,则第四列中间的一个不是笑脸,左边第三列的两个也不是笑脸,由左边第三列的2判断出左边第二列的下面两个都是笑脸,由左下角的3可以判断出左第一列的中间是笑脸,有左上角的2可以判断第二列的上面的空不是笑脸。
答案如下图:
【点睛】此题主要考查了逻辑推理问题,考查了分析推理能力的应用,解答此题的关键是从方格中没有数字的开始判断,判断出哪些方格中没有笑脸。
3.乐乐和芳芳一起玩游戏,规则如下:
(1)图中共有6个宝物;
(2)数字表示该方格周围(横、纵、斜)宝物的数量;
(3)数字所在的方格内没有宝物。
请仿照图1,在图2中画出宝物。(宝物用○表示)
图1 图2
【答案】见详解
【分析】根据题意,只有6个宝物,尽量找一些重合的地方标记宝物。
①数字5代表5的周围有5个宝物,3的周围有3个宝物,如下图,则有两个“√”号的可以标记有宝物。
②分析5和另外一个3,如图,有两个“√”号的可以标记有宝物。
往下类推,找出所有的宝物。
【详解】
21世纪教育网(www.21cnjy.com)
【课内精选一】确定物体的位置。 3
【课内精选二】数对与位置。 4
【课内精选三】描述并绘制路线图。 5
【奥数拓展一】在图形中确定物体的位置。 6
【奥数拓展二】数对与位置综合应用。 7
【奥数拓展三】描述并绘制路线图。 8
【奥数拓展四】数列与位置。 9
【奥数拓展五】方格游戏。 10
第二单元位置与方向(二)思维素养篇【从课堂到奥数】
【课内精选一】确定物体的位置。
看图,填一填。以学校为观测点。
(1)小青家在学校( )方向( )米处。
(2)小华家在学校( )偏( )( )°的方向上。
(3)商店在学校( )方向( )米处。
(4)小红家在学校( )偏( )( )°的方向上。
(5)汽车站在学校( )方向( )米处。
【专项训练】
量一量,填一填。
(1)野生动物馆在售票亭的( )偏( )( )°的方向上,距离是( )米。
(2)鸟岛在售票亭的( )偏( )( )°的方向上,距离是( )米。
(3)表演区在售票亭的( )偏( )( )°的方向上,距离是( )米。
(4)海洋馆在售票亭的( )偏( )( )°的方向上,距离是( )米。
【课内精选二】数对与位置。
看一看,填一填。
(1)用数对表示体育中心的位置是( )。
(2)以植物园为观测点,学校在植物园的( )面;以图书馆为观测点,剧院在( )方向上。
【专项训练】
(1)小亮的位置用数对表示为( ),数对(y,4)表示的位置可能是( ),也可能是( )。
(2)小强在小明( )偏( )( )方向上。小明在小亮( )偏( )( )方向上。
【课内精选三】描述并绘制路线图。
一辆客车从起点站向东偏北30°方向行驶6千米,再向正东方向行驶4千米到达终点站。
①根据上面的描述,把客车行驶的路线补充完整。
②根据路线图,说说客车沿原路返回时所行驶的方向和路程。
【专项训练】
操作。
(1)一辆汽车从起点出发,先向( )偏( )( )°方向行驶( )千米到达A站。
(2)到达A站后,再向正西方向行驶2千米到达B站,最后向西偏北40°方向行驶4千米到达终点站。请在图中标出B站与终点站的位置。
【奥数拓展一】在图形中确定物体的位置。
图中三角形ABC是等腰三角形。已知∠2=40°,AC=BC。点B在点C的( )方向上,点A在点C的东偏北( )°方向上。
【专项训练】
已知下图中每个方格的边长是1厘米,三角形ABC是一个等边三角形,那么,点C在点A的( )偏( ) ( )°方向( )厘米处。
【奥数拓展二】数对与位置综合应用。
看图填空。
(1)如果A点的位置用数对(1,2)表示,那么B点的位置可用数对( )表示。
(2)如果一个小正方形的对角线长10米,点C在点B的南偏东45度方向20米处,请在图上标出C点;点D在A点的东偏南45度方向20米处,请在图上标出D点。
(3)连接ABCD四点,再画出将四边形ABCD向右平移3格后的图形。
【专项训练】
曾正同学是个数学迷。他在一张纸上画了10×10的方格用以研究有关图形的数学问题,假定一个方格的对角线长代表10m,所研究的点都是网格的交点。
(1)点(0,0)北偏东45°方向30m是点A,它的位置用数对表示是( )。
(2)点A北偏西45方向20m是点B,点B北偏东45°方向20m是点C,点C南偏东45°方向20m是点D。用A、B、C、D四个点顺次连接围成一个四边形,它的面积是多少?
(3)请你设计不同于点D的另一个点E使得以A、B、C、E为端点的线段围成四边形的面积与第(2)题用A、B、C、D四个点顺次连接所围成的四边形面积相等。点E可以有不同的设计,这样的点共有( )个,写出其中的四个点E:( )、( )、( )、( )。
【奥数拓展三】描述并绘制路线图。
如图是芳芳每天从家到学校的路线图。
(1)根据路线图把表格中的数据补充完整。
路线 方向 路程 时间
家→超市 5分钟
超市→医院 10分钟
医院→学校 9分钟
(2)芳芳每天从家出发到学校走多少米?平均每分钟走多少米?
【专项训练】
小华从家出发,先向东走200米到达A地,再向东偏北45°方向行500米到达B地,最后向西偏北30°方向行300米到达终点C地。
(1)根据上面的描述,把小华走的路线图画完整。
(2)如果从终点C原路返回家里用了12分30秒,那么他返回时每分钟行多少米?
【奥数拓展四】数列与位置。
已知数列,,…,则第10个数是( )。
【专项训练】
1.找规律、1、、、、…,这串数中第7个数是( )。
2.一列分数: 、、、、、、…,按规律,是这列分数中的第( )个。
3.瑞士数学教师巴尔末成功地从光谱数据,……中得到巴尔末公式,从而打开了光谱奥妙的大门。按这种规律写出的第5个数是( ),第8个数是( )。
【奥数拓展五】方格游戏。
“扫雷”是一款经典的益智游戏,规则如下:
①图中阴影部分是雷区,共有10个雷;
②方格中的数字表示这个方格周围雷的个数。
例如:左图中标有“★”的方格周围有8个方格(标数的方格)。
请你根据上面的例图,完成下图。(是雷的标○,不是雷的标×)
【专项训练】
1.如图,每个小方块周围最多有8个小方块,外围没标数字的小方块是未探明的雷区,其中每个小方块最多有一个雷。内部的小方块没有雷,数字表示所在小方块周围的雷数。图中共有( )个雷。
2.下面是找笑脸游戏,规则是:点开的方格中的数是几,就表示围着它的方格里共有几张笑脸。请你把所有的笑脸找出来。(在笑脸上画“○”,其他画“×”)
3.乐乐和芳芳一起玩游戏,规则如下:
(1)图中共有6个宝物;
(2)数字表示该方格周围(横、纵、斜)宝物的数量;
(3)数字所在的方格内没有宝物。
请仿照图1,在图2中画出宝物。(宝物用○表示)
图1 图2
21世纪教育网(www.21cnjy.com)
目 录
【课内精选一】确定物体的位置。 3
【课内精选二】数对与位置。 5
【课内精选三】描述并绘制路线图。 7
【奥数拓展一】在图形中确定物体的位置。 9
【奥数拓展二】数对与位置综合应用。 11
【奥数拓展三】描述并绘制路线图。 14
【奥数拓展四】数列与位置。 17
【奥数拓展五】方格游戏。 20
第二单元位置与方向(二)·思维素养篇【从课堂到奥数】
【课内精选一】确定物体的位置。
看图,填一填。以学校为观测点。
(1)小青家在学校( )方向( )米处。
(2)小华家在学校( )偏( )( )°的方向上。
(3)商店在学校( )方向( )米处。
(4)小红家在学校( )偏( )( )°的方向上。
(5)汽车站在学校( )方向( )米处。
【答案】(1) 正东 1000
(2) 东 北 34
(3) 正北 800
(4) 西 北 34
(5) 正西 600
【分析】确定物体位置的三大要素是:方向、角度、距离,同时根据图上的方向:上北下南、左西右东,以及角度和距离就可以确定方位;
同时通过对图的观察,图上一格代表实际距离200米,用图上的的格子数量乘200即可得到去每个地方的实际距离。
【详解】(1)小青家距离学校有5格,即:5×200=1000(米)
小青家在学校正东方向1000米处。
(2)小华家在学校东偏北34°的方向上。
90°-34°=56°
还可以说小华家在学校北偏东56米。(共两种答案)
(3)商店距离4格学校,即:4×200=800(米)
商店在学校正北方向800米处。
(4)小红家在学校西偏北34°的方向上。
或者:90°-34°=56°,
还可以说小红家在学校北偏西56°的方向上。(共两种答案)
(5)汽车距离学校有3个格子,即:3×200=600(米)
汽车站在学校正西方向600米处。
【点睛】本题主要考查方向的辨别,明确判定物体位置的三要素是解答本题的关键。
【专项训练】
量一量,填一填。
(1)野生动物馆在售票亭的( )偏( )( )°的方向上,距离是( )米。
(2)鸟岛在售票亭的( )偏( )( )°的方向上,距离是( )米。
(3)表演区在售票亭的( )偏( )( )°的方向上,距离是( )米。
(4)海洋馆在售票亭的( )偏( )( )°的方向上,距离是( )米。
【答案】(1) 东 北 40 100
(2) 北 西 45 200
(3) 西 南 25° 100
(4) 东 南 35 200
【分析】观察图形可知,图上1格表示50米,则野生动物馆到售票亭的距离为2×50=100米;鸟岛到售票亭的距离为4×50=200米;表演区到售票亭的距离为2×50=100米;海洋馆到售票亭的距离为4×50=200米;再根据“上北下南,左西右东”及测量出的角度填空即可。
【详解】(1)2×50=100(米)
野生动物馆在售票亭的东偏北40°(北偏东60°)的方向上,距离是100米。
(2)4×50=200(米)
鸟岛在售票亭的北偏西45°(西偏北45°)的方向上,距离是200米。
(3)2×50=100(米)
表演区在售票亭的西偏南25°(南偏西75°)的方向上,距离是100米。
(4)4×50=200(米)
海洋馆在售票亭的东偏南35°(南偏东55°)的方向上,距离是200米。
【点睛】本题考查方向和位置,明确“上北下南,左西右东”及测量出的角度是解题的关键。
【课内精选二】数对与位置。
看一看,填一填。
(1)用数对表示体育中心的位置是( )。
(2)以植物园为观测点,学校在植物园的( )面;以图书馆为观测点,剧院在( )方向上。
【答案】(1)(1,4)
(2) 南 南偏东
【分析】(1)根据利用数对表示物体位置的方法,用数对表示物体的位置时,列数在前,行数在后;
(2)根据地图上方向的规定“上北下南,左西右东”,先以学校为观测点,确定出植物园的位置;再以图书馆为观测点,确定出剧院的位置。
【详解】(1)用数对表示体育中心的位置是(1,4)。
(2)90°-37°=53°
以植物园为观测点,学校在植物园的南面;以图书馆为观测点,剧院在南偏东37°(东偏南53°)方向上。
【专项训练】
(1)小亮的位置用数对表示为( ),数对(y,4)表示的位置可能是( ),也可能是( )。
(2)小强在小明( )偏( )( )方向上。小明在小亮( )偏( )( )方向上。
【答案】(1) (5,2) 小明 小红
(2) 北 东 60° 北 西 45°
【分析】(1)用数对表示位置时,通常把竖排叫列,横排叫行。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。据此解答。
(2)明确观测点后,根据地图“上北下南,左西右东”的规定,结合夹角进行描述。
【详解】(1)小亮的位置用数对表示为(5,2);数对(y,4)表示的位置是第y列第4行,可能是小明,也可能是小红。
(2)小强在小明北偏东60°方向上。小明在小亮北偏西45°方向上。
【课内精选三】描述并绘制路线图。
一辆客车从起点站向东偏北30°方向行驶6千米,再向正东方向行驶4千米到达终点站。
①根据上面的描述,把客车行驶的路线补充完整。
②根据路线图,说说客车沿原路返回时所行驶的方向和路程。
【答案】①见详解
②见详解
【分析】①以图上的“上北下南,左西右东”为准,图例表示图上1厘米相当于实际距离2千米。
在客车行驶到6千米处的正东方向上画4÷2=2厘米长的线段,即是终点站。
②根据位置的相对性,观测点不同,方向相反,夹角的度数相同;由此写出客车沿原路返回时所行驶的方向和路程。
【详解】①如图:
②一辆客车从终点站向正西方向行驶4千米,再向西偏南30°(或南偏西60°)方向行驶6千米到达起点站。
【专项训练】
操作。
(1)一辆汽车从起点出发,先向( )偏( )( )°方向行驶( )千米到达A站。
(2)到达A站后,再向正西方向行驶2千米到达B站,最后向西偏北40°方向行驶4千米到达终点站。请在图中标出B站与终点站的位置。
【答案】(1)西;南;30;3
(2)见详解
【分析】以图上的“上北下南,左西右东”为准,图例表示图上1厘米相当于实际距离1千米。
(1)从图中可知,起点站与A站相距3厘米,那么实际相距1×3=3千米,根据图上的方向、角度和距离,描述出汽车从起点出发到A站的路线。
(2)以A站为观测点,在A站的正西方向上画2÷1=2厘米长的线段,即是B站;
再以B站为观测点,在B站的西偏北40°方向上画4÷1=4厘米长的线段,即是终点站;
据此在图中标出B站与终点站的位置。
【详解】(1)一辆汽车从起点出发,先向西偏南30°(或南偏西60°)方向行驶3千米到达A站。
(2)如图:
【奥数拓展一】在图形中确定物体的位置。
图中三角形ABC是等腰三角形。已知∠2=40°,AC=BC。点B在点C的( )方向上,点A在点C的东偏北( )°方向上。
【答案】 正西 80
【分析】以点C为观测点,根据“上北下南,左西右东”描述方向,则点B在点C的正西方向,等腰三角形中两个底角相等,根据三角形的内角和求出∠3的度数,∠3与∠4的和等于一个平角的度数,∠4=180°-∠3,求出∠4的度数,即可求得。
【详解】三角形ABC中,∠1=∠2=40°,且三角形的内角和为180°。
180°-40°-40°
=140°-40°
=100°
180°-100°=80°
所以,点B在点C的正西方向上,点A在点C的东偏北80°方向上。
【点睛】掌握等腰三角形的特征,并根据三角形的内角和与一个平角的度数求出∠4的度数是解答题目的关键。
【专项训练】
已知下图中每个方格的边长是1厘米,三角形ABC是一个等边三角形,那么,点C在点A的( )偏( ) ( )°方向( )厘米处。
【答案】 北 东 30 4
【分析】观察题意可知,AB长4厘米,根据等边三角形的特征,可知AC长也是4厘米,∠BAC是60°;根据平面图上方向的规定:上北下南,左西右东,以A点为观测点即可确定C点的方向;据此解答。
【详解】点C在点A的东偏北60°或北偏东30°方向4厘米处。
【点睛】此题主要考查依据方向(角度)和距离确定物体位置的方法,明确等边三角形的特征是解答本题的关键。
【奥数拓展二】数对与位置综合应用。
看图填空。
(1)如果A点的位置用数对(1,2)表示,那么B点的位置可用数对( )表示。
(2)如果一个小正方形的对角线长10米,点C在点B的南偏东45度方向20米处,请在图上标出C点;点D在A点的东偏南45度方向20米处,请在图上标出D点。
(3)连接ABCD四点,再画出将四边形ABCD向右平移3格后的图形。
【答案】(1)(3,6)
(2)(3)见详解
【分析】(1)用数对表示位置,数对的第一个数表示列,第二个数表示行,据此分析;
(2)弄清要标示的物体在哪个方位上,有多少度,按要求的方位和度数准确画图;注意各场所离中心点的距离,根据要求的比例画出相应的长度。
(3)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
【详解】(1)如果A点的位置用数对(1,2)表示,那么B点的位置可用数对(3,6)表示。
(2)
(3)
【点睛】用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。确定一个图形平移后的位置,除需要原来的位置外,还需要知道平移的方向、平移的距离。
【专项训练】
曾正同学是个数学迷。他在一张纸上画了10×10的方格用以研究有关图形的数学问题,假定一个方格的对角线长代表10m,所研究的点都是网格的交点。
(1)点(0,0)北偏东45°方向30m是点A,它的位置用数对表示是( )。
(2)点A北偏西45方向20m是点B,点B北偏东45°方向20m是点C,点C南偏东45°方向20m是点D。用A、B、C、D四个点顺次连接围成一个四边形,它的面积是多少?
(3)请你设计不同于点D的另一个点E使得以A、B、C、E为端点的线段围成四边形的面积与第(2)题用A、B、C、D四个点顺次连接所围成的四边形面积相等。点E可以有不同的设计,这样的点共有( )个,写出其中的四个点E:( )、( )、( )、( )。
【答案】图见详解;
(1)(3,3)
(2)1600m
(3)11;(5,2)、(5,3)、(5,6)、(5,8)
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数、平面图上方向的辨别“上北下南,左西右东”、方格的对角线长代表10m,即可描出点A,并用数对表示它的位置。
(2)同理,分别以点A的位置为观测点即可描出点B的位置、以点B的位置为观测点即可描出点C的位置、以点C的位置为观测点即可描出点D的位置,然后再把A、B、C、D连结成一个封闭图形。连结成的封闭图形是一个正方形,其边长是(20×2)米,根据正方形的面积计算公式“S=a2”即可求出它的面积。
(3)正方形ABCD看作是由三角形ABC与三角形ADC的面积之和,且三角形ABC与三角形ADC的面积相等。三角形ACD看作底为4格,高为2格三角形,当底不变,高是2格时,其面积也不会变,因此,第5列上的任一点为E,与AC组成的三角形面积都与三角形ADC的面积相等。这样四边形ABCE的面积就与正方形ABCD的面积相等。这样的点在本图上共有8个:(5,0)、(5,2)、(5,3)、5,4)、(5,6)、(5,7)、(5,8)、(5,10)。可以写出其中四个(答案不唯一)。
【详解】(1)点(0,0)北偏东45°方向30m是点A,它的位置用数对表示是(3,3)
(2)点A北偏西45方向20m是点B,点B北偏东45°方向20m是点C,点C南偏东45°方向20m是点D。用A、B、C、D四个点顺次连接围成一个四边形,它的面积是:
(20×2)
=40
=1600(m )
(3)设计不同于点D的另一个点E使得以A、B、C、E为端点的线段围成四边形的面积与第(2)题用A、B、C、D四个点顺次连接所围成的四边形面积相等。点E可以有不同的
设计,这样的点共有8个,写出其中的四个点E:(5,2)、(5,3)、(5,6)、(5,8)(答案不唯一)。
【点睛】此题考查的知识有:数对与位置、根据方向和距离确定物体的位置、正方形面积的计算、三角形面积的计算等。
【奥数拓展三】描述并绘制路线图。
如图是芳芳每天从家到学校的路线图。
(1)根据路线图把表格中的数据补充完整。
路线 方向 路程 时间
家→超市 5分钟
超市→医院 10分钟
医院→学校 9分钟
(2)芳芳每天从家出发到学校走多少米?平均每分钟走多少米?
【答案】(1)见详解。
(2)960米;40米
【分析】(1)先以家参照点建立方向标,向东偏北60°(或北偏东30°)方向走200米到超市;再以超市为参照点建立方向标,向东走400米到医院;最后以医院为参照点建立方向标,向东偏南30°(或南偏东60°)方向走360米到学校。
(2)把家到超市、超市到医院、医院到学校这三段路程加起来,即200+400+360,可求出芳芳每天从家出发到学校走的米数;再用5+10+9求出芳芳从家出发到学校走的分钟数(24分钟);最后根据路程÷时间=速度,用芳芳每天从家出发到学校走的米数÷从家出发到学校走的分钟数,可求出平均每分钟走的米数。
【详解】(1)如下图:
路线 方向 路程 时间
家→超市 东偏北60°(或北偏东30°) 200米 5分钟
超市→医院 东 400米 10分钟
医院→学校 东偏南30°(或南偏东60°) 360米 9分钟
(2)200+400+360=960(米)
960÷(5+10+9)
=960÷24
=40(米)
答:芳芳每天从家出发到学校走960米,平均每分钟走40米。
【专项训练】
小华从家出发,先向东走200米到达A地,再向东偏北45°方向行500米到达B地,最后向西偏北30°方向行300米到达终点C地。
(1)根据上面的描述,把小华走的路线图画完整。
(2)如果从终点C原路返回家里用了12分30秒,那么他返回时每分钟行多少米?
【答案】(1)见详解
(2)80米
【分析】(1)以图上的“上北下南,左西右东”为准,图例表示图上1厘米相当于实际距离100米。
小华从家出发,在家的正东方向画(200÷100)厘米长的线段,即是A地;
在A地的东偏北45°方向上画(500÷100)厘米长的线段,即是B地;
在B地的西偏北30°方向上画(300÷100)厘米长的线段,即是C地。
(2)已知从终点C原路返回家里用了12分30秒,根据“1分=60秒”可知,用时12.5分;
用加法求出从C地返回家的总路程,再根据“速度=路程÷时间”,即可求出他返回时的速度。
【详解】(1)200÷100=2(厘米)
500÷100=5(厘米)
300÷100=3(厘米)
如图:
(2)12分30秒=12.5分
(300+500+200)÷12.5
=1000÷12.5
=80(米)
答:他返回时每分钟行80米。
【奥数拓展四】数列与位置。
已知数列,,…,则第10个数是( )。
【答案】
【分析】通过观察可知,=,=,=…,以此类推,第n个数是,据此解答。
【详解】根据分析可知,第10个数是
=
=
=
【专项训练】
1.找规律、1、、、、…,这串数中第7个数是( )。
【答案】
【分析】根据、、可得相邻两个分数的分子之差为3,分母之差为4,又因为和的分子之差为6,分母之差为8,即两数之间应该是,=1。所以这串数中第7个数应该是的分子加上3,分母加上4之后所得的数。
【详解】16+3=19
19+4=23
所以这串数中第7个数是。
2.一列分数: 、、、、、、…,按规律,是这列分数中的第( )个。
【答案】28
【分析】观察数列可知,分母是2的分数有1个,分母是3的分数有2个,分母是4的分数有3个,发现分母是n的分数有(n-1)个,分子从1到n-1依次排列,据此解答即可。
【详解】由分析可知:
分母是2的分数有1个,分母是3的分数有2个,分母是4的分数有3个,分母是5的分数有4个,分母是6的分数有5个,分母是7的分数有6个,分母是8的分数有7个;
1+2+3+4+5+6+7
=(1+2+7)+(4+6)+(3+5)
=10+10+8
=20+8
=28
则按规律,是这列分数中的第28个。
【点睛】本题考查数列的排列规律,发现规律,利用规律是解题的关键。
3.瑞士数学教师巴尔末成功地从光谱数据,……中得到巴尔末公式,从而打开了光谱奥妙的大门。按这种规律写出的第5个数是( ),第8个数是( )。
【答案】
【分析】根据题意可知,分子的规律依次是32、42、52、62 分母的规律是:1×5、2×6、3×7、4×8 ;通过上述分子和分母的规律,可知,第几个数,分子就是这个数加2的平方,即(n+2)2,分母可以写成两个数相乘,后面的数比前面的数多4,则第几个数,它的分母就是n(n+4),由此即可解答。
【详解】当n=5时,
(n+2)2
=(5+2)2
=72
=49
n(n+4)
=5×(5+4)
=5×9
=45
即第5个数是;
当n=8时,
(n+2)2
=(8+2)2
=102
=100
n(n+4)
=8×(8+4)
=8×12
=96
即第8个数是。
【点睛】本题主要考查分数的变化规律,仔细的找到分子和分母的变化规律是解答的关键。
【奥数拓展五】方格游戏。
“扫雷”是一款经典的益智游戏,规则如下:
①图中阴影部分是雷区,共有10个雷;
②方格中的数字表示这个方格周围雷的个数。
例如:左图中标有“★”的方格周围有8个方格(标数的方格)。
请你根据上面的例图,完成下图。(是雷的标○,不是雷的标×)
【答案】见详解
【分析】根据题目规则,数字5周围的阴影部分都是雷,据此第四行的数字2周围已经有2个雷,所以这个数字2周围其他阴影部分都不是雷;第四行的数字3也已经有3个雷,所以这个数字3周围其他阴影部分都不是雷;第四行的数字3右边的数字1已经有1个雷,所以这个数字1周围其他阴影部分都不是雷;数字4已经有1个阴影部分不是雷,有3个是雷,说明还有1个是雷;第二行的数字3已经有3个雷,则这个数字3周围其他阴影部分不是雷;第六行第一个数字1,周围已经有2个不是雷,说明剩余1个阴影部分是雷;第七行第一个数字2,周围有2个雷;第七行第二个数字2已经有2个雷,说明剩余1个阴影部分不是雷;第六行第三个数字1有1个雷;第六行第二个数字1已经有1个雷,说明这个数字1周围其他阴影部分都不是雷;第五行第二个数字2已经有1个雷,2个不是雷,说明剩余1个是雷;第四行第二个数字2已经有2个雷,说明这个数字2周围其他地方都不是雷;据此作图。
【详解】如图所示:
【点睛】本题从数字一个个分析,能确定的地方先做好标记,是雷的标○,不是雷的标×,然后不能确定的地方根据做的标记进行分析即可。
【专项训练】
1.如图,每个小方块周围最多有8个小方块,外围没标数字的小方块是未探明的雷区,其中每个小方块最多有一个雷。内部的小方块没有雷,数字表示所在小方块周围的雷数。图中共有( )个雷。
【答案】16
【解析】如图,用小红旗表示不是雷,依次进行分析,可以得到所有不是雷的方格,剩下的方格中都是雷,总共16个。
【详解】如图所示:
图中共有16个雷。
【点睛】本题考查的是扫雷问题,扫雷实质上还是逻辑推理问题,在推理过程中,可以先把能够确定的地方标出来,然后再确定其它位置。
2.下面是找笑脸游戏,规则是:点开的方格中的数是几,就表示围着它的方格里共有几张笑脸。请你把所有的笑脸找出来。(在笑脸上画“○”,其他画“×”)
【答案】
【分析】首先从方格中没有数字的开始判断,判断出哪些方格中没有笑脸;然后根据点开的方格中是几,就代表周围的八个方格里有几个笑脸,判断出哪些方格中有笑脸即可。
【详解】右边的第二列、以及第三列和第四列的数字都是1,则可以判断最右边的一列的三个不是笑脸,右边第三列的中间一定是笑脸,则第四列中间的一个不是笑脸,左边第三列的两个也不是笑脸,由左边第三列的2判断出左边第二列的下面两个都是笑脸,由左下角的3可以判断出左第一列的中间是笑脸,有左上角的2可以判断第二列的上面的空不是笑脸。
答案如下图:
【点睛】此题主要考查了逻辑推理问题,考查了分析推理能力的应用,解答此题的关键是从方格中没有数字的开始判断,判断出哪些方格中没有笑脸。
3.乐乐和芳芳一起玩游戏,规则如下:
(1)图中共有6个宝物;
(2)数字表示该方格周围(横、纵、斜)宝物的数量;
(3)数字所在的方格内没有宝物。
请仿照图1,在图2中画出宝物。(宝物用○表示)
图1 图2
【答案】见详解
【分析】根据题意,只有6个宝物,尽量找一些重合的地方标记宝物。
①数字5代表5的周围有5个宝物,3的周围有3个宝物,如下图,则有两个“√”号的可以标记有宝物。
②分析5和另外一个3,如图,有两个“√”号的可以标记有宝物。
往下类推,找出所有的宝物。
【详解】
21世纪教育网(www.21cnjy.com)
