人教版六年级下册数学2式与方程 比和比例课件(共32张PPT)
文档属性
| 名称 | 人教版六年级下册数学2式与方程 比和比例课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-16 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
人教版数学 六年级下册 第六单元 总复习
整体复习
用字母表示数
你会用字母表示什么?写在表中。
数量 数量关系 计算公式 运算定律 其他
一班男生有a人,女生有b人,一共有(a+b)人。 s=vt V=Sh a+b=b+a 计算法则:
一班男生有a人,女生有b人,男生比女生多(a-b)人。 c=at C=4a S=a (a+b)+c=a+(b+c) 重复出现的规律:
ABBABBABB……
每包有m颗糖,n包有mn颗糖。 c=ax C=2(a+b) S=ab ab=ba 计量单位:
cm、dm、m、km……
有x个苹果平均分给y个小朋友每人分得(x÷y)个。 (a+b)÷2 C=πd=2πr S=πr (ab)c=a(bc) (a+b)c=ac+bc 点、线段
用字母简明地表达数量,除此之外,我们还可以用字母表达数量关系、运算定律和计算公式等等。
想一想,在一个含有字母的式子里,数与字母、字母与字母相乘,书写时应注意什么?
1.含有字母的式子里,数和字母中间的乘号可以记作“·”也可以省略不写。
2.省略乘号时,应该把数写在字母的前面。
3.数与数之间的乘号不能省略。加号、减号、除号都不能省略。
用字母表示数
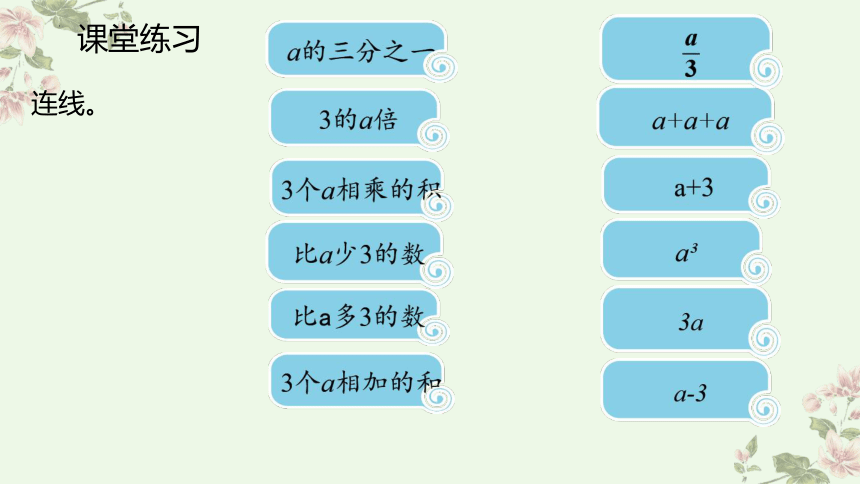
连线。
课堂练习
方 程
方程和等式有何联系与区别?
所有的方程一定是等式,但等式不一定是方程。
等式
方程
方 程
你能将韦恩图补充完整吗?
课堂活动
解方程
等式性质1:等式两边同时加上(减去)同一个数,结果仍然相等。
解:
解:
等式性质2:等式两边同时乘(除以)同一个不为0的数,结果仍然相等。
1.学校买来9个足球,每个a元,又买来b个篮球,每个58元。
9a表示____________________________;
58b表示___________________________;
58-a表示___________________________;
9a+58b表示__________________________;
如果a=45,b=6,则9a+58b=_________;
课堂练习
9个足球的总价
b个篮球的总价
篮球单价比足球单价贵的价钱
买9个足球和b个篮球共用的钱
753
独立完成,时间限定2分钟。
【例1】聪聪看一本500页的故事书,已经看了5天,每天看x页,已经看了( )页;当x=30时,还剩下( )页。
【变式1】每个足球x元,李老师买了4个足球,付了200元,找回( )元,如果x=45,应找回( )元。
5x
讲义练习
350
练习
【例2】解方程
6.三个连续的自然数,中间的数是a,则a的前边和后边分别是______和_____。
a-1
a+1
7.当n表示所有的自然数0,1,2,3,4,5……时,2n表示什么数?2n+1呢?
2n表示所有的正偶数,2n+1表示所有的正奇数。
4.用小棒摆正方形,如下图所示。
(1)你能发现什么规律?如果摆n个正方形,需要______根小棒。
(2)摆150个正方形,需要_____根小棒。
拓展练习
4+3×0
4+3×1
4+3×2
n
4+3×(n-1)
3n+1
451
3×150+1
人教版数学 六年级下册 第六单元 总复习
(第2课时)
方法总结
用方程解决实际问题有哪些步骤?
8.一台电视机打八五折后售价为2975元,这台电视机原价是多少钱?
85%
课堂练习
原价=现价÷折扣
方法一:
原价×折扣=现价
方法二:
课堂练习
12.商店卖一种书包,如果每个售价为150元,那么售价的60%是进价,售价的40%就是赚的钱。现在要搞促销活动,为保证一个书包赚的钱不少于30元,应该怎样确定折扣?
(折后)售价-进价=利润
【例3】A、B两地相距350千米,甲、乙两辆汽车同时从A、B两地出发,相向而行,经过2.5小时相遇。甲车每小时行65千米,乙车每小时行多少千米?(列方程解答)
讲义练习
解:设乙车每小时行x千米,可得方程:
(65+x)×2.5=350
(65+x)×2.5÷2.5=350÷2.5
65+x=140
65+x-65=140-65
x=140-65
x=75
答:乙车每小时行75千米。
同时相向而行:
相遇路程=速度和×相遇时间
相遇时间=相遇路程÷速度和
速度和=相遇路程÷相遇时间
【变式3】甲、乙两艘轮船同时沿一条海上航道从青岛开往广州,甲船每小时行29千米,乙船每小时行32千米。几小时后两船相距10.5千米?(列方程解答)
讲义练习
【例4】清明节,实验小学组织五、六年级共390名学生去参加“烈士陵园祭扫”活动。其中六年级参加的人数是五年级的1.6倍。五、六年级各参加了多少人?(列方程解答)
讲义练习
五年级参加的人数+六年级参加的人数=390
单位“1”
解:设五年级参加x人,则六年级参加1.6x人。
x+1.6x=390
人教版数学 六年级下册 第六单元 总复习
比和比例
整体复习
知识梳理
比的后项不能是零。
知识梳理
比 比例
意义 两个数的比表示两个数相除。 表示两个比相等的式子叫比例。
各部分 名称
基本性质 比的前项和后项同时乘或除以相同的数(0除外),比值不变。 在比例里,两个外项的积等于两个内项的积。
复习巩固
1.在下表中写出比例的一些知识,再举例说明。
课本P84.1
2.比与分数、除法有什么联系?填写下表。说一说它们的区别。
联系 各部分名称 分数 分子 分数线 分数值 分数值
除法 被除数 除号 除数 商
比 前项 比号 后项 比值
可以用字母表示为:
复习巩固
课本P84.2
复习巩固
3.举例说说比的基本性质、分数的基本性质和商不变规律之间有什么联系?
比的基本性质:
比的前项和后项同时乘或除相同的数(0除外),比值不变。
分数的基本性质:
分数的分子和分母同时乘或除相同的数(0除外),分数值不变。
商不变规律:
被除数和除数同时乘或除相同的数(0除外),商不变。
虽然说法不同,但是本质一样!
课本P84.3
复习巩固
4.你是怎样判断两种相关联的量是正比例关系还是反比例关系?
找变量
分析数量关系,确定两个量是相关联的量。
看定量
分析他们之间的关系是比值一定,还是积一定。
判 断
如果比值一定,两个相关联的量成正比例关系。
如果乘积一定,两个相关联的量成反比例关系。
课本P84.4
正比例:
两种相关联的量,其中一种量增加,另一种量也随着增加,一种量减少,另一种量也随着减少;两种量的比值一定。
反比例:
两种相关联的量,其中一种量增加,另一种量反而减少,一种量减少,另一种量反而增加;两种量的积一定。
单价一定,数量和总价。
正比例
路程一定,速度和时间。
反比例
感谢您的聆听与观看
人教版数学 六年级下册 第六单元 总复习
整体复习
用字母表示数
你会用字母表示什么?写在表中。
数量 数量关系 计算公式 运算定律 其他
一班男生有a人,女生有b人,一共有(a+b)人。 s=vt V=Sh a+b=b+a 计算法则:
一班男生有a人,女生有b人,男生比女生多(a-b)人。 c=at C=4a S=a (a+b)+c=a+(b+c) 重复出现的规律:
ABBABBABB……
每包有m颗糖,n包有mn颗糖。 c=ax C=2(a+b) S=ab ab=ba 计量单位:
cm、dm、m、km……
有x个苹果平均分给y个小朋友每人分得(x÷y)个。 (a+b)÷2 C=πd=2πr S=πr (ab)c=a(bc) (a+b)c=ac+bc 点、线段
用字母简明地表达数量,除此之外,我们还可以用字母表达数量关系、运算定律和计算公式等等。
想一想,在一个含有字母的式子里,数与字母、字母与字母相乘,书写时应注意什么?
1.含有字母的式子里,数和字母中间的乘号可以记作“·”也可以省略不写。
2.省略乘号时,应该把数写在字母的前面。
3.数与数之间的乘号不能省略。加号、减号、除号都不能省略。
用字母表示数
连线。
课堂练习
方 程
方程和等式有何联系与区别?
所有的方程一定是等式,但等式不一定是方程。
等式
方程
方 程
你能将韦恩图补充完整吗?
课堂活动
解方程
等式性质1:等式两边同时加上(减去)同一个数,结果仍然相等。
解:
解:
等式性质2:等式两边同时乘(除以)同一个不为0的数,结果仍然相等。
1.学校买来9个足球,每个a元,又买来b个篮球,每个58元。
9a表示____________________________;
58b表示___________________________;
58-a表示___________________________;
9a+58b表示__________________________;
如果a=45,b=6,则9a+58b=_________;
课堂练习
9个足球的总价
b个篮球的总价
篮球单价比足球单价贵的价钱
买9个足球和b个篮球共用的钱
753
独立完成,时间限定2分钟。
【例1】聪聪看一本500页的故事书,已经看了5天,每天看x页,已经看了( )页;当x=30时,还剩下( )页。
【变式1】每个足球x元,李老师买了4个足球,付了200元,找回( )元,如果x=45,应找回( )元。
5x
讲义练习
350
练习
【例2】解方程
6.三个连续的自然数,中间的数是a,则a的前边和后边分别是______和_____。
a-1
a+1
7.当n表示所有的自然数0,1,2,3,4,5……时,2n表示什么数?2n+1呢?
2n表示所有的正偶数,2n+1表示所有的正奇数。
4.用小棒摆正方形,如下图所示。
(1)你能发现什么规律?如果摆n个正方形,需要______根小棒。
(2)摆150个正方形,需要_____根小棒。
拓展练习
4+3×0
4+3×1
4+3×2
n
4+3×(n-1)
3n+1
451
3×150+1
人教版数学 六年级下册 第六单元 总复习
(第2课时)
方法总结
用方程解决实际问题有哪些步骤?
8.一台电视机打八五折后售价为2975元,这台电视机原价是多少钱?
85%
课堂练习
原价=现价÷折扣
方法一:
原价×折扣=现价
方法二:
课堂练习
12.商店卖一种书包,如果每个售价为150元,那么售价的60%是进价,售价的40%就是赚的钱。现在要搞促销活动,为保证一个书包赚的钱不少于30元,应该怎样确定折扣?
(折后)售价-进价=利润
【例3】A、B两地相距350千米,甲、乙两辆汽车同时从A、B两地出发,相向而行,经过2.5小时相遇。甲车每小时行65千米,乙车每小时行多少千米?(列方程解答)
讲义练习
解:设乙车每小时行x千米,可得方程:
(65+x)×2.5=350
(65+x)×2.5÷2.5=350÷2.5
65+x=140
65+x-65=140-65
x=140-65
x=75
答:乙车每小时行75千米。
同时相向而行:
相遇路程=速度和×相遇时间
相遇时间=相遇路程÷速度和
速度和=相遇路程÷相遇时间
【变式3】甲、乙两艘轮船同时沿一条海上航道从青岛开往广州,甲船每小时行29千米,乙船每小时行32千米。几小时后两船相距10.5千米?(列方程解答)
讲义练习
【例4】清明节,实验小学组织五、六年级共390名学生去参加“烈士陵园祭扫”活动。其中六年级参加的人数是五年级的1.6倍。五、六年级各参加了多少人?(列方程解答)
讲义练习
五年级参加的人数+六年级参加的人数=390
单位“1”
解:设五年级参加x人,则六年级参加1.6x人。
x+1.6x=390
人教版数学 六年级下册 第六单元 总复习
比和比例
整体复习
知识梳理
比的后项不能是零。
知识梳理
比 比例
意义 两个数的比表示两个数相除。 表示两个比相等的式子叫比例。
各部分 名称
基本性质 比的前项和后项同时乘或除以相同的数(0除外),比值不变。 在比例里,两个外项的积等于两个内项的积。
复习巩固
1.在下表中写出比例的一些知识,再举例说明。
课本P84.1
2.比与分数、除法有什么联系?填写下表。说一说它们的区别。
联系 各部分名称 分数 分子 分数线 分数值 分数值
除法 被除数 除号 除数 商
比 前项 比号 后项 比值
可以用字母表示为:
复习巩固
课本P84.2
复习巩固
3.举例说说比的基本性质、分数的基本性质和商不变规律之间有什么联系?
比的基本性质:
比的前项和后项同时乘或除相同的数(0除外),比值不变。
分数的基本性质:
分数的分子和分母同时乘或除相同的数(0除外),分数值不变。
商不变规律:
被除数和除数同时乘或除相同的数(0除外),商不变。
虽然说法不同,但是本质一样!
课本P84.3
复习巩固
4.你是怎样判断两种相关联的量是正比例关系还是反比例关系?
找变量
分析数量关系,确定两个量是相关联的量。
看定量
分析他们之间的关系是比值一定,还是积一定。
判 断
如果比值一定,两个相关联的量成正比例关系。
如果乘积一定,两个相关联的量成反比例关系。
课本P84.4
正比例:
两种相关联的量,其中一种量增加,另一种量也随着增加,一种量减少,另一种量也随着减少;两种量的比值一定。
反比例:
两种相关联的量,其中一种量增加,另一种量反而减少,一种量减少,另一种量反而增加;两种量的积一定。
单价一定,数量和总价。
正比例
路程一定,速度和时间。
反比例
感谢您的聆听与观看
