2024-2025学年人教A版必修二单元测试:第九章 统计
文档属性
| 名称 | 2024-2025学年人教A版必修二单元测试:第九章 统计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年人教A版必修二单元测试:第九章 统计
一、选择题
1.从小到大排列的数据1,2,3,5,6,7,8,9,10,14,15,18的下四分位数为( )
A.3 B.4 C.10 D.12
2.某校高一年级有男生300人,女生200人,按性别进行分层,用分层随机抽样的方法从该校高一年级学生中抽出一个容量为150的样本.如果样本按比例分配,那么男生、女生应分别抽取的人数为( )
A.75;75 B.90;60 C.60;90 D.100;50
3.“幸福感指数”是指人们主观地评价自己目前生活状态的满意程度的指标,常用区间内的一个数来表示,该数越接近10表示满意程度越高.现随机抽取10位某小区居民,他们的幸福感指数分别为3,4,5,5,6,6,7,8,9,10,则这组数据的第80百分位数是( )
A.7.5 B.8 C.8.5 D.9
4.下列说法不正确的是( )
A.一组数据10,11,11,12,13,14,16,18,20,22的第60百分位数为14
B.若随机变量X服从正态分布,且,则
C.若线性相关系数越接近1,则两个变量的线性相关程度越高
D.对具有线性相关关系的变量x、y,且回归方程为,若样本点的中心为,则实数m的值是
5.已知某学校高三年级甲、乙、丙三个班级人数分别为40,30,50,学校计划采用按比例分配的分层随机抽样的方法在三个班级中评选优秀学生,已知乙班分配到的优秀学生名单为6人,则高三年级三个班优秀学生总人数为( )
A.16 B.30 C.24 D.18
6.已知样本数据10,11,9,13,10,9,12,则这组样本数据的上四分位数为( )
A.9 B.10 C.11 D.12
7.甲、乙两个跑步爱好者利用微信运动记录了去年下半年每个月的跑步里程(单位:公里),现将两人的数据绘制成如图所示的折线图,则下列结论中错误的是( )
A.甲跑步里程的极差等于110
B.乙跑步里程的中位数是273
C.分别记甲、乙下半年每月跑步里程的平均数为,,则
D.分别记甲乙下半年每月跑步里程的标准差为,,则
8.有一组样本数据:15,16,11,11,14,20,11,13,13,24,13,18,则这组样本数据的上四分位数是( )
A.11 B.12 C.16 D.17
二、多项选择题
9.下列说法正确的是( )
A.已知随机变量X服从二项分布,则
B.设随机变量X服从正态分布,若,则
C.已知一组数据为1,2,3,4,5,6,7,8,9,10,则它的第70百分位数为7
D.若事件A,B满足,,,则事件A,B相互独立
10.已知某省2023年各地市地区生产总值的占比如图所示,则根据图中关于该省2023年各地市地区生产总值占比的统计情况,下列结论正确的是( )
A.A市2023年地区生产总值比B市2023年地区生产总值多
B.图中11个地市2023年地区生产总值占比的分位数为
C.图中11个地市2023年地区生产总值占比的分位数为
D.若该省2024年各地市地区生产总值的增长率相等,则该省2024年各地市地区生产总值的占比不变
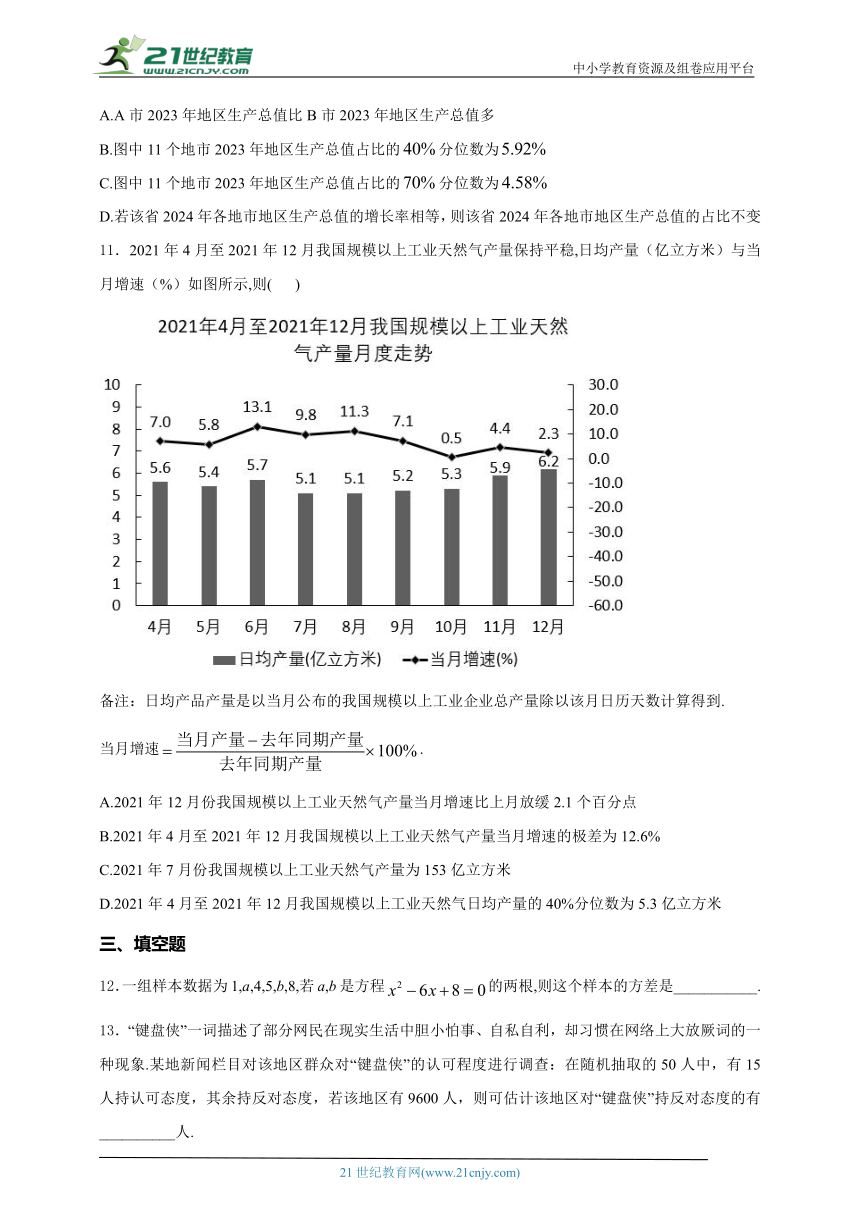
11.2021年4月至2021年12月我国规模以上工业天然气产量保持平稳,日均产量(亿立方米)与当月增速(%)如图所示,则( )
备注:日均产品产量是以当月公布的我国规模以上工业企业总产量除以该月日历天数计算得到.
当月增速.
A.2021年12月份我国规模以上工业天然气产量当月增速比上月放缓2.1个百分点
B.2021年4月至2021年12月我国规模以上工业天然气产量当月增速的极差为12.6%
C.2021年7月份我国规模以上工业天然气产量为153亿立方米
D.2021年4月至2021年12月我国规模以上工业天然气日均产量的40%分位数为5.3亿立方米
三、填空题
12.一组样本数据为1,a,4,5,b,8,若a,b是方程的两根,则这个样本的方差是___________.
13.“键盘侠”一词描述了部分网民在现实生活中胆小怕事、自私自利,却习惯在网络上大放厥词的一种现象.某地新闻栏目对该地区群众对“键盘侠”的认可程度进行调查:在随机抽取的50人中,有15人持认可态度,其余持反对态度,若该地区有9600人,则可估计该地区对“键盘侠”持反对态度的有__________人.
14.下列命题中:
①某校共有男生2700人,女生1800人,用比例分配的分层随机抽样抽取容量为90的样本进行健康测试,则样本中男生有54人;
②随着试验次数n的增大,一个随机事件A发生的频率会逐渐稳定于事件A发生的概率;
③数据4,8,10,14的方差是2,4,5,7的方差的2倍;
④从3个红球和2个白球中任取两个球,记事件“取出的两球均为红球”,事件“取出的两个球颜色不同”,则事件A与B互斥而不对立;
其中正确命题的编号为__________.
四、解答题
15.已知某科技公司的某型号芯片的各项指标经过全面检测后,分为I级和Ⅱ级,两种品级芯片的某项指标的频率分布直方图如图所示:
若只利用该指标制定一个标准,需要确定临界值K,将该指标大于K的产品应用于A型手机,小于或等于K的产品应用于B型手机.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.
(1)若临界值,请估计该公司生产的1000个该型号芯片I级品和1000个Ⅱ级品中应用于A型手机的芯片个数;
(2)设且,现有足够多的芯片I级品 Ⅱ级品,分别应用于A型手机 B型手机各1万部的生产:
方案一:直接将该芯片I级品应用于A型手机,其中该指标小于等于临界值K的芯片会导致芯片生产商每部手机损失800元;直接将该芯片Ⅱ级品应用于B型手机,其中该指标大于临界值K的芯片,会导致芯片生产商每部手机损失400元;
方案二:重新检测芯片I级品,II级品的该项指标,并按规定正确应用于手机型号,会避免方案一的损失费用,但检测费用共需要130万元;
请求出按方案一,芯片生产商损失费用的估计值(单位:万元)的表达式,并从芯片生产商的成本考虑,选择合理的方案.
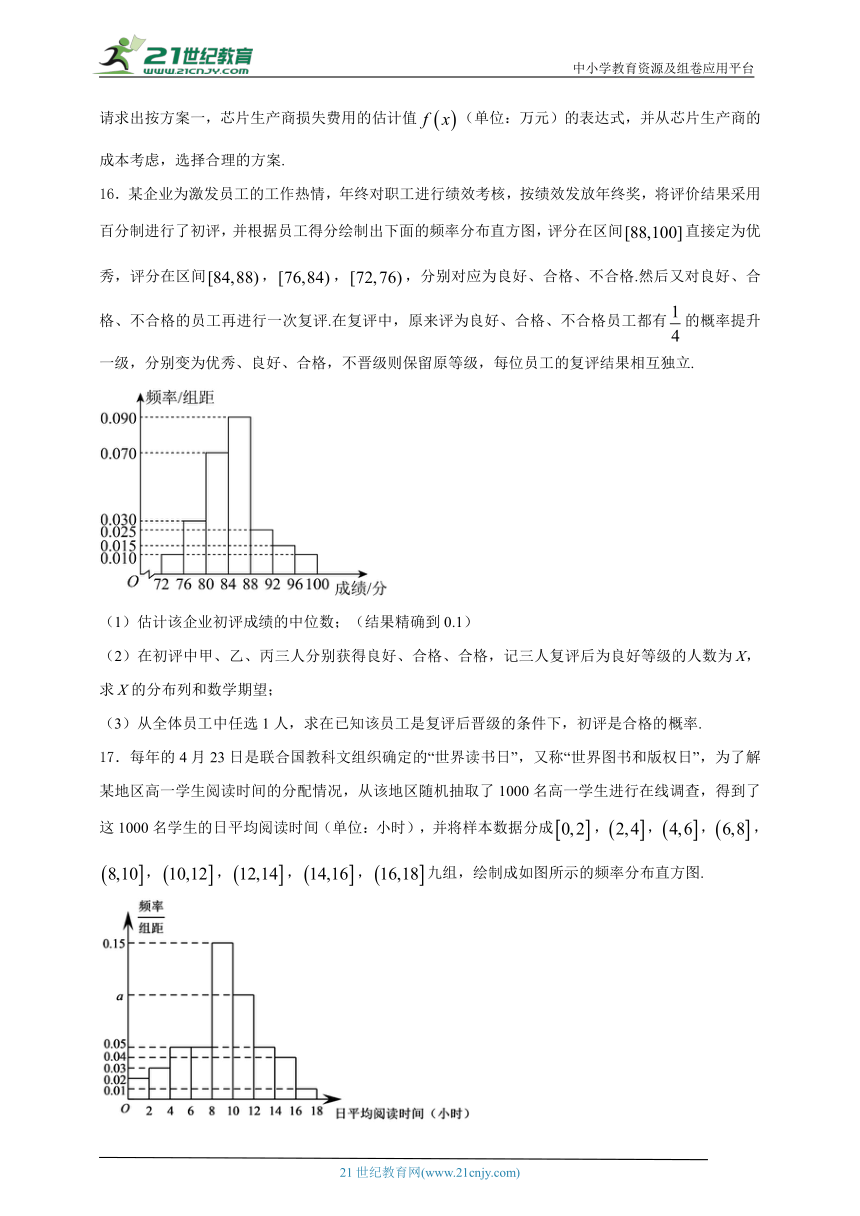
16.某企业为激发员工的工作热情,年终对职工进行绩效考核,按绩效发放年终奖,将评价结果采用百分制进行了初评,并根据员工得分绘制出下面的频率分布直方图,评分在区间直接定为优秀,评分在区间,,,分别对应为良好、合格、不合格.然后又对良好、合格、不合格的员工再进行一次复评.在复评中,原来评为良好、合格、不合格员工都有的概率提升一级,分别变为优秀、良好、合格,不晋级则保留原等级,每位员工的复评结果相互独立.
(1)估计该企业初评成绩的中位数;(结果精确到0.1)
(2)在初评中甲、乙、丙三人分别获得良好、合格、合格,记三人复评后为良好等级的人数为X,求X的分布列和数学期望;
(3)从全体员工中任选1人,求在已知该员工是复评后晋级的条件下,初评是合格的概率.
17.每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”,为了解某地区高一学生阅读时间的分配情况,从该地区随机抽取了1000名高一学生进行在线调查,得到了这1000名学生的日平均阅读时间(单位:小时),并将样本数据分成,,,,,,,,九组,绘制成如图所示的频率分布直方图.
(1)求a的值:
(2)为进一步了解这1000名学生数字媒体阅读时间和纸质图书阅读时间的分配情况,从日平均阅读时间在,两组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人,记日平均阅读时间在内的学生人数为X,求X的分布列和数学期望.
18.某公司采购了一批零件,为了检测这批零件是否合格,从中随机抽测120个零件的长度(单位:分米),将数据分成,,,,,这6组,得到如图的频率分布直方图,其中长度大于或等于1.59分米的零件有20个,其长度分别为1.59,1.59,1.61,1.61,1.62,1.63,1.63,1.64,1.65,1.65,1.65,1.65,1.66,1.67,1.68,1.69,1.69,1.71,1.72,1.74.以这120个零件在各组的长度的频率估计整批零件在各组长度的概率.
(1)求这批零件的长度大于1.60分米的频率,并求频率分布直方图中m,n,t的值.
(2)若从这批零件中随机选取3个,记X为抽取的零件长度在的个数,求X的分布列和数学期望.
(3)若变量S满足且,则称变量S满足近似于正态分布的概率分布.如果这批零件的长度Y满足近似于正态分布的概率分布,则认为这批零件是合格的将顺利被签收,否则,公司将拒绝签收.试问:该批零件能否被签收?
19.治疗某种疾病有一种传统药和一种创新药,治疗效果对比试验数据如下:服用创新药的50名患者中有40名治愈;服用传统药的400名患者中有120名未治愈.
(1)补全列联表(单位:人),并根据小概率值的独立性检验,分析创新药的疗效是否比传统药好;
药物 疗效 合计
治愈 未治愈
创新药
传统药
合计
(2)从服用传统药的400名患者中按疗效比例分层随机抽取10名,在这10人中随机抽取8人进行回访,用X表示回访中治愈者的人数,求X的分布列及均值.
附:,
参考答案
1.答案:B
解析:数据共12个,,
故从小到大,选择第3和第4个数的平均数作为下四分位数,即.
故选:B.
2.答案:B
解析:由题意可得,样本中应抽取的男生有名,
样本中应抽取的男生有名.
故选:B.
3.答案:C
解析:因为,
所以第80百分位数是.
故选:C
4.答案:A
解析:对A:因为,所以第60百分位数为,A错误;
对B:若随机变量X服从正态分布,且,
则,
则,B正确;
对C:若线性相关系数越接近1,则两个变量的线性相关性越强,C正确;
对于D,样本点的中心为,所以,,
因为满足线性回归方程,所以,所以,D正确.
故选:A.
5.答案:C
解析:甲、乙、丙三个班级人数比为,由分层随机抽样知,三个班级优秀学生名额分别为8,6,10,
所以高三年级三个班优秀学生总人数为人.
故选:C
6.答案:D
解析:将样本数据按从小到大的顺序排列为:9,9,10,10,11,12,13.
上四分位数即75%分位数,,
所以该组数据的上四分位数为从小到大排列的第6个数,即12,
故选:D.
7.答案:C
解析:
8.答案:D
解析:将样本数据由小到大排列依次为:11,11,11,13,13,13,14,15,16,18,20,24,
因为上四分位数是第分位数,则,所以这组数据的上四分位数为.
故选:D.
9.答案:AD
解析:因为随机变量X服从二项分布,则,故A正确;
因为随机变量X服从正态分布,则对称轴为,,故B错误;
这组数据的第70百分位数为,故C错误;
因为,所以,所以事件A,B相互独立.
故选:AD.
10.答案:ABD
解析:由图中统计数据,可得A市2023年地区生产总值比B市2023年地区生产总值多,A正确.
因为,所以图中11个地市2023年地区生产总值占比的分位数为,B正确.
因为,所以图中11个地市2023年地区生产总值占比的分位数为,C错误.
若该省2024年各地市地区生产总值的增长率相等,则该省2024年各地市地区生产总值的占比不变,D正确.
11.答案:ABD
解析:2021年12月份我国规模以上工业天然气产量当月增速为2.3个百分点,11月份增速为4.4个百分点,比上月放缓2.1个百分点.故A正确;
2021年4月至12月我国规模以上工业天然气产量当月增速的极差为.故B正确;
2021年7月我国规模以上工业天然气产量为亿立方米.故C错误
2021年4月至12月我国规模以上工业天然气日均产量从小到大为5.1,5.1,5.2,5.3,5.4,5.6,5.7,5.9,6.2,因为,所以该组数据的40%分位数为5.3亿立方米.故D正确
故选:ABD.
12.答案:5
解析:因为a,b是方程的两根,解得或4,
不妨设,,则样本平均数为,
由方差公式得.
故答案为:5.
13.答案:6720
解析:在随机抽取的50人中,持反对态度的频率为,
则可估计该地区对“键盘侠”持反对态度的有(人).
故答案为:6720.
14.答案:①②④
解析:总体容量为4500,样本容量为90,所以抽样比为,所以样本中男生的人数为,①正确;
对于有限n次随机试验,事件A发生的频率是随机的,而随机试验次数n趋向无穷大,随机事件A发生的频率会逐渐稳定于事件A发生的概率,②正确;
数据4,8,10,14的平均数,方差,
数据2,4,5,7的平均数,方差为,
则,故数据4,8,10,14的方差是2,4,5,7的方差的4倍,③错误;
基本事件有“取出的两球均为红球”,“取出的两球均为白球”,“取出的球为一红球和一白球”等,因此事件A与B互斥而不对立,④正确;
故正确命题的编号为①②④.
故答案为:①②④.
15.答案:(1)1030;
(2),应选择方案二
解析:(1)临界值时,I级品中该指标大于60的频率为,
II级品中该指标大于60的频率为0.1
故该公司生产的1000个该型号芯片I级品和1000个II级品中应用于A型手机的芯片个数估计为:
(2)当临界值时,若采用方案一:
I级品中该指标小于或等于临界值K的概章为,可以估计10000部A型手机中有部手机芯片应用错误;
II级品中该指标大于临界值K的概率为,
可以估计10000部B型手机中有部手机芯片应用错误;
故可以估计芯片生产商的损失费用
,
又采用方案二需要检测费用共130万元
故从芯片生产商的成本考虑,应选择方案二
16.答案:(1)84.7;
(2)分布列见解析,;
(3)
解析:(1)因为,,
所以中位数位于之间,设中位数为x,则,
解得.
(2)依题意可得X的可能取值为0,1,2,3,
,,
,,
X的分布列如下:
X 0 1 2 3
P
所以.
(3)由频率分布直方图可知员工考核是良好的频率为,
合格的频率为,
不合格的频率为,
记事件A为“该员工复评晋级”,事件B为“该员工初评是合格”,
则.
17.答案:(1);
(2)分布列见解析,
解析:(1)由频率分布直方图得:.解得;
(2)由频率分布直方图得:
这1000名学生中日平均阅读时间在,两组内的学生人数之比为,
若采用分层抽样的方法抽取了10人,则从日平均阅读时间在内的学生中抽取(人)
在日平均阅读时间在内的学生中抽取4人,
现从这10人中随机拍取3人,则X服从超几何分布,其可能取值为0,1,2,3,
,,
,,
X的分布列为:
X 0 1 2 3
P
.
18.答案:(1)这批零件的长度大于1.60分米的频率为0.15;,,
(2)X的分布列见解析;数学期望为2.1
(3)这批零件是合格的,将顺利被该公司签收
解析:(1)由题意可知120个样本零件中长度大于1.60分米的共有18个,
则这批零件的长度大于1.60分米的频率为.
记Y为零件的长度,
则,
,
,
故,,.
(2)由(1)可知从这批零件中随机选取1个,长度在的概率.
又随机变量X服从二项分布,
则,
,
,
,
故随机变量X的分布列为
X 0 1 2 3
P 0.027 0.189 0.441 0.343
(或).
(3)由题意可知,,
则,
.
因为,,
所以这批零件的长度满足近似于正态分布的概率分布.
因此应认为这批零件是合格的,将顺利被该公司签收.
19.答案:(1)见解析
(2)分布列见解析,
解析:(1)补充列联表如下所示:
药物 疗效 合计
治愈 未治愈
创新药 40 10 50
传统药 280 120 400
合计 320 130 450
因为,所以根据小概率值的独立性检验,创新药的疗效没有比传统药好;
(2)按疗效比例分层随机抽取10名,则有7名治愈者和3名未治愈者,要求抽取8人回访,所以,6,5,则,,,故分布列为:
X 7 6 5
P
均值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2024-2025学年人教A版必修二单元测试:第九章 统计
一、选择题
1.从小到大排列的数据1,2,3,5,6,7,8,9,10,14,15,18的下四分位数为( )
A.3 B.4 C.10 D.12
2.某校高一年级有男生300人,女生200人,按性别进行分层,用分层随机抽样的方法从该校高一年级学生中抽出一个容量为150的样本.如果样本按比例分配,那么男生、女生应分别抽取的人数为( )
A.75;75 B.90;60 C.60;90 D.100;50
3.“幸福感指数”是指人们主观地评价自己目前生活状态的满意程度的指标,常用区间内的一个数来表示,该数越接近10表示满意程度越高.现随机抽取10位某小区居民,他们的幸福感指数分别为3,4,5,5,6,6,7,8,9,10,则这组数据的第80百分位数是( )
A.7.5 B.8 C.8.5 D.9
4.下列说法不正确的是( )
A.一组数据10,11,11,12,13,14,16,18,20,22的第60百分位数为14
B.若随机变量X服从正态分布,且,则
C.若线性相关系数越接近1,则两个变量的线性相关程度越高
D.对具有线性相关关系的变量x、y,且回归方程为,若样本点的中心为,则实数m的值是
5.已知某学校高三年级甲、乙、丙三个班级人数分别为40,30,50,学校计划采用按比例分配的分层随机抽样的方法在三个班级中评选优秀学生,已知乙班分配到的优秀学生名单为6人,则高三年级三个班优秀学生总人数为( )
A.16 B.30 C.24 D.18
6.已知样本数据10,11,9,13,10,9,12,则这组样本数据的上四分位数为( )
A.9 B.10 C.11 D.12
7.甲、乙两个跑步爱好者利用微信运动记录了去年下半年每个月的跑步里程(单位:公里),现将两人的数据绘制成如图所示的折线图,则下列结论中错误的是( )
A.甲跑步里程的极差等于110
B.乙跑步里程的中位数是273
C.分别记甲、乙下半年每月跑步里程的平均数为,,则
D.分别记甲乙下半年每月跑步里程的标准差为,,则
8.有一组样本数据:15,16,11,11,14,20,11,13,13,24,13,18,则这组样本数据的上四分位数是( )
A.11 B.12 C.16 D.17
二、多项选择题
9.下列说法正确的是( )
A.已知随机变量X服从二项分布,则
B.设随机变量X服从正态分布,若,则
C.已知一组数据为1,2,3,4,5,6,7,8,9,10,则它的第70百分位数为7
D.若事件A,B满足,,,则事件A,B相互独立
10.已知某省2023年各地市地区生产总值的占比如图所示,则根据图中关于该省2023年各地市地区生产总值占比的统计情况,下列结论正确的是( )
A.A市2023年地区生产总值比B市2023年地区生产总值多
B.图中11个地市2023年地区生产总值占比的分位数为
C.图中11个地市2023年地区生产总值占比的分位数为
D.若该省2024年各地市地区生产总值的增长率相等,则该省2024年各地市地区生产总值的占比不变
11.2021年4月至2021年12月我国规模以上工业天然气产量保持平稳,日均产量(亿立方米)与当月增速(%)如图所示,则( )
备注:日均产品产量是以当月公布的我国规模以上工业企业总产量除以该月日历天数计算得到.
当月增速.
A.2021年12月份我国规模以上工业天然气产量当月增速比上月放缓2.1个百分点
B.2021年4月至2021年12月我国规模以上工业天然气产量当月增速的极差为12.6%
C.2021年7月份我国规模以上工业天然气产量为153亿立方米
D.2021年4月至2021年12月我国规模以上工业天然气日均产量的40%分位数为5.3亿立方米
三、填空题
12.一组样本数据为1,a,4,5,b,8,若a,b是方程的两根,则这个样本的方差是___________.
13.“键盘侠”一词描述了部分网民在现实生活中胆小怕事、自私自利,却习惯在网络上大放厥词的一种现象.某地新闻栏目对该地区群众对“键盘侠”的认可程度进行调查:在随机抽取的50人中,有15人持认可态度,其余持反对态度,若该地区有9600人,则可估计该地区对“键盘侠”持反对态度的有__________人.
14.下列命题中:
①某校共有男生2700人,女生1800人,用比例分配的分层随机抽样抽取容量为90的样本进行健康测试,则样本中男生有54人;
②随着试验次数n的增大,一个随机事件A发生的频率会逐渐稳定于事件A发生的概率;
③数据4,8,10,14的方差是2,4,5,7的方差的2倍;
④从3个红球和2个白球中任取两个球,记事件“取出的两球均为红球”,事件“取出的两个球颜色不同”,则事件A与B互斥而不对立;
其中正确命题的编号为__________.
四、解答题
15.已知某科技公司的某型号芯片的各项指标经过全面检测后,分为I级和Ⅱ级,两种品级芯片的某项指标的频率分布直方图如图所示:
若只利用该指标制定一个标准,需要确定临界值K,将该指标大于K的产品应用于A型手机,小于或等于K的产品应用于B型手机.假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率.
(1)若临界值,请估计该公司生产的1000个该型号芯片I级品和1000个Ⅱ级品中应用于A型手机的芯片个数;
(2)设且,现有足够多的芯片I级品 Ⅱ级品,分别应用于A型手机 B型手机各1万部的生产:
方案一:直接将该芯片I级品应用于A型手机,其中该指标小于等于临界值K的芯片会导致芯片生产商每部手机损失800元;直接将该芯片Ⅱ级品应用于B型手机,其中该指标大于临界值K的芯片,会导致芯片生产商每部手机损失400元;
方案二:重新检测芯片I级品,II级品的该项指标,并按规定正确应用于手机型号,会避免方案一的损失费用,但检测费用共需要130万元;
请求出按方案一,芯片生产商损失费用的估计值(单位:万元)的表达式,并从芯片生产商的成本考虑,选择合理的方案.
16.某企业为激发员工的工作热情,年终对职工进行绩效考核,按绩效发放年终奖,将评价结果采用百分制进行了初评,并根据员工得分绘制出下面的频率分布直方图,评分在区间直接定为优秀,评分在区间,,,分别对应为良好、合格、不合格.然后又对良好、合格、不合格的员工再进行一次复评.在复评中,原来评为良好、合格、不合格员工都有的概率提升一级,分别变为优秀、良好、合格,不晋级则保留原等级,每位员工的复评结果相互独立.
(1)估计该企业初评成绩的中位数;(结果精确到0.1)
(2)在初评中甲、乙、丙三人分别获得良好、合格、合格,记三人复评后为良好等级的人数为X,求X的分布列和数学期望;
(3)从全体员工中任选1人,求在已知该员工是复评后晋级的条件下,初评是合格的概率.
17.每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”,为了解某地区高一学生阅读时间的分配情况,从该地区随机抽取了1000名高一学生进行在线调查,得到了这1000名学生的日平均阅读时间(单位:小时),并将样本数据分成,,,,,,,,九组,绘制成如图所示的频率分布直方图.
(1)求a的值:
(2)为进一步了解这1000名学生数字媒体阅读时间和纸质图书阅读时间的分配情况,从日平均阅读时间在,两组内的学生中,采用分层抽样的方法抽取了10人,现从这10人中随机抽取3人,记日平均阅读时间在内的学生人数为X,求X的分布列和数学期望.
18.某公司采购了一批零件,为了检测这批零件是否合格,从中随机抽测120个零件的长度(单位:分米),将数据分成,,,,,这6组,得到如图的频率分布直方图,其中长度大于或等于1.59分米的零件有20个,其长度分别为1.59,1.59,1.61,1.61,1.62,1.63,1.63,1.64,1.65,1.65,1.65,1.65,1.66,1.67,1.68,1.69,1.69,1.71,1.72,1.74.以这120个零件在各组的长度的频率估计整批零件在各组长度的概率.
(1)求这批零件的长度大于1.60分米的频率,并求频率分布直方图中m,n,t的值.
(2)若从这批零件中随机选取3个,记X为抽取的零件长度在的个数,求X的分布列和数学期望.
(3)若变量S满足且,则称变量S满足近似于正态分布的概率分布.如果这批零件的长度Y满足近似于正态分布的概率分布,则认为这批零件是合格的将顺利被签收,否则,公司将拒绝签收.试问:该批零件能否被签收?
19.治疗某种疾病有一种传统药和一种创新药,治疗效果对比试验数据如下:服用创新药的50名患者中有40名治愈;服用传统药的400名患者中有120名未治愈.
(1)补全列联表(单位:人),并根据小概率值的独立性检验,分析创新药的疗效是否比传统药好;
药物 疗效 合计
治愈 未治愈
创新药
传统药
合计
(2)从服用传统药的400名患者中按疗效比例分层随机抽取10名,在这10人中随机抽取8人进行回访,用X表示回访中治愈者的人数,求X的分布列及均值.
附:,
参考答案
1.答案:B
解析:数据共12个,,
故从小到大,选择第3和第4个数的平均数作为下四分位数,即.
故选:B.
2.答案:B
解析:由题意可得,样本中应抽取的男生有名,
样本中应抽取的男生有名.
故选:B.
3.答案:C
解析:因为,
所以第80百分位数是.
故选:C
4.答案:A
解析:对A:因为,所以第60百分位数为,A错误;
对B:若随机变量X服从正态分布,且,
则,
则,B正确;
对C:若线性相关系数越接近1,则两个变量的线性相关性越强,C正确;
对于D,样本点的中心为,所以,,
因为满足线性回归方程,所以,所以,D正确.
故选:A.
5.答案:C
解析:甲、乙、丙三个班级人数比为,由分层随机抽样知,三个班级优秀学生名额分别为8,6,10,
所以高三年级三个班优秀学生总人数为人.
故选:C
6.答案:D
解析:将样本数据按从小到大的顺序排列为:9,9,10,10,11,12,13.
上四分位数即75%分位数,,
所以该组数据的上四分位数为从小到大排列的第6个数,即12,
故选:D.
7.答案:C
解析:
8.答案:D
解析:将样本数据由小到大排列依次为:11,11,11,13,13,13,14,15,16,18,20,24,
因为上四分位数是第分位数,则,所以这组数据的上四分位数为.
故选:D.
9.答案:AD
解析:因为随机变量X服从二项分布,则,故A正确;
因为随机变量X服从正态分布,则对称轴为,,故B错误;
这组数据的第70百分位数为,故C错误;
因为,所以,所以事件A,B相互独立.
故选:AD.
10.答案:ABD
解析:由图中统计数据,可得A市2023年地区生产总值比B市2023年地区生产总值多,A正确.
因为,所以图中11个地市2023年地区生产总值占比的分位数为,B正确.
因为,所以图中11个地市2023年地区生产总值占比的分位数为,C错误.
若该省2024年各地市地区生产总值的增长率相等,则该省2024年各地市地区生产总值的占比不变,D正确.
11.答案:ABD
解析:2021年12月份我国规模以上工业天然气产量当月增速为2.3个百分点,11月份增速为4.4个百分点,比上月放缓2.1个百分点.故A正确;
2021年4月至12月我国规模以上工业天然气产量当月增速的极差为.故B正确;
2021年7月我国规模以上工业天然气产量为亿立方米.故C错误
2021年4月至12月我国规模以上工业天然气日均产量从小到大为5.1,5.1,5.2,5.3,5.4,5.6,5.7,5.9,6.2,因为,所以该组数据的40%分位数为5.3亿立方米.故D正确
故选:ABD.
12.答案:5
解析:因为a,b是方程的两根,解得或4,
不妨设,,则样本平均数为,
由方差公式得.
故答案为:5.
13.答案:6720
解析:在随机抽取的50人中,持反对态度的频率为,
则可估计该地区对“键盘侠”持反对态度的有(人).
故答案为:6720.
14.答案:①②④
解析:总体容量为4500,样本容量为90,所以抽样比为,所以样本中男生的人数为,①正确;
对于有限n次随机试验,事件A发生的频率是随机的,而随机试验次数n趋向无穷大,随机事件A发生的频率会逐渐稳定于事件A发生的概率,②正确;
数据4,8,10,14的平均数,方差,
数据2,4,5,7的平均数,方差为,
则,故数据4,8,10,14的方差是2,4,5,7的方差的4倍,③错误;
基本事件有“取出的两球均为红球”,“取出的两球均为白球”,“取出的球为一红球和一白球”等,因此事件A与B互斥而不对立,④正确;
故正确命题的编号为①②④.
故答案为:①②④.
15.答案:(1)1030;
(2),应选择方案二
解析:(1)临界值时,I级品中该指标大于60的频率为,
II级品中该指标大于60的频率为0.1
故该公司生产的1000个该型号芯片I级品和1000个II级品中应用于A型手机的芯片个数估计为:
(2)当临界值时,若采用方案一:
I级品中该指标小于或等于临界值K的概章为,可以估计10000部A型手机中有部手机芯片应用错误;
II级品中该指标大于临界值K的概率为,
可以估计10000部B型手机中有部手机芯片应用错误;
故可以估计芯片生产商的损失费用
,
又采用方案二需要检测费用共130万元
故从芯片生产商的成本考虑,应选择方案二
16.答案:(1)84.7;
(2)分布列见解析,;
(3)
解析:(1)因为,,
所以中位数位于之间,设中位数为x,则,
解得.
(2)依题意可得X的可能取值为0,1,2,3,
,,
,,
X的分布列如下:
X 0 1 2 3
P
所以.
(3)由频率分布直方图可知员工考核是良好的频率为,
合格的频率为,
不合格的频率为,
记事件A为“该员工复评晋级”,事件B为“该员工初评是合格”,
则.
17.答案:(1);
(2)分布列见解析,
解析:(1)由频率分布直方图得:.解得;
(2)由频率分布直方图得:
这1000名学生中日平均阅读时间在,两组内的学生人数之比为,
若采用分层抽样的方法抽取了10人,则从日平均阅读时间在内的学生中抽取(人)
在日平均阅读时间在内的学生中抽取4人,
现从这10人中随机拍取3人,则X服从超几何分布,其可能取值为0,1,2,3,
,,
,,
X的分布列为:
X 0 1 2 3
P
.
18.答案:(1)这批零件的长度大于1.60分米的频率为0.15;,,
(2)X的分布列见解析;数学期望为2.1
(3)这批零件是合格的,将顺利被该公司签收
解析:(1)由题意可知120个样本零件中长度大于1.60分米的共有18个,
则这批零件的长度大于1.60分米的频率为.
记Y为零件的长度,
则,
,
,
故,,.
(2)由(1)可知从这批零件中随机选取1个,长度在的概率.
又随机变量X服从二项分布,
则,
,
,
,
故随机变量X的分布列为
X 0 1 2 3
P 0.027 0.189 0.441 0.343
(或).
(3)由题意可知,,
则,
.
因为,,
所以这批零件的长度满足近似于正态分布的概率分布.
因此应认为这批零件是合格的,将顺利被该公司签收.
19.答案:(1)见解析
(2)分布列见解析,
解析:(1)补充列联表如下所示:
药物 疗效 合计
治愈 未治愈
创新药 40 10 50
传统药 280 120 400
合计 320 130 450
因为,所以根据小概率值的独立性检验,创新药的疗效没有比传统药好;
(2)按疗效比例分层随机抽取10名,则有7名治愈者和3名未治愈者,要求抽取8人回访,所以,6,5,则,,,故分布列为:
X 7 6 5
P
均值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
