优课沪科版初中数学八年级上册第12章函数综合练习(共23张PPT)
文档属性
| 名称 | 优课沪科版初中数学八年级上册第12章函数综合练习(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 516.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-28 16:13:01 | ||
图片预览





文档简介
课件23张PPT。
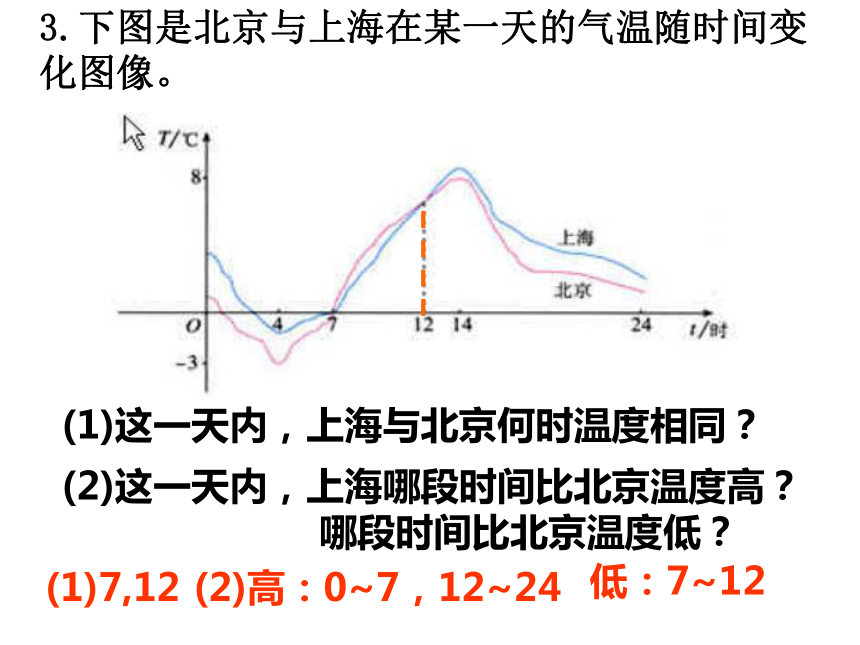
12.1函数综合练习复习检测1. 一般地,对于一个函数,把自变量x与函数y的每对对应值分别作为点的( ),在坐标平面内找出相应的点,由这些点组成的图形,就叫做这个函数的图象。这种表示函数的方法叫做( )2.作函数图象的一般步骤?横坐标和纵坐标图象法(1)列表 (2)描点 (3)连线3.下图是北京与上海在某一天的气温随时间变化图像。(1)这一天内,上海与北京何时温度相同?(2)这一天内,上海哪段时间比北京温度高?
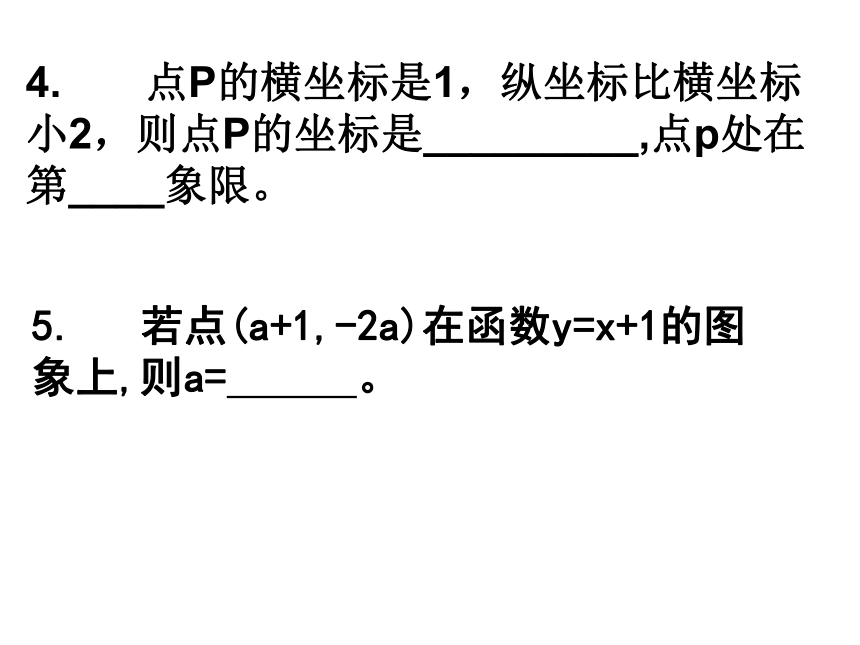
哪段时间比北京温度低?(1)7,12(2)高:0~7,12~24低:7~125. 若点(a+1,-2a)在函数y=x+1的图象上,则a= 。4. 点P的横坐标是1,纵坐标比横坐标小2,则点P的坐标是_________,点p处在第____象限。例: 一水库的水位在最近5小时内持续上涨, 下表记录了这5小时的水位高度。例题解析(1)由记录表推出这5小时中水位高度y随时间t变化的函数解析式;(2)据估计这种上涨情况还会持续2小时,预测再过2小时水位高度将达到多少米,并画出函数图像。分析: 记录表中的6组数值反映了时间t与水位y之间的对应关系,从这些数值中可以找出这两个变量之间的一般联系规律,由它写出函数解析式,画出函数图像,进而预测水位。解: (1)由表观察到开始水位高10米,以后
每隔1小时,水位升高0.05米,这样的变化
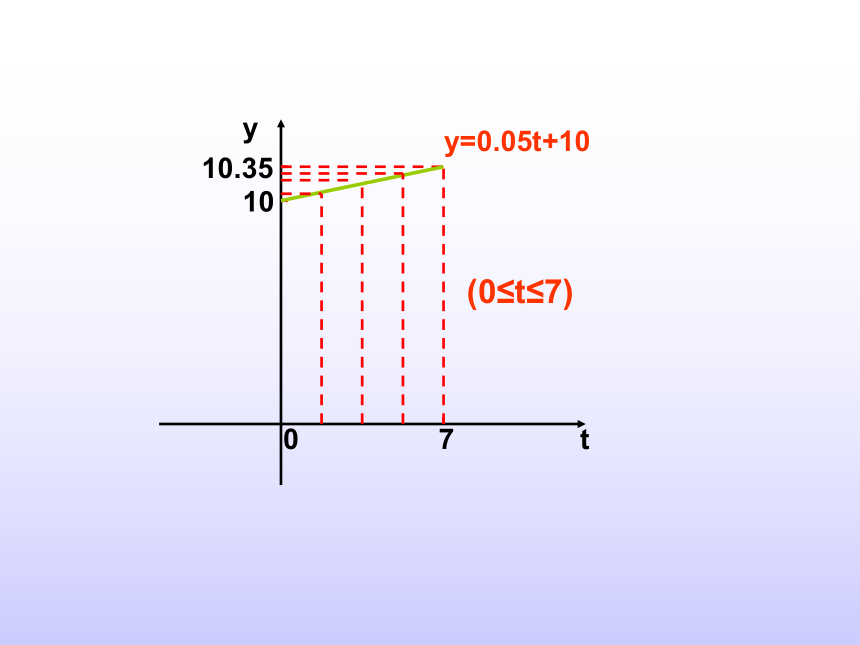
规律可以表示为:y=0.05t+10(0≤t≤7)(2)再过两小时的水位高度,就是t=5+2=7时
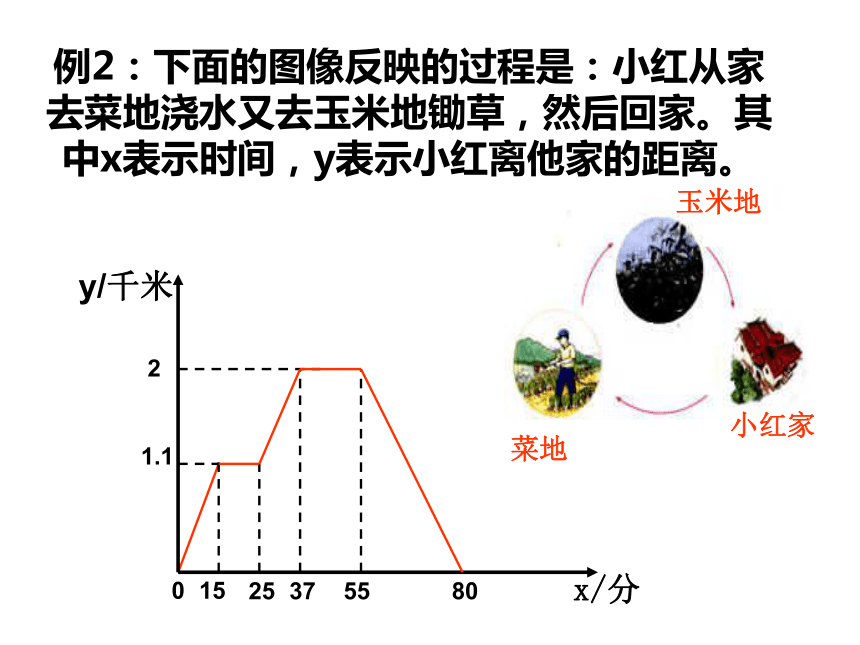
y=0.05t+10的函数值,从解析式容易算出y=0.05×7+10=10.35两小时后估计水位高10.35 米画函数图像:710.35100yt(0≤t≤7)y=0.05t+10例2:下面的图像反映的过程是:小红从家
去菜地浇水又去玉米地锄草,然后回家。其
中x表示时间,y表示小红离他家的距离。y/千米1.12玉米地菜地小红家根据图像回答下列问题:(1)菜地离小红家多远?小红走到菜地用了
多少时间?(2)小红给菜地浇水用了多少时间?(3)菜地离玉米地多远?小红从菜地到玉米
地用了多少时间?(4)小红给玉米地锄草用了多少时间?(5)玉米地离小红家多远?小红从玉米地
走回家的平均速度是多少?分析:小红离家的距离y是时间x的函数,
从图像中有两段是平行于x轴的线段可知,
小红离家后又两段时间内先后停留在菜
地与玉米地。y/千米1.12解: (1)由纵坐标看出,菜地离小红家1.1千米;
由横坐标看出,小红走到菜地用了15分钟。(2) 25-15=10(分),小红给菜地浇水用了10分。(3)2-1.1=0.9(千米),菜地离玉米地0.9 千米;
37-25=12(分),小红从菜地到玉米地用了12分。(4)55-37=18(分),小红给玉米地锄草用了18分。y/千米1.12(5)由纵坐标看出,玉米地离小红家2千米;
80-55=25(分)平均速度为:2÷25=0.08(千米/分)玉米地到小红家用时:y/千米1.12当堂检测1.一天,亮亮感冒发烧了,早晨他烧得厉害,吃过药后感冒好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么发烫了.图中能基本反映出亮亮这一天(0~24时)体温的变化情况的是C2.某产品的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3小时后安排工人装箱,若每小时装产品150件,未装箱的产品数量为y,生产时间为t,那么y与t的大致图象只能是A3.如图,向高为H的圆柱形空水杯里注水,
表示注水量y与水深x的关系的图象是( )
B4.一辆公共汽车从车站开出,加速行驶一段后开始
匀速行驶,过了一段时间,汽车到了下一个车站,
乘客上下车后汽车开始加速,一段时间后又开始匀
速行驶,则图中近似地刻画出汽车在这段时间内的
速度变化情况的是( )
B5. 已知点A(3, 2)在函数y=2x+m的图象上,试判断B(-2,-8)是否在函数图象上。6. 已知函数y=2x-3,求:
(1)函数图象与x轴、y轴的交点坐标. (2)函数图象与函数y=x+1的图象的交点坐标.7.下列图象关系中, 是 的函数吗?是不是.拓展提升 某公司到果园基地购买优质水果慰问医务工作者,果园基地对购买量在3000KG以上(含3000KG)的有两种销售方案,甲方案:每千克9元,由果园基地送货上门。乙方案:每千克8元,由顾客自己租车到果园。已知该公司到该果园基地的运输费用为5000元。
(1)分别写出该公司采用两种购买方案时应付y元与所买水果xkg之间函数关系式,并写出自变量取值范围;
(2)当购买量在某一范围时,选择哪种购买方案,付款最少?并说明理由谈谈本节课你有何收获?
哪段时间比北京温度低?(1)7,12(2)高:0~7,12~24低:7~125. 若点(a+1,-2a)在函数y=x+1的图象上,则a= 。4. 点P的横坐标是1,纵坐标比横坐标小2,则点P的坐标是_________,点p处在第____象限。例: 一水库的水位在最近5小时内持续上涨, 下表记录了这5小时的水位高度。例题解析(1)由记录表推出这5小时中水位高度y随时间t变化的函数解析式;(2)据估计这种上涨情况还会持续2小时,预测再过2小时水位高度将达到多少米,并画出函数图像。分析: 记录表中的6组数值反映了时间t与水位y之间的对应关系,从这些数值中可以找出这两个变量之间的一般联系规律,由它写出函数解析式,画出函数图像,进而预测水位。解: (1)由表观察到开始水位高10米,以后
每隔1小时,水位升高0.05米,这样的变化
规律可以表示为:y=0.05t+10(0≤t≤7)(2)再过两小时的水位高度,就是t=5+2=7时
y=0.05t+10的函数值,从解析式容易算出y=0.05×7+10=10.35两小时后估计水位高10.35 米画函数图像:710.35100yt(0≤t≤7)y=0.05t+10例2:下面的图像反映的过程是:小红从家
去菜地浇水又去玉米地锄草,然后回家。其
中x表示时间,y表示小红离他家的距离。y/千米1.12玉米地菜地小红家根据图像回答下列问题:(1)菜地离小红家多远?小红走到菜地用了
多少时间?(2)小红给菜地浇水用了多少时间?(3)菜地离玉米地多远?小红从菜地到玉米
地用了多少时间?(4)小红给玉米地锄草用了多少时间?(5)玉米地离小红家多远?小红从玉米地
走回家的平均速度是多少?分析:小红离家的距离y是时间x的函数,
从图像中有两段是平行于x轴的线段可知,
小红离家后又两段时间内先后停留在菜
地与玉米地。y/千米1.12解: (1)由纵坐标看出,菜地离小红家1.1千米;
由横坐标看出,小红走到菜地用了15分钟。(2) 25-15=10(分),小红给菜地浇水用了10分。(3)2-1.1=0.9(千米),菜地离玉米地0.9 千米;
37-25=12(分),小红从菜地到玉米地用了12分。(4)55-37=18(分),小红给玉米地锄草用了18分。y/千米1.12(5)由纵坐标看出,玉米地离小红家2千米;
80-55=25(分)平均速度为:2÷25=0.08(千米/分)玉米地到小红家用时:y/千米1.12当堂检测1.一天,亮亮感冒发烧了,早晨他烧得厉害,吃过药后感冒好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么发烫了.图中能基本反映出亮亮这一天(0~24时)体温的变化情况的是C2.某产品的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3小时后安排工人装箱,若每小时装产品150件,未装箱的产品数量为y,生产时间为t,那么y与t的大致图象只能是A3.如图,向高为H的圆柱形空水杯里注水,
表示注水量y与水深x的关系的图象是( )
B4.一辆公共汽车从车站开出,加速行驶一段后开始
匀速行驶,过了一段时间,汽车到了下一个车站,
乘客上下车后汽车开始加速,一段时间后又开始匀
速行驶,则图中近似地刻画出汽车在这段时间内的
速度变化情况的是( )
B5. 已知点A(3, 2)在函数y=2x+m的图象上,试判断B(-2,-8)是否在函数图象上。6. 已知函数y=2x-3,求:
(1)函数图象与x轴、y轴的交点坐标. (2)函数图象与函数y=x+1的图象的交点坐标.7.下列图象关系中, 是 的函数吗?是不是.拓展提升 某公司到果园基地购买优质水果慰问医务工作者,果园基地对购买量在3000KG以上(含3000KG)的有两种销售方案,甲方案:每千克9元,由果园基地送货上门。乙方案:每千克8元,由顾客自己租车到果园。已知该公司到该果园基地的运输费用为5000元。
(1)分别写出该公司采用两种购买方案时应付y元与所买水果xkg之间函数关系式,并写出自变量取值范围;
(2)当购买量在某一范围时,选择哪种购买方案,付款最少?并说明理由谈谈本节课你有何收获?
