湖南省长沙市湖南师大附中博才实验中学2024-2025学年九年级上学期入学考试数学试卷(pdf版,无答案)
文档属性
| 名称 | 湖南省长沙市湖南师大附中博才实验中学2024-2025学年九年级上学期入学考试数学试卷(pdf版,无答案) |  | |
| 格式 | |||
| 文件大小 | 419.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-17 08:19:24 | ||
图片预览

文档简介
数学作业
班级:___________ 学号:___________ 姓名:___________
一、选择题(本题共 10 小题,每题 3 分,共 30 分)
1.已知△ABC中∠A、∠B、∠C的对边分别是 a、b、c,下列条件不能判定△ABC是直角三角形的是( )
A.b2 c2 = a2 B. a = 2 ,b = 3 , c = 5
C. A + B = C D. A : B : C = 3: 4 : 5
2
2.对于二次函数 y = (x 1) + 2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是 x = 1 C.顶点坐标是 (1,2) D.与 x轴有两个交点
3.如图,在菱形 ABCD中,E、F分别是 AC、AB的中点,如果 EF = 3,
D A
那么菱形 ABCD的周长为( )
F
A.24 B.18 E
C.12 D.9 C B
4.若 2x1, x2是一元二次方程 x + x 2 = 0的两个实数根,则 x1 + x2 4x1x2 的值为( )
A.4 B. 3 C.0 D.7
5.对于一次函数 y = 2x + 4,下列说法错误的是( )
A.y随 x的增大而减小 B.图象与 y轴交点为 (0,4)
C.图象经过第一、二、四象限 D.图象经过点 (1,3)
6.六位同学的年龄分别是 13、14、15、14、14、15 岁,关于这组数据,正确说法是( )
A.平均数是 14 B.众数是 14 C.方差是 3 D.中位数是14.5
7.关于 x的一元二次方程 x2 6x + m = 0 有两个不相等的实数根,则 m的值可能是( )
A.8 B.9 C.10 D.11
8.如图,在矩形 ABCD中,对角线 AC,BD相交于点 O,若 OAD = 40 ,
A D
则∠COD的度数为( )
A.20° B.40° O
C.80° D.100° B C
9.随着中考结束,初三某毕业班的每一个同学都向其他同学赠送一张自己的照片留作纪念,全班共送了 2256
张照片,若该班有 x名同学,则根据题意可列出方程为( )
1
A. x(x 1) = 2256 B. x(x +1) = 2256 C. 2x(x 1) = 2256 D. x (x 1) = 2256
2
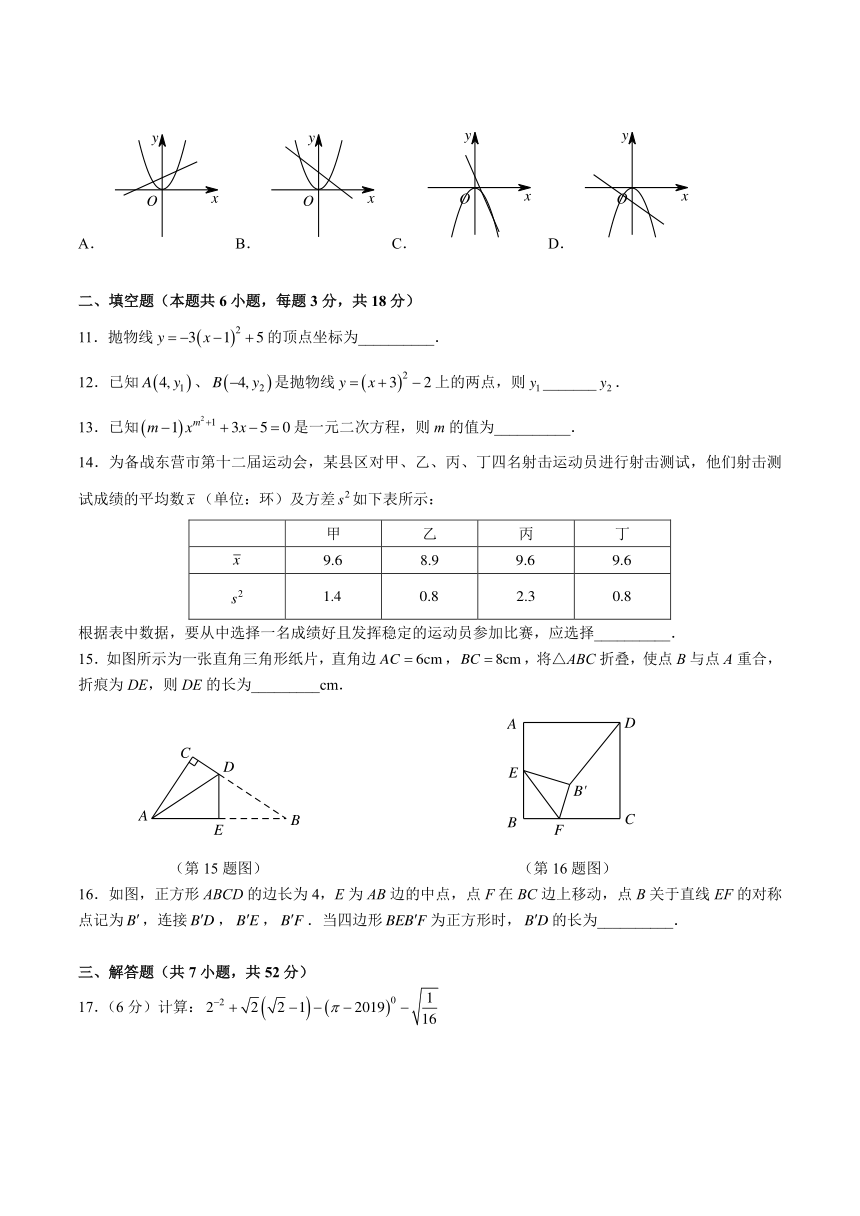
10.函数 y = ax2 与 y = ax + b 的图象可能是( )
{#{QQABACYCAgwggAAwAgptSBAACAZB5hLCEEwwGGoYCCggiQGsQJEkBiJGcgCkChYRgCGLROBAA4DEIgAINIBAgBINAA=}B#A} A=}#}
y y y y
O x O x O x O x
A. B. C. D.
二、填空题(本题共 6 小题,每题 3 分,共 18 分)
2
11.抛物线 y = 3(x 1) + 5 的顶点坐标为__________.
2
12.已知 A(4, y1 )、 B ( 4, y2 )是抛物线 y = (x + 3) 2 上的两点,则 y1 _______ y2 .
2
.已知 (m 1) xm +113 + 3x 5 = 0 是一元二次方程,则 m的值为__________.
14.为备战东营市第十二届运动会,某县区对甲、乙、丙、丁四名射击运动员进行射击测试,他们射击测
试成绩的平均数 x (单位:环)及方差 s2 如下表所示:
甲 乙 丙 丁
x 9.6 8.9 9.6 9.6
s2 1.4 0.8 2.3 0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择__________.
15.如图所示为一张直角三角形纸片,直角边 AC = 6cm,BC = 8cm,将△ABC折叠,使点 B与点 A重合,
折痕为 DE,则 DE的长为_________cm.
A D
C
D E
B'
A B B C
E F
(第 15 题图) (第 16 题图)
16.如图,正方形 ABCD的边长为 4,E为 AB边的中点,点 F在 BC边上移动,点 B关于直线 EF的对称
点记为 B ,连接 B D , B E , B F .当四边形 BEB F 为正方形时, B D 的长为__________.
三、解答题(共 7 小题,共 52 分)
0 1
17.(6 分)计算: 2 2 + 2 ( 2 1) ( 2019)
16
{#{QQABCAYCAgwggAAwAgptSBAACAZB5hLCEEwwGGoYCCggiQGsQJEkBiJGcgCkChYRgCGLROBAA4DEIgAINIBAgBINAA=}B#A} A=}#}
18.(6 分)解方程
2
(1) (x 2) 9 = 0 (2) x2 + 2x = 3
2
19.(6 分)已知抛物线 y = a (x 1) + h 经过点 (0, 3)和 (3,0).
(1)求 a、h的值;
(2)将该抛物线向上平移 2 个单位长度,再向右平移 1 个单位长度,得到新的抛物线,直接写出新的抛物
线相应的函数表达式.
20.(8 分)如图,在△ABC中, C = 90 ,BD平分∠ABC交 AC于点 D,过 D作 DE∥BC交 AB于点 E,
DF∥AB交 BC于点 F,连接 EF.
(1)求证:四边形 BFDE是菱形;
(2)若 AB = 8, AD = 4 ,求 BF的长.
A
E D
B C
F
{#{QQABCAYCAgwggAAwAgptSBAACAZB5hLCEEwwGGoYCCggiQGsQJEkBiJGcgCkChYRgCGLROBAA4DEIgAINIBAgBINAA=}B#A} A=}#}
21.(8 分)如图,直线 y = 3x + 6 交 x轴和 y轴于点 A和点 B,点C (0, 3)在 y轴上,连接 AC.
(1)求点 A和点 B的坐标;
(2)若点 P是直线 AB上一点,若△BCP的面积为 18,求点 P的坐标.
y
B
A
O x
C
22.(9 分)某县著名传统土特产品“豆笋”“豆干”以“浓郁豆香,绿色健康”享誉全国,深受广大消费者
喜爱.已知 2 件豆笋和 3 件豆干进货价为 240 元,3 件豆笋和 4 件豆干进货价为 340 元.
(1)分别求出每件豆笋、豆干的进价.
3
(2)某特产店计划用不超过 10440 元购进豆笋、豆干共 200 件,且豆笋的数量不低于豆干数量的 ,该特
2
产店有哪几种进货方案?
(3)若该特产店每件豆笋售价为 80 元,每件豆干售价为 55 元,在(2)的条件下,怎样进货可使该特产
店获得利润最大,最大利润为多少元?
{#{QQABACYCAgwggAAwAgptSBAACAZB5hLCEEwwGGoYCCggiQGsQJEkBiJGcgCkChYRgCGLROBAA4DEIgAINIBAgBINAA=}B#A} A=}#}
23.(9 分)定义:对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点
四边形”,如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”
【概念理解】
(1)在已经学过的“①平行四边形;②矩形;③菱形;④正方形”中,_________是“中方四边形”(填序
号).
【性质探究】
(2)如图 1,若四边形 ABCD是“中方四边形”,观察图形,线段 AC和线段 BD有什么关系,并证明你的
结论.
【问题解决】
(3)如图 2,以锐角△ABC的两边 AB,AC为边长,分别向外侧作正方形 ABDE和正方形 ACFG连结 BE,
EG,GC,依次连接四边形 BCGE的四边中点得到四边形 MNRL.求证:四边形 BCGE是“中方四边形”.
A
G
H
E
F
E A
B D
F G D
C B C
图 1 图 2
{#{QQABACYCAgwggAAwAgptSBAACAZB5hLCEEwwGGoYCCggiQGsQJEkBiJGcgCkChYRgCGLROBAA4DEIgAINIBAgBINAA=}B#A} A=}#}
班级:___________ 学号:___________ 姓名:___________
一、选择题(本题共 10 小题,每题 3 分,共 30 分)
1.已知△ABC中∠A、∠B、∠C的对边分别是 a、b、c,下列条件不能判定△ABC是直角三角形的是( )
A.b2 c2 = a2 B. a = 2 ,b = 3 , c = 5
C. A + B = C D. A : B : C = 3: 4 : 5
2
2.对于二次函数 y = (x 1) + 2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是 x = 1 C.顶点坐标是 (1,2) D.与 x轴有两个交点
3.如图,在菱形 ABCD中,E、F分别是 AC、AB的中点,如果 EF = 3,
D A
那么菱形 ABCD的周长为( )
F
A.24 B.18 E
C.12 D.9 C B
4.若 2x1, x2是一元二次方程 x + x 2 = 0的两个实数根,则 x1 + x2 4x1x2 的值为( )
A.4 B. 3 C.0 D.7
5.对于一次函数 y = 2x + 4,下列说法错误的是( )
A.y随 x的增大而减小 B.图象与 y轴交点为 (0,4)
C.图象经过第一、二、四象限 D.图象经过点 (1,3)
6.六位同学的年龄分别是 13、14、15、14、14、15 岁,关于这组数据,正确说法是( )
A.平均数是 14 B.众数是 14 C.方差是 3 D.中位数是14.5
7.关于 x的一元二次方程 x2 6x + m = 0 有两个不相等的实数根,则 m的值可能是( )
A.8 B.9 C.10 D.11
8.如图,在矩形 ABCD中,对角线 AC,BD相交于点 O,若 OAD = 40 ,
A D
则∠COD的度数为( )
A.20° B.40° O
C.80° D.100° B C
9.随着中考结束,初三某毕业班的每一个同学都向其他同学赠送一张自己的照片留作纪念,全班共送了 2256
张照片,若该班有 x名同学,则根据题意可列出方程为( )
1
A. x(x 1) = 2256 B. x(x +1) = 2256 C. 2x(x 1) = 2256 D. x (x 1) = 2256
2
10.函数 y = ax2 与 y = ax + b 的图象可能是( )
{#{QQABACYCAgwggAAwAgptSBAACAZB5hLCEEwwGGoYCCggiQGsQJEkBiJGcgCkChYRgCGLROBAA4DEIgAINIBAgBINAA=}B#A} A=}#}
y y y y
O x O x O x O x
A. B. C. D.
二、填空题(本题共 6 小题,每题 3 分,共 18 分)
2
11.抛物线 y = 3(x 1) + 5 的顶点坐标为__________.
2
12.已知 A(4, y1 )、 B ( 4, y2 )是抛物线 y = (x + 3) 2 上的两点,则 y1 _______ y2 .
2
.已知 (m 1) xm +113 + 3x 5 = 0 是一元二次方程,则 m的值为__________.
14.为备战东营市第十二届运动会,某县区对甲、乙、丙、丁四名射击运动员进行射击测试,他们射击测
试成绩的平均数 x (单位:环)及方差 s2 如下表所示:
甲 乙 丙 丁
x 9.6 8.9 9.6 9.6
s2 1.4 0.8 2.3 0.8
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择__________.
15.如图所示为一张直角三角形纸片,直角边 AC = 6cm,BC = 8cm,将△ABC折叠,使点 B与点 A重合,
折痕为 DE,则 DE的长为_________cm.
A D
C
D E
B'
A B B C
E F
(第 15 题图) (第 16 题图)
16.如图,正方形 ABCD的边长为 4,E为 AB边的中点,点 F在 BC边上移动,点 B关于直线 EF的对称
点记为 B ,连接 B D , B E , B F .当四边形 BEB F 为正方形时, B D 的长为__________.
三、解答题(共 7 小题,共 52 分)
0 1
17.(6 分)计算: 2 2 + 2 ( 2 1) ( 2019)
16
{#{QQABCAYCAgwggAAwAgptSBAACAZB5hLCEEwwGGoYCCggiQGsQJEkBiJGcgCkChYRgCGLROBAA4DEIgAINIBAgBINAA=}B#A} A=}#}
18.(6 分)解方程
2
(1) (x 2) 9 = 0 (2) x2 + 2x = 3
2
19.(6 分)已知抛物线 y = a (x 1) + h 经过点 (0, 3)和 (3,0).
(1)求 a、h的值;
(2)将该抛物线向上平移 2 个单位长度,再向右平移 1 个单位长度,得到新的抛物线,直接写出新的抛物
线相应的函数表达式.
20.(8 分)如图,在△ABC中, C = 90 ,BD平分∠ABC交 AC于点 D,过 D作 DE∥BC交 AB于点 E,
DF∥AB交 BC于点 F,连接 EF.
(1)求证:四边形 BFDE是菱形;
(2)若 AB = 8, AD = 4 ,求 BF的长.
A
E D
B C
F
{#{QQABCAYCAgwggAAwAgptSBAACAZB5hLCEEwwGGoYCCggiQGsQJEkBiJGcgCkChYRgCGLROBAA4DEIgAINIBAgBINAA=}B#A} A=}#}
21.(8 分)如图,直线 y = 3x + 6 交 x轴和 y轴于点 A和点 B,点C (0, 3)在 y轴上,连接 AC.
(1)求点 A和点 B的坐标;
(2)若点 P是直线 AB上一点,若△BCP的面积为 18,求点 P的坐标.
y
B
A
O x
C
22.(9 分)某县著名传统土特产品“豆笋”“豆干”以“浓郁豆香,绿色健康”享誉全国,深受广大消费者
喜爱.已知 2 件豆笋和 3 件豆干进货价为 240 元,3 件豆笋和 4 件豆干进货价为 340 元.
(1)分别求出每件豆笋、豆干的进价.
3
(2)某特产店计划用不超过 10440 元购进豆笋、豆干共 200 件,且豆笋的数量不低于豆干数量的 ,该特
2
产店有哪几种进货方案?
(3)若该特产店每件豆笋售价为 80 元,每件豆干售价为 55 元,在(2)的条件下,怎样进货可使该特产
店获得利润最大,最大利润为多少元?
{#{QQABACYCAgwggAAwAgptSBAACAZB5hLCEEwwGGoYCCggiQGsQJEkBiJGcgCkChYRgCGLROBAA4DEIgAINIBAgBINAA=}B#A} A=}#}
23.(9 分)定义:对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点
四边形”,如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”
【概念理解】
(1)在已经学过的“①平行四边形;②矩形;③菱形;④正方形”中,_________是“中方四边形”(填序
号).
【性质探究】
(2)如图 1,若四边形 ABCD是“中方四边形”,观察图形,线段 AC和线段 BD有什么关系,并证明你的
结论.
【问题解决】
(3)如图 2,以锐角△ABC的两边 AB,AC为边长,分别向外侧作正方形 ABDE和正方形 ACFG连结 BE,
EG,GC,依次连接四边形 BCGE的四边中点得到四边形 MNRL.求证:四边形 BCGE是“中方四边形”.
A
G
H
E
F
E A
B D
F G D
C B C
图 1 图 2
{#{QQABACYCAgwggAAwAgptSBAACAZB5hLCEEwwGGoYCCggiQGsQJEkBiJGcgCkChYRgCGLROBAA4DEIgAINIBAgBINAA=}B#A} A=}#}
同课章节目录
