北师大版二年级上册数学巧用乘法数图形(二)课件(共17张PPT)
文档属性
| 名称 | 北师大版二年级上册数学巧用乘法数图形(二)课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-17 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
巧用乘法数图形(二)
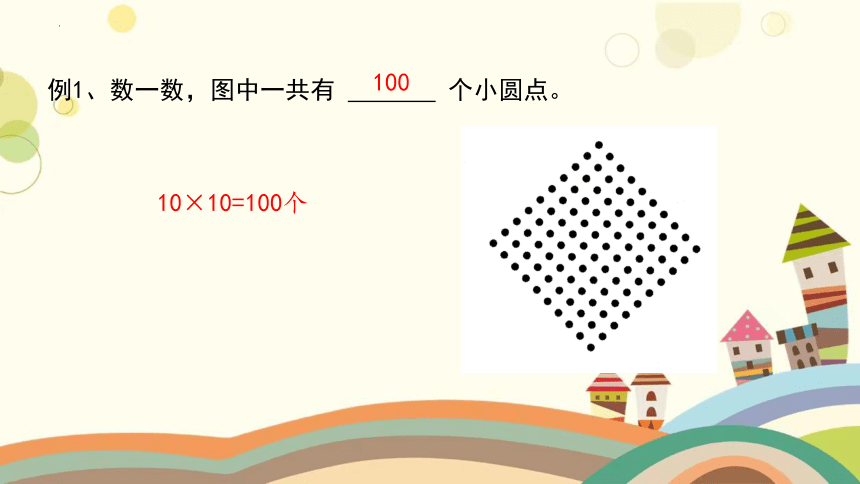
例1、数一数,图中一共有 个小圆点。
10×10=100个
100
例2、右图由多少个点组成?
10×10-4×4=84(个)
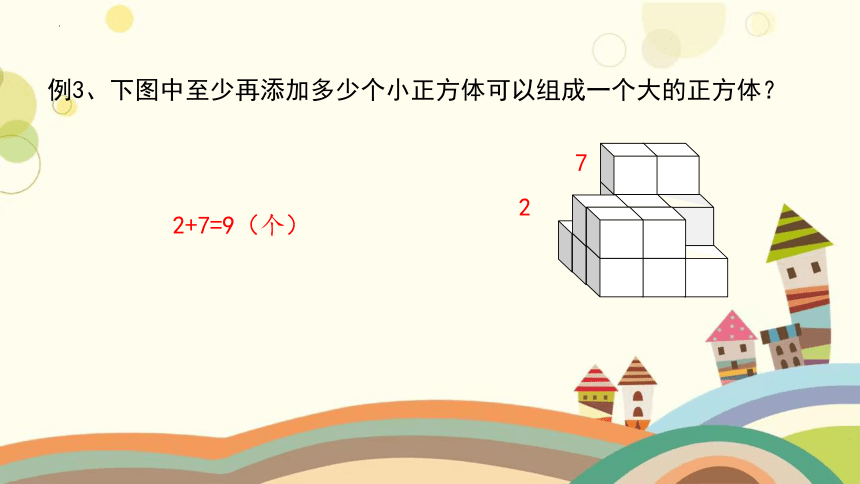
例3、下图中至少再添加多少个小正方体可以组成一个大的正方体?
2
7
2+7=9(个)
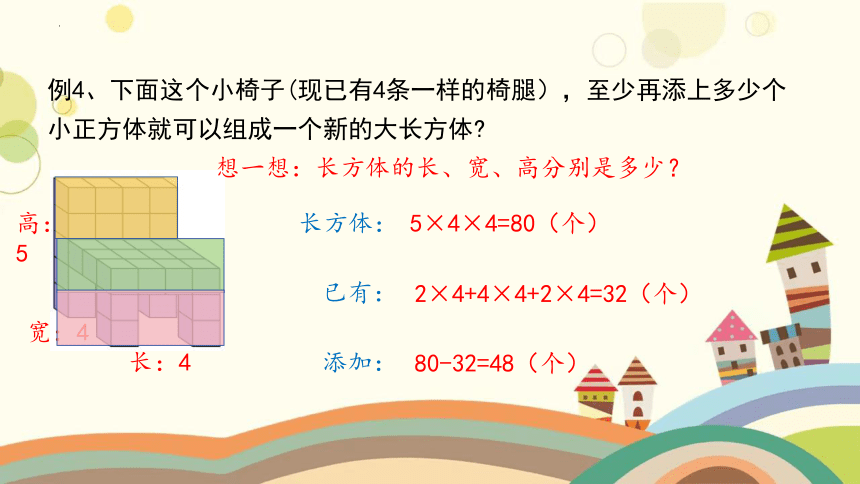
例4、下面这个小椅子(现已有4条一样的椅腿),至少再添上多少个小正方体就可以组成一个新的大长方体
想一想:长方体的长、宽、高分别是多少?
长:4
高:5
宽:4
长方体:
已有:
5×4×4=80(个)
2×4+4×4+2×4=32(个)
80-32=48(个)
添加:
例5、数一数,①号图形的小木块比②号图形的小木块 (填“多”或“少”);多(或少) 块。
大家都来数一数,各有多少块?
①:
2×2×2+1=9(个)
②:
2×2×2+2=10(个)
少
1
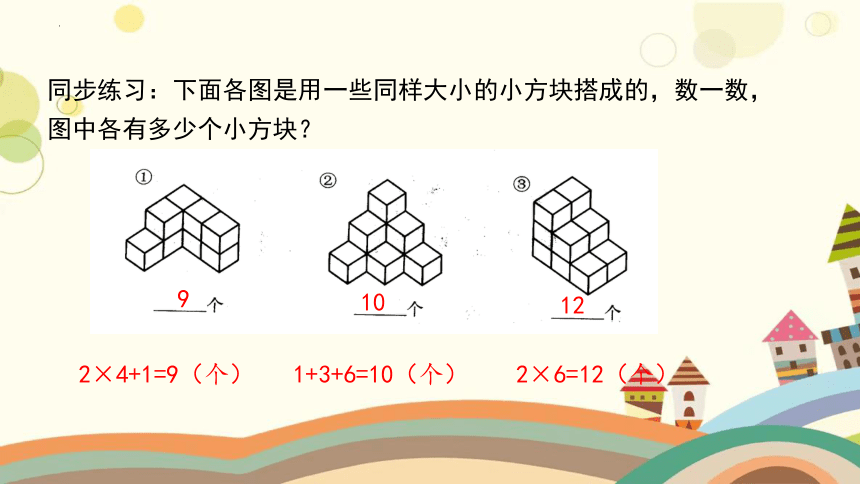
同步练习:下面各图是用一些同样大小的小方块搭成的,数一数,图中各有多少个小方块?
2×4+1=9(个)
1+3+6=10(个)
2×6=12(个)
9
10
12
30~60之间的正方形数:
例6、二年级(一)班的同学人数是一个三角形数,又是一个正方形数,那么该班有多少人?(人数在30~60之间)
6×6=36
7×7=49
1+2+3+4+5+6+7+8=36
答:该班有36人
三角形数:从1开始的连续正整数相加。
正方形数:从1开始的连续奇数之和。
例7、图中有多少个长方形?
横:1+2=3(个)
竖:1+2=3(个)
共:3×3=9(个)
例8、数一数,图中这个宝塔由 个小正方体组成。
第一层:
1个
1
第二层:
1+2=3个
第三层:
第四层:
第五层:
3+3=6个
6+4=10个
10+5=15个
3
6
10
15
1+3+6+10+15=35个
35
例9、有若干根长度相等的火柴棒,把这些火柴摆成下面的图形,照这样摆下去,第10个图中一共用了多少火柴棒?
第一幅:
1个三角形
1×3=3(根)
第二幅:
3个三角形
3×3=9(根)
第三幅:
6个三角形
6×3=18(根)
每三根火柴组成一个三角形,重复的不算!
例9、有若干根长度相等的火柴棒,把这些火柴摆成下面的图形,照这样摆下去,第10个图中一共用了多少火柴棒?
第一幅:
一个三角形
1×3=3(根)
第二幅:
1+2=3个
三角形
3×3=9(根)
第三幅:
1+2+3=6个三角形
6×3=18(根)
第十幅:
1+2+3+4+5+6+7+8+9+10=55(个)
55×3=165(根)
每增加一层,三角形增加的个数就是层数
例10、图A是一个由125个小正方体组成的大正方体。从这个大正方体中抽出一些小正方体,抽的方法是:从一个面到其对面所涉及到的小正方体都要抽掉,图B中黑色阴影部分就是要抽出的部分。则图B中共抽出了 个小正方体。
27
从正面看,被抽出的小正方体:
5×5=25(个)
从右边看,被抽出的小正方体:
1×5=5(个)
重复减去的:3个
25+5-3=27(个)
例11、图A是一个由125个小正方体组成的大正方体。从这个大正方体中抽出一些小正方体,抽的方法是:从一个面到其对面所涉及到的小正方体都要抽掉,图B中黑色阴影部分就是要抽出的部分。则图B中共抽出了 个小正方体。
35
从正面看,被抽出的小正方体:
5×5=25(个)
从右边看,被抽出的小正方体:
3×5=15(个)
重复减去的:
25+15-5=35(个)
1+3+1=5(个)
巧用乘法数图形(二)
例1、数一数,图中一共有 个小圆点。
10×10=100个
100
例2、右图由多少个点组成?
10×10-4×4=84(个)
例3、下图中至少再添加多少个小正方体可以组成一个大的正方体?
2
7
2+7=9(个)
例4、下面这个小椅子(现已有4条一样的椅腿),至少再添上多少个小正方体就可以组成一个新的大长方体
想一想:长方体的长、宽、高分别是多少?
长:4
高:5
宽:4
长方体:
已有:
5×4×4=80(个)
2×4+4×4+2×4=32(个)
80-32=48(个)
添加:
例5、数一数,①号图形的小木块比②号图形的小木块 (填“多”或“少”);多(或少) 块。
大家都来数一数,各有多少块?
①:
2×2×2+1=9(个)
②:
2×2×2+2=10(个)
少
1
同步练习:下面各图是用一些同样大小的小方块搭成的,数一数,图中各有多少个小方块?
2×4+1=9(个)
1+3+6=10(个)
2×6=12(个)
9
10
12
30~60之间的正方形数:
例6、二年级(一)班的同学人数是一个三角形数,又是一个正方形数,那么该班有多少人?(人数在30~60之间)
6×6=36
7×7=49
1+2+3+4+5+6+7+8=36
答:该班有36人
三角形数:从1开始的连续正整数相加。
正方形数:从1开始的连续奇数之和。
例7、图中有多少个长方形?
横:1+2=3(个)
竖:1+2=3(个)
共:3×3=9(个)
例8、数一数,图中这个宝塔由 个小正方体组成。
第一层:
1个
1
第二层:
1+2=3个
第三层:
第四层:
第五层:
3+3=6个
6+4=10个
10+5=15个
3
6
10
15
1+3+6+10+15=35个
35
例9、有若干根长度相等的火柴棒,把这些火柴摆成下面的图形,照这样摆下去,第10个图中一共用了多少火柴棒?
第一幅:
1个三角形
1×3=3(根)
第二幅:
3个三角形
3×3=9(根)
第三幅:
6个三角形
6×3=18(根)
每三根火柴组成一个三角形,重复的不算!
例9、有若干根长度相等的火柴棒,把这些火柴摆成下面的图形,照这样摆下去,第10个图中一共用了多少火柴棒?
第一幅:
一个三角形
1×3=3(根)
第二幅:
1+2=3个
三角形
3×3=9(根)
第三幅:
1+2+3=6个三角形
6×3=18(根)
第十幅:
1+2+3+4+5+6+7+8+9+10=55(个)
55×3=165(根)
每增加一层,三角形增加的个数就是层数
例10、图A是一个由125个小正方体组成的大正方体。从这个大正方体中抽出一些小正方体,抽的方法是:从一个面到其对面所涉及到的小正方体都要抽掉,图B中黑色阴影部分就是要抽出的部分。则图B中共抽出了 个小正方体。
27
从正面看,被抽出的小正方体:
5×5=25(个)
从右边看,被抽出的小正方体:
1×5=5(个)
重复减去的:3个
25+5-3=27(个)
例11、图A是一个由125个小正方体组成的大正方体。从这个大正方体中抽出一些小正方体,抽的方法是:从一个面到其对面所涉及到的小正方体都要抽掉,图B中黑色阴影部分就是要抽出的部分。则图B中共抽出了 个小正方体。
35
从正面看,被抽出的小正方体:
5×5=25(个)
从右边看,被抽出的小正方体:
3×5=15(个)
重复减去的:
25+15-5=35(个)
1+3+1=5(个)
