2024-2025学年江西省宜春市丰城九中九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年江西省宜春市丰城九中九年级(上)开学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 116.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-17 00:00:00 | ||
图片预览




文档简介
2024-2025学年江西省宜春市丰城九中九年级(上)开学数学试卷
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.数学是一门美丽的学科,在平面直角坐标系内可以利用函数画出许多漂亮的曲线,下列曲线中,既是中心对称图形,也是轴对称图形的是( )
A. 三叶玫瑰线 B. 四叶玫瑰线
C. 心形线 D. 笛卡尔叶形线
2.小冰和小雪自愿参加学校组织的课后托管服务活动,随机选择自主阅读、体育活动、科普活动三项中的某一项,那么小冰和小雪同时选择“体育活动”的概率为( )
A. B. C. D.
3.如图,绕点按顺时针方向旋转后与重合,连接,则( )
A.
B.
C.
D.
4.如图,为的直径,点,在上若,则的度数是( )
A.
B.
C.
D.
5.关于的方程有实数根,则的取值范围是( )
A. B. C. 且 D. 且
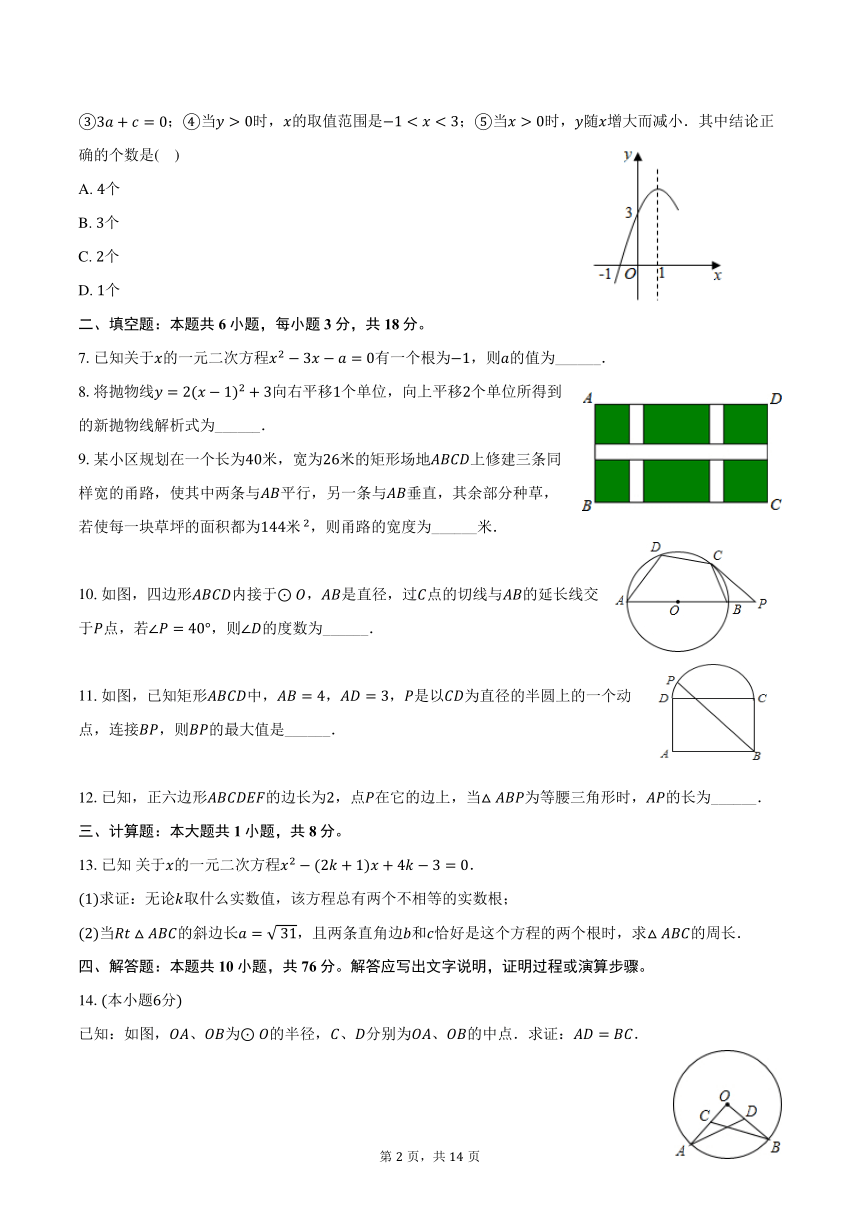
6.如图,抛物线的对称轴为直线,与轴的一个交点坐标为,其部分图象如图所示,下列结论:;方程的两个根是,;;当时,的取值范围是;当时,随增大而减小.其中结论正确的个数是( )
A. 个
B. 个
C. 个
D. 个
二、填空题:本题共6小题,每小题3分,共18分。
7.已知关于的一元二次方程有一个根为,则的值为______.
8.将抛物线向右平移个单位,向上平移个单位所得到的新抛物线解析式为______.
9.某小区规划在一个长为米,宽为米的矩形场地上修建三条同样宽的甬路,使其中两条与平行,另一条与垂直,其余部分种草,若使每一块草坪的面积都为米,则甬路的宽度为______米.
10.如图,四边形内接于,是直径,过点的切线与的延长线交于点,若,则的度数为______.
11.如图,已知矩形中,,,是以为直径的半圆上的一个动点,连接,则的最大值是______.
12.已知,正六边形的边长为,点在它的边上,当为等腰三角形时,的长为______.
三、计算题:本大题共1小题,共8分。
13.已知 关于的一元二次方程.
求证:无论取什么实数值,该方程总有两个不相等的实数根;
当的斜边长,且两条直角边和恰好是这个方程的两个根时,求的周长.
四、解答题:本题共10小题,共76分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
已知:如图,、为的半径,、分别为、的中点.求证:.
15.本小题分
先化简,再求值:,其中是一元二次方程的根.
16.本小题分
如图,在网格中每个小正方形的边长都是,线段的两个端点都在格点上,,,将线段绕点顺时针旋转,得到线段.
旋转过程中点运动的路径长为______;
在网格中用无刻度直尺作图:不写作法,保留作图痕迹
画出线段,则点的坐标为______;
作出的外心.
17.本小题分
一个不透明的口袋中装有个红球和个白球,它们除颜色外完全相同.
判断事件“从口袋中随机摸出一个球是蓝球”是什么事件,并写出其发生的概率;
现从口袋中取走若干个白球,并放入相同数量的红球,充分摇匀后,若从口袋中随机摸出一个球是白球的概率是,则取走了多少个白球?
18.本小题分
如图,在中,,以点为圆心,长为半径作圆,交于点,交于点,连接.
若,求的度数;
若,,求的长.
19.本小题分
由于新冠疫情的影响,口罩需求量急剧上升,经过连续两次价格的上调,口罩的价格由每包元涨到了每包元.
求出这两次价格上调的平均增长率;
在有关部门大力调控下,口罩价格还是降到了每包元,而且调查发现,定价为每包元时,一天可以卖出包,每降价元,可以多卖出包.当销售额为元时,为让顾客获得更大的优惠,应该降价多少元?
20.本小题分
如图,点是正方形的边延长线上一点,且,连接交于点,以点为圆心,为半径作,交线段于点.
求证:是的切线;
若,求阴影部分的面积.
21.本小题分
九年级数学兴趣小组在课外学习时遇到这样一个问题:
定义:如果二次函数是常数与是常数满足,,,则这两个函数互为“旋转函数”求函数的“旋转函数”.
小组同学是这样思考的,由函数可知,,,,根据,,,求出,,就能确定这个函数的“旋转函数”.
请参照小组同学的方法解决下面问题:
函数的“旋转函数”是______;
若函数与互为“旋转函数”,求的值;
已知函数的图象与轴交于,两点,与轴交于点,点,,关于原点的对称点分别是,,,试求证:经过点,,的二次函数与互为“旋转函数”.
22.本小题分
九年级一班同学在数学老师的指导下,以“等腰三角形的旋转”为主题,开展数学探究活动.
操作探究:
如图,为等腰三角形,,,将绕点旋转,得到,连接,是的中点,连接,则 ______,与的数量关系是______;
迁移探究:
如图,中的其他条件不变,当绕点逆时针旋转,点正好落在的角平分线上,得到,求出此时的度数及与的数量关系;
拓展应用:
如图,在等腰三角形中,,将绕点旋转,得到,连接,是的中点,连接当时,请直接写出的长.
23.本小题分
已知抛物线顶点在第三象限,顶点纵坐标为.
求抛物线的函数表达式和顶点坐标;
若图象与轴的交点为、,与轴的交点,求的面积;
在对称轴上找一点,使的值最小,求满足条件的点坐标;
在抛物线上是否存在一点,使得是以为直角边的直角三角形?存在,求出点坐标;不存在,说出理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或或
13.解:关于的一元二次方程,
恒成立,
故无论取什么实数值,该方程总有两个不相等的实数根;
根据勾股定理得:
因为两条直角边和恰好是这个方程的两个根,
则,,
因为,
即,
整理得:,即,
解得:,,
即即,
舍去,
则,
又因为,
则的周长.
14.证明:,为的半径,,分别为,的中点,
,.
在与中,
,
≌.
.
15.解:
,
是一元二次方程的根,
,
则原式.
16.;
如图所示,线段即为所求:
,,
;
如图点即为所求:
是直角三角形,即,
的外心即为的中点,
如图中所示,点即为所求
17.解:因为口袋中装有个红球和个白球,
所以“从口袋中随机摸出一个球是蓝球”是不可能事件,
所以它发生的概率是.
设取走了个白球.
由题意,得,
解得.
故取走了个白球.
18.解:如图,连接.
,,
.
,
,
,
.
又,
.
如图,过点作,垂足为.
,,,
.
又,
,
.
,,
.
19.解:设这两次价格上调的平均增长率为,
依题意得:,
解得:,不符合题意,舍去.
答:这两次价格上调的平均增长率为;
设每包应该降价元,则每包的售价为元,每天可售出包,
依题意得:,
整理得:,
解得:,.
又要让顾客获得更大的优惠,
的值为.
答:每包应该降价元.
20.证明:过作于,
四边形是正方形,
,,
,
,
,
,
,
是的切线;
解:四边形是正方形,
,
是等腰直角三角形,
,
,
,
,
,
,
阴影部分的面积的面积扇形的面积.
21.
【解析】解:由函数知,,,,
,,,
,,,
,
故答案为:;
解:根据题意得:,解得,
;
证明:化简得,
则、、三点的坐标分别为,,,
、、三点关于原点对称的点坐标分别为,,,
经过、、三点的函数解析式为,
与原函数是旋转函数.
22.解:;.
由旋转的性质,可知≌,
为等边三角形,平分,为等边三角形,
,,
,
,
,
是等腰直角三角形,,
是的中点,
,
是等腰直角三角形,
.
或.
23.解:,
又抛物线顶点纵坐标为,
,
解得:或此时顶点不在第三象限,舍去,
抛物线的函数表达式:,
,
顶点坐标为;
令;
解得:或,
点,,
,
将代入得:,
点,即,
,
的面积为;
如图:
点关于对称轴对称的点为点,
,
,
,,共线时,最小,即线段与对称轴的交点即为点,
由,可得直线解析式为,
在中,令得,
点坐标;
在抛物线上存在一点,使得是以为直角边的直角三角形,理由如下:
以点为直角顶点的直角三角形,过作轴于,如图:
,
,
,
,
是等腰直角三角形,
设,则,
,
,
点在抛物线上,
,
解得,,,不合题意,舍去,
点;
以为直角顶点,设抛物线顶点,连接,过作轴于,如图:
由知,
,
,,,
,
,
,
点即是点,
点,
综上所述,满足条件的点坐标为或.
第1页,共1页
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.数学是一门美丽的学科,在平面直角坐标系内可以利用函数画出许多漂亮的曲线,下列曲线中,既是中心对称图形,也是轴对称图形的是( )
A. 三叶玫瑰线 B. 四叶玫瑰线
C. 心形线 D. 笛卡尔叶形线
2.小冰和小雪自愿参加学校组织的课后托管服务活动,随机选择自主阅读、体育活动、科普活动三项中的某一项,那么小冰和小雪同时选择“体育活动”的概率为( )
A. B. C. D.
3.如图,绕点按顺时针方向旋转后与重合,连接,则( )
A.
B.
C.
D.
4.如图,为的直径,点,在上若,则的度数是( )
A.
B.
C.
D.
5.关于的方程有实数根,则的取值范围是( )
A. B. C. 且 D. 且
6.如图,抛物线的对称轴为直线,与轴的一个交点坐标为,其部分图象如图所示,下列结论:;方程的两个根是,;;当时,的取值范围是;当时,随增大而减小.其中结论正确的个数是( )
A. 个
B. 个
C. 个
D. 个
二、填空题:本题共6小题,每小题3分,共18分。
7.已知关于的一元二次方程有一个根为,则的值为______.
8.将抛物线向右平移个单位,向上平移个单位所得到的新抛物线解析式为______.
9.某小区规划在一个长为米,宽为米的矩形场地上修建三条同样宽的甬路,使其中两条与平行,另一条与垂直,其余部分种草,若使每一块草坪的面积都为米,则甬路的宽度为______米.
10.如图,四边形内接于,是直径,过点的切线与的延长线交于点,若,则的度数为______.
11.如图,已知矩形中,,,是以为直径的半圆上的一个动点,连接,则的最大值是______.
12.已知,正六边形的边长为,点在它的边上,当为等腰三角形时,的长为______.
三、计算题:本大题共1小题,共8分。
13.已知 关于的一元二次方程.
求证:无论取什么实数值,该方程总有两个不相等的实数根;
当的斜边长,且两条直角边和恰好是这个方程的两个根时,求的周长.
四、解答题:本题共10小题,共76分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
已知:如图,、为的半径,、分别为、的中点.求证:.
15.本小题分
先化简,再求值:,其中是一元二次方程的根.
16.本小题分
如图,在网格中每个小正方形的边长都是,线段的两个端点都在格点上,,,将线段绕点顺时针旋转,得到线段.
旋转过程中点运动的路径长为______;
在网格中用无刻度直尺作图:不写作法,保留作图痕迹
画出线段,则点的坐标为______;
作出的外心.
17.本小题分
一个不透明的口袋中装有个红球和个白球,它们除颜色外完全相同.
判断事件“从口袋中随机摸出一个球是蓝球”是什么事件,并写出其发生的概率;
现从口袋中取走若干个白球,并放入相同数量的红球,充分摇匀后,若从口袋中随机摸出一个球是白球的概率是,则取走了多少个白球?
18.本小题分
如图,在中,,以点为圆心,长为半径作圆,交于点,交于点,连接.
若,求的度数;
若,,求的长.
19.本小题分
由于新冠疫情的影响,口罩需求量急剧上升,经过连续两次价格的上调,口罩的价格由每包元涨到了每包元.
求出这两次价格上调的平均增长率;
在有关部门大力调控下,口罩价格还是降到了每包元,而且调查发现,定价为每包元时,一天可以卖出包,每降价元,可以多卖出包.当销售额为元时,为让顾客获得更大的优惠,应该降价多少元?
20.本小题分
如图,点是正方形的边延长线上一点,且,连接交于点,以点为圆心,为半径作,交线段于点.
求证:是的切线;
若,求阴影部分的面积.
21.本小题分
九年级数学兴趣小组在课外学习时遇到这样一个问题:
定义:如果二次函数是常数与是常数满足,,,则这两个函数互为“旋转函数”求函数的“旋转函数”.
小组同学是这样思考的,由函数可知,,,,根据,,,求出,,就能确定这个函数的“旋转函数”.
请参照小组同学的方法解决下面问题:
函数的“旋转函数”是______;
若函数与互为“旋转函数”,求的值;
已知函数的图象与轴交于,两点,与轴交于点,点,,关于原点的对称点分别是,,,试求证:经过点,,的二次函数与互为“旋转函数”.
22.本小题分
九年级一班同学在数学老师的指导下,以“等腰三角形的旋转”为主题,开展数学探究活动.
操作探究:
如图,为等腰三角形,,,将绕点旋转,得到,连接,是的中点,连接,则 ______,与的数量关系是______;
迁移探究:
如图,中的其他条件不变,当绕点逆时针旋转,点正好落在的角平分线上,得到,求出此时的度数及与的数量关系;
拓展应用:
如图,在等腰三角形中,,将绕点旋转,得到,连接,是的中点,连接当时,请直接写出的长.
23.本小题分
已知抛物线顶点在第三象限,顶点纵坐标为.
求抛物线的函数表达式和顶点坐标;
若图象与轴的交点为、,与轴的交点,求的面积;
在对称轴上找一点,使的值最小,求满足条件的点坐标;
在抛物线上是否存在一点,使得是以为直角边的直角三角形?存在,求出点坐标;不存在,说出理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或或
13.解:关于的一元二次方程,
恒成立,
故无论取什么实数值,该方程总有两个不相等的实数根;
根据勾股定理得:
因为两条直角边和恰好是这个方程的两个根,
则,,
因为,
即,
整理得:,即,
解得:,,
即即,
舍去,
则,
又因为,
则的周长.
14.证明:,为的半径,,分别为,的中点,
,.
在与中,
,
≌.
.
15.解:
,
是一元二次方程的根,
,
则原式.
16.;
如图所示,线段即为所求:
,,
;
如图点即为所求:
是直角三角形,即,
的外心即为的中点,
如图中所示,点即为所求
17.解:因为口袋中装有个红球和个白球,
所以“从口袋中随机摸出一个球是蓝球”是不可能事件,
所以它发生的概率是.
设取走了个白球.
由题意,得,
解得.
故取走了个白球.
18.解:如图,连接.
,,
.
,
,
,
.
又,
.
如图,过点作,垂足为.
,,,
.
又,
,
.
,,
.
19.解:设这两次价格上调的平均增长率为,
依题意得:,
解得:,不符合题意,舍去.
答:这两次价格上调的平均增长率为;
设每包应该降价元,则每包的售价为元,每天可售出包,
依题意得:,
整理得:,
解得:,.
又要让顾客获得更大的优惠,
的值为.
答:每包应该降价元.
20.证明:过作于,
四边形是正方形,
,,
,
,
,
,
,
是的切线;
解:四边形是正方形,
,
是等腰直角三角形,
,
,
,
,
,
,
阴影部分的面积的面积扇形的面积.
21.
【解析】解:由函数知,,,,
,,,
,,,
,
故答案为:;
解:根据题意得:,解得,
;
证明:化简得,
则、、三点的坐标分别为,,,
、、三点关于原点对称的点坐标分别为,,,
经过、、三点的函数解析式为,
与原函数是旋转函数.
22.解:;.
由旋转的性质,可知≌,
为等边三角形,平分,为等边三角形,
,,
,
,
,
是等腰直角三角形,,
是的中点,
,
是等腰直角三角形,
.
或.
23.解:,
又抛物线顶点纵坐标为,
,
解得:或此时顶点不在第三象限,舍去,
抛物线的函数表达式:,
,
顶点坐标为;
令;
解得:或,
点,,
,
将代入得:,
点,即,
,
的面积为;
如图:
点关于对称轴对称的点为点,
,
,
,,共线时,最小,即线段与对称轴的交点即为点,
由,可得直线解析式为,
在中,令得,
点坐标;
在抛物线上存在一点,使得是以为直角边的直角三角形,理由如下:
以点为直角顶点的直角三角形,过作轴于,如图:
,
,
,
,
是等腰直角三角形,
设,则,
,
,
点在抛物线上,
,
解得,,,不合题意,舍去,
点;
以为直角顶点,设抛物线顶点,连接,过作轴于,如图:
由知,
,
,,,
,
,
,
点即是点,
点,
综上所述,满足条件的点坐标为或.
第1页,共1页
同课章节目录
