2024-2025学年黑龙江省哈尔滨市双城区兆麟中学九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年黑龙江省哈尔滨市双城区兆麟中学九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 191.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-17 08:31:17 | ||
图片预览



文档简介
2024-2025学年黑龙江省哈尔滨市双城区兆麟中学九年级(上)开学
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程是关于的一元二次方程的是( )
A. B. C. D.
2.下列四边形中不是轴对称图形的是( )
A. 矩形 B. 菱形 C. 正方形 D. 平行四边形
3.如图所示的图象分别给出了与的对应关系,其中表示是的函数的是( )
A. B. C. D.
4.下列各组数中,能作为一个直角三角形的三边长的是( )
A. ,, B. ,, C. ,, D. ,,
5.关于正比例函数下列说法正确的是( )
A. 图象不经过原点 B. 随的增大而增大
C. 图象经过第二、四象限 D. 当时,
6.若关于的一元二次方程有实数根,则的取值范围为( )
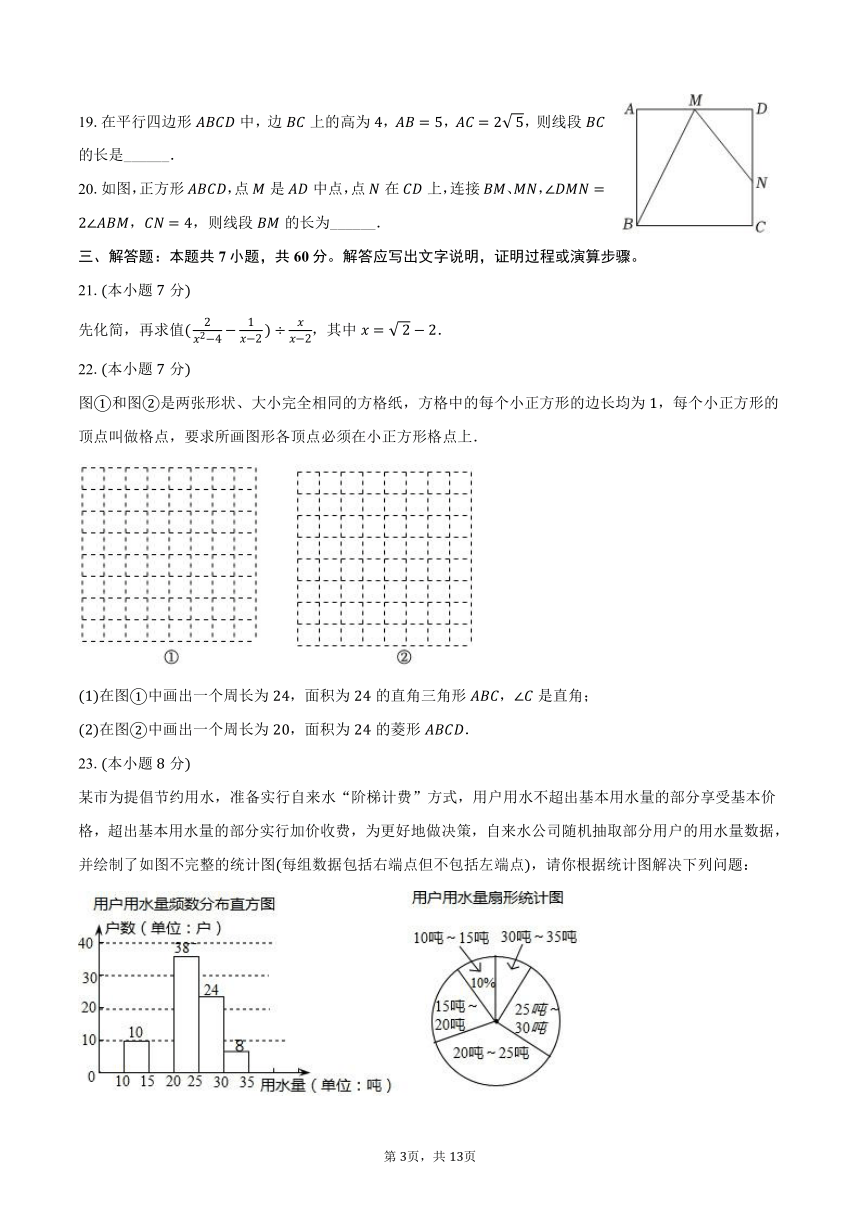
A. B. C. D.
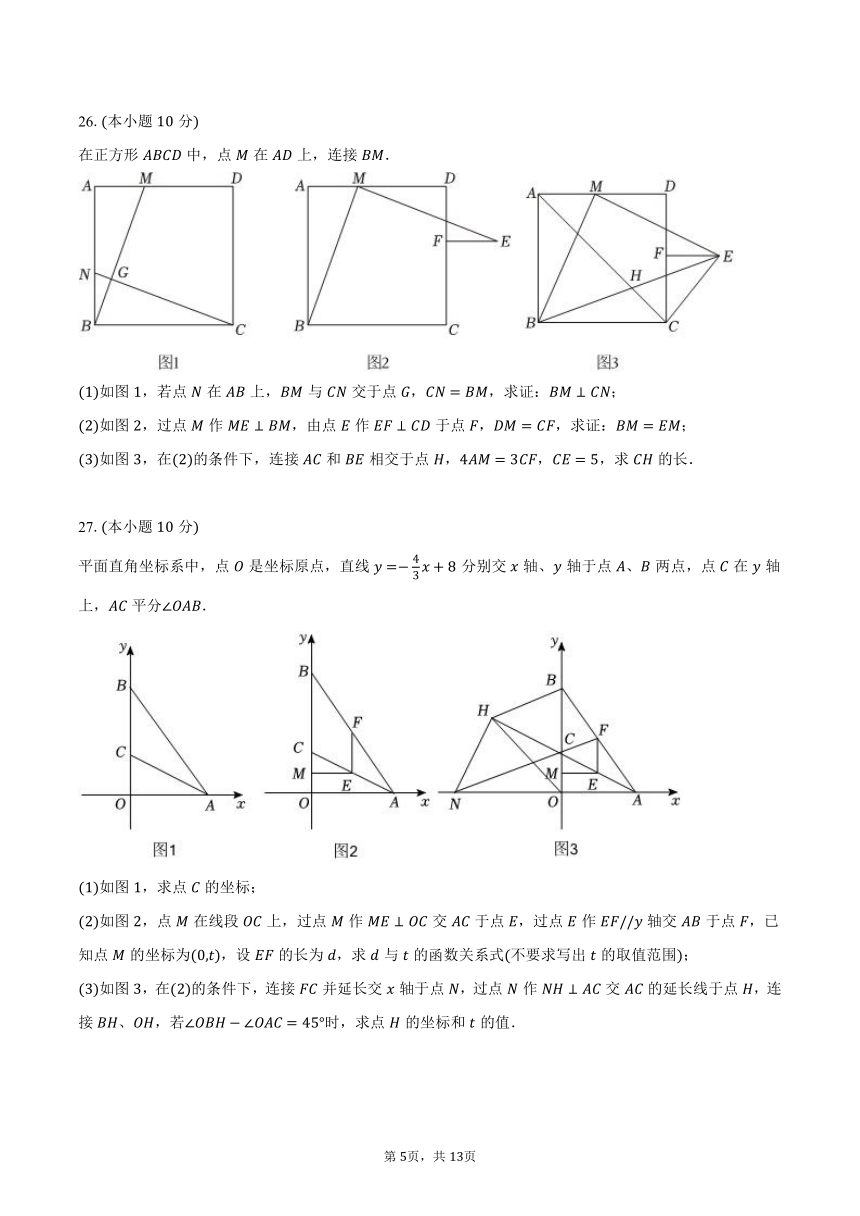
7.如图,在四边形中,对角线,相交于点,,添加下列条件,不能判定四边形是菱形的是( )
A. B.
C. D.
8.如图,矩形的长,宽,将它折叠,使点与点重合,求折叠后的长和的长分别是( )
A. ,
B. ,
C. ,
D. ,
9.直线向下平移个单位长度后,经过点,则的值是( )
A. B. C. D.
10.甲、乙两车从城出发前往城,在整个过程中,汽车离开城的距离与时间的对应关系如图所示,下列说法:
、两城相距
甲车比乙车多用两个小时
甲车出发一个半小时后被乙车追上
甲乙两车的速度比为:
乙车追上甲车时距终点城还有
其中正确的说法是( )
A. B. C. D.
二、填空题:本题共10小题,每小题3分,共30分。
11.在函数中,自变量的取值范围是 .
12.计算的结果是______.
13.解一元二次方程的根是______.
14.若一组数据,,,,,的平均数是,则这组数据的众数是______.
15.如图,在中,,,点,,分别是,,的中点,
则四边形的周长为______.
16.如图所示,已知函数与函数的图象交于点,则不等式的解集是______.
17.如图,菱形的对角线与相交于点,为边的中点,连接若,,则 ______.
18.已知一次函数的图象经过第一、三、四象限,则的取值范围是______.
19.在平行四边形中,边上的高为,,,则线段的长是______.
20.如图,正方形,点是中点,点在上,连接、,,,则线段的长为______.
三、解答题:本题共7小题,共60分。解答应写出文字说明,证明过程或演算步骤。
21.本小题分
先化简,再求值,其中.
22.本小题分
图和图是两张形状、大小完全相同的方格纸,方格中的每个小正方形的边长均为,每个小正方形的顶点叫做格点,要求所画图形各顶点必须在小正方形格点上.
在图中画出一个周长为,面积为的直角三角形,是直角;
在图中画出一个周长为,面积为的菱形.
23.本小题分
某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图每组数据包括右端点但不包括左端点,请你根据统计图解决下列问题:
此次抽样调查的样本容量是______.
补全频数分布直方图.
如果自来水公司将基本用水量定为每户吨,那么该地区万用户中约有多少用户的用水全部享受基本价格?
24.本小题分
已知在中,,点、分别为、的中点,点在的延长线上,连接、、,且.
如图,求证:四边形是平行四边形;
如图,连接、,在不添加任何辅助线和字母的前提下,请直接写出图中与面积相等的四个三角形除外.
25.本小题分
年哈尔滨马拉松比赛期间,某体育用品商店迎合市场热度,计划购进、种两种品牌的跑步鞋,若购进双品牌跑步鞋和双品牌跑步鞋,需要元,若购进双品牌跑步鞋和双品牌跑步鞋,需要元.
求该商店购进、两种品牌跑步鞋的单价分别是多少元?
若商店共购进两种跑步鞋双,且品牌跑鞋的数量不多于品牌跑步鞋的,如果这两种跑步鞋每双均加价出售,当购进品牌跑步鞋多少双时,商店获得的总利润最大,总利润最大是多少?
26.本小题分
在正方形中,点在上,连接.
如图,若点在上,与交于点,,求证:;
如图,过点作,由点作于点,,求证:;
如图,在的条件下,连接和相交于点,,,求的长.
27.本小题分
平面直角坐标系中,点是坐标原点,直线分别交轴、轴于点、两点,点在轴上,平分.
如图,求点的坐标;
如图,点在线段上,过点作交于点,过点作轴交于点,已知点的坐标为,设的长为,求与的函数关系式不要求写出的取值范围;
如图,在的条件下,连接并延长交轴于点,过点作交的延长线于点,连接、,若时,求点的坐标和的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.且
12.
13.,
14.
15.
16.
17.
18.
19.或
20.
21.解:
,
当时,原式.
22.解:如图,直角三角形即为所求.
如图,菱形即为所求.
23.
“吨吨”部分的户数为户,
补全图形如下:
万户,
答:该地区万用户中约有万用户的用水全部享受基本价格.
24.证明:点、分别是、的中点,
是的中位线,
,
,,
,
,
,
,
四边形是平行四边形.
如图中,与面积相等的三角形有:,,,.
理由:四边形是平行四边形,
与的面积相等,
,,
与,与的面积相等,
与面积相等的三角形有:,,,.
25.解:设每个品牌跑步鞋的单价元、每个品牌跑步鞋的单价元,
根据题意,得:,
解得:,
答:每个品牌跑步鞋的单价为元、每个品牌跑步鞋的单价为元;
两种跑步鞋双,且品牌跑鞋的数量不多于品牌跑步鞋的,
,
解得:,
,
解得:,
,
在,
,
随的增大而增大,
当时,取得最大值,最大值为,
即最大利润为元.
应购进品牌跑步鞋个,销售利润最大,为元.
26.证明:正方形,
,,
,
≌,
,
,
,
;
证明:过作于,而,
,
,
,
,,
,
,
,
四边形是矩形,
,
≌,
;
解:如图,过作于,延长交于,则,四边形为矩形,四边形为矩形,
,,
设,而,
,,
,
≌,
,
,
,
,
解得:,舍去,
,,,
正方形,
,
设,
,
,
,
解得:,经检验符合题意;
,
.
27.解:如图,过作于,
,平分,
,
,
直线分别交轴、轴于点、两点,当,则;当,则;
,,
,
,
,,
;
解:,,设直线为,
,
解得,
直线为;
,点的坐标为,,
解得:,
,
在上,直线为,轴,
,
,
;
解:如图,延长交轴于,则,
,
,
,
,
,
,
,
平分,
,
,
,
≌,
,
,
,
,
,即,
,
,
设直线为,
,
解得:,
直线为,
联立得,
解得:,
,
,,
同理可得:直线为,
联立得,
解得:,
即,
,
,
解得,经检验符合题意.
第1页,共1页
数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程是关于的一元二次方程的是( )
A. B. C. D.
2.下列四边形中不是轴对称图形的是( )
A. 矩形 B. 菱形 C. 正方形 D. 平行四边形
3.如图所示的图象分别给出了与的对应关系,其中表示是的函数的是( )
A. B. C. D.
4.下列各组数中,能作为一个直角三角形的三边长的是( )
A. ,, B. ,, C. ,, D. ,,
5.关于正比例函数下列说法正确的是( )
A. 图象不经过原点 B. 随的增大而增大
C. 图象经过第二、四象限 D. 当时,
6.若关于的一元二次方程有实数根,则的取值范围为( )
A. B. C. D.
7.如图,在四边形中,对角线,相交于点,,添加下列条件,不能判定四边形是菱形的是( )
A. B.
C. D.
8.如图,矩形的长,宽,将它折叠,使点与点重合,求折叠后的长和的长分别是( )
A. ,
B. ,
C. ,
D. ,
9.直线向下平移个单位长度后,经过点,则的值是( )
A. B. C. D.
10.甲、乙两车从城出发前往城,在整个过程中,汽车离开城的距离与时间的对应关系如图所示,下列说法:
、两城相距
甲车比乙车多用两个小时
甲车出发一个半小时后被乙车追上
甲乙两车的速度比为:
乙车追上甲车时距终点城还有
其中正确的说法是( )
A. B. C. D.
二、填空题:本题共10小题,每小题3分,共30分。
11.在函数中,自变量的取值范围是 .
12.计算的结果是______.
13.解一元二次方程的根是______.
14.若一组数据,,,,,的平均数是,则这组数据的众数是______.
15.如图,在中,,,点,,分别是,,的中点,
则四边形的周长为______.
16.如图所示,已知函数与函数的图象交于点,则不等式的解集是______.
17.如图,菱形的对角线与相交于点,为边的中点,连接若,,则 ______.
18.已知一次函数的图象经过第一、三、四象限,则的取值范围是______.
19.在平行四边形中,边上的高为,,,则线段的长是______.
20.如图,正方形,点是中点,点在上,连接、,,,则线段的长为______.
三、解答题:本题共7小题,共60分。解答应写出文字说明,证明过程或演算步骤。
21.本小题分
先化简,再求值,其中.
22.本小题分
图和图是两张形状、大小完全相同的方格纸,方格中的每个小正方形的边长均为,每个小正方形的顶点叫做格点,要求所画图形各顶点必须在小正方形格点上.
在图中画出一个周长为,面积为的直角三角形,是直角;
在图中画出一个周长为,面积为的菱形.
23.本小题分
某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图每组数据包括右端点但不包括左端点,请你根据统计图解决下列问题:
此次抽样调查的样本容量是______.
补全频数分布直方图.
如果自来水公司将基本用水量定为每户吨,那么该地区万用户中约有多少用户的用水全部享受基本价格?
24.本小题分
已知在中,,点、分别为、的中点,点在的延长线上,连接、、,且.
如图,求证:四边形是平行四边形;
如图,连接、,在不添加任何辅助线和字母的前提下,请直接写出图中与面积相等的四个三角形除外.
25.本小题分
年哈尔滨马拉松比赛期间,某体育用品商店迎合市场热度,计划购进、种两种品牌的跑步鞋,若购进双品牌跑步鞋和双品牌跑步鞋,需要元,若购进双品牌跑步鞋和双品牌跑步鞋,需要元.
求该商店购进、两种品牌跑步鞋的单价分别是多少元?
若商店共购进两种跑步鞋双,且品牌跑鞋的数量不多于品牌跑步鞋的,如果这两种跑步鞋每双均加价出售,当购进品牌跑步鞋多少双时,商店获得的总利润最大,总利润最大是多少?
26.本小题分
在正方形中,点在上,连接.
如图,若点在上,与交于点,,求证:;
如图,过点作,由点作于点,,求证:;
如图,在的条件下,连接和相交于点,,,求的长.
27.本小题分
平面直角坐标系中,点是坐标原点,直线分别交轴、轴于点、两点,点在轴上,平分.
如图,求点的坐标;
如图,点在线段上,过点作交于点,过点作轴交于点,已知点的坐标为,设的长为,求与的函数关系式不要求写出的取值范围;
如图,在的条件下,连接并延长交轴于点,过点作交的延长线于点,连接、,若时,求点的坐标和的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.且
12.
13.,
14.
15.
16.
17.
18.
19.或
20.
21.解:
,
当时,原式.
22.解:如图,直角三角形即为所求.
如图,菱形即为所求.
23.
“吨吨”部分的户数为户,
补全图形如下:
万户,
答:该地区万用户中约有万用户的用水全部享受基本价格.
24.证明:点、分别是、的中点,
是的中位线,
,
,,
,
,
,
,
四边形是平行四边形.
如图中,与面积相等的三角形有:,,,.
理由:四边形是平行四边形,
与的面积相等,
,,
与,与的面积相等,
与面积相等的三角形有:,,,.
25.解:设每个品牌跑步鞋的单价元、每个品牌跑步鞋的单价元,
根据题意,得:,
解得:,
答:每个品牌跑步鞋的单价为元、每个品牌跑步鞋的单价为元;
两种跑步鞋双,且品牌跑鞋的数量不多于品牌跑步鞋的,
,
解得:,
,
解得:,
,
在,
,
随的增大而增大,
当时,取得最大值,最大值为,
即最大利润为元.
应购进品牌跑步鞋个,销售利润最大,为元.
26.证明:正方形,
,,
,
≌,
,
,
,
;
证明:过作于,而,
,
,
,
,,
,
,
,
四边形是矩形,
,
≌,
;
解:如图,过作于,延长交于,则,四边形为矩形,四边形为矩形,
,,
设,而,
,,
,
≌,
,
,
,
,
解得:,舍去,
,,,
正方形,
,
设,
,
,
,
解得:,经检验符合题意;
,
.
27.解:如图,过作于,
,平分,
,
,
直线分别交轴、轴于点、两点,当,则;当,则;
,,
,
,
,,
;
解:,,设直线为,
,
解得,
直线为;
,点的坐标为,,
解得:,
,
在上,直线为,轴,
,
,
;
解:如图,延长交轴于,则,
,
,
,
,
,
,
,
平分,
,
,
,
≌,
,
,
,
,
,即,
,
,
设直线为,
,
解得:,
直线为,
联立得,
解得:,
,
,,
同理可得:直线为,
联立得,
解得:,
即,
,
,
解得,经检验符合题意.
第1页,共1页
同课章节目录
