2024-2025学年陕西省西安市灞桥区铁一中滨河学校九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年陕西省西安市灞桥区铁一中滨河学校九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 82.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-17 09:16:17 | ||
图片预览




文档简介
2024-2025学年陕西省西安市灞桥区铁一中滨河学校九年级(上)开学数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程中,属于一元二次方程的是( )
A. B. C. D.
2.已知,则下列比例式正确的是( )
A. B. C. D.
3.如图,,,,,那么的长为( )
A.
B.
C.
D.
4.如图,在矩形中,对角线与相交于点,若,则的度数( )
A.
B.
C.
D.
5.在一个不透明的袋子里有红球、黄球共个,这些球除颜色外都相同,小明通过多次实验发现,摸到红球的频率稳定在左右,则袋子中红球的个数可能是( )
A. B. C. D.
6.龙年春晚主题为“龙行龘龘,欣欣家园”,“龘”这个字引发一波热门关注,据记载,“龘”出自第一部楷书字典玉篇,“龙行龘龘”形容龙腾飞的样子,昂扬而热烈某服装店购进一款印有“鬣”字图案的上衣,据店长统计,该款上衣月份销售量为件,月份销售量为件,则该款上衣销售量的月平均增长率为( )
A. B. C. D.
7.若实数,满足,则关于的方程根的情况是( )
A. 有两个相等实数根 B. 有两个不相等的实数根
C. 没有实数根 D. 无法确定
8.如图,将矩形沿对角线折叠,点的对应点为点,与交于点,其中,,则的长为( )
A.
B.
C.
D.
9.如图,在中,是的中点,点在上,连接并延长交于点,若::,,则的长为( )
A.
B.
C.
D.
10.如图,在中,是的中点,交与,已知,连接交于,下列结论:;;;;∽,其中正确的有个.
A.
B.
C.
D.
二、填空题:本题共6小题,每小题3分,共18分。
11.方程的一次项系数是______.
12.若,则 ______.
13.如图,为测量平地上一块不规则区域图中的阴影部分的面积,画一个边长为的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子假设小石子落在正方形内每一点都是等可能的,经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数附近,由此可估计不规则区域的面积是______.
14.已知线段厘米,点是线段的黄金分割点,那么线段______厘米.结果保留根号
15.设,是关于的一元二次方程的两个实数根,且,则的值为______.
16.如图,在矩形中,,点在线段上运动不含,两点,连接,以为一边在的右上方作等边三角形,连接,则线段长度的最小值为______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
解方程:
;
;
;
.
18.本小题分
如图,在中,,,在上求作一点,使得∽要求:尺规作图,不写作法,保留作图痕迹
19.本小题分
已知关于的一元二次方程.
求证:该方程总有两个不相等的实数根;
若是该方程的一个解,求方程的另一个根.
20.本小题分
如图,在四边形中,,,平分,延长至点使得,连接.
求证:四边形为菱形;
若,,求的面积.
21.本小题分
年巴黎奥运会新增了四个项目:霹雳舞,滑板,冲浪,运动攀岩,依次记为,,,,滨河体育队的小明同学把这四个项目写在了背面完全相同的卡片上将这四张卡片背面朝上,洗匀放好.
小明想从中随机抽取一张,去了解该项目在奥运会中的得分标准,恰好抽到是滑板的概率是______.
体育老师想从中选出来两个项目,让小明做成手抄报给大家普及一下,他先从中随机抽取一张不放回,再从中随机抽取一张,请用列表或画树状图的方法,求体育老师抽到的两张卡片恰好是滑板和运动攀岩的概率.
22.本小题分
如图所示,小明的爷爷想用长为米的篱笆,一面利用墙墙的最大可用长度为米,围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在上用其他材料做了宽为米的两扇小门若花圃的面积刚好为平方米.
设花圃段的长为米,则的长可表示为______米
求花圃段的长的值.
23.本小题分
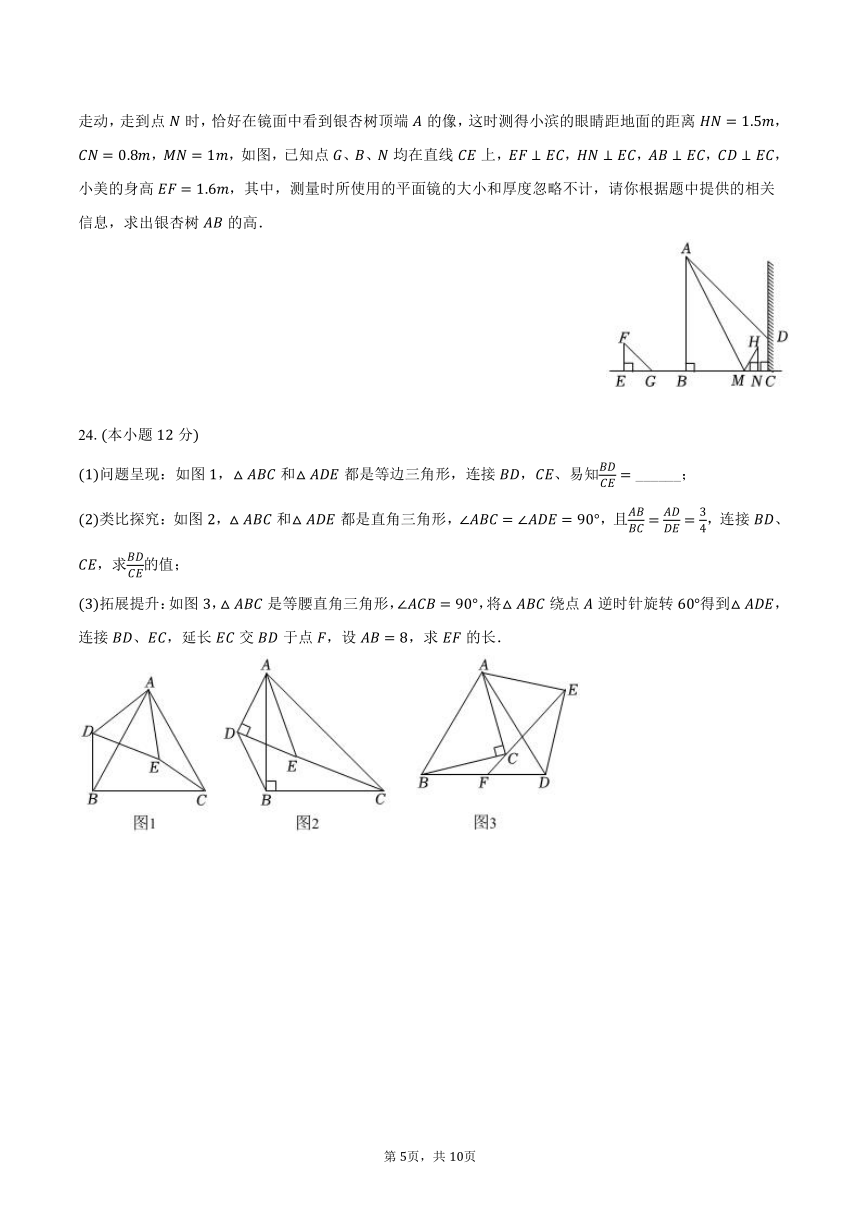
西安世博园是一个融合了古今中外园林艺术的美丽地方,让人流连忘返,它占地面积很大,拥有众多主题园区,每个园区都有独特的景观和特色在阳光明媚的一天,小滨和小美去世园会游玩,想利用所学知识测量一棵银杏树的高度银杏树四周被围起来了,底部不易到达、小滨提议用平面镜和阳光下的影子来测量银杏树的高,方法如下:首先,小滨在某一时刻测得站立在处的小美的影长,在同一时刻测量银杏树的影长时,因树靠近墙面,影子有一部分落在墙上,他测得落在墙上的影长;然后,小滨在小美和墙面之间的直线上平放一平面镜,这个平面镜在直线上的点处,镜子不动,小滨来回走动,走到点时,恰好在镜面中看到银杏树顶端的像,这时测得小滨的眼睛距地面的距离,,,如图,已知点、、均在直线上,,,,,小美的身高,其中,测量时所使用的平面镜的大小和厚度忽略不计,请你根据题中提供的相关信息,求出银杏树的高.
24.本小题分
问题呈现:如图,和都是等边三角形,连接,、易知 ______;
类比探究:如图,和都是直角三角形,,且,连接、,求的值;
拓展提升:如图,是等腰直角三角形,,将绕点逆时针旋转得到,连接、,延长交于点,设,求的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:,
开方得,,,
解得,,;
,
移项得,,
因式分解得,
,,
解得,,;
,
因式分解得,,
,,
解得,,;
,
,,,
,
,
.
18.解:如图,即为所求.
理由:,
,
平分,
,
,,
∽.
19.证明:在一元二次方程中,,,,
,
方程总有两个不相等的实数根.
解:是该方程的一个解,
,
解得,
该方程为,
解得,,
方程的另一个根为.
20.证明:,,
四边形是平行四边形,,
平分,
,
,
,
平行四边形为菱形;
解:,,
,
平分,
,
由可知,四边形为菱形,
,
,
,
,
,是等边三角形,
,,
,
,
的面积.
21.;
画树状图如下:
,
共有种等可能的结果,其中抽到的两张卡片恰好是“”和“”的结果数为,
体育老师抽到的两张卡片恰好是滑板和运动攀岩的概率.
22.;
,
化简得:,
解得:,.
当时,,不符合要求;
当时,,符合要求.
答:花圃段的长的值为.
23.解:如图,过点作 于点.
由题意可得,,
,,,
∽,
,
,
,
,,
∽,
,即,
,
樱花树的高约为.
24.;
,,
∽,
设,,
则,,
∽,
,;
,
∽,
;
如图,过点作,交的延长线于,过点作于,
是等腰直角三角形,,,
,
绕点逆时针旋转得到,
,,,,,
和都是等边三角形,
,,
,
,
,
,
又,,
≌,
,
,,
,,
,
.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程中,属于一元二次方程的是( )
A. B. C. D.
2.已知,则下列比例式正确的是( )
A. B. C. D.
3.如图,,,,,那么的长为( )
A.
B.
C.
D.
4.如图,在矩形中,对角线与相交于点,若,则的度数( )
A.
B.
C.
D.
5.在一个不透明的袋子里有红球、黄球共个,这些球除颜色外都相同,小明通过多次实验发现,摸到红球的频率稳定在左右,则袋子中红球的个数可能是( )
A. B. C. D.
6.龙年春晚主题为“龙行龘龘,欣欣家园”,“龘”这个字引发一波热门关注,据记载,“龘”出自第一部楷书字典玉篇,“龙行龘龘”形容龙腾飞的样子,昂扬而热烈某服装店购进一款印有“鬣”字图案的上衣,据店长统计,该款上衣月份销售量为件,月份销售量为件,则该款上衣销售量的月平均增长率为( )
A. B. C. D.
7.若实数,满足,则关于的方程根的情况是( )
A. 有两个相等实数根 B. 有两个不相等的实数根
C. 没有实数根 D. 无法确定
8.如图,将矩形沿对角线折叠,点的对应点为点,与交于点,其中,,则的长为( )
A.
B.
C.
D.
9.如图,在中,是的中点,点在上,连接并延长交于点,若::,,则的长为( )
A.
B.
C.
D.
10.如图,在中,是的中点,交与,已知,连接交于,下列结论:;;;;∽,其中正确的有个.
A.
B.
C.
D.
二、填空题:本题共6小题,每小题3分,共18分。
11.方程的一次项系数是______.
12.若,则 ______.
13.如图,为测量平地上一块不规则区域图中的阴影部分的面积,画一个边长为的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子假设小石子落在正方形内每一点都是等可能的,经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数附近,由此可估计不规则区域的面积是______.
14.已知线段厘米,点是线段的黄金分割点,那么线段______厘米.结果保留根号
15.设,是关于的一元二次方程的两个实数根,且,则的值为______.
16.如图,在矩形中,,点在线段上运动不含,两点,连接,以为一边在的右上方作等边三角形,连接,则线段长度的最小值为______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
解方程:
;
;
;
.
18.本小题分
如图,在中,,,在上求作一点,使得∽要求:尺规作图,不写作法,保留作图痕迹
19.本小题分
已知关于的一元二次方程.
求证:该方程总有两个不相等的实数根;
若是该方程的一个解,求方程的另一个根.
20.本小题分
如图,在四边形中,,,平分,延长至点使得,连接.
求证:四边形为菱形;
若,,求的面积.
21.本小题分
年巴黎奥运会新增了四个项目:霹雳舞,滑板,冲浪,运动攀岩,依次记为,,,,滨河体育队的小明同学把这四个项目写在了背面完全相同的卡片上将这四张卡片背面朝上,洗匀放好.
小明想从中随机抽取一张,去了解该项目在奥运会中的得分标准,恰好抽到是滑板的概率是______.
体育老师想从中选出来两个项目,让小明做成手抄报给大家普及一下,他先从中随机抽取一张不放回,再从中随机抽取一张,请用列表或画树状图的方法,求体育老师抽到的两张卡片恰好是滑板和运动攀岩的概率.
22.本小题分
如图所示,小明的爷爷想用长为米的篱笆,一面利用墙墙的最大可用长度为米,围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在上用其他材料做了宽为米的两扇小门若花圃的面积刚好为平方米.
设花圃段的长为米,则的长可表示为______米
求花圃段的长的值.
23.本小题分
西安世博园是一个融合了古今中外园林艺术的美丽地方,让人流连忘返,它占地面积很大,拥有众多主题园区,每个园区都有独特的景观和特色在阳光明媚的一天,小滨和小美去世园会游玩,想利用所学知识测量一棵银杏树的高度银杏树四周被围起来了,底部不易到达、小滨提议用平面镜和阳光下的影子来测量银杏树的高,方法如下:首先,小滨在某一时刻测得站立在处的小美的影长,在同一时刻测量银杏树的影长时,因树靠近墙面,影子有一部分落在墙上,他测得落在墙上的影长;然后,小滨在小美和墙面之间的直线上平放一平面镜,这个平面镜在直线上的点处,镜子不动,小滨来回走动,走到点时,恰好在镜面中看到银杏树顶端的像,这时测得小滨的眼睛距地面的距离,,,如图,已知点、、均在直线上,,,,,小美的身高,其中,测量时所使用的平面镜的大小和厚度忽略不计,请你根据题中提供的相关信息,求出银杏树的高.
24.本小题分
问题呈现:如图,和都是等边三角形,连接,、易知 ______;
类比探究:如图,和都是直角三角形,,且,连接、,求的值;
拓展提升:如图,是等腰直角三角形,,将绕点逆时针旋转得到,连接、,延长交于点,设,求的长.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:,
开方得,,,
解得,,;
,
移项得,,
因式分解得,
,,
解得,,;
,
因式分解得,,
,,
解得,,;
,
,,,
,
,
.
18.解:如图,即为所求.
理由:,
,
平分,
,
,,
∽.
19.证明:在一元二次方程中,,,,
,
方程总有两个不相等的实数根.
解:是该方程的一个解,
,
解得,
该方程为,
解得,,
方程的另一个根为.
20.证明:,,
四边形是平行四边形,,
平分,
,
,
,
平行四边形为菱形;
解:,,
,
平分,
,
由可知,四边形为菱形,
,
,
,
,
,是等边三角形,
,,
,
,
的面积.
21.;
画树状图如下:
,
共有种等可能的结果,其中抽到的两张卡片恰好是“”和“”的结果数为,
体育老师抽到的两张卡片恰好是滑板和运动攀岩的概率.
22.;
,
化简得:,
解得:,.
当时,,不符合要求;
当时,,符合要求.
答:花圃段的长的值为.
23.解:如图,过点作 于点.
由题意可得,,
,,,
∽,
,
,
,
,,
∽,
,即,
,
樱花树的高约为.
24.;
,,
∽,
设,,
则,,
∽,
,;
,
∽,
;
如图,过点作,交的延长线于,过点作于,
是等腰直角三角形,,,
,
绕点逆时针旋转得到,
,,,,,
和都是等边三角形,
,,
,
,
,
,
又,,
≌,
,
,,
,,
,
.
第1页,共1页
同课章节目录
