6.6 余角和补角 课件(共18张PPT)青岛版数学七年级上册
文档属性
| 名称 | 6.6 余角和补角 课件(共18张PPT)青岛版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 650.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-18 09:32:19 | ||
图片预览


文档简介
(共18张PPT)
6.6 余角和补角
第6章 基本的几何图形
O
A
B
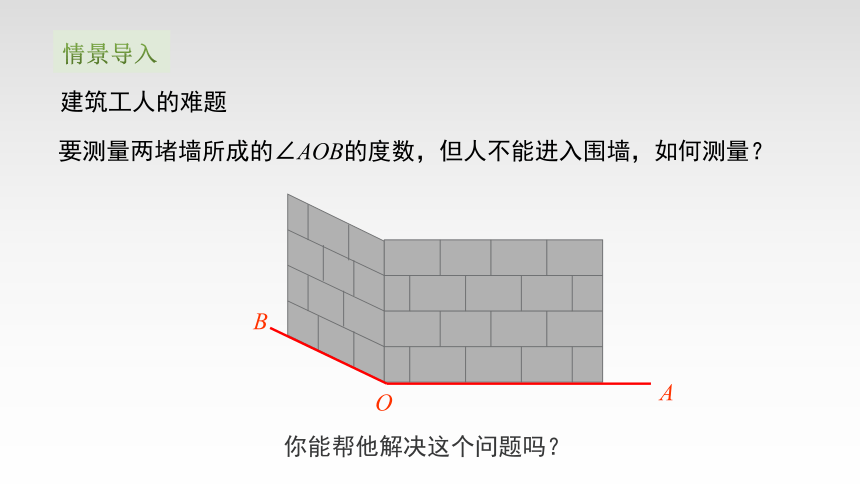
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量?
建筑工人的难题
你能帮他解决这个问题吗?
情景导入
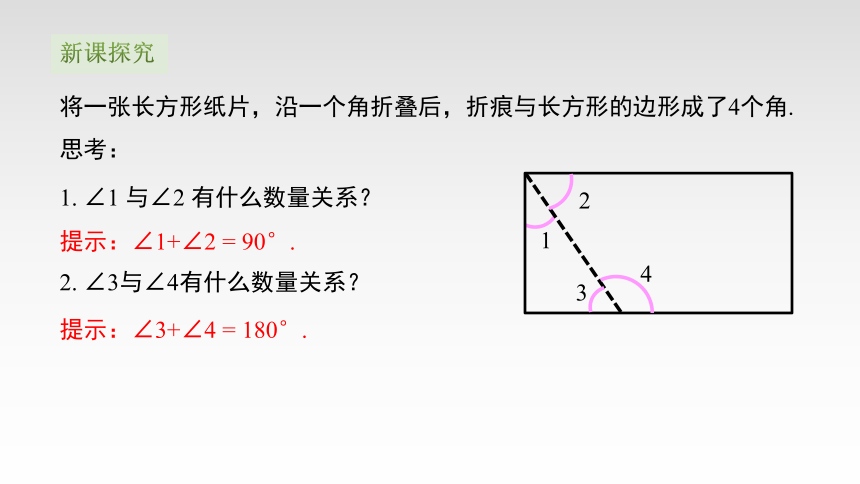
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
思考:
1. ∠1 与∠2 有什么数量关系?
提示:∠1+∠2 = 90°.
2. ∠3与∠4有什么数量关系?
提示:∠3+∠4 = 180°.
1
2
3
4
新课探究
余角的概念
1
如果两个角的和等于90°(直角),就说这两个角互为余角 (简称为两个角互余).
如图,可以说 ∠1 是 ∠2 的余角,
或 ∠2 是∠1的余角,
或 ∠1和 ∠2互余.
2
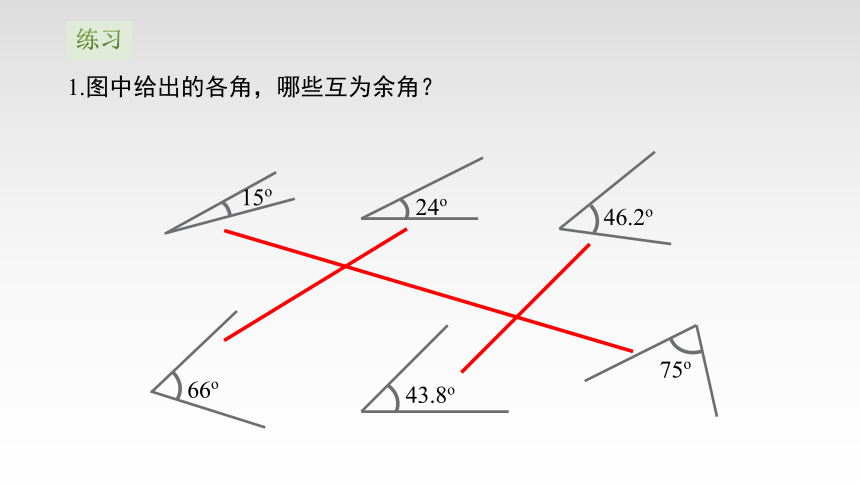
1.图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
练习
补角的概念
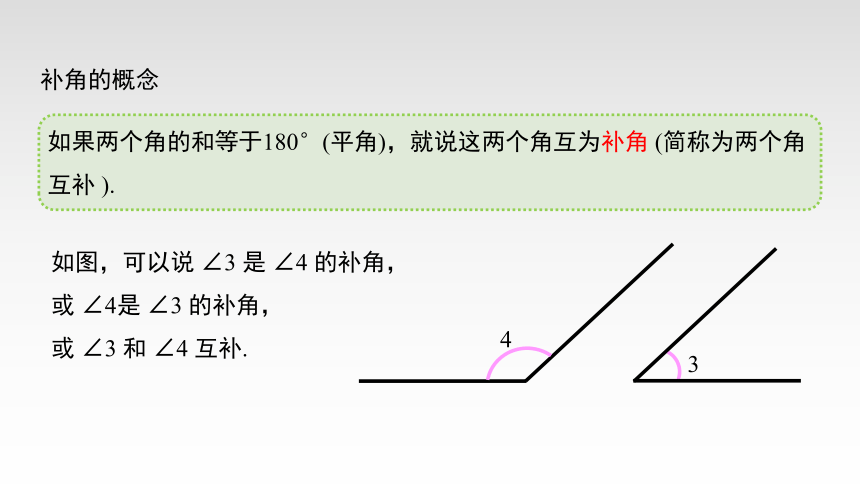
如果两个角的和等于180°(平角),就说这两个角互为补角 (简称为两个角互补 ).
如图,可以说 ∠3 是 ∠4 的补角,
或 ∠4是 ∠3 的补角,
或 ∠3 和 ∠4 互补.
4
3
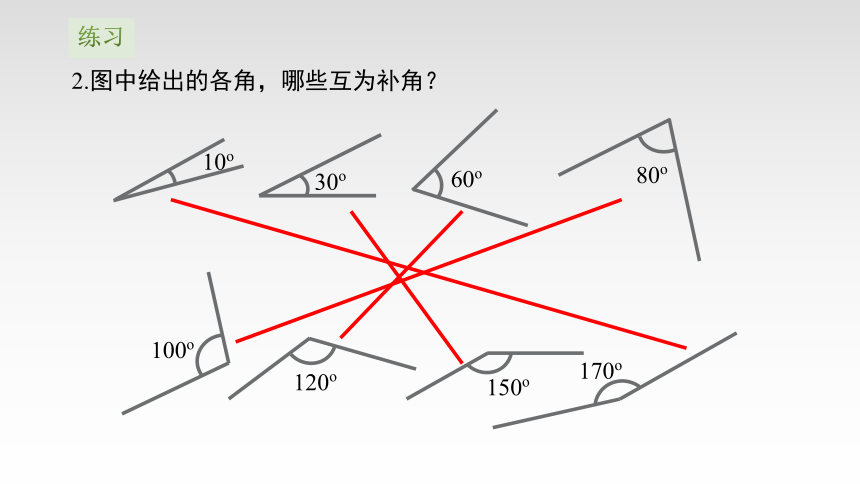
2.图中给出的各角,哪些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
练习
要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量?
A
B
O
C
D
解释生活
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
x°(0<x<90)
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
(90-x)°
(180-x)°
观察可得结论:锐角的补角比它的余角大_____.
90°
填表并思考
余角和补角的性质
∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
思考:
1
2
同角 (等角) 的补角相等.
结论:
3
∠2=180°-∠1
∠3=180°-∠1
同角 (等角) 的余角相等.
类似地,可以得到:
=
1.若一个角为65°,则它的补角的度数为( )
A.25° B.35° C.115° D.125°
2.与30°的角互为余角的角的度数是( )
A.30° B.60° C.70° D.90°
3.下列各图中,∠1与∠2互为余角的是( )
C
B
B
互动合作
4.一个角比它的余角大10°,这个角为( )
A.40° B.45° C.50° D.55°
5.下列说法正确的是( )
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
C
D
互动合作
6.下列说法中,正确的有________.(填序号)
①钝角与锐角互补;
②∠α的余角是90°-∠α;
③∠β的补角是180°-∠β;
④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
②③
互动合作
7.已知一个角的补角是这个角的余角的4倍,求这个角的度数.
解:设这个角为x度,则这个角的余角是(90-x) 度,
补角是(180-x)度,
由题意得,
180-x=4(90-x),
解得x=60,
答:这个角的度数为60°.
互动合作
解:设∠2=x,则∠1=x+20,
由题意得:
∠1+∠2=x+20+x=180,
∴x=80°,
∴∠2=80°,
∠1=x+20°=100°.
8.已知∠1与∠2互为补角,且∠1比∠2大20°,求∠1、∠2的度数.
互动合作
9.如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是______________,∠COD的余角是_______________;
(2)OE是∠BOC的平分线吗?请说明理由.
∠COE、∠BOE
O
A
B
C
D
E
∠COE、∠BOE
解: (2) OE平分∠BOC,
理由如下:∵∠DOE=90°,∴∠AOD+∠BOE=90°,
∴∠COD+∠COE=90°,
∴∠AOD+∠BOE=∠COD+∠COE,
∵OD平分∠AOC,∴∠AOD=∠COD,
∴∠COE=∠BOE,∴OE平分∠BOC.
概念 定义 数量关系 共同点
互为余角 (互余)
互为补角 (互补) 如果两个锐角的和是一个直角,我们就说这两个角互为余角,也可以说其中一个角是另一个角的余角.
如果两个角的和是一个平角,我们就说这两个角互为补角,也可以说其中一个角是另一个角的补角.
①互余、互补是两个角的关系;
②互余、互补只跟角的大小有关,与位置无关.
课堂小结
本课结束
6.6 余角和补角
第6章 基本的几何图形
O
A
B
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量?
建筑工人的难题
你能帮他解决这个问题吗?
情景导入
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角.
思考:
1. ∠1 与∠2 有什么数量关系?
提示:∠1+∠2 = 90°.
2. ∠3与∠4有什么数量关系?
提示:∠3+∠4 = 180°.
1
2
3
4
新课探究
余角的概念
1
如果两个角的和等于90°(直角),就说这两个角互为余角 (简称为两个角互余).
如图,可以说 ∠1 是 ∠2 的余角,
或 ∠2 是∠1的余角,
或 ∠1和 ∠2互余.
2
1.图中给出的各角,哪些互为余角?
15o
24o
66o
75o
46.2o
43.8o
练习
补角的概念
如果两个角的和等于180°(平角),就说这两个角互为补角 (简称为两个角互补 ).
如图,可以说 ∠3 是 ∠4 的补角,
或 ∠4是 ∠3 的补角,
或 ∠3 和 ∠4 互补.
4
3
2.图中给出的各角,哪些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
练习
要测量两堵墙所成的角的度数,但人不能进入围墙,如何测量?
A
B
O
C
D
解释生活
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
x°(0<x<90)
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
(90-x)°
(180-x)°
观察可得结论:锐角的补角比它的余角大_____.
90°
填表并思考
余角和补角的性质
∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系?
思考:
1
2
同角 (等角) 的补角相等.
结论:
3
∠2=180°-∠1
∠3=180°-∠1
同角 (等角) 的余角相等.
类似地,可以得到:
=
1.若一个角为65°,则它的补角的度数为( )
A.25° B.35° C.115° D.125°
2.与30°的角互为余角的角的度数是( )
A.30° B.60° C.70° D.90°
3.下列各图中,∠1与∠2互为余角的是( )
C
B
B
互动合作
4.一个角比它的余角大10°,这个角为( )
A.40° B.45° C.50° D.55°
5.下列说法正确的是( )
A.一个角的补角一定大于它本身
B.一个角的余角一定小于它本身
C.一个钝角减去一个锐角的差一定是一个锐角
D.一个角的余角一定小于其补角
C
D
互动合作
6.下列说法中,正确的有________.(填序号)
①钝角与锐角互补;
②∠α的余角是90°-∠α;
③∠β的补角是180°-∠β;
④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
②③
互动合作
7.已知一个角的补角是这个角的余角的4倍,求这个角的度数.
解:设这个角为x度,则这个角的余角是(90-x) 度,
补角是(180-x)度,
由题意得,
180-x=4(90-x),
解得x=60,
答:这个角的度数为60°.
互动合作
解:设∠2=x,则∠1=x+20,
由题意得:
∠1+∠2=x+20+x=180,
∴x=80°,
∴∠2=80°,
∠1=x+20°=100°.
8.已知∠1与∠2互为补角,且∠1比∠2大20°,求∠1、∠2的度数.
互动合作
9.如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是______________,∠COD的余角是_______________;
(2)OE是∠BOC的平分线吗?请说明理由.
∠COE、∠BOE
O
A
B
C
D
E
∠COE、∠BOE
解: (2) OE平分∠BOC,
理由如下:∵∠DOE=90°,∴∠AOD+∠BOE=90°,
∴∠COD+∠COE=90°,
∴∠AOD+∠BOE=∠COD+∠COE,
∵OD平分∠AOC,∴∠AOD=∠COD,
∴∠COE=∠BOE,∴OE平分∠BOC.
概念 定义 数量关系 共同点
互为余角 (互余)
互为补角 (互补) 如果两个锐角的和是一个直角,我们就说这两个角互为余角,也可以说其中一个角是另一个角的余角.
如果两个角的和是一个平角,我们就说这两个角互为补角,也可以说其中一个角是另一个角的补角.
①互余、互补是两个角的关系;
②互余、互补只跟角的大小有关,与位置无关.
课堂小结
本课结束
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
