2024~2025学年沪教版六年级数学上册 1.1.2 数轴 课件(16张PPT)
文档属性
| 名称 | 2024~2025学年沪教版六年级数学上册 1.1.2 数轴 课件(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-18 10:15:09 | ||
图片预览






文档简介
(共16张PPT)
沪教版(2024)六年级数学上册
1.1 有理数的引入
第二课时
数轴
第一章 有理数
内容回顾
上节课我们学习了正数和负数,我们一起复习一下
1.正数和负数可以表示相反意义的量;
2.数字前面有“+”号(正号)或没有符号的数是正数(0除外);
数字前面有“-”号(负号)的数是负数;
零既不是正数也不是负数!
5.非负数指零和正数;非正数指零和负数;
6.非负整数指零和正整数;非正整数指零和负整数.
3.正整数、零和负整数统称为整数;
4.能够写成分数 (a、b是整数,a≠0)的数叫作有理数;
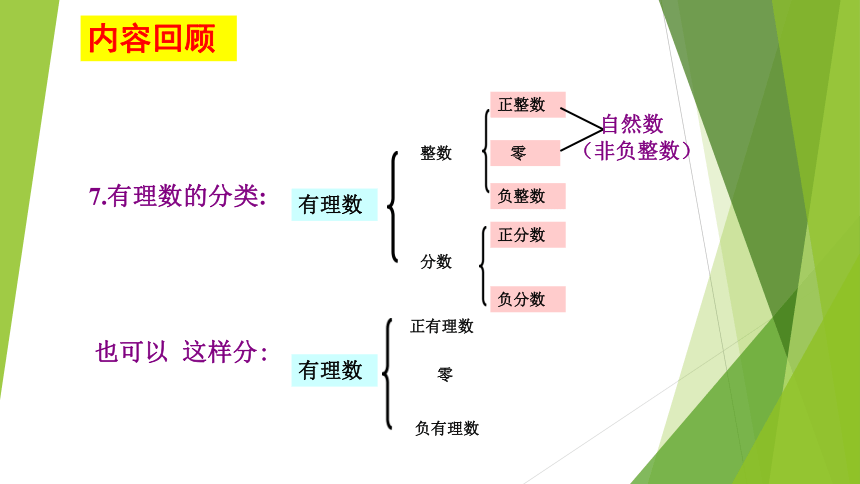
7.有理数的分类:
整数
零
分数
正整数
正分数
负整数
负分数
有理数
自然数
(非负整数)
正有理数
零
负有理数
有理数
也可以 这样分:
内容回顾
一、掌握数轴的三要素,并能熟练的画出数轴;
二、可以说出数轴上的点所表示的数;可以在数轴上标记出任意有理数;
三、数形结合,理解有理数与数轴上的点的对应关系,初步了解数形结合的数学思想;
学习目标
我们已经知道,零上温度用正数表示,零下温度用负数表示,如图1-1-7所示。
把温度计水平横置,那么在“0”右边的数都是正数,在“0”的左边都是负数。
情景导入
思考
我们能否仿照温度计,用水平直线上的一些点来表示正数、负数和0?
小海家在学校的正东方向,距离学校3km,小华家在学校的正西方向,距离学校4Km.试画图表示这一个情境。
分析:若以学校为基准,规定”正东方向”为正,那么学校可以用0km表示,小海家可以用+3km表示,小华家可以用-4km表示。
操作
如图1-1-8所示:
1、画一条直线,从左往右表示从西到东的方向,在直线上任取一个点O表示学校的位置;
2、规定一个单位长度(线段0A的长)代表1km;
3、于是,在点O右边,与点O距离3个单位长度的点B表示小海家的位置;
4、在点O左边,与点O距离4个单位长度的点C表示小华家的位置。
这样,0可以用直线上的点O表示,+3和-4分别可以用直线上的点B和点C表示。
归纳总结
如图1-1-9
1、画一条直线(一般画成水平的直线),在直线上任取一点表示0,把这个点叫作原点;
2、规定直线的一个方向(一般取从左往右的方向)为正方向,并用箭头表示;
3、再选取适当的长度作为一个单位长度;
4、在直线上,从原点向右,每隔一个单位长度取一个点,依次表示为1、2、3等;从原点往左,用类似的方法依次取点,并表示为-1,-2,-3等。
定义:像这样规定了原点、正方向和单位长度的直线叫作数轴。
应用
有了数轴,我们怎么使用它呢?
例如,2可以用数轴上位于原点右边、距离原点2个单位长度的点来表示;
3.4 可以用数轴上位于原点右边、距离原点3.4个单位长度的点来表示;
-3可以用数轴上位于原点左边、距离原点3个单位长度的点来表示;
-可以用数轴上位于原点右边、距离原点个单位长度的点来表示;
任何有理数,都可以用数轴上点表示。
反过来说,“数轴上的点表示的都是有理数”是错误的!
3.4
应用
例1
下图中,这些都是数轴吗?若不是,请说明理由.
缺少原点
箭头方向错误
缺少正方向
缺少单位长度
应用
例2 指出下图数轴上的点A、B、C、D、E 、F分
别表示什么数.
点E表示 ,
点D表示 ,
点F表示 .
解:点A表示2,
点B表示5,
点C表示-1,
A
F
E
C
B
D
用分数和小数表示均可
应用
例3 画一条数轴,并用数轴上的点表示下列各数:
3,-3, 0.5,-0.5, 1, - 1
解:如图所示
0.5
3
1
-1
-3
-0.5
应用
例4 数轴上有一点P,点P在数轴的2处,将点P
先向右移动3个单位长度,再向左移动6个单位长度,
那么终点所表示的数是多少?
解:如图所示
P
所以,终点表示的数为-1.
数形结合 是一种数学思想方法,通过数与形之间的对应和转化来解决数学问题。
应用
例5 A,B两点在数轴上,点A表示4,点B表示-3,则线段AB长度是多少?
解:如图所示,将A、B所表示的数在数轴上表示出来:
A
所以,线段AB的长度是7.
B
应用
例5 A,B两点在数轴上,点A表示1,线段AB长度为4,则B点表示的数是多少?
解:如图所示,将A所表示的数在数轴上表示出来,将A点向右平移4个单位得到B1 ,将A点向左平移4个单位得到B2 ,
A
所以,B点表示的数是5或-3.
B2
B1
课堂小结
通过这节课的学习,你有哪些收获与体会?
1.数轴的定义:我们把规定了原点、正方向和单位长度的直线叫作数轴。
数轴的三要素:原点、正方向和单位长度;
2.任何有理数,都可以用数轴上点表示。
反过来说,“数轴上的点表示的都是有理数”是错误的!
3.数形结合 是一种数学思想方法,通过数与形之间的对应和转化来解决数学问题。
THANKS
沪教版(2024)六年级数学上册
1.1 有理数的引入
第二课时
数轴
第一章 有理数
内容回顾
上节课我们学习了正数和负数,我们一起复习一下
1.正数和负数可以表示相反意义的量;
2.数字前面有“+”号(正号)或没有符号的数是正数(0除外);
数字前面有“-”号(负号)的数是负数;
零既不是正数也不是负数!
5.非负数指零和正数;非正数指零和负数;
6.非负整数指零和正整数;非正整数指零和负整数.
3.正整数、零和负整数统称为整数;
4.能够写成分数 (a、b是整数,a≠0)的数叫作有理数;
7.有理数的分类:
整数
零
分数
正整数
正分数
负整数
负分数
有理数
自然数
(非负整数)
正有理数
零
负有理数
有理数
也可以 这样分:
内容回顾
一、掌握数轴的三要素,并能熟练的画出数轴;
二、可以说出数轴上的点所表示的数;可以在数轴上标记出任意有理数;
三、数形结合,理解有理数与数轴上的点的对应关系,初步了解数形结合的数学思想;
学习目标
我们已经知道,零上温度用正数表示,零下温度用负数表示,如图1-1-7所示。
把温度计水平横置,那么在“0”右边的数都是正数,在“0”的左边都是负数。
情景导入
思考
我们能否仿照温度计,用水平直线上的一些点来表示正数、负数和0?
小海家在学校的正东方向,距离学校3km,小华家在学校的正西方向,距离学校4Km.试画图表示这一个情境。
分析:若以学校为基准,规定”正东方向”为正,那么学校可以用0km表示,小海家可以用+3km表示,小华家可以用-4km表示。
操作
如图1-1-8所示:
1、画一条直线,从左往右表示从西到东的方向,在直线上任取一个点O表示学校的位置;
2、规定一个单位长度(线段0A的长)代表1km;
3、于是,在点O右边,与点O距离3个单位长度的点B表示小海家的位置;
4、在点O左边,与点O距离4个单位长度的点C表示小华家的位置。
这样,0可以用直线上的点O表示,+3和-4分别可以用直线上的点B和点C表示。
归纳总结
如图1-1-9
1、画一条直线(一般画成水平的直线),在直线上任取一点表示0,把这个点叫作原点;
2、规定直线的一个方向(一般取从左往右的方向)为正方向,并用箭头表示;
3、再选取适当的长度作为一个单位长度;
4、在直线上,从原点向右,每隔一个单位长度取一个点,依次表示为1、2、3等;从原点往左,用类似的方法依次取点,并表示为-1,-2,-3等。
定义:像这样规定了原点、正方向和单位长度的直线叫作数轴。
应用
有了数轴,我们怎么使用它呢?
例如,2可以用数轴上位于原点右边、距离原点2个单位长度的点来表示;
3.4 可以用数轴上位于原点右边、距离原点3.4个单位长度的点来表示;
-3可以用数轴上位于原点左边、距离原点3个单位长度的点来表示;
-可以用数轴上位于原点右边、距离原点个单位长度的点来表示;
任何有理数,都可以用数轴上点表示。
反过来说,“数轴上的点表示的都是有理数”是错误的!
3.4
应用
例1
下图中,这些都是数轴吗?若不是,请说明理由.
缺少原点
箭头方向错误
缺少正方向
缺少单位长度
应用
例2 指出下图数轴上的点A、B、C、D、E 、F分
别表示什么数.
点E表示 ,
点D表示 ,
点F表示 .
解:点A表示2,
点B表示5,
点C表示-1,
A
F
E
C
B
D
用分数和小数表示均可
应用
例3 画一条数轴,并用数轴上的点表示下列各数:
3,-3, 0.5,-0.5, 1, - 1
解:如图所示
0.5
3
1
-1
-3
-0.5
应用
例4 数轴上有一点P,点P在数轴的2处,将点P
先向右移动3个单位长度,再向左移动6个单位长度,
那么终点所表示的数是多少?
解:如图所示
P
所以,终点表示的数为-1.
数形结合 是一种数学思想方法,通过数与形之间的对应和转化来解决数学问题。
应用
例5 A,B两点在数轴上,点A表示4,点B表示-3,则线段AB长度是多少?
解:如图所示,将A、B所表示的数在数轴上表示出来:
A
所以,线段AB的长度是7.
B
应用
例5 A,B两点在数轴上,点A表示1,线段AB长度为4,则B点表示的数是多少?
解:如图所示,将A所表示的数在数轴上表示出来,将A点向右平移4个单位得到B1 ,将A点向左平移4个单位得到B2 ,
A
所以,B点表示的数是5或-3.
B2
B1
课堂小结
通过这节课的学习,你有哪些收获与体会?
1.数轴的定义:我们把规定了原点、正方向和单位长度的直线叫作数轴。
数轴的三要素:原点、正方向和单位长度;
2.任何有理数,都可以用数轴上点表示。
反过来说,“数轴上的点表示的都是有理数”是错误的!
3.数形结合 是一种数学思想方法,通过数与形之间的对应和转化来解决数学问题。
THANKS
同课章节目录
