1.2时间的测量(课件)(共38张PPT) -八年级物理上册同步精品课堂(沪科版(五四学制)2024)
文档属性
| 名称 | 1.2时间的测量(课件)(共38张PPT) -八年级物理上册同步精品课堂(沪科版(五四学制)2024) |  | |
| 格式 | pptx | ||
| 文件大小 | 39.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-18 14:48:56 | ||
图片预览








文档简介
(共38张PPT)
沪科版(五·四学制) 八年级上册
第1章 测量
1.2 时间的测量
如图 1-2-1 所示, 地铁站台显示屏上的信息预告了地铁到站的时间,方便乘客安排行程。 随着信息技术的发展,人们获知时间的方式变得越来越便捷。用刻度尺可以测量长度,用什么工具来测量时间呢?
情景引入
01
02
03
04
05
CONTENTS
图表法、数轴记录时间
古代测量时间 摆的等时性
时间的单位与换算
时间的测量
PART ONE
古代测量时间 摆的等时性
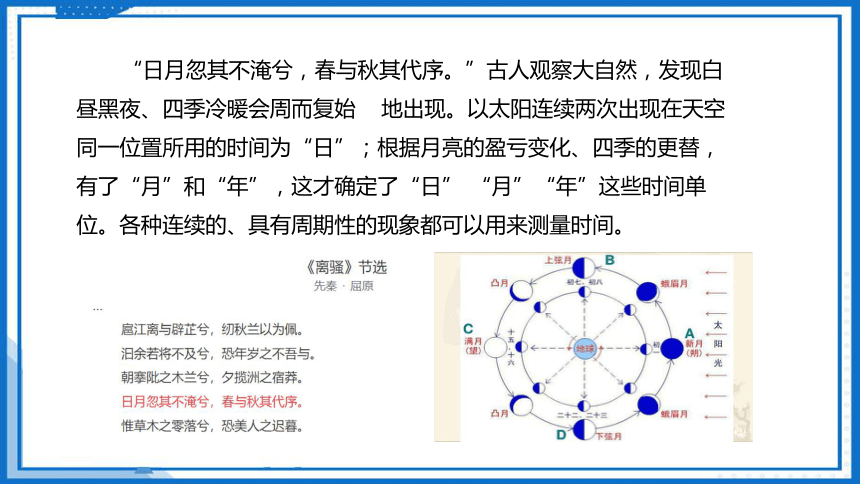
“日月忽其不淹兮,春与秋其代序。”古人观察大自然,发现白昼黑夜、四季冷暖会周而复始 地出现。以太阳连续两次出现在天空同一位置所用的时间为“日”;根据月亮的盈亏变化、四季的更替,有了“月”和“年”,这才确定了“日” “月”“年”这些时间单位。各种连续的、具有周期性的现象都可以用来测量时间。
“时”和“刻”是比年、月、日更小的时间单位。如图 1-2-3 所示, 为了满足生产、生活的需要,古人发明了日晷、漏刻等工具来测量时间。日晷利用一天中不同时刻晷针影子的位置变将晷面划分为十二时辰。
一炷香的时间
沙漏
思考:古人还有哪些测量时间的方式?
图 1-2-2 中的现象是否可以用来测量时间?
想一想
主要贡献:
发现摆的等时性
与培根提出科学实验方法
提出相对性原理
发明望远镜(伽利略望远镜)
发明最早的温度计
美誉:
现代观测天文学之父
现代物理学之父
科学之父
现代科学之父
1583 年,意大利物理学家伽利略(G. Galilei, 1564— 1642)发现同一吊灯完成一次摆动的时间大致相同。以此为基础,荷兰物理学家惠更斯 ( C. Huygens , 1629— 1695)发明了摆钟, 摆钟经不断改进沿用至今。
01.发现问题,提出假设
事情发生在400多年前的意大利比萨,年轻的伽利略当时在比萨大学学习。有一天,伽利略在教堂里发现穹顶上挂的吊灯不停地来回摆动,这本是司空见惯的现象却引起了伽利略的注意。他发现尽管吊灯摆动的幅度越来越小,但每摆动一次的时间似乎是相等的。这个现象令他大为惊奇,于是他决定仔细地观察。
提出假设:单摆的周期可能与摆球的质量、摆线的长度、摆动幅度有关。
02.设计实验
1.实验目的:探究单摆的周期与哪些因素有关
2.实验器材:不同质量(100克和200克)的摆球、不同长度(80厘米和40厘米)的摆线
3.实验步骤:
①探究单摆的周期是否与摆球的质量有关
(取长度相同的摆线,质量不同的摆球,在与竖直方向夹角相同处释放,测量摆动周期)
②探究单摆的周期是否与摆线的长度有关
(取长度不同的摆线,质量相同的摆球,在与竖直方向夹角相同处释放,测量摆动周期)
③探究单摆的周期是否与摆动幅度有关
(取长度相同的摆线,质量相同的摆球,在与竖直方向夹角不同处释放,测量摆动周期)
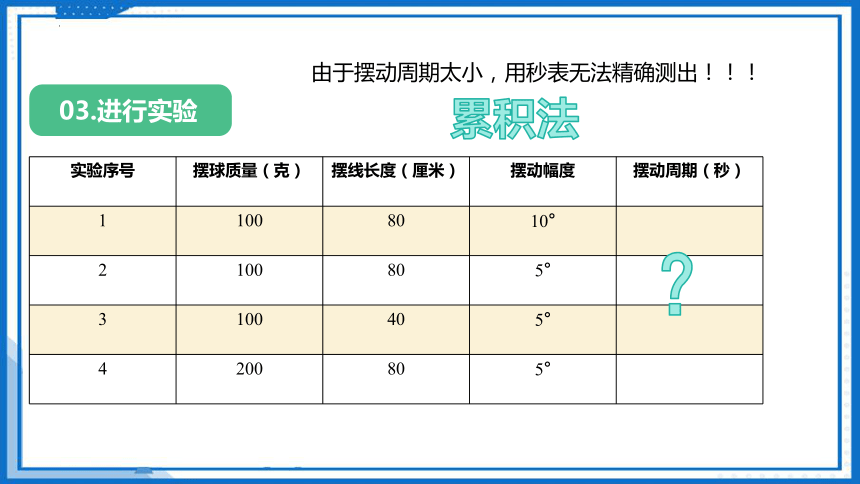
03.进行实验
实验序号 摆球质量(克) 摆线长度(厘米) 摆动幅度 摆动周期(秒)
1 100 80 10°
2 100 80 5°
3 100 40 5°
4 200 80 5°
由于摆动周期太小,用秒表无法精确测出!!!
?
累积法
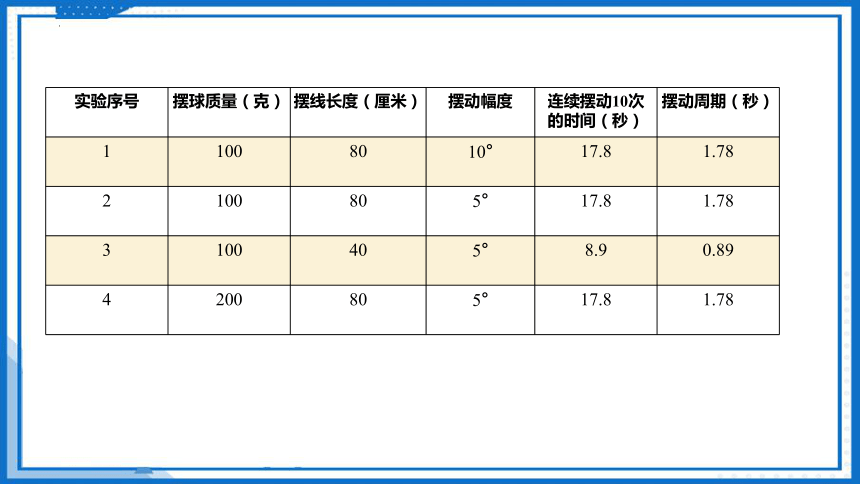
03.进行实验
实验序号 摆球质量(克) 摆线长度(厘米) 摆动幅度 连续摆动10次的时间(秒) 摆动周期(秒)
1 100 80 10° 17.8 1.78
2 100 80 5° 17.8 1.78
3 100 40 5° 8.9 0.89
4 200 80 5° 17.8 1.78
04.归纳得到结论
实验序号 摆球质量(克) 摆线长度(厘米) 摆动幅度 连续摆动10次的时间(秒) 摆动周期(秒)
1 100 80 10° 17.8 1.78
4 200 80 5° 17.8 1.78
摆动周期与摆球质量的关系
分析实验序号1和4,可以得到的结论是:
________________________________________________________________________________
当摆线长度、摆动幅度相同时,摆动周期与摆球质量无关
条件+结论
摆动周期与摆线长度的关系
分析实验序号2和3,可以得到的结论是:
________________________________________________________________________________
当摆球质量、摆动幅度相同时,摆动周期与摆线长度有关
实验序号 摆球质量(克) 摆线长度(厘米) 摆动幅度 连续摆动10次的时间(秒) 摆动周期(秒)
2 100 80 5° 17.8 1.78
3 100 40 5° 8.9 0.89
←正确但不完整
摆线长度越长,摆动周期越长
04.归纳得到结论
摆动周期与摆动幅度的关系
分析实验序号1和2,可以得到的结论是:
________________________________________________________________________________
当摆球质量、摆线长度相同时,摆动周期与摆动幅度无关
实验序号 摆球质量(克) 摆线长度(厘米) 摆动幅度 连续摆动10次的时间(秒) 摆动周期(秒)
1 100 80 10° 17.8 1.78
2 100 80 5° 17.8 1.78
04.归纳得到结论
摆动周期只与_______________________有关
摆线长度
因此,图 1-2-2 中的荡秋千、摩天轮是可以用来测量时间的。
PART TWO
时间的单位与换算 时间的测量
在物理学中, 时间用字母t 表示。在国际单位制中, 时间的基本单位是秒( second),符号是s。人们曾根据地球自转等天文现象来确定 1 s 的长短。目前以铯原子的振动为基准来确定1 s 的长短。铯原子钟非常稳定,几千万年才相差 1 s。
比秒大的单位有分(min)、时(h), 比秒小的单位有毫秒( ms )和微秒(μs),它们与秒之间的换算关系如下:
1 h = 3 600 s
1 min = 60 s
1 ms = 10-3 s
1 μs = 10-6 s
现代测量时间工具:机械钟表、石英钟、秒表等
我们通常用时钟、手表和秒表等工具来测量时间。时钟的最小单位是分, 手表的最小单位一般是秒,使用电子秒表计时最小单 位可以到百分之一秒。记录短跑成绩时,就会用到比时钟、手表更精确的秒表。
石英钟
秒表
机械停表
电子手表
(1)量程和分度值:机械停表的外圈(大表盘)以秒为单位,内圈(小表盘)以分为单位,不同停表量程和分度值会不同,量程以小圈为准。如图中小表盘转一圈量程为60 min,外圈分度值为0.2 s。
机械停表的使用
(2)测量方法:
01
调零:使用前若指针未与零刻度线对齐,则根据停表的实际结构按动“复位”按钮进行归零
02
启动:先上好发条,用手握住停表,大拇指按下“开始/停止”按钮,开始计时
03
停止:再次按下“开始/停止”按钮,停表指针停止走动,结束计时
04
读数
(3)读数:在读数时,先读出小表盘上指针所通过的分钟数(按整数读);再观察小表盘上的指针有没有超过两数字之间的半分钟刻度线,若不超过,则大表盘按照0~30s读数,若超过,则大表盘按照31~60s读数。左图读数是5分钟37.5秒。换成秒是:337.5秒
如图,秒表的读数是 s。
活动探究
课代表分发秒表、多功能电子表,分小组操作练习。
活动:连续击掌10次,同学们用秒表和多功能电子表同时计时测量。
随讲随练
275.2
观察电子秒表
1. 观察实验室提供的电子秒表,它的最小单位是什么?
2. 电子秒表的“启动”“暂停”和“归零”按钮在哪里?
学习使用电子秒表
在计时模式下,按下“启动”按钮,电子秒表开始计时。按下“暂停”按 钮, 电子秒表停止计时,屏幕上会显示记录的时间。按下“归零”按钮后电子秒表显示的时间会重置为零。大部分电子秒表有分段计时功能,不仅可以将整 个计时过程分解,还可以递加计时。
用电子秒表测量时间
用电子秒表测量脉搏跳动 30 次的时间
测量脉搏跳动 30 次所用的时间,将测量结果填入表 1-2-1 中。
序号 脉搏跳动 30 次所用的时间 /s
1
2
3
脉搏跳动 30 次所用时间的平均值: s
交流讨论
由上述测量结果能否知道脉搏跳动一次的时间?
为什么不用电子秒表直接测量脉搏跳动一次的时间?
PART THREE
图表法、数轴记录时间
图1-2-5 是苹果下落过程中依次经过位置A 、B 、C、D 、E、F 的照片, 它是每隔0.1 s 拍摄一次而得。表1-2-2 记录了苹果从图中位置 A 到其他各个位置所用的时间。
位置 A B C D E F
运动时间 /s 0 0.1 0.2 0.3 0.4 0.5
表 1-2-2 数据记录表
我们也可以把苹果下落的时间信息记录在数轴上。图1-2-6 中的tAD 表示苹果从位置 A 下落 到位置 D 所用的时间,线段 AD 的长度可以直观地表示tAD 的长短。
1.每周一庄严的升旗礼上,我们要唱国歌、行注目礼。此环节国歌演奏的时长约为 ( )
A . 0.5s B .5s
C .50s D . 5min
课堂练习
C
2 .下列过程中,经历的时间差不多为 1 秒的是 ( )
A .人的眼睛眨一下的时间
B .人呼吸一次的时间
C .人的心脏跳动一次的时间
D .人行走 5 米路程所需的时间
C
日晷
卷尺
3 .下列工具不能用来计时的是 ( )
A .
C .
B .
D .
电子手表
沙漏
C
4 .如图,停表的读数为 s。
220.5
5 .为了研究单摆摆动的周期与摆线长度的关系,应保持 ( )
A .摆线的长度和摆球的质量不变,改变摆动的幅度
B .摆线的长度和摆动的幅度不变,改变摆球的质量
C .摆动的幅度和摆球的质量不变,改变摆线的长度
D .摆动的幅度和摆球的质量,摆线的长度都不变,改变摆球的形状
C
6 .周末上午李妍同学在开始写作业时看了一下表,表的指针如图甲所示;李妍写完作业之后又看了一次表,此时表的指针如图乙所示(时间都是上午),则李妍写作业所用的时间为( )
A .1 个小时 B .1.5 个小时
C .2 个小时 D .2.5 个小时
B
7 .坐在行驶的公共汽车上的小李同学,想知道汽车通过隧道所用的时间,在进出隧道时,分别看了一下手表,如图甲、乙所示.则小李同学是在 点 分进入随道的,通过 隧道共用了 分钟.小李同学出隧道时的手表示数在物理学中叫 (选填“时 间”或“时刻”).
1
20
5
时刻
A .两只摆的周期相同
B .两只摆的周期不相同
C ..左边摆的周期大于右边摆的周期
D .左边摆的周期小于右边摆的周期
8 .如图所示,是两个完全一样的摆,只是它们的摆幅不同,结果 ( )
A
课堂小结
感谢观看
THANK YOU FOR WATCHING
沪科版(五·四学制) 八年级上册
第1章 测量
1.2 时间的测量
如图 1-2-1 所示, 地铁站台显示屏上的信息预告了地铁到站的时间,方便乘客安排行程。 随着信息技术的发展,人们获知时间的方式变得越来越便捷。用刻度尺可以测量长度,用什么工具来测量时间呢?
情景引入
01
02
03
04
05
CONTENTS
图表法、数轴记录时间
古代测量时间 摆的等时性
时间的单位与换算
时间的测量
PART ONE
古代测量时间 摆的等时性
“日月忽其不淹兮,春与秋其代序。”古人观察大自然,发现白昼黑夜、四季冷暖会周而复始 地出现。以太阳连续两次出现在天空同一位置所用的时间为“日”;根据月亮的盈亏变化、四季的更替,有了“月”和“年”,这才确定了“日” “月”“年”这些时间单位。各种连续的、具有周期性的现象都可以用来测量时间。
“时”和“刻”是比年、月、日更小的时间单位。如图 1-2-3 所示, 为了满足生产、生活的需要,古人发明了日晷、漏刻等工具来测量时间。日晷利用一天中不同时刻晷针影子的位置变将晷面划分为十二时辰。
一炷香的时间
沙漏
思考:古人还有哪些测量时间的方式?
图 1-2-2 中的现象是否可以用来测量时间?
想一想
主要贡献:
发现摆的等时性
与培根提出科学实验方法
提出相对性原理
发明望远镜(伽利略望远镜)
发明最早的温度计
美誉:
现代观测天文学之父
现代物理学之父
科学之父
现代科学之父
1583 年,意大利物理学家伽利略(G. Galilei, 1564— 1642)发现同一吊灯完成一次摆动的时间大致相同。以此为基础,荷兰物理学家惠更斯 ( C. Huygens , 1629— 1695)发明了摆钟, 摆钟经不断改进沿用至今。
01.发现问题,提出假设
事情发生在400多年前的意大利比萨,年轻的伽利略当时在比萨大学学习。有一天,伽利略在教堂里发现穹顶上挂的吊灯不停地来回摆动,这本是司空见惯的现象却引起了伽利略的注意。他发现尽管吊灯摆动的幅度越来越小,但每摆动一次的时间似乎是相等的。这个现象令他大为惊奇,于是他决定仔细地观察。
提出假设:单摆的周期可能与摆球的质量、摆线的长度、摆动幅度有关。
02.设计实验
1.实验目的:探究单摆的周期与哪些因素有关
2.实验器材:不同质量(100克和200克)的摆球、不同长度(80厘米和40厘米)的摆线
3.实验步骤:
①探究单摆的周期是否与摆球的质量有关
(取长度相同的摆线,质量不同的摆球,在与竖直方向夹角相同处释放,测量摆动周期)
②探究单摆的周期是否与摆线的长度有关
(取长度不同的摆线,质量相同的摆球,在与竖直方向夹角相同处释放,测量摆动周期)
③探究单摆的周期是否与摆动幅度有关
(取长度相同的摆线,质量相同的摆球,在与竖直方向夹角不同处释放,测量摆动周期)
03.进行实验
实验序号 摆球质量(克) 摆线长度(厘米) 摆动幅度 摆动周期(秒)
1 100 80 10°
2 100 80 5°
3 100 40 5°
4 200 80 5°
由于摆动周期太小,用秒表无法精确测出!!!
?
累积法
03.进行实验
实验序号 摆球质量(克) 摆线长度(厘米) 摆动幅度 连续摆动10次的时间(秒) 摆动周期(秒)
1 100 80 10° 17.8 1.78
2 100 80 5° 17.8 1.78
3 100 40 5° 8.9 0.89
4 200 80 5° 17.8 1.78
04.归纳得到结论
实验序号 摆球质量(克) 摆线长度(厘米) 摆动幅度 连续摆动10次的时间(秒) 摆动周期(秒)
1 100 80 10° 17.8 1.78
4 200 80 5° 17.8 1.78
摆动周期与摆球质量的关系
分析实验序号1和4,可以得到的结论是:
________________________________________________________________________________
当摆线长度、摆动幅度相同时,摆动周期与摆球质量无关
条件+结论
摆动周期与摆线长度的关系
分析实验序号2和3,可以得到的结论是:
________________________________________________________________________________
当摆球质量、摆动幅度相同时,摆动周期与摆线长度有关
实验序号 摆球质量(克) 摆线长度(厘米) 摆动幅度 连续摆动10次的时间(秒) 摆动周期(秒)
2 100 80 5° 17.8 1.78
3 100 40 5° 8.9 0.89
←正确但不完整
摆线长度越长,摆动周期越长
04.归纳得到结论
摆动周期与摆动幅度的关系
分析实验序号1和2,可以得到的结论是:
________________________________________________________________________________
当摆球质量、摆线长度相同时,摆动周期与摆动幅度无关
实验序号 摆球质量(克) 摆线长度(厘米) 摆动幅度 连续摆动10次的时间(秒) 摆动周期(秒)
1 100 80 10° 17.8 1.78
2 100 80 5° 17.8 1.78
04.归纳得到结论
摆动周期只与_______________________有关
摆线长度
因此,图 1-2-2 中的荡秋千、摩天轮是可以用来测量时间的。
PART TWO
时间的单位与换算 时间的测量
在物理学中, 时间用字母t 表示。在国际单位制中, 时间的基本单位是秒( second),符号是s。人们曾根据地球自转等天文现象来确定 1 s 的长短。目前以铯原子的振动为基准来确定1 s 的长短。铯原子钟非常稳定,几千万年才相差 1 s。
比秒大的单位有分(min)、时(h), 比秒小的单位有毫秒( ms )和微秒(μs),它们与秒之间的换算关系如下:
1 h = 3 600 s
1 min = 60 s
1 ms = 10-3 s
1 μs = 10-6 s
现代测量时间工具:机械钟表、石英钟、秒表等
我们通常用时钟、手表和秒表等工具来测量时间。时钟的最小单位是分, 手表的最小单位一般是秒,使用电子秒表计时最小单 位可以到百分之一秒。记录短跑成绩时,就会用到比时钟、手表更精确的秒表。
石英钟
秒表
机械停表
电子手表
(1)量程和分度值:机械停表的外圈(大表盘)以秒为单位,内圈(小表盘)以分为单位,不同停表量程和分度值会不同,量程以小圈为准。如图中小表盘转一圈量程为60 min,外圈分度值为0.2 s。
机械停表的使用
(2)测量方法:
01
调零:使用前若指针未与零刻度线对齐,则根据停表的实际结构按动“复位”按钮进行归零
02
启动:先上好发条,用手握住停表,大拇指按下“开始/停止”按钮,开始计时
03
停止:再次按下“开始/停止”按钮,停表指针停止走动,结束计时
04
读数
(3)读数:在读数时,先读出小表盘上指针所通过的分钟数(按整数读);再观察小表盘上的指针有没有超过两数字之间的半分钟刻度线,若不超过,则大表盘按照0~30s读数,若超过,则大表盘按照31~60s读数。左图读数是5分钟37.5秒。换成秒是:337.5秒
如图,秒表的读数是 s。
活动探究
课代表分发秒表、多功能电子表,分小组操作练习。
活动:连续击掌10次,同学们用秒表和多功能电子表同时计时测量。
随讲随练
275.2
观察电子秒表
1. 观察实验室提供的电子秒表,它的最小单位是什么?
2. 电子秒表的“启动”“暂停”和“归零”按钮在哪里?
学习使用电子秒表
在计时模式下,按下“启动”按钮,电子秒表开始计时。按下“暂停”按 钮, 电子秒表停止计时,屏幕上会显示记录的时间。按下“归零”按钮后电子秒表显示的时间会重置为零。大部分电子秒表有分段计时功能,不仅可以将整 个计时过程分解,还可以递加计时。
用电子秒表测量时间
用电子秒表测量脉搏跳动 30 次的时间
测量脉搏跳动 30 次所用的时间,将测量结果填入表 1-2-1 中。
序号 脉搏跳动 30 次所用的时间 /s
1
2
3
脉搏跳动 30 次所用时间的平均值: s
交流讨论
由上述测量结果能否知道脉搏跳动一次的时间?
为什么不用电子秒表直接测量脉搏跳动一次的时间?
PART THREE
图表法、数轴记录时间
图1-2-5 是苹果下落过程中依次经过位置A 、B 、C、D 、E、F 的照片, 它是每隔0.1 s 拍摄一次而得。表1-2-2 记录了苹果从图中位置 A 到其他各个位置所用的时间。
位置 A B C D E F
运动时间 /s 0 0.1 0.2 0.3 0.4 0.5
表 1-2-2 数据记录表
我们也可以把苹果下落的时间信息记录在数轴上。图1-2-6 中的tAD 表示苹果从位置 A 下落 到位置 D 所用的时间,线段 AD 的长度可以直观地表示tAD 的长短。
1.每周一庄严的升旗礼上,我们要唱国歌、行注目礼。此环节国歌演奏的时长约为 ( )
A . 0.5s B .5s
C .50s D . 5min
课堂练习
C
2 .下列过程中,经历的时间差不多为 1 秒的是 ( )
A .人的眼睛眨一下的时间
B .人呼吸一次的时间
C .人的心脏跳动一次的时间
D .人行走 5 米路程所需的时间
C
日晷
卷尺
3 .下列工具不能用来计时的是 ( )
A .
C .
B .
D .
电子手表
沙漏
C
4 .如图,停表的读数为 s。
220.5
5 .为了研究单摆摆动的周期与摆线长度的关系,应保持 ( )
A .摆线的长度和摆球的质量不变,改变摆动的幅度
B .摆线的长度和摆动的幅度不变,改变摆球的质量
C .摆动的幅度和摆球的质量不变,改变摆线的长度
D .摆动的幅度和摆球的质量,摆线的长度都不变,改变摆球的形状
C
6 .周末上午李妍同学在开始写作业时看了一下表,表的指针如图甲所示;李妍写完作业之后又看了一次表,此时表的指针如图乙所示(时间都是上午),则李妍写作业所用的时间为( )
A .1 个小时 B .1.5 个小时
C .2 个小时 D .2.5 个小时
B
7 .坐在行驶的公共汽车上的小李同学,想知道汽车通过隧道所用的时间,在进出隧道时,分别看了一下手表,如图甲、乙所示.则小李同学是在 点 分进入随道的,通过 隧道共用了 分钟.小李同学出隧道时的手表示数在物理学中叫 (选填“时 间”或“时刻”).
1
20
5
时刻
A .两只摆的周期相同
B .两只摆的周期不相同
C ..左边摆的周期大于右边摆的周期
D .左边摆的周期小于右边摆的周期
8 .如图所示,是两个完全一样的摆,只是它们的摆幅不同,结果 ( )
A
课堂小结
感谢观看
THANK YOU FOR WATCHING
同课章节目录
