湘教版八年级数学下册课件:4.3.2 一次函数的图象和性质(共15张PPT)
文档属性
| 名称 | 湘教版八年级数学下册课件:4.3.2 一次函数的图象和性质(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 122.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-28 00:00:00 | ||
图片预览





文档简介
课件15张PPT。11/23/2018 既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗? 它们图象之间有什么关系?一次函数又有什么性质呢?创设问题11/23/2018一次函数的图象及性质11/23/2018......1、请大家用描点法在同一坐标系内画出一次函数y=x+2,y=x-2的图象。合作探索0-31-42-23-140....y=x+2y=x-22、观察与比较::
观察它们的图象有什么特点?
结论:一次函数的图象是一条直线,即函数y=kx+b(k≠0)的图象叫直线y=kx+b
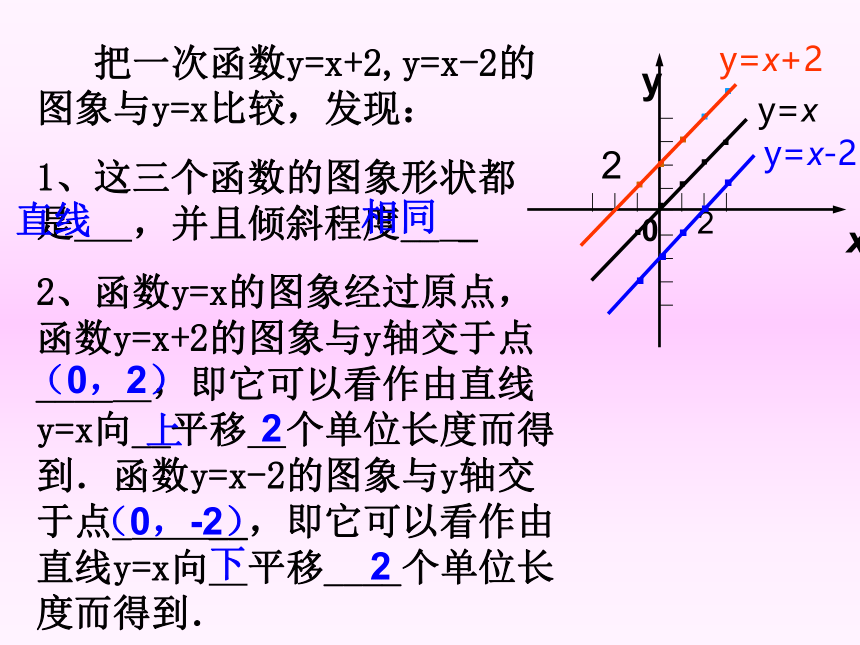
11/23/2018 把一次函数y=x+2,y=x-2的图象与y=x比较,发现:
1、这三个函数的图象形状都是 ,并且倾斜程度__ _
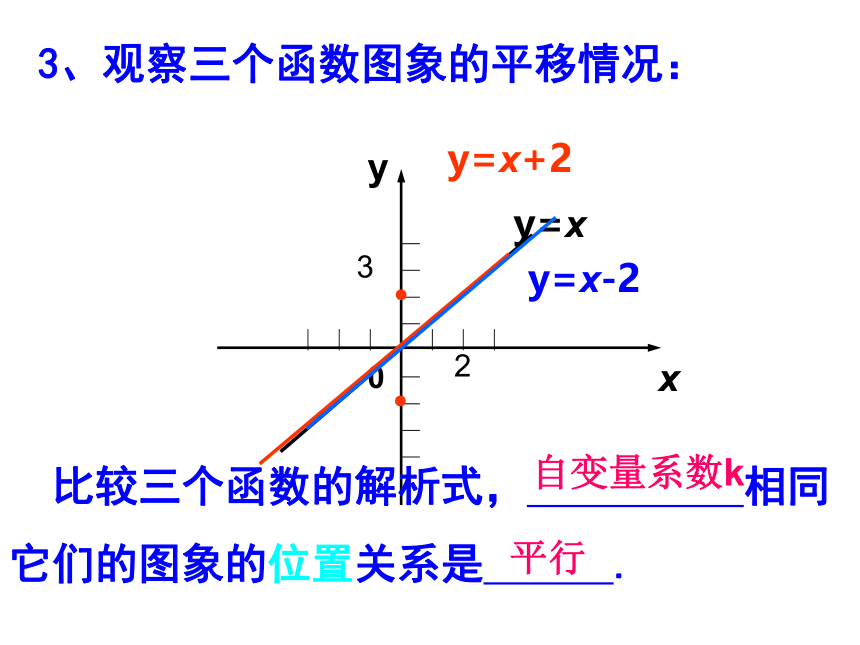
2、函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点____ ,即它可以看作由直线y=x向__平移 个单位长度而得到.函数y=x-2的图象与y轴交于点_ __,即它可以看作由直线y=x向 平移____个单位长度而得到.直线相同(0,2)上2(0,-2)下2211/23/2018y=xy=x+2y=x-2y30●● 比较三个函数的解析式, 相同
它们的图象的位置关系是 . 自变量系数k平行3、观察三个函数图象的平移情况:11/23/20184、你能说出一次函数y=-x-1与y=-x+1 的
图象是由直线y=-x怎样平移得到的吗? 你能猜想一次函数y=kx+b的图象与正
比例函数y=kx图象有什么关系吗?11/23/2018课堂练习1:(1)直线y=-6x+5可由直线y=-6x
向 平移 单位得到。(2)直线a1; y=-2x-1, 直线a2 : y=-2x, 直线a3 : y=-2x+1的位置关系是 。上5平行(3)直线y=kx-4与直线y=-2x平行,
则k= 。 -2(4) 函数y=2x- 4的图象与y轴的交点坐标
为 与x轴的交点为 。 (0,-4)(2,0)直线y=kx+b(k≠0)与y轴的交点为(0,b),与
x轴的交点为 ( ,0), 11/23/2018例1画出函数y=2x-1与 的图象.yxo11····y=2x-1-112-1解:0002由于一次函数的图象是直线,所以只要确定两个合适的点就能画出它。11/23/2018在同一直角坐标系中画出函数 的图象
(1)y=x+l与 y=2x+1 ,
(2)y=-2x+l与y=-x+1
观察:k的正负对函数图象有什么 影响?合作探究2:11/23/2018y=x+ly=2x+l●●●Oyxy=-x+ly=-2x+l结论:当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小 。11/23/2018例 题例2、对于一次函数y=(3m+6)x+m-4,求
(1)m为何值时,y随x的增大而减小?
(2) m为何值时,该直线经过原点?
(3) m为何值,该直线与y轴的交点在x轴的下方?解:(1)因为y随x的增大而减小,
所以 3m+6 <0 即 m<-2(2)由题意得: 3m+6≠0且m-4=0
解得:m=4(3)由题意得: 3m+6≠0且m-4<0
解得:m<4且m ≠-211/23/20182、对于函数y=mx-3,y随x增大而减小,则该直线经过
象限 。 1、有下列函数:①y=2x+1, ②y= -3x+4,③y=0.5x,④y=x-6; ①③ ④②③函数y随x的增大而增大的是_____ ____ __;其中过原点的直线是________;函数y随x的增大而减小的是___________;课堂练习:2第 二、三、四11/23/20183、一次函数y=(4m+1)x-(m+1)
(1)当m 时,y随x的增大而增大。
(2)当m 时,直线与y轴的交点在x轴的下方。相对于一次函数y=kx+b(k≠0),这里的k、b分别代表什么式子?11/23/20184、一次函数y=kx+b中,kb>0,且y随x的增大
而减小,则它的图象大致为( )Cxxxxyyyyoooo11/23/2018课堂小结2、会画一次函数的图象3、一次函数的图象与性质,常数k,b的意义和作用1、一次函数的图象是一条直线
观察它们的图象有什么特点?
结论:一次函数的图象是一条直线,即函数y=kx+b(k≠0)的图象叫直线y=kx+b
11/23/2018 把一次函数y=x+2,y=x-2的图象与y=x比较,发现:
1、这三个函数的图象形状都是 ,并且倾斜程度__ _
2、函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点____ ,即它可以看作由直线y=x向__平移 个单位长度而得到.函数y=x-2的图象与y轴交于点_ __,即它可以看作由直线y=x向 平移____个单位长度而得到.直线相同(0,2)上2(0,-2)下2211/23/2018y=xy=x+2y=x-2y30●● 比较三个函数的解析式, 相同
它们的图象的位置关系是 . 自变量系数k平行3、观察三个函数图象的平移情况:11/23/20184、你能说出一次函数y=-x-1与y=-x+1 的
图象是由直线y=-x怎样平移得到的吗? 你能猜想一次函数y=kx+b的图象与正
比例函数y=kx图象有什么关系吗?11/23/2018课堂练习1:(1)直线y=-6x+5可由直线y=-6x
向 平移 单位得到。(2)直线a1; y=-2x-1, 直线a2 : y=-2x, 直线a3 : y=-2x+1的位置关系是 。上5平行(3)直线y=kx-4与直线y=-2x平行,
则k= 。 -2(4) 函数y=2x- 4的图象与y轴的交点坐标
为 与x轴的交点为 。 (0,-4)(2,0)直线y=kx+b(k≠0)与y轴的交点为(0,b),与
x轴的交点为 ( ,0), 11/23/2018例1画出函数y=2x-1与 的图象.yxo11····y=2x-1-112-1解:0002由于一次函数的图象是直线,所以只要确定两个合适的点就能画出它。11/23/2018在同一直角坐标系中画出函数 的图象
(1)y=x+l与 y=2x+1 ,
(2)y=-2x+l与y=-x+1
观察:k的正负对函数图象有什么 影响?合作探究2:11/23/2018y=x+ly=2x+l●●●Oyxy=-x+ly=-2x+l结论:当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小 。11/23/2018例 题例2、对于一次函数y=(3m+6)x+m-4,求
(1)m为何值时,y随x的增大而减小?
(2) m为何值时,该直线经过原点?
(3) m为何值,该直线与y轴的交点在x轴的下方?解:(1)因为y随x的增大而减小,
所以 3m+6 <0 即 m<-2(2)由题意得: 3m+6≠0且m-4=0
解得:m=4(3)由题意得: 3m+6≠0且m-4<0
解得:m<4且m ≠-211/23/20182、对于函数y=mx-3,y随x增大而减小,则该直线经过
象限 。 1、有下列函数:①y=2x+1, ②y= -3x+4,③y=0.5x,④y=x-6; ①③ ④②③函数y随x的增大而增大的是_____ ____ __;其中过原点的直线是________;函数y随x的增大而减小的是___________;课堂练习:2第 二、三、四11/23/20183、一次函数y=(4m+1)x-(m+1)
(1)当m 时,y随x的增大而增大。
(2)当m 时,直线与y轴的交点在x轴的下方。相对于一次函数y=kx+b(k≠0),这里的k、b分别代表什么式子?11/23/20184、一次函数y=kx+b中,kb>0,且y随x的增大
而减小,则它的图象大致为( )Cxxxxyyyyoooo11/23/2018课堂小结2、会画一次函数的图象3、一次函数的图象与性质,常数k,b的意义和作用1、一次函数的图象是一条直线
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
