新课标人教A版数学:证明数列不等式之放缩技巧
文档属性
| 名称 | 新课标人教A版数学:证明数列不等式之放缩技巧 |

|
|
| 格式 | zip | ||
| 文件大小 | 147.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-02 00:00:00 | ||
图片预览


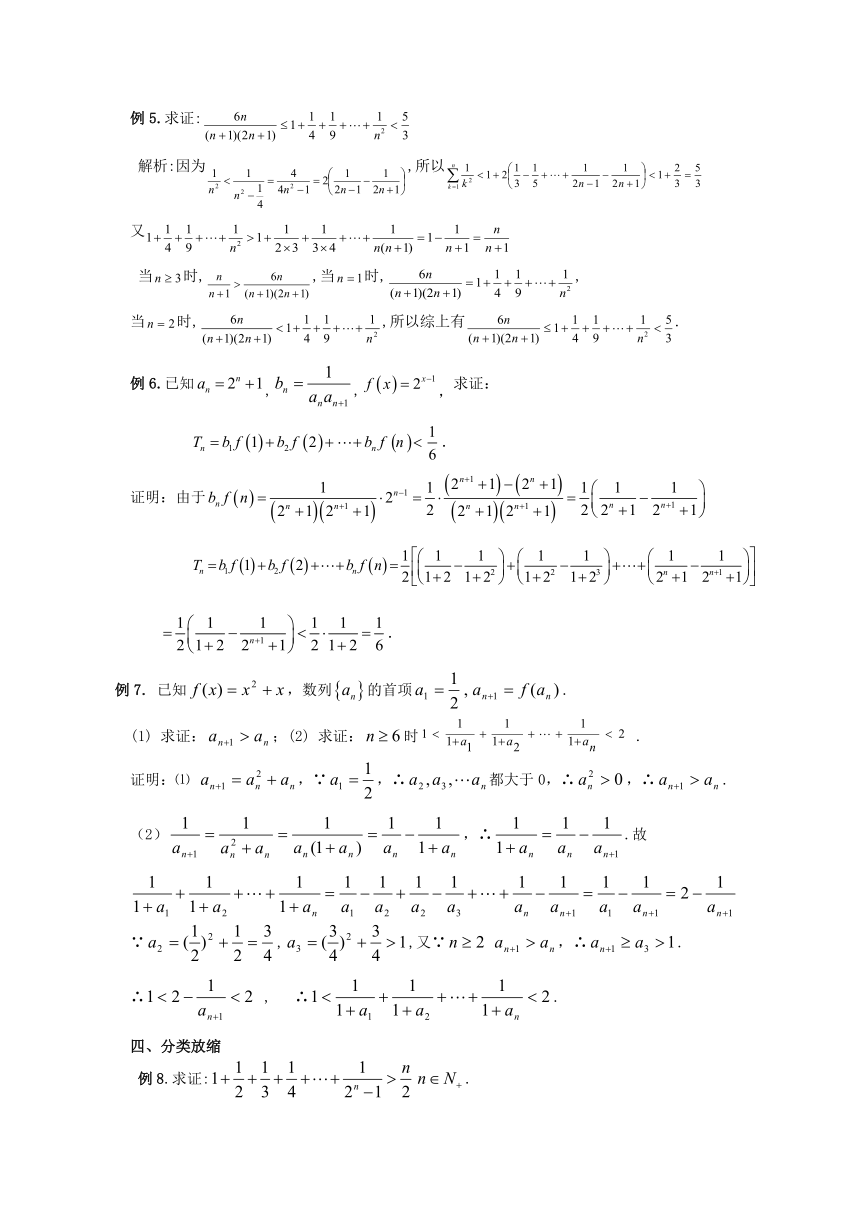
文档简介
证明数列不等式之放缩技巧
证明数列型不等式,其思维跨度大、构造性强 ( http: / / www.21cnjy.com ),需要有较高的放缩技巧,充满思考性和挑战性。这类问题的求解策略往往是:通过多角度观察所给数列通项的结构,深入剖析其特征,抓住其规律进行恰当地放缩.
一、利用数列的单调性
例1.证明:当时,.
证法一:令,则,
所以当时,.因此当时,
于是当时,
证法二:可用数学归纳法证.(1)当n = 6时,成立.
(2)假设当时不等式成立,即
则当n=k+1时,
由(1)、(2)所述,当n≥6时,.
二、借助数列递推关系
例2.已知.证明:.
证明:,
∴.
例3. 已知函数f(x)=,设正项数列满足=l,.
(1) 试比较与的大小,并说明理由;
(2) 设数列满足=-,记Sn=.证明:当n≥2时,Sn<(2n-1).
分析:比较大小常用的办法是作差法,而求和式的不等式常用的办法是放缩法。
解:(1) 因为所以
,因为所以与同号,因为,…,即
(2)当时,,
所以,
所以.
例4. 已知不等式其中为不大于2的整数,表示不超过的最大整数。设数列的各项为正且满足.证明:,.
证明:由得:,
, ,… ,,
以上各式两边分别相加得:,
=,
.
裂项放缩
例5.求证:
解析:因为,所以
又
当时,,当时,,
当时,,所以综上有.
例6.已知,,,求证:
.
证明:由于
.
例7. 已知,数列的首项.
求证:;(2) 求证:时.
证明:⑴ ,∵,∴都大于0,∴,∴.
,∴.故
∵,,又∵,∴.
∴ , ∴.
四、分类放缩
例8.求证:.
证明:当时不等式显然成立.
.
例9. 已知.证明:对任意整数,有.
分析:不等式左边很复杂,要设法对左边的项进行适当放缩,使之能够求和。
而左边=,如果我们把上式中的分母中的去掉,就可利用等比数列的前n项公式求和,由于-1与1交错出现,容易想到将式中两项两项地合并起来一起进行放缩,尝试知:,,因此,可将保留,再将后面的项两两组合后放缩,即可求和。这里需要对进行分类讨论,(1)当为偶数时,
(2)当是奇数时,为偶数,
.
所以对任意整数,有。
五、利用函数单调性(导数)放缩
例10. 已知函数,数列满足, ; 数列
满足, .求证:
(Ⅰ)(Ⅱ) (Ⅲ)若则当n≥2时,.
分析:第(1)问用数学归纳法证明;第(2)问利用函数的单调性;第(3)问进行放缩。
证明:(Ⅰ)先用数学归纳法证明,.
(1)当n=1时,由已知得结论成立;
(2)假设当n=k时,结论成立,即.则当n=k+1时,
因为0又f(x)在上连续,所以f(0)故当n=k+1时,结论也成立. 即对于一切正整数都成立.
又由, 得,从而.
综上可知
(Ⅱ)构造函数g(x)=-f(x)= , 0由,知g(x)在(0,1)上增函数. 又g(x)在上连续,所以g(x)>g(0)=0.
因为,所以,即>0,从而
(Ⅲ) 因为 ,所以, ,
所以 ————①
由(Ⅱ)知:, 所以= ,
因为, n≥2,
所以 <<=————②
由①② 两式可知: .
例11.求证:.
证明:先构造函数有,从而
因为
所以
证明数列型不等式,其思维跨度大、构造性强 ( http: / / www.21cnjy.com ),需要有较高的放缩技巧,充满思考性和挑战性。这类问题的求解策略往往是:通过多角度观察所给数列通项的结构,深入剖析其特征,抓住其规律进行恰当地放缩.
一、利用数列的单调性
例1.证明:当时,.
证法一:令,则,
所以当时,.因此当时,
于是当时,
证法二:可用数学归纳法证.(1)当n = 6时,成立.
(2)假设当时不等式成立,即
则当n=k+1时,
由(1)、(2)所述,当n≥6时,.
二、借助数列递推关系
例2.已知.证明:.
证明:,
∴.
例3. 已知函数f(x)=,设正项数列满足=l,.
(1) 试比较与的大小,并说明理由;
(2) 设数列满足=-,记Sn=.证明:当n≥2时,Sn<(2n-1).
分析:比较大小常用的办法是作差法,而求和式的不等式常用的办法是放缩法。
解:(1) 因为所以
,因为所以与同号,因为,…,即
(2)当时,,
所以,
所以.
例4. 已知不等式其中为不大于2的整数,表示不超过的最大整数。设数列的各项为正且满足.证明:,.
证明:由得:,
, ,… ,,
以上各式两边分别相加得:,
=,
.
裂项放缩
例5.求证:
解析:因为,所以
又
当时,,当时,,
当时,,所以综上有.
例6.已知,,,求证:
.
证明:由于
.
例7. 已知,数列的首项.
求证:;(2) 求证:时.
证明:⑴ ,∵,∴都大于0,∴,∴.
,∴.故
∵,,又∵,∴.
∴ , ∴.
四、分类放缩
例8.求证:.
证明:当时不等式显然成立.
.
例9. 已知.证明:对任意整数,有.
分析:不等式左边很复杂,要设法对左边的项进行适当放缩,使之能够求和。
而左边=,如果我们把上式中的分母中的去掉,就可利用等比数列的前n项公式求和,由于-1与1交错出现,容易想到将式中两项两项地合并起来一起进行放缩,尝试知:,,因此,可将保留,再将后面的项两两组合后放缩,即可求和。这里需要对进行分类讨论,(1)当为偶数时,
(2)当是奇数时,为偶数,
.
所以对任意整数,有。
五、利用函数单调性(导数)放缩
例10. 已知函数,数列满足, ; 数列
满足, .求证:
(Ⅰ)(Ⅱ) (Ⅲ)若则当n≥2时,.
分析:第(1)问用数学归纳法证明;第(2)问利用函数的单调性;第(3)问进行放缩。
证明:(Ⅰ)先用数学归纳法证明,.
(1)当n=1时,由已知得结论成立;
(2)假设当n=k时,结论成立,即.则当n=k+1时,
因为0
又由, 得,从而.
综上可知
(Ⅱ)构造函数g(x)=-f(x)= , 0
因为,所以,即>0,从而
(Ⅲ) 因为 ,所以, ,
所以 ————①
由(Ⅱ)知:, 所以= ,
因为, n≥2,
所以 <<=————②
由①② 两式可知: .
例11.求证:.
证明:先构造函数有,从而
因为
所以
