21.2.4 一元二次方程的根与系数的关系 课件 (共20张PPT) 2024-205学年数学人教版九年级上册
文档属性
| 名称 | 21.2.4 一元二次方程的根与系数的关系 课件 (共20张PPT) 2024-205学年数学人教版九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-18 19:18:39 | ||
图片预览







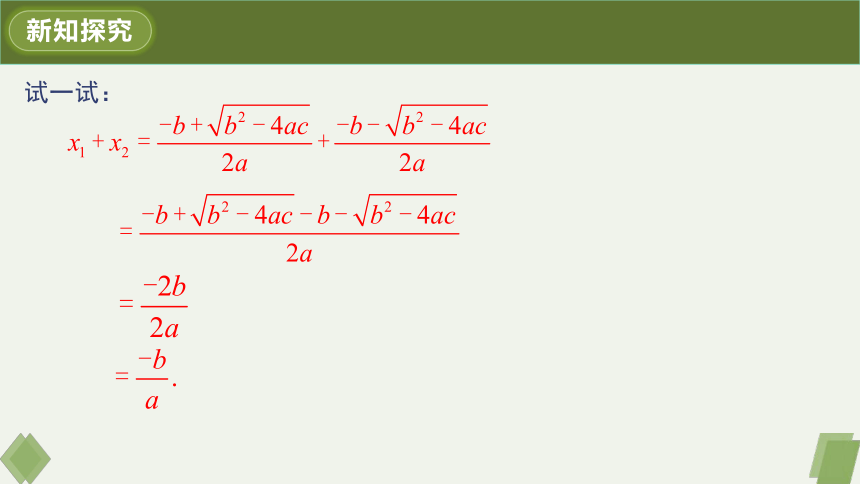
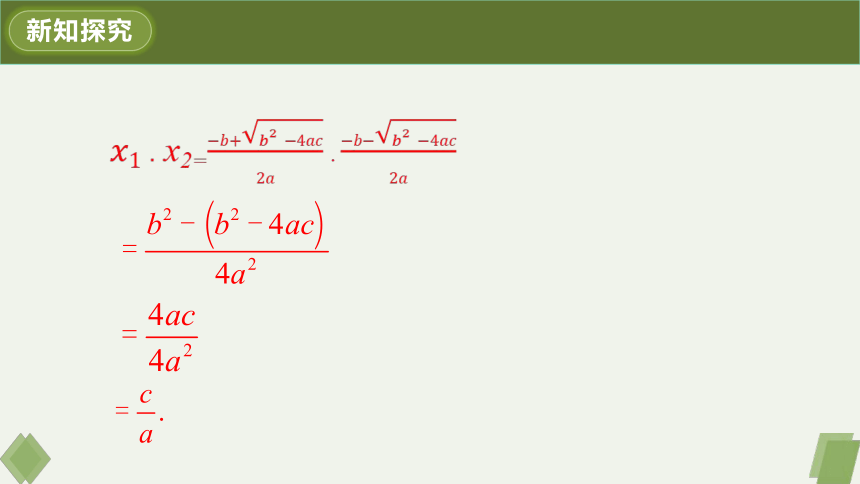
文档简介
(共20张PPT)
第21章
一元二次方程
21.2.4一元二次方程的根与系数的关系
教学目标/Teaching aims
1
熟练掌握一元二次方程的根与系数的关系;
3
经历探索一元二次方程的根与系数的关系,发展学生的逻辑推理和数学运算的核心素养,培养学生观察、分析、归纳和判断的能力;
2
灵活运用一元二次方程的根与系数的关系解决实际问题;
情景导入
法国数学家弗朗索瓦·韦达于1615年在《论方程的识别与订正》一书中建立了方程根与系数的关系.今天我们就跟随数学家韦达的脚步一起来探究一下:一元二次方程的根与系数的关系.
复习回顾
大家知道方程的求根公式 不仅表示可以由方程的系数a,b,c决定根的值,而且反映了根与系数之间的联系.那么,一元二次方程根与系数之间的联系还有其他的表示方式吗?
新知探究
(x-x1)(x-x2)=0.
由因式分解法可得:
x-x1=0
或
x-x2=0
x=x1
则:
x=x2
或
方程:
将方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗?
新知探究
(x-x1)(x-x2)=0.
x2-(x1+x2)x+x1·x2=0,
x2 + px+ q=0,
x1+x2= -p
x1 ·x2=q.
两根之和
两根之积
与系数的关系
新知探究
一般的一元二次方程ax2+bx+c=0中,二次项系数a未必是1,它的两个根的和、积与系数又有怎样的关系呢?
新知探究
试一试:
新知探究
x2=
归纳小结
根与系数的关系:
方程的两个根x1,x2和系数a,b,c有如下关系:
满足上述关系的前提条件
b2-4ac≥0.
巩固练习
2
1
8
-12
巩固练习
D
2
8
新知探究
巩固练习
1.已知a,b是方程 2x2-3x-5=0的两个根,不解方程,求下列代数式的值:
(1)|a-b|; (2)(1-a)(1-b).
课堂练习
1.已知方程 2-5x=x2 的两个实数根分别为 x1,x2,则 x1x2 的值为 ( )
A.5 B.-5
C.2 D.-2
D
课堂练习
2.若关于x的方程 x2-4x+m=0 有一个根为-1,则另一个根为
( )
A.-2 B.2
C.-5 D.5
3.如果 x1,x2是一元二次方程 2x2-kx+1-k=0 的两个实数根,且 x1+x2=3,那么 k=_________.
D
6
课堂练习
4.已知关于 x 的一元二次方程 x2+5x-p2=0 的两个实数根为 x1,x2,当 x1+x2=x1x2 时,求 p 的值.
课堂练习
5.已知 m,n分别为一元二次方程 x2+2x-2 021=0 的两个实数根,则 m2+3m+n=_________.
2 019
课堂总结
根与系数的关系(韦达定理)
内容
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
应用
21.2.4一元二次方程的根与系数的关系
谢谢观看
一元二次方程
第21章
一元二次方程
21.2.4一元二次方程的根与系数的关系
教学目标/Teaching aims
1
熟练掌握一元二次方程的根与系数的关系;
3
经历探索一元二次方程的根与系数的关系,发展学生的逻辑推理和数学运算的核心素养,培养学生观察、分析、归纳和判断的能力;
2
灵活运用一元二次方程的根与系数的关系解决实际问题;
情景导入
法国数学家弗朗索瓦·韦达于1615年在《论方程的识别与订正》一书中建立了方程根与系数的关系.今天我们就跟随数学家韦达的脚步一起来探究一下:一元二次方程的根与系数的关系.
复习回顾
大家知道方程的求根公式 不仅表示可以由方程的系数a,b,c决定根的值,而且反映了根与系数之间的联系.那么,一元二次方程根与系数之间的联系还有其他的表示方式吗?
新知探究
(x-x1)(x-x2)=0.
由因式分解法可得:
x-x1=0
或
x-x2=0
x=x1
则:
x=x2
或
方程:
将方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗?
新知探究
(x-x1)(x-x2)=0.
x2-(x1+x2)x+x1·x2=0,
x2 + px+ q=0,
x1+x2= -p
x1 ·x2=q.
两根之和
两根之积
与系数的关系
新知探究
一般的一元二次方程ax2+bx+c=0中,二次项系数a未必是1,它的两个根的和、积与系数又有怎样的关系呢?
新知探究
试一试:
新知探究
x2=
归纳小结
根与系数的关系:
方程的两个根x1,x2和系数a,b,c有如下关系:
满足上述关系的前提条件
b2-4ac≥0.
巩固练习
2
1
8
-12
巩固练习
D
2
8
新知探究
巩固练习
1.已知a,b是方程 2x2-3x-5=0的两个根,不解方程,求下列代数式的值:
(1)|a-b|; (2)(1-a)(1-b).
课堂练习
1.已知方程 2-5x=x2 的两个实数根分别为 x1,x2,则 x1x2 的值为 ( )
A.5 B.-5
C.2 D.-2
D
课堂练习
2.若关于x的方程 x2-4x+m=0 有一个根为-1,则另一个根为
( )
A.-2 B.2
C.-5 D.5
3.如果 x1,x2是一元二次方程 2x2-kx+1-k=0 的两个实数根,且 x1+x2=3,那么 k=_________.
D
6
课堂练习
4.已知关于 x 的一元二次方程 x2+5x-p2=0 的两个实数根为 x1,x2,当 x1+x2=x1x2 时,求 p 的值.
课堂练习
5.已知 m,n分别为一元二次方程 x2+2x-2 021=0 的两个实数根,则 m2+3m+n=_________.
2 019
课堂总结
根与系数的关系(韦达定理)
内容
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
应用
21.2.4一元二次方程的根与系数的关系
谢谢观看
一元二次方程
同课章节目录
