6.4 生活中的圆周运动 课件(共31张PPT)高中物理人教版(2019)必修 第二册
文档属性
| 名称 | 6.4 生活中的圆周运动 课件(共31张PPT)高中物理人教版(2019)必修 第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 38.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-20 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
6.4 生活中的圆周运动
第六章 圆周运动
人教版(2019)必修 第二册
1. 能根据所学知识分析生活中的各种圆周运动现象,在此过程中体会模型建构的方法。
2.知道航天器中的失重现象。
3.观察生活中的离心现象,知道离心运动产生的原因,了解其在生活中的应用,并知道离心运动带来的危害。
学习目标
提供物体做圆周运动的力,由物体受力情况决定。
做圆周运动的物体所需的力,由物体的运动情况决定。
F供=F需时,物体做圆周运动
复习
牛顿第二定律F合=ma的应用
导入新课
在铁路弯道处,内、外轨道的高度略有不同,你能解释其中的原因吗?
讨论
火车为什么会发生脱轨事故呢?
新课入
一、火车转弯
讨论
铁轨
踏面
轮缘
火车车轮
G
N
.
F
外轨
内轨
思考1: 火车转弯时可看做匀速圆周运动,如果火车内外轨道一样高,向心力主要来源是什么?
由外侧轨道对车轮轮缘的挤压力提供。
分析:火车质量太大,靠这种办法得到向心力,轮缘与外轨间的相互作用力太大,铁轨和车轮极易受损。
结论:
靠这种办法得到的向心力弊端是什么?
讨论
内侧轨道
外侧轨道
水平线
火车在转弯时,轨迹为水平面内一段圆弧。
外轨略高于内轨。
火车转弯的轨道
θ
问题:
圆周面在哪里?
圆心在哪里?
向心加速度方向在哪里?
FN
h
F合
思考2:如图,斜面轨道倾角为θ,转弯半径r,要使车轮轮沿对内外轨都无压力,质量为m的火车运行的速率应该多大
G
O
r
分析:
火车拐弯应以设计速度行驶
火车转弯设计速度:
由 得,
θ
当火车行驶速率v实际>v设计时
当火车行驶速率v实际G
FN
G
FN
FN′
外轨对轮缘有侧压力
内轨对轮缘有侧压力
讨论
FN′
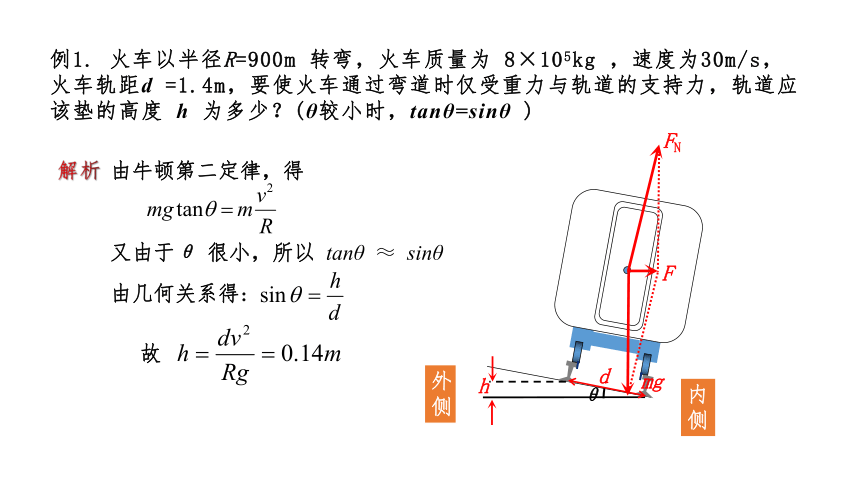
例1. 火车以半径R=900m 转弯,火车质量为 8×105kg ,速度为30m/s,火车轨距d =1.4m,要使火车通过弯道时仅受重力与轨道的支持力,轨道应该垫的高度 h 为多少?(θ较小时,tanθ=sinθ )
θ
h
d
外
侧
内侧
FN
mg
F
由几何关系得:
又由于θ 很小,所以 tanθ ≈ sinθ
由牛顿第二定律,得
故
解析
G
F
F合
类火车转弯
1.飞机转弯
O
mg
FN
f
汽车在水平地面上转弯是什么力提供向心力的呢
讨论
2.公路弯道
动力学方程
有的公路弯道处树立限速指示牌,为什么?设车轮与水平路面间动摩擦因数为μ,汽车速度不能超过多少?
当汽车转弯的半径一定时,
分析
Ff Ffm ,汽车将侧滑。
由此可见:当汽车转弯时,存在一个安全通过的最大速度,如果超过了这个速度,汽车将发生侧滑现象。
改进措施:
(1)增大转弯半径
(2)增加路面的粗糙程度
(3)最重要的一点:司机应该减速慢行!
(4)增加路面高度差——外高内低
思考:公路上的拱形桥是常见的,汽车过桥时,也可以看做圆周运动。
为什么凸形桥比凹形桥更普遍呢?
新课入
二、汽车过拱形桥
问题1:汽车过拱形桥时,在最高点时,车对凸桥的压力怎样?
mg
FN
,即处于失重。
F压 <mg
半径r
由牛顿第三定律得,汽车通过桥的最高点时对桥的压力:
汽车通过桥最高点时的向心力由什么力提供?
由 得,
重力和支持力的合力提供向心力
解析
讨论
⑴汽车处于超重还是失重状态?
当 FN = 0 时,汽车脱离桥面,做平抛运动,
汽车及其中的物体处于完全失重状态。
⑵汽车过拱形桥时,运动速度变大,车对凸桥的压力如何变化?
mg
FN
当 时,可过;
当 时,飞出。
v=
由 得,
结论:
⑶ FN=0 时,汽车的速度为多大?
称为安全行驶最大速度
v=
实例
问题2:汽车过凹形桥时,在最低点时,车对凹桥的压力又怎样?
FN
mg
汽车对桥的压力大于其所受重力,即处于超重。
F压 >mg
由牛顿第三定律得,汽车通过桥的最低点时对桥的压力:
汽车通过桥最低点时的向心力由什么力提供?
由 得,
汽车过凹形桥时需要有速度限制吗?
思考:
重力和支持力的合力提供向心力
解析
地球可以看作一个巨大的拱形桥,桥面的半径就是地球的半径 R(约为 6 400 km)。地面上有一辆汽车在行驶,所受重力 G = mg,地面对它的支持力是 FN 。
根据上面的分析,汽车速度越大,地面对它的支持力就越小。会不会出现这样的情况:速度大到一定程度时,地面对车的支持力是 0 ?这时驾驶员与座椅之间的压力是多少?驾驶员躯体各部分之间的压力是多少?他这时可能有什么感觉?
4
新课入
三、航天器中的失重现象
讨论
汽车车速为v,地球半径为R,
汽车对桥面的压力为0
代入g=9.8m/s2,R=6371km,得
v ≈ 7900m/s
当 时,
分析
R
在绕地球做匀速圆周运动的宇宙飞船中的宇航员,除了地球引力外,还可能受到飞船座舱对他的支持力 FN :
航天员处于完全失重状态。
由 得,
当 时,座舱对他的支持力 FN = 0。
R
实例:航天器中的失重现象
做圆周运动的物体,在提供的向心力突然消失,或者不足以提供圆周运动所需的向心力的情况下,就做逐渐远离圆心的运动。
新课入
四、离心运动
1.什么叫离心运动?
2.本质
做圆周运动的物体,由于本身惯性,总有沿着圆周切线飞出去的倾向。
F合=0 或 F供 < F需
是由指向圆心的合力来充当的,可以是重力、拉力、摩擦力等;
是由物体的运动速度来决定的,即:
F需 =
“供”“需”是否平衡决定物体是否做圆周运动
F供
F需
物体作离心运动的条件:
小结:
3.物体做离心运动的条件
当 F=mω2r 时,做匀速圆周运动;
当 F=0 时,沿切线方向飞出;
当 F<mω2r 时,逐渐远离圆心;
当 F>mω2r 时,逐渐靠近圆心。
分析:
F=0
FF=mrω2
F>mrω2
3.离心运动的应用和防止
洗衣机脱水时利用离心运动把附着在物体上的水分甩掉;纺织厂也用这样的方法使棉纱、毛线、纺织品干燥。
①洗衣机脱水
②棉花糖的制作
⑴离心运动的应用
③无缝钢管
在炼钢厂中,把熔化的钢水浇入圆柱形模子,模子沿圆柱的中心轴线高速旋转。
钢水由于离心运动趋于周壁,冷却后就形成无缝钢管。
高速旋转的飞轮、砂轮的限速
对于一些本身转动的物体也要预防离心现象例如:高速转动的砂轮、飞轮等,都不得超过允许的最大转速。
转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力,离心运动会使它们破裂,酿成事故。
高速转动的砂轮
⑵离心运动的防止
D
1.如图,某公路急转弯处是一圆弧,当汽车行驶的速率为vc时,汽车恰好没有向公路内外两侧滑动的趋势。则当汽车在该弯道处 ( )
A.车速低于vc时,车辆就向内侧滑动
B.车速高于vc时,车辆就向外侧滑动
C.路面结冰时,与未结冰时相比,vc的值变小
D.路面结冰时,与未结冰时相比,vc的值不变
课堂评价
2.如图所示,铁路在弯道处的内外轨道高低是不同的,已知内外轨组成的轨道平面与水平面的夹角为θ,弯道处的圆弧半径为R,若质量为m的火车以速度v通过某弯道时,内外轨道均不受侧压力作用,下面分析正确的是 ( )
A.
B.若火车速度大于v时,火车将受到外轨侧压力作用,其方向平行轨道平面向外
C.为解决火车高速转弯时外轨受损这一难题,可以适当增大弯道半径或适当增加内外轨的高度差
D.无论火车以何种速度行驶,对内侧轨道都有压力
C
3. 有一辆质量为 800kg 的小汽车驶上圆弧半径为 50 m 的拱桥。
⑴汽车到达桥顶时速度为5m/s,汽车对桥的压力是多大?
⑵汽车以多大速度经过桥顶时恰好腾空,对桥没有压力?
⑶汽车对地面的压力过小是不安全的。从这个角度讲,汽车过桥时的速度不能过大。对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全?
⑷如果拱桥的半径增大到与地球半径R一样,汽车要在桥面上腾空,速度要多大?
1.火车转弯:v0= gR tanθ时,重力 G 和支持力 FN 的合力来提供火车转弯时所需的向心力。v>v0,外轨有挤压;v< v0,内轨有挤压。
2.拱桥: FN =mg-mv2/R凹桥:FN=mg+mv2/R>mg超重现象。
3.在所受合外力突然消失或不足以提供圆周运动所需向心力时F4.离心运动的应用:洗衣机脱水
离心运动的防止:汽车拐弯时限速。
新课入
课堂小结
6.4 生活中的圆周运动
第六章 圆周运动
人教版(2019)必修 第二册
1. 能根据所学知识分析生活中的各种圆周运动现象,在此过程中体会模型建构的方法。
2.知道航天器中的失重现象。
3.观察生活中的离心现象,知道离心运动产生的原因,了解其在生活中的应用,并知道离心运动带来的危害。
学习目标
提供物体做圆周运动的力,由物体受力情况决定。
做圆周运动的物体所需的力,由物体的运动情况决定。
F供=F需时,物体做圆周运动
复习
牛顿第二定律F合=ma的应用
导入新课
在铁路弯道处,内、外轨道的高度略有不同,你能解释其中的原因吗?
讨论
火车为什么会发生脱轨事故呢?
新课入
一、火车转弯
讨论
铁轨
踏面
轮缘
火车车轮
G
N
.
F
外轨
内轨
思考1: 火车转弯时可看做匀速圆周运动,如果火车内外轨道一样高,向心力主要来源是什么?
由外侧轨道对车轮轮缘的挤压力提供。
分析:火车质量太大,靠这种办法得到向心力,轮缘与外轨间的相互作用力太大,铁轨和车轮极易受损。
结论:
靠这种办法得到的向心力弊端是什么?
讨论
内侧轨道
外侧轨道
水平线
火车在转弯时,轨迹为水平面内一段圆弧。
外轨略高于内轨。
火车转弯的轨道
θ
问题:
圆周面在哪里?
圆心在哪里?
向心加速度方向在哪里?
FN
h
F合
思考2:如图,斜面轨道倾角为θ,转弯半径r,要使车轮轮沿对内外轨都无压力,质量为m的火车运行的速率应该多大
G
O
r
分析:
火车拐弯应以设计速度行驶
火车转弯设计速度:
由 得,
θ
当火车行驶速率v实际>v设计时
当火车行驶速率v实际
FN
G
FN
FN′
外轨对轮缘有侧压力
内轨对轮缘有侧压力
讨论
FN′
例1. 火车以半径R=900m 转弯,火车质量为 8×105kg ,速度为30m/s,火车轨距d =1.4m,要使火车通过弯道时仅受重力与轨道的支持力,轨道应该垫的高度 h 为多少?(θ较小时,tanθ=sinθ )
θ
h
d
外
侧
内侧
FN
mg
F
由几何关系得:
又由于θ 很小,所以 tanθ ≈ sinθ
由牛顿第二定律,得
故
解析
G
F
F合
类火车转弯
1.飞机转弯
O
mg
FN
f
汽车在水平地面上转弯是什么力提供向心力的呢
讨论
2.公路弯道
动力学方程
有的公路弯道处树立限速指示牌,为什么?设车轮与水平路面间动摩擦因数为μ,汽车速度不能超过多少?
当汽车转弯的半径一定时,
分析
Ff Ffm ,汽车将侧滑。
由此可见:当汽车转弯时,存在一个安全通过的最大速度,如果超过了这个速度,汽车将发生侧滑现象。
改进措施:
(1)增大转弯半径
(2)增加路面的粗糙程度
(3)最重要的一点:司机应该减速慢行!
(4)增加路面高度差——外高内低
思考:公路上的拱形桥是常见的,汽车过桥时,也可以看做圆周运动。
为什么凸形桥比凹形桥更普遍呢?
新课入
二、汽车过拱形桥
问题1:汽车过拱形桥时,在最高点时,车对凸桥的压力怎样?
mg
FN
,即处于失重。
F压 <mg
半径r
由牛顿第三定律得,汽车通过桥的最高点时对桥的压力:
汽车通过桥最高点时的向心力由什么力提供?
由 得,
重力和支持力的合力提供向心力
解析
讨论
⑴汽车处于超重还是失重状态?
当 FN = 0 时,汽车脱离桥面,做平抛运动,
汽车及其中的物体处于完全失重状态。
⑵汽车过拱形桥时,运动速度变大,车对凸桥的压力如何变化?
mg
FN
当 时,可过;
当 时,飞出。
v=
由 得,
结论:
⑶ FN=0 时,汽车的速度为多大?
称为安全行驶最大速度
v=
实例
问题2:汽车过凹形桥时,在最低点时,车对凹桥的压力又怎样?
FN
mg
汽车对桥的压力大于其所受重力,即处于超重。
F压 >mg
由牛顿第三定律得,汽车通过桥的最低点时对桥的压力:
汽车通过桥最低点时的向心力由什么力提供?
由 得,
汽车过凹形桥时需要有速度限制吗?
思考:
重力和支持力的合力提供向心力
解析
地球可以看作一个巨大的拱形桥,桥面的半径就是地球的半径 R(约为 6 400 km)。地面上有一辆汽车在行驶,所受重力 G = mg,地面对它的支持力是 FN 。
根据上面的分析,汽车速度越大,地面对它的支持力就越小。会不会出现这样的情况:速度大到一定程度时,地面对车的支持力是 0 ?这时驾驶员与座椅之间的压力是多少?驾驶员躯体各部分之间的压力是多少?他这时可能有什么感觉?
4
新课入
三、航天器中的失重现象
讨论
汽车车速为v,地球半径为R,
汽车对桥面的压力为0
代入g=9.8m/s2,R=6371km,得
v ≈ 7900m/s
当 时,
分析
R
在绕地球做匀速圆周运动的宇宙飞船中的宇航员,除了地球引力外,还可能受到飞船座舱对他的支持力 FN :
航天员处于完全失重状态。
由 得,
当 时,座舱对他的支持力 FN = 0。
R
实例:航天器中的失重现象
做圆周运动的物体,在提供的向心力突然消失,或者不足以提供圆周运动所需的向心力的情况下,就做逐渐远离圆心的运动。
新课入
四、离心运动
1.什么叫离心运动?
2.本质
做圆周运动的物体,由于本身惯性,总有沿着圆周切线飞出去的倾向。
F合=0 或 F供 < F需
是由指向圆心的合力来充当的,可以是重力、拉力、摩擦力等;
是由物体的运动速度来决定的,即:
F需 =
“供”“需”是否平衡决定物体是否做圆周运动
F供
F需
物体作离心运动的条件:
小结:
3.物体做离心运动的条件
当 F=mω2r 时,做匀速圆周运动;
当 F=0 时,沿切线方向飞出;
当 F<mω2r 时,逐渐远离圆心;
当 F>mω2r 时,逐渐靠近圆心。
分析:
F=0
F
F>mrω2
3.离心运动的应用和防止
洗衣机脱水时利用离心运动把附着在物体上的水分甩掉;纺织厂也用这样的方法使棉纱、毛线、纺织品干燥。
①洗衣机脱水
②棉花糖的制作
⑴离心运动的应用
③无缝钢管
在炼钢厂中,把熔化的钢水浇入圆柱形模子,模子沿圆柱的中心轴线高速旋转。
钢水由于离心运动趋于周壁,冷却后就形成无缝钢管。
高速旋转的飞轮、砂轮的限速
对于一些本身转动的物体也要预防离心现象例如:高速转动的砂轮、飞轮等,都不得超过允许的最大转速。
转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力,离心运动会使它们破裂,酿成事故。
高速转动的砂轮
⑵离心运动的防止
D
1.如图,某公路急转弯处是一圆弧,当汽车行驶的速率为vc时,汽车恰好没有向公路内外两侧滑动的趋势。则当汽车在该弯道处 ( )
A.车速低于vc时,车辆就向内侧滑动
B.车速高于vc时,车辆就向外侧滑动
C.路面结冰时,与未结冰时相比,vc的值变小
D.路面结冰时,与未结冰时相比,vc的值不变
课堂评价
2.如图所示,铁路在弯道处的内外轨道高低是不同的,已知内外轨组成的轨道平面与水平面的夹角为θ,弯道处的圆弧半径为R,若质量为m的火车以速度v通过某弯道时,内外轨道均不受侧压力作用,下面分析正确的是 ( )
A.
B.若火车速度大于v时,火车将受到外轨侧压力作用,其方向平行轨道平面向外
C.为解决火车高速转弯时外轨受损这一难题,可以适当增大弯道半径或适当增加内外轨的高度差
D.无论火车以何种速度行驶,对内侧轨道都有压力
C
3. 有一辆质量为 800kg 的小汽车驶上圆弧半径为 50 m 的拱桥。
⑴汽车到达桥顶时速度为5m/s,汽车对桥的压力是多大?
⑵汽车以多大速度经过桥顶时恰好腾空,对桥没有压力?
⑶汽车对地面的压力过小是不安全的。从这个角度讲,汽车过桥时的速度不能过大。对于同样的车速,拱桥圆弧的半径大些比较安全,还是小些比较安全?
⑷如果拱桥的半径增大到与地球半径R一样,汽车要在桥面上腾空,速度要多大?
1.火车转弯:v0= gR tanθ时,重力 G 和支持力 FN 的合力来提供火车转弯时所需的向心力。v>v0,外轨有挤压;v< v0,内轨有挤压。
2.拱桥: FN =mg-mv2/R
3.在所受合外力突然消失或不足以提供圆周运动所需向心力时F
离心运动的防止:汽车拐弯时限速。
新课入
课堂小结
