广东省深圳市高级中学2024-2025学年九年级上学期开学考数学试卷(无答案)
文档属性
| 名称 | 广东省深圳市高级中学2024-2025学年九年级上学期开学考数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 375.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-19 14:13:35 | ||
图片预览

文档简介
初三年级数学暑假作业反馈练习【2024-09-18】
班级:________________ 姓名:____________________
一、单选题(每题3分,共24分)
1.一元二次方程的解完全正确的是( )
A. B. C. D.
2.关于的一元二次方程有实数根,则的取值范围是( )
A. B. C., D.,
3.在一次兑换盲盒的游戏中,规定:在不透明的袋子中,放置3个黄球,2个红球,这些小球除颜色以外其他完全相同,搅匀后随机摸出两个球,若摸到的两个球颜色相同,便能得到一次兑换盲盒的机会,则参与者每次摸球得到兑换盲盒机会的概率是( )
A. B. C. D.
4.若关于的一元二次方程的一个根是,则代数式的值为( )
A. B.2018 C. D.2024
5.下列命题中正确的是( )
A.对角线互相垂直平分且相等的四边形是正方形 B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形 D.一组对边平行的四边形是平行四边形
6.如图,在矩形中,以点为圆心,的长为半径画弧,交于点E,再分别以点C,E为圆心,大于的长为半径画弧,两弧交于点,作射线交于点.若,,则的长为( )
A.5 B. C. D.
(6) (7)
7.某中学有一块长,宽的矩形空地.计划在这块空地上划出四分之一的区域种花.小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为,则可列方程为( )
A. B.
C. D.
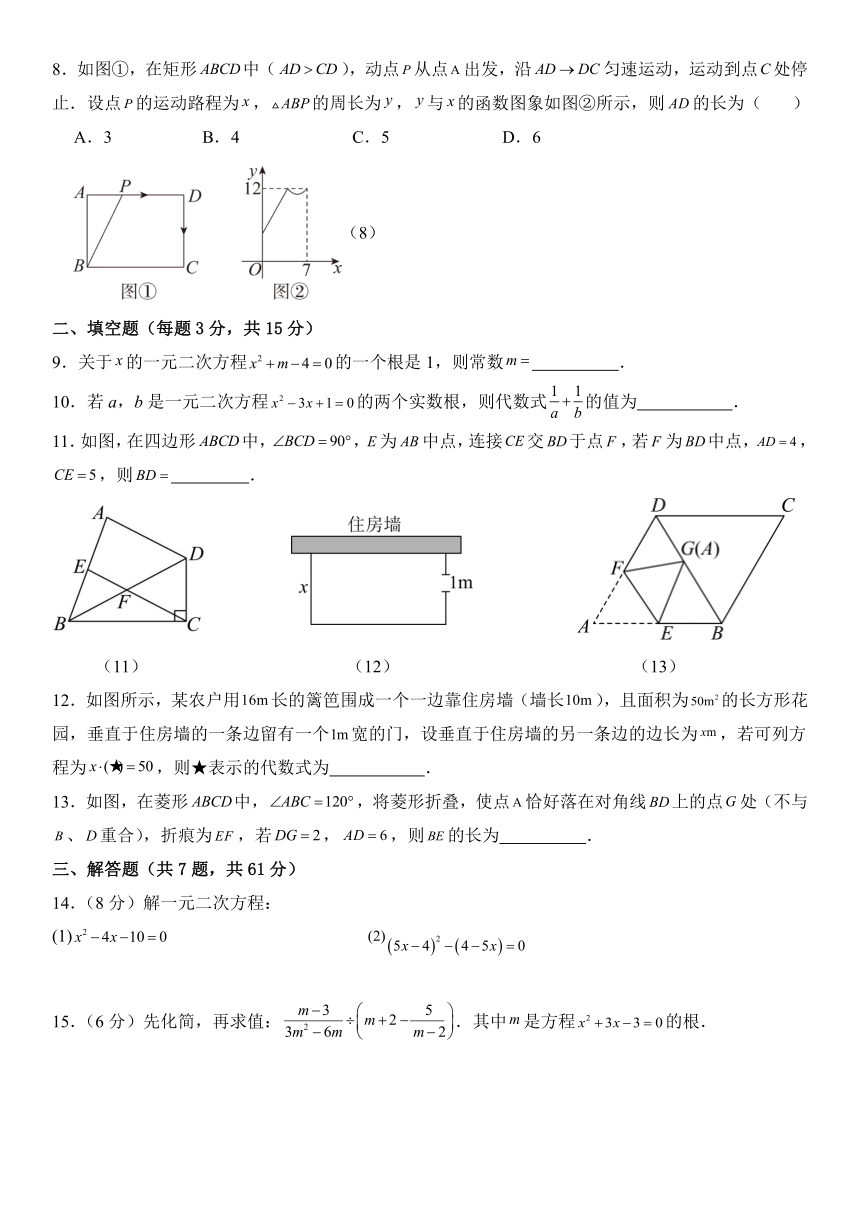
8.如图①,在矩形中(),动点从点出发,沿匀速运动,运动到点处停止.设点的运动路程为,的周长为,与的函数图象如图②所示,则的长为( )
A.3 B.4 C.5 D.6
(8)
二、填空题(每题3分,共15分)
9.关于的一元二次方程的一个根是1,则常数 .
10.若a,b是一元二次方程的两个实数根,则代数式的值为 .
11.如图,在四边形中,,为中点,连接交于点,若为中点,,,则 .
(11) (12) (13)
12.如图所示,某农户用长的篱笆围成一个一边靠住房墙(墙长),且面积为的长方形花园,垂直于住房墙的一条边留有一个宽的门,设垂直于住房墙的另一条边的边长为,若可列方程为,则★表示的代数式为 .
13.如图,在菱形中,,将菱形折叠,使点恰好落在对角线上的点处(不与、重合),折痕为,若,,则的长为 .
三、解答题(共7题,共61分)
14.(8分)解一元二次方程:
(1) (2)
15.(6分)先化简,再求值:.其中是方程的根.
16.(8分)2024年巴黎奥运会新增了四个项目:霹雳舞,滑板,冲浪,运动攀岩,依次记为A,B,C,D,滨河体育队的小明同学把这四个项目写在了背面完全相同的卡片上. 将这四张卡片背面朝上,洗匀放好.
(1)小明想从中随机抽取一张,去了解该项目在奥运会中的得分标准,恰好抽到是B(滑板)的概率是________.
(2)体育老师想从中选出来两个项目,让小明做成手抄报给大家普及一下,他先从中随机抽取一张不放回,再从中随机抽取一张,请用列表或画树状图的方法,求体育老师抽到的两张卡片恰好是B(滑板)和D(运动攀岩)的概率.
17.(8分)如图,在四边形中,,连接,,且经过的中点,点在上,且,连接,.
(1)求证:四边形是菱形(2)若,且,求菱形的面积.
18.(9分)栖霞某旅游景点的超市以每件元的价格购进某款果都吉祥物摆件,以每件元的价格出售.经统计,月份的销售量为件,月份的销售量为件.
(1)求该款吉祥物摆件月份到月份销售量的月平均增长率;
(2)从月份起,超市决定采用降价促销的方式回馈游客,经试验,发现该吉祥物摆件每降价元,月销售量就会增加件.当该吉祥物摆件售价为多少元时,月销售利润达元?
19.(10分)请认真阅读,并根据理解,完成相应任务:
阅读材料:
定义:若两个一元二次方程有且只有一个相同的实数根,我们就称这两个方程为“同伴方程”,例如:和有且只有一个相同的实数根,所以这两个方程为“同伴方程”.
任务一:
(1)根据所学定义,下列方程属于“同伴方程”的有______;(只填写序号即可)
① ;②;③.
任务二:
(2)关于的一元二次方程与为“同伴方程”,求的值;
任务三:
(3)若关于的一元二次方程()同时满足和,且与互为“同伴方程”,求的值.
20.(12分)我们定义:有一组邻边相等的四边形叫做“等邻边四边形”.
(1)如图1、点A,B,C在网格格点上,请你在网格图甲和乙中画出2个不同形状的等邻边四边形,要求顶点D在网格格点上;
(2)如图2,矩形中,,,点E在边上,连接,作于点F,若,找出图中的等邻边四边形,并说明理由;
(3)如图3,在中,,,,D是的中点,点M是边上一点(不与A,B重合),当四边形是等邻边四边形且为相等的邻边之一时,的长为 .
班级:________________ 姓名:____________________
一、单选题(每题3分,共24分)
1.一元二次方程的解完全正确的是( )
A. B. C. D.
2.关于的一元二次方程有实数根,则的取值范围是( )
A. B. C., D.,
3.在一次兑换盲盒的游戏中,规定:在不透明的袋子中,放置3个黄球,2个红球,这些小球除颜色以外其他完全相同,搅匀后随机摸出两个球,若摸到的两个球颜色相同,便能得到一次兑换盲盒的机会,则参与者每次摸球得到兑换盲盒机会的概率是( )
A. B. C. D.
4.若关于的一元二次方程的一个根是,则代数式的值为( )
A. B.2018 C. D.2024
5.下列命题中正确的是( )
A.对角线互相垂直平分且相等的四边形是正方形 B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形 D.一组对边平行的四边形是平行四边形
6.如图,在矩形中,以点为圆心,的长为半径画弧,交于点E,再分别以点C,E为圆心,大于的长为半径画弧,两弧交于点,作射线交于点.若,,则的长为( )
A.5 B. C. D.
(6) (7)
7.某中学有一块长,宽的矩形空地.计划在这块空地上划出四分之一的区域种花.小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为,则可列方程为( )
A. B.
C. D.
8.如图①,在矩形中(),动点从点出发,沿匀速运动,运动到点处停止.设点的运动路程为,的周长为,与的函数图象如图②所示,则的长为( )
A.3 B.4 C.5 D.6
(8)
二、填空题(每题3分,共15分)
9.关于的一元二次方程的一个根是1,则常数 .
10.若a,b是一元二次方程的两个实数根,则代数式的值为 .
11.如图,在四边形中,,为中点,连接交于点,若为中点,,,则 .
(11) (12) (13)
12.如图所示,某农户用长的篱笆围成一个一边靠住房墙(墙长),且面积为的长方形花园,垂直于住房墙的一条边留有一个宽的门,设垂直于住房墙的另一条边的边长为,若可列方程为,则★表示的代数式为 .
13.如图,在菱形中,,将菱形折叠,使点恰好落在对角线上的点处(不与、重合),折痕为,若,,则的长为 .
三、解答题(共7题,共61分)
14.(8分)解一元二次方程:
(1) (2)
15.(6分)先化简,再求值:.其中是方程的根.
16.(8分)2024年巴黎奥运会新增了四个项目:霹雳舞,滑板,冲浪,运动攀岩,依次记为A,B,C,D,滨河体育队的小明同学把这四个项目写在了背面完全相同的卡片上. 将这四张卡片背面朝上,洗匀放好.
(1)小明想从中随机抽取一张,去了解该项目在奥运会中的得分标准,恰好抽到是B(滑板)的概率是________.
(2)体育老师想从中选出来两个项目,让小明做成手抄报给大家普及一下,他先从中随机抽取一张不放回,再从中随机抽取一张,请用列表或画树状图的方法,求体育老师抽到的两张卡片恰好是B(滑板)和D(运动攀岩)的概率.
17.(8分)如图,在四边形中,,连接,,且经过的中点,点在上,且,连接,.
(1)求证:四边形是菱形(2)若,且,求菱形的面积.
18.(9分)栖霞某旅游景点的超市以每件元的价格购进某款果都吉祥物摆件,以每件元的价格出售.经统计,月份的销售量为件,月份的销售量为件.
(1)求该款吉祥物摆件月份到月份销售量的月平均增长率;
(2)从月份起,超市决定采用降价促销的方式回馈游客,经试验,发现该吉祥物摆件每降价元,月销售量就会增加件.当该吉祥物摆件售价为多少元时,月销售利润达元?
19.(10分)请认真阅读,并根据理解,完成相应任务:
阅读材料:
定义:若两个一元二次方程有且只有一个相同的实数根,我们就称这两个方程为“同伴方程”,例如:和有且只有一个相同的实数根,所以这两个方程为“同伴方程”.
任务一:
(1)根据所学定义,下列方程属于“同伴方程”的有______;(只填写序号即可)
① ;②;③.
任务二:
(2)关于的一元二次方程与为“同伴方程”,求的值;
任务三:
(3)若关于的一元二次方程()同时满足和,且与互为“同伴方程”,求的值.
20.(12分)我们定义:有一组邻边相等的四边形叫做“等邻边四边形”.
(1)如图1、点A,B,C在网格格点上,请你在网格图甲和乙中画出2个不同形状的等邻边四边形,要求顶点D在网格格点上;
(2)如图2,矩形中,,,点E在边上,连接,作于点F,若,找出图中的等邻边四边形,并说明理由;
(3)如图3,在中,,,,D是的中点,点M是边上一点(不与A,B重合),当四边形是等邻边四边形且为相等的邻边之一时,的长为 .
同课章节目录
