第11章 三角形 单元测试题(含答案)
文档属性
| 名称 | 第11章 三角形 单元测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 290.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十一章《三角形》单元检测题
一、选择题(每小题3分,共30分)
1、下列长度的3根小木棒不能搭成三角形的是( )
A.2cm,3cm,4cm B.1cm,2cm,3cm
C.3cm,4cm,5cm D.4cm,5cm,6cm
2、在△ABC中,∠A-∠C=∠B,那么△ABC是( )
A.等边三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
3.一个多边形的对角线共有27条,则这个多边形的边数是( )
A.8 B.9 C.10 D. 11
4.两根木棒分别为 和 ,要选择第三根,将它们钉成一个三角形,如果第三根木棒长为偶数,则方法有
A. 种 B. 种 C. 种 D. 种
5.如图所示,直线 ,,,则 的大小是
A. B. C. D.
6.如图,,,,则
A. B. C. D.
7.已知△ABC中,∠A=80°,∠B、∠C的平分线的夹角是( )
A.130° B.60° C.130°或50° D.60°或120°
8.如图,五角星的五个角之和,即:( )
A.180° B.90 C.270° D.240°
9.如图,在中,,,为中线.则与的周长之差为( )
A.1 B.2 C.3 D.4
10.如图,将一副三角尺按图中所示位置摆放,点在上,其中,,,,,则的度数是( )
A. B. C. D.
二、填空题(每题3分,共24分)
11.下列生产和生活实例:①用人字架来建筑房屋;②用窗钩来固定窗扇;③在栅栏门上斜钉着一根木条;④商店的推拉活动防盗门等.其中,用到三角形的稳定性的有 (填写序号).
12.正五边形的每一个内角的度数为 ;正五边形的每一个外角的度数为 .
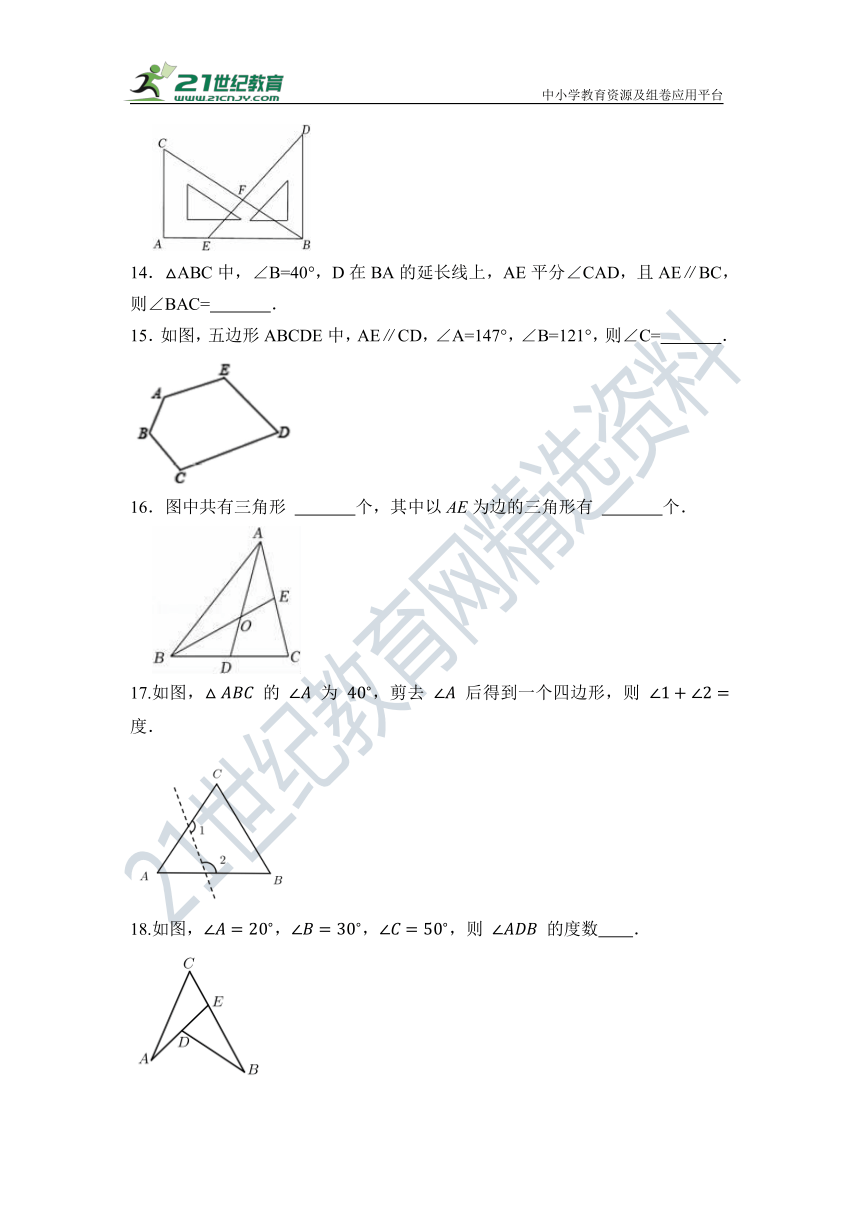
13.如图,一副三角尺按如图所示放置(∠C=60°,∠D=45°),则∠DFB= .
14.△ABC中,∠B=40°,D在BA的延长线上,AE平分∠CAD,且AE∥BC,则∠BAC= .
15.如图,五边形ABCDE中,AE∥CD,∠A=147°,∠B=121°,则∠C= .
16.图中共有三角形 个,其中以AE为边的三角形有 个.
17.如图, 的 为 ,剪去 后得到一个四边形,则 度.
18.如图,,,,则 的度数 .
三.解答题(共46分,19题6分,20 ---24题8分)
19、已知一个多边形每个内角都比它相邻外角大60°.
(1)求这个多边形的内角和;
(2)求这个多边形所有对角线的条数.
20、若一个多边形内角和与外角和的比为9∶2,求这个多边形的边数.
21.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=97°,求∠A和∠ACE的度数.
22.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;求证:CD⊥AB;
24.如图,在△ABC中,∠ABC=3∠C,AD平分∠BAC,BE⊥AD于E,若∠BAC=56°,求∠DBE的度数;
24.如图1,在三角形ABC中,∠ABC=90°,直线a与边AC、AB分别交于D、E两点,直线b与边BC、AC分别交于F、G两点,且a∥b.
(1)若∠AED=44°,求∠BFG的度数;
(2)如图2,P为边AB上一点,连结PF,若∠PFG+∠BFG=180°,请你探索∠PFG与∠AED的数量关系,并说明理由;
(3)如图3,若∠DEB=m,延长AB交直线b于点Q,在射线DC上有一动点P,连结PE、PQ,请直接写出∠PEQ、∠EPQ、PQF的数量关系(用含m的式子表示).
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B C B B C C B C
二、填空题
11.解:①用“人”字梁建筑屋顶,是利用三角形具有稳定性,符合题意;
②用窗钩来固定窗扇,是利用三角形具有稳定性,符合题意;
③在栅栏门上斜钉着一根木条,是利用三角形具有稳定性,符合题意;
④商店的推拉防盗铁门,是用四边形的不稳定性,不是用三角形具有稳定性,不符合题意;
综上所述:用到三角形稳定性的是①②③.
故答案为:①②③.
12.解:正五边形的内角是=108°,外角的度数是180°﹣108°=72°,
故答案为:108°,72°.
13.解:由题意得:∠BED=45°,∠ABC=30°,
∵∠DFB是△BEF的外角,
∴∠DFB=∠BED+∠ABC=75°.
故答案为:75°.
14.100°
15.92°
16.解:(1)①△BDO,△ABO,△AOE,共3个;
②△ABD,△ADC,2个;
③△ABE,△BCE,2个;
④△ABC,1个;
综上,图中共有共8个三角形;
(2)以AE为边的三角形有:△AOE,△ABE,2个;
故答案为:8;2.
17.
18.
三、解答题
19、 (1)720°
(2)9
20、11
21.解:∵∠ADB=∠DBC+∠ACB,
∴∠DBC=∠ADB-∠ACB=97°-60°=37°.
∵BD是∠ABC的平分线,
∴∠ABC=74°,
∴∠A=180°-∠ABC-∠ACB=46°.
∵CE是AB边上的高,
∴∠AEC=90°,
∴∠ACE=90°-∠A=44°.
22.
【分析】(1)利用三角形三边关系进而得出c的取值范围,进而得出答案;
(2)①根据偶数的定义,以及x的取值范围即可求解;
②利用等腰三角形的判定方法得出即可.
【解答】解:(1)因为a=4,b=6,
所以2<c<10.
故周长x的范围为12<x<20.
(2)①因为周长为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
【点评】此题主要考查了等腰三角形的判定和三角形三边关系,得出c的取值范围是解题关键.
23.解:∵∠BAC=56°,
∵AD平分∠BAC,
∴∠BAE=∠BAC=28°,
∴∠C+∠ABC=180°﹣56°=124°,
∵∠ABC=3∠C,
∴∠C=31°,
∴∠BAC=93°,
在Rt△ABE中,
∴∠ABE=62°,
∵∠DBE=∠ABC﹣∠ABE=93°﹣28°=65°.
24.解:延长AB交b于Q点,
∴∠AED=∠Q=44°,∠ABC=∠QBF=90°,
∴∠BFG=∠Q+∠QBF=44°+90°=134°.
(2)延长AB交b于Q点,
∵∠BFG+∠QFB=180°,
∴∠QFB=∠PFG,
在Rt△QFB中∠QFB+∠Q=90°,
∴∠PFG+∠Q=90°,
又∵∠AED=∠Q,
∴∠PFG+∠AED=90°,
(3)①当点P在DC的延长线上时,如图,
第十一章《三角形》单元检测题
一、选择题(每小题3分,共30分)
1、下列长度的3根小木棒不能搭成三角形的是( )
A.2cm,3cm,4cm B.1cm,2cm,3cm
C.3cm,4cm,5cm D.4cm,5cm,6cm
2、在△ABC中,∠A-∠C=∠B,那么△ABC是( )
A.等边三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
3.一个多边形的对角线共有27条,则这个多边形的边数是( )
A.8 B.9 C.10 D. 11
4.两根木棒分别为 和 ,要选择第三根,将它们钉成一个三角形,如果第三根木棒长为偶数,则方法有
A. 种 B. 种 C. 种 D. 种
5.如图所示,直线 ,,,则 的大小是
A. B. C. D.
6.如图,,,,则
A. B. C. D.
7.已知△ABC中,∠A=80°,∠B、∠C的平分线的夹角是( )
A.130° B.60° C.130°或50° D.60°或120°
8.如图,五角星的五个角之和,即:( )
A.180° B.90 C.270° D.240°
9.如图,在中,,,为中线.则与的周长之差为( )
A.1 B.2 C.3 D.4
10.如图,将一副三角尺按图中所示位置摆放,点在上,其中,,,,,则的度数是( )
A. B. C. D.
二、填空题(每题3分,共24分)
11.下列生产和生活实例:①用人字架来建筑房屋;②用窗钩来固定窗扇;③在栅栏门上斜钉着一根木条;④商店的推拉活动防盗门等.其中,用到三角形的稳定性的有 (填写序号).
12.正五边形的每一个内角的度数为 ;正五边形的每一个外角的度数为 .
13.如图,一副三角尺按如图所示放置(∠C=60°,∠D=45°),则∠DFB= .
14.△ABC中,∠B=40°,D在BA的延长线上,AE平分∠CAD,且AE∥BC,则∠BAC= .
15.如图,五边形ABCDE中,AE∥CD,∠A=147°,∠B=121°,则∠C= .
16.图中共有三角形 个,其中以AE为边的三角形有 个.
17.如图, 的 为 ,剪去 后得到一个四边形,则 度.
18.如图,,,,则 的度数 .
三.解答题(共46分,19题6分,20 ---24题8分)
19、已知一个多边形每个内角都比它相邻外角大60°.
(1)求这个多边形的内角和;
(2)求这个多边形所有对角线的条数.
20、若一个多边形内角和与外角和的比为9∶2,求这个多边形的边数.
21.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=97°,求∠A和∠ACE的度数.
22.如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;求证:CD⊥AB;
24.如图,在△ABC中,∠ABC=3∠C,AD平分∠BAC,BE⊥AD于E,若∠BAC=56°,求∠DBE的度数;
24.如图1,在三角形ABC中,∠ABC=90°,直线a与边AC、AB分别交于D、E两点,直线b与边BC、AC分别交于F、G两点,且a∥b.
(1)若∠AED=44°,求∠BFG的度数;
(2)如图2,P为边AB上一点,连结PF,若∠PFG+∠BFG=180°,请你探索∠PFG与∠AED的数量关系,并说明理由;
(3)如图3,若∠DEB=m,延长AB交直线b于点Q,在射线DC上有一动点P,连结PE、PQ,请直接写出∠PEQ、∠EPQ、PQF的数量关系(用含m的式子表示).
答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B C B B C C B C
二、填空题
11.解:①用“人”字梁建筑屋顶,是利用三角形具有稳定性,符合题意;
②用窗钩来固定窗扇,是利用三角形具有稳定性,符合题意;
③在栅栏门上斜钉着一根木条,是利用三角形具有稳定性,符合题意;
④商店的推拉防盗铁门,是用四边形的不稳定性,不是用三角形具有稳定性,不符合题意;
综上所述:用到三角形稳定性的是①②③.
故答案为:①②③.
12.解:正五边形的内角是=108°,外角的度数是180°﹣108°=72°,
故答案为:108°,72°.
13.解:由题意得:∠BED=45°,∠ABC=30°,
∵∠DFB是△BEF的外角,
∴∠DFB=∠BED+∠ABC=75°.
故答案为:75°.
14.100°
15.92°
16.解:(1)①△BDO,△ABO,△AOE,共3个;
②△ABD,△ADC,2个;
③△ABE,△BCE,2个;
④△ABC,1个;
综上,图中共有共8个三角形;
(2)以AE为边的三角形有:△AOE,△ABE,2个;
故答案为:8;2.
17.
18.
三、解答题
19、 (1)720°
(2)9
20、11
21.解:∵∠ADB=∠DBC+∠ACB,
∴∠DBC=∠ADB-∠ACB=97°-60°=37°.
∵BD是∠ABC的平分线,
∴∠ABC=74°,
∴∠A=180°-∠ABC-∠ACB=46°.
∵CE是AB边上的高,
∴∠AEC=90°,
∴∠ACE=90°-∠A=44°.
22.
【分析】(1)利用三角形三边关系进而得出c的取值范围,进而得出答案;
(2)①根据偶数的定义,以及x的取值范围即可求解;
②利用等腰三角形的判定方法得出即可.
【解答】解:(1)因为a=4,b=6,
所以2<c<10.
故周长x的范围为12<x<20.
(2)①因为周长为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
【点评】此题主要考查了等腰三角形的判定和三角形三边关系,得出c的取值范围是解题关键.
23.解:∵∠BAC=56°,
∵AD平分∠BAC,
∴∠BAE=∠BAC=28°,
∴∠C+∠ABC=180°﹣56°=124°,
∵∠ABC=3∠C,
∴∠C=31°,
∴∠BAC=93°,
在Rt△ABE中,
∴∠ABE=62°,
∵∠DBE=∠ABC﹣∠ABE=93°﹣28°=65°.
24.解:延长AB交b于Q点,
∴∠AED=∠Q=44°,∠ABC=∠QBF=90°,
∴∠BFG=∠Q+∠QBF=44°+90°=134°.
(2)延长AB交b于Q点,
∵∠BFG+∠QFB=180°,
∴∠QFB=∠PFG,
在Rt△QFB中∠QFB+∠Q=90°,
∴∠PFG+∠Q=90°,
又∵∠AED=∠Q,
∴∠PFG+∠AED=90°,
(3)①当点P在DC的延长线上时,如图,
