人教版(2019)必修第二册 6.4 生活中的圆周运动 课件(共37张PPT)
文档属性
| 名称 | 人教版(2019)必修第二册 6.4 生活中的圆周运动 课件(共37张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-20 14:05:54 | ||
图片预览








文档简介
(共37张PPT)
生活中的圆周运动
知识回顾
物体做圆周运动时,受力有何共同点
物体要受到指向圆心的向心力
向心力的特点
方向:总是指向圆心
大小:
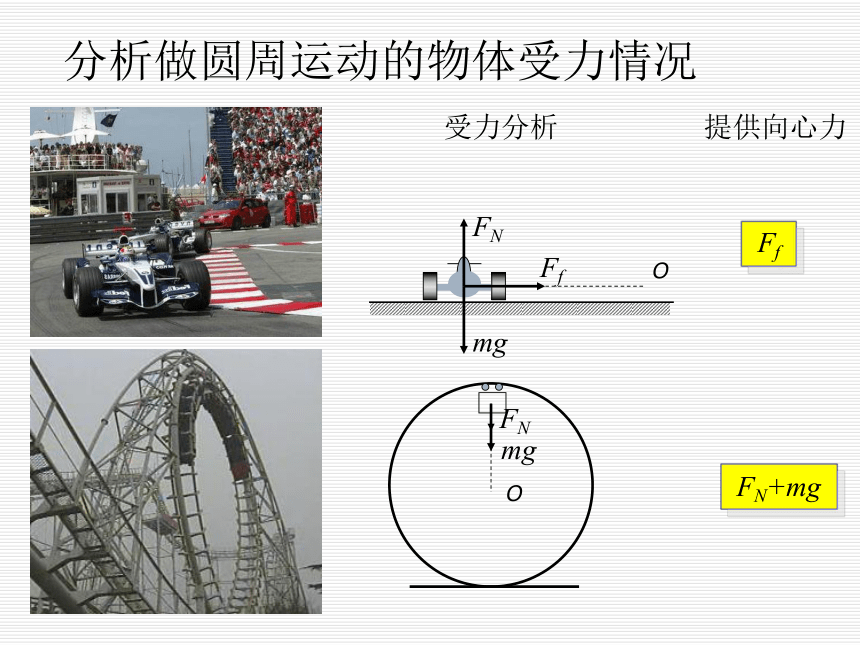
分析做圆周运动的物体受力情况
O
mg
FN
Ff
O
mg
FN
提供向心力
受力分析
Ff
FN+mg
F
“供需”平衡 物体做匀速圆周运动
提供物体做匀速圆周运动的力
物体做匀速圆周运动所需的力
向心力公式的理解
=
从“供” “需”两方面研究做圆周运动的物体
赛道的设计
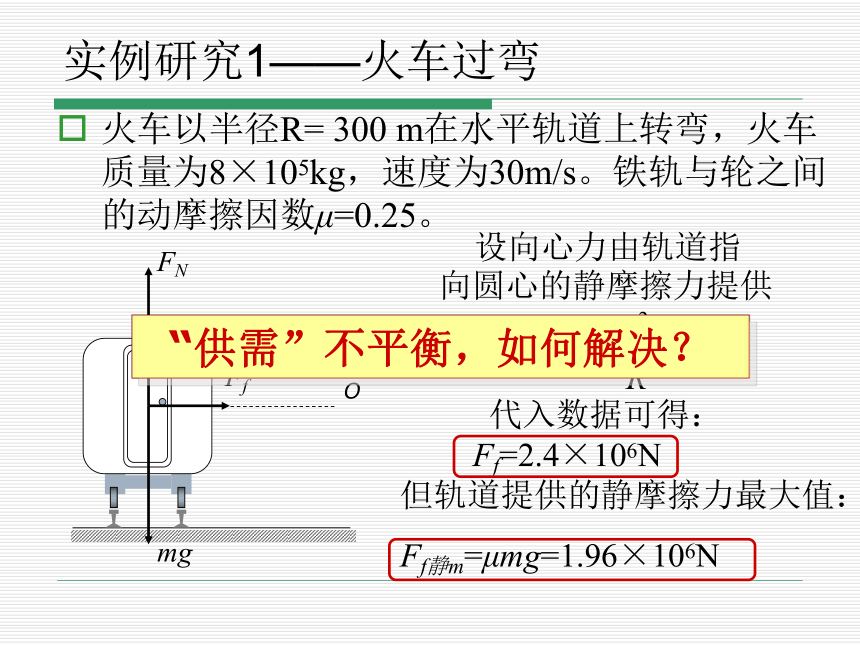
实例研究1——火车过弯
火车以半径R= 300 m在水平轨道上转弯,火车质量为8×105kg,速度为30m/s。铁轨与轮之间的动摩擦因数μ=0.25。
O
mg
FN
Ff
设向心力由轨道指向圆心的静摩擦力提供
代入数据可得: Ff=2.4×106N
但轨道提供的静摩擦力最大值:
Ff静m=μmg=1.96×106N
“供需”不平衡,如何解决?
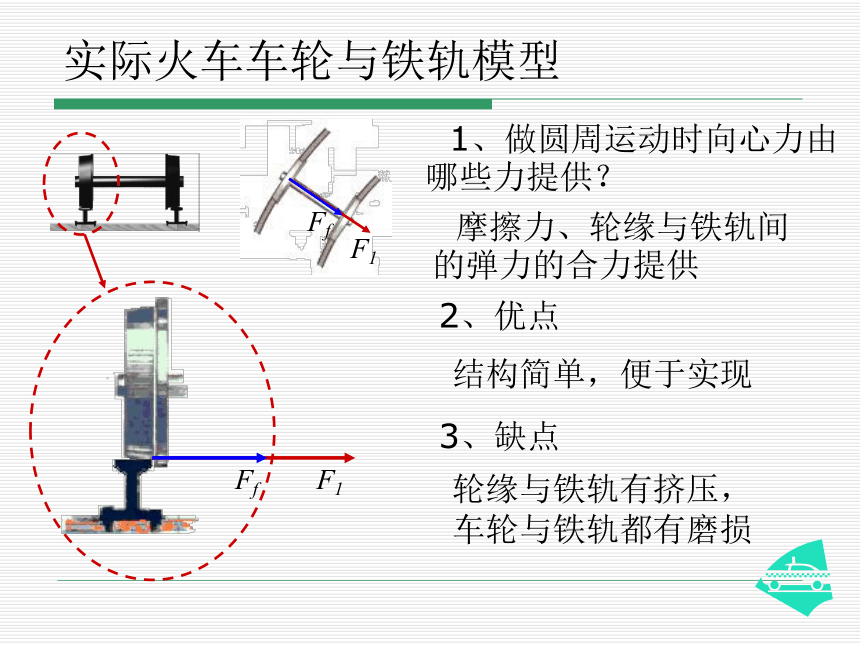
实际火车车轮与铁轨模型
2、优点
1、做圆周运动时向心力由哪些力提供?
摩擦力、轮缘与铁轨间的弹力的合力提供
F1
Ff
F1
Ff
3、缺点
结构简单,便于实现
轮缘与铁轨有挤压,车轮与铁轨都有磨损
垫高外轨
利用支持力的分力提供一部分向心力,达到“供需”平衡。
2、优点
1、做圆周运动时向心力由哪些力提供?
3、缺点
可以减少对摩擦力的需要
需要改造铁路,设计施工难度大
研究与讨论
1、请设计一个方案让火车沿轨道安全通过弯道?
实际火车与轨道设计中,
利用轮缘可增加小部分的向心力;
垫高外轨可增加较多的向心力。
2、最佳方案
火车以半径R= 900 m转弯,火车质量为8×105kg ,速度为30m/s,火车轨距l=1.4 m,要使火车通过弯道时仅受重力与轨道的支持力,轨道应该垫的高度h?
(θ较小时tanθ=sinθ)
FN
mg
F
θ
h
由力的关系得:
由向心力公式得:
由几何关系得:
解:
=0.14m
θ
例题3:如图所示,火车在转弯处需要的向心力很大,为此,在铺设轨道时让枕木与水平面成一夹角θ,如果火车以72km/h的速度通过此弯,转弯半径R=1km,求:θ应等于多少才能保证火车安全行驶?
研究与讨论
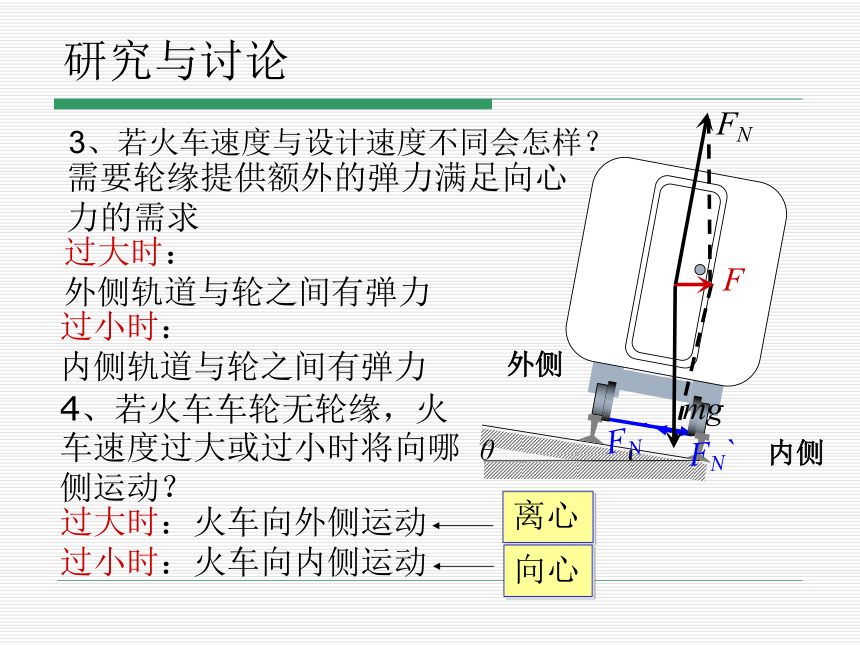
3、若火车速度与设计速度不同会怎样?
外侧
内侧
F
θ
过大时:
外侧轨道与轮之间有弹力
过小时:
内侧轨道与轮之间有弹力
需要轮缘提供额外的弹力满足向心力的需求
FN`
FN`
4、若火车车轮无轮缘,火车速度过大或过小时将向哪侧运动?
过大时:火车向外侧运动
过小时:火车向内侧运动
FN
mg
离心
向心
向心、圆周、离心运动
“供”“需”是否平衡决定物体做何种运动
供
提供物体做圆周运动的力
需
物体做匀速圆周运动所需的力
F=
匀速圆周运动
F<
离心运动
F>
向心运动
实例研究2——拱桥模型
1、汽车过拱桥是竖直面内圆周运动的典型代表
2、研究方法与水平面内圆周运动相同
实例2:汽车过拱桥的问题
mg
FN
当 时,
———说明什么问题?
汽车此时只受到重力作用同时具有水平速度
汽车做平抛运动
为了安全过桥汽车在桥顶的速度必须满足:
实例2:汽车过拱桥的问题
mg
FN
实例2:汽车过拱桥的问题
mg
FN
mg
FN
比较在两种不同桥面,桥面受力的情况,设车质量为m,桥面半径为R,此时速度为v。
G
FN
G
FN’
失重
超重
a
a
最高点
最低点
说明: 上述过程中汽车做的不是匀速圆周运动,我们仍使用了匀速圆周运动的公式,原因是向心力和向心加速度的公式对于变速圆周运动同样适用。
在变速圆周运动中,利用上面的公式求质点在圆周上某一点的向心力和向心加速度的大小,必须利用该点的瞬时速度值。
研究与讨论
1、若速度过快,汽车做何种运动?
提供的向心力不足,做离心运动,离开桥面做平抛运动
2、有无可能做这样的运动?若可能应满足怎样的条件?
G
FN
过山车
水流星
mg
FN
mg
FN
最高点:
又因为
即
在细线拉力的作用下,在竖直平面内完成圆
周运动则在最高点须满足
最低点:
实例研究3——绳拉小球模型
实例研究4——杆拉小球模型
mg
FN
mg
FN
最高点:
杆对球无作用力
杆对球有拉力作用
杆对球有支持力作用
最低点:
研究圆周运动的要点
从“供”“需”两方面来进行研究
“供”——分析物体受力,求沿半径方向的合外力
“需”——确定物体轨道,定圆心、找半径、用公式,求出所需向心力
“供”“需”平衡做圆周运动
练习2 飞车走壁
摩托车飞车走壁,请分析受力情况,解释现象
1.在水平面上转弯的汽车,向心力是( )
A.重力和支持力的合力
B.静摩擦力
C.滑动摩擦力
D.重力、支持力和牵引的的合力
B
四.巩固练习
2.用长为L的细绳,拴着质量为m的小球,在竖
直平面内做圆周运动,则下列说法中正确的是
( )
A.小球在最高点所受的向心力一定是重力
B.小球在最高点时绳子的拉力可能为零
C.小球刚好在竖直平面内做圆周运动,则经过最
高点的速率是
BC
3.一汽车通过拱形桥顶点时的速度为10m/s,车对
桥顶的压力为车重的3/4,如果要使汽车在桥顶对
桥面没有压力,车速至少为( )
A.15m/s B.20m/s
C.25m/s D.30m/s
B
4质量为m的小球,用一条绳子系着在竖直平面内
做圆周运动,小球到最高点时的速度为v,到达最
低点时的速度为 ,则小球通过上述两
位置处时绳子所受的张力之差是( )
A.6mg B.5mg
C.4mg D.2mg
A
5.如图,圆锥摆摆长为L,摆角为α,质且为m的
摆球在水平面内作匀速圆周运动,则( )
A.摆线的拉力为mg/cosα
B.摆球的向心加速度为gcosα
C.其周期为2π
D.其周期为2π
AD
自行车转弯时,稍一倾斜就过去了,摩托车转弯倾斜度要大一些。摩托赛车时转弯,倾斜度更大,几乎倒在地上。
问:什么力提供向心力?向心力与倾斜度有关吗?有何关系?
解答:
由地面对车的静摩擦力提供
有关系,倾斜度越大,向心力越大
例 m=5000kg 的汽车,通过半径R=50m的拱型桥顶时速度为5m/s.则汽车对桥顶的压力是多少
汽车在倾斜的弯道上拐弯,弯道的倾角为θ,半径为r,则汽车完全不靠摩擦力转弯的速率是多大
汽车在半径为r的水平弯道上转弯,如果汽车与地面的动摩擦因数为μ,那么汽车不发生侧滑的最大速率是多大
长0.8m的细绳悬挂一盛水的小桶,小桶的质量是1kg,桶中盛有水2kg,手拿另一端使小桶在竖直片面内做圆周运动,小桶在最高点的线速度最小是多少
练习3
如图为过山车轨道的一部分,若要使车厢能安全通过圆形轨道,车厢应从多高处释放?不计一切摩擦与阻力。
R
h?
讨论
3、若汽车沿圆弧桥面从顶端下滑,分析汽车的运动情况。
θ
R
分析:由物体重力及支持力沿半径方向的合外力提供向心力,若车速度过快,车会离开桥面做斜下抛运动
即将离开时FN=0
生活中的圆周运动
知识回顾
物体做圆周运动时,受力有何共同点
物体要受到指向圆心的向心力
向心力的特点
方向:总是指向圆心
大小:
分析做圆周运动的物体受力情况
O
mg
FN
Ff
O
mg
FN
提供向心力
受力分析
Ff
FN+mg
F
“供需”平衡 物体做匀速圆周运动
提供物体做匀速圆周运动的力
物体做匀速圆周运动所需的力
向心力公式的理解
=
从“供” “需”两方面研究做圆周运动的物体
赛道的设计
实例研究1——火车过弯
火车以半径R= 300 m在水平轨道上转弯,火车质量为8×105kg,速度为30m/s。铁轨与轮之间的动摩擦因数μ=0.25。
O
mg
FN
Ff
设向心力由轨道指向圆心的静摩擦力提供
代入数据可得: Ff=2.4×106N
但轨道提供的静摩擦力最大值:
Ff静m=μmg=1.96×106N
“供需”不平衡,如何解决?
实际火车车轮与铁轨模型
2、优点
1、做圆周运动时向心力由哪些力提供?
摩擦力、轮缘与铁轨间的弹力的合力提供
F1
Ff
F1
Ff
3、缺点
结构简单,便于实现
轮缘与铁轨有挤压,车轮与铁轨都有磨损
垫高外轨
利用支持力的分力提供一部分向心力,达到“供需”平衡。
2、优点
1、做圆周运动时向心力由哪些力提供?
3、缺点
可以减少对摩擦力的需要
需要改造铁路,设计施工难度大
研究与讨论
1、请设计一个方案让火车沿轨道安全通过弯道?
实际火车与轨道设计中,
利用轮缘可增加小部分的向心力;
垫高外轨可增加较多的向心力。
2、最佳方案
火车以半径R= 900 m转弯,火车质量为8×105kg ,速度为30m/s,火车轨距l=1.4 m,要使火车通过弯道时仅受重力与轨道的支持力,轨道应该垫的高度h?
(θ较小时tanθ=sinθ)
FN
mg
F
θ
h
由力的关系得:
由向心力公式得:
由几何关系得:
解:
=0.14m
θ
例题3:如图所示,火车在转弯处需要的向心力很大,为此,在铺设轨道时让枕木与水平面成一夹角θ,如果火车以72km/h的速度通过此弯,转弯半径R=1km,求:θ应等于多少才能保证火车安全行驶?
研究与讨论
3、若火车速度与设计速度不同会怎样?
外侧
内侧
F
θ
过大时:
外侧轨道与轮之间有弹力
过小时:
内侧轨道与轮之间有弹力
需要轮缘提供额外的弹力满足向心力的需求
FN`
FN`
4、若火车车轮无轮缘,火车速度过大或过小时将向哪侧运动?
过大时:火车向外侧运动
过小时:火车向内侧运动
FN
mg
离心
向心
向心、圆周、离心运动
“供”“需”是否平衡决定物体做何种运动
供
提供物体做圆周运动的力
需
物体做匀速圆周运动所需的力
F=
匀速圆周运动
F<
离心运动
F>
向心运动
实例研究2——拱桥模型
1、汽车过拱桥是竖直面内圆周运动的典型代表
2、研究方法与水平面内圆周运动相同
实例2:汽车过拱桥的问题
mg
FN
当 时,
———说明什么问题?
汽车此时只受到重力作用同时具有水平速度
汽车做平抛运动
为了安全过桥汽车在桥顶的速度必须满足:
实例2:汽车过拱桥的问题
mg
FN
实例2:汽车过拱桥的问题
mg
FN
mg
FN
比较在两种不同桥面,桥面受力的情况,设车质量为m,桥面半径为R,此时速度为v。
G
FN
G
FN’
失重
超重
a
a
最高点
最低点
说明: 上述过程中汽车做的不是匀速圆周运动,我们仍使用了匀速圆周运动的公式,原因是向心力和向心加速度的公式对于变速圆周运动同样适用。
在变速圆周运动中,利用上面的公式求质点在圆周上某一点的向心力和向心加速度的大小,必须利用该点的瞬时速度值。
研究与讨论
1、若速度过快,汽车做何种运动?
提供的向心力不足,做离心运动,离开桥面做平抛运动
2、有无可能做这样的运动?若可能应满足怎样的条件?
G
FN
过山车
水流星
mg
FN
mg
FN
最高点:
又因为
即
在细线拉力的作用下,在竖直平面内完成圆
周运动则在最高点须满足
最低点:
实例研究3——绳拉小球模型
实例研究4——杆拉小球模型
mg
FN
mg
FN
最高点:
杆对球无作用力
杆对球有拉力作用
杆对球有支持力作用
最低点:
研究圆周运动的要点
从“供”“需”两方面来进行研究
“供”——分析物体受力,求沿半径方向的合外力
“需”——确定物体轨道,定圆心、找半径、用公式,求出所需向心力
“供”“需”平衡做圆周运动
练习2 飞车走壁
摩托车飞车走壁,请分析受力情况,解释现象
1.在水平面上转弯的汽车,向心力是( )
A.重力和支持力的合力
B.静摩擦力
C.滑动摩擦力
D.重力、支持力和牵引的的合力
B
四.巩固练习
2.用长为L的细绳,拴着质量为m的小球,在竖
直平面内做圆周运动,则下列说法中正确的是
( )
A.小球在最高点所受的向心力一定是重力
B.小球在最高点时绳子的拉力可能为零
C.小球刚好在竖直平面内做圆周运动,则经过最
高点的速率是
BC
3.一汽车通过拱形桥顶点时的速度为10m/s,车对
桥顶的压力为车重的3/4,如果要使汽车在桥顶对
桥面没有压力,车速至少为( )
A.15m/s B.20m/s
C.25m/s D.30m/s
B
4质量为m的小球,用一条绳子系着在竖直平面内
做圆周运动,小球到最高点时的速度为v,到达最
低点时的速度为 ,则小球通过上述两
位置处时绳子所受的张力之差是( )
A.6mg B.5mg
C.4mg D.2mg
A
5.如图,圆锥摆摆长为L,摆角为α,质且为m的
摆球在水平面内作匀速圆周运动,则( )
A.摆线的拉力为mg/cosα
B.摆球的向心加速度为gcosα
C.其周期为2π
D.其周期为2π
AD
自行车转弯时,稍一倾斜就过去了,摩托车转弯倾斜度要大一些。摩托赛车时转弯,倾斜度更大,几乎倒在地上。
问:什么力提供向心力?向心力与倾斜度有关吗?有何关系?
解答:
由地面对车的静摩擦力提供
有关系,倾斜度越大,向心力越大
例 m=5000kg 的汽车,通过半径R=50m的拱型桥顶时速度为5m/s.则汽车对桥顶的压力是多少
汽车在倾斜的弯道上拐弯,弯道的倾角为θ,半径为r,则汽车完全不靠摩擦力转弯的速率是多大
汽车在半径为r的水平弯道上转弯,如果汽车与地面的动摩擦因数为μ,那么汽车不发生侧滑的最大速率是多大
长0.8m的细绳悬挂一盛水的小桶,小桶的质量是1kg,桶中盛有水2kg,手拿另一端使小桶在竖直片面内做圆周运动,小桶在最高点的线速度最小是多少
练习3
如图为过山车轨道的一部分,若要使车厢能安全通过圆形轨道,车厢应从多高处释放?不计一切摩擦与阻力。
R
h?
讨论
3、若汽车沿圆弧桥面从顶端下滑,分析汽车的运动情况。
θ
R
分析:由物体重力及支持力沿半径方向的合外力提供向心力,若车速度过快,车会离开桥面做斜下抛运动
即将离开时FN=0
