人教版(2019)必修第二册 6.2 向心力 课件(共22张PPT)
文档属性
| 名称 | 人教版(2019)必修第二册 6.2 向心力 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-20 14:11:37 | ||
图片预览




文档简介
(共22张PPT)
曲线运动
向心力
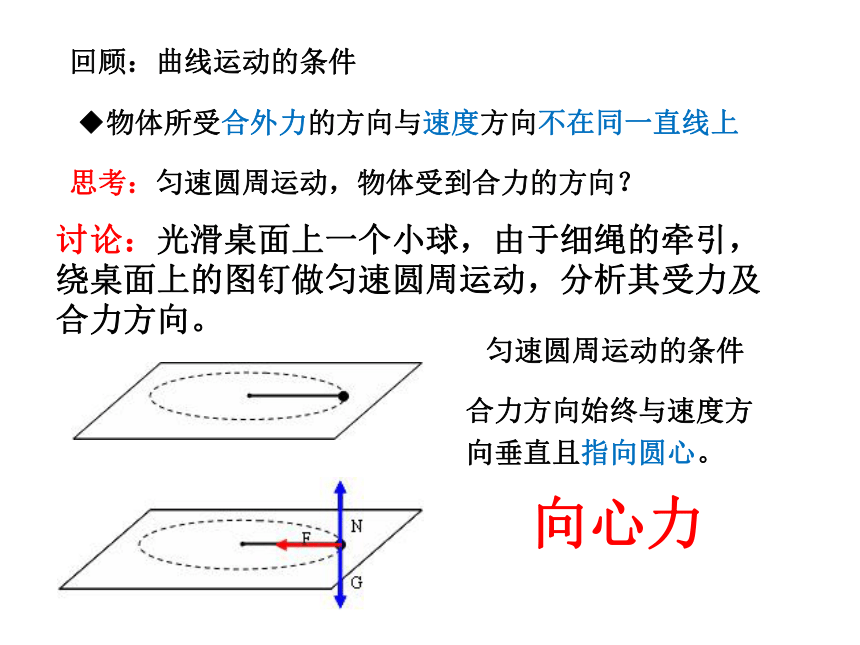
讨论:光滑桌面上一个小球,由于细绳的牵引,绕桌面上的图钉做匀速圆周运动,分析其受力及合力方向。
思考:匀速圆周运动,物体受到合力的方向?
回顾:曲线运动的条件
◆物体所受合外力的方向与速度方向不在同一直线上
合力方向始终与速度方向垂直且指向圆心。
向心力
匀速圆周运动的条件
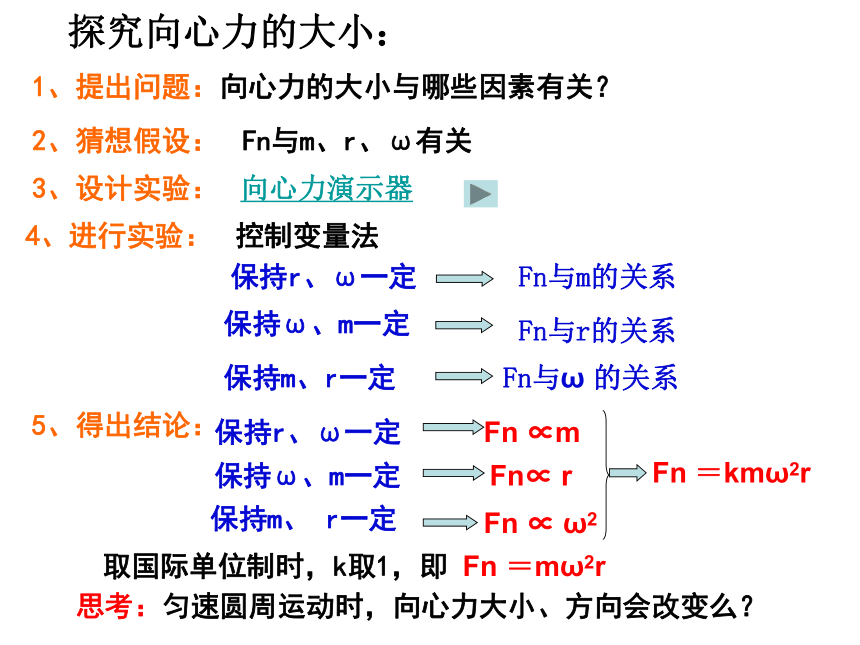
探究向心力的大小:
1、提出问题:向心力的大小与哪些因素有关?
2、猜想假设:
Fn与m、r、ω有关
3、设计实验:
4、进行实验:
控制变量法
保持ω、m一定
Fn与r的关系
保持m、r一定
Fn与ω 的关系
保持r、ω一定
Fn与m的关系
5、得出结论:
保持ω、m一定
Fn ∝ ω2
保持m、 r一定
Fn∝ r
保持r、ω一定
Fn ∝m
Fn =kmω2r
向心力演示器
取国际单位制时,k取1,即 Fn =mω2r
思考:匀速圆周运动时,向心力大小、方向会改变么?
1、匀速圆周运动条件:合外力大小不变,方向始终与
速度方向垂直且指向圆心。
2、向心力来源:向心力可以是重力、弹力、摩擦力、
等各种力,也可以是各力的合力或某力的分力,总之,
只要达到维持物体作圆周运动效果的力,就是向心力。
向心力是按力的作用效果来命名的。
3、向心力作用效果:产生向心加速度,只改变速度
方向,不改变速率。
几个有用的结论
4、向心力公式:
Fn =mω2r
(2)由F合=ma,a向心加速度,F合为向心力,即得:
(1)实验探究得:
做匀速圆周运动时,物体所受的合力总是指向圆心,这时合力就等于向心力。
2.一般的曲线运动
(1)一般的曲线运动:轨迹既不是直线也不是圆周的曲线运动。
(2)一般曲线运动的处理方法:
①把曲线分割成许多小段
②质点在每一小段的运动都可以看作圆周运动的一部分
③分析质点经过某位置的运动时,可用圆周运动的分析方法来处理。
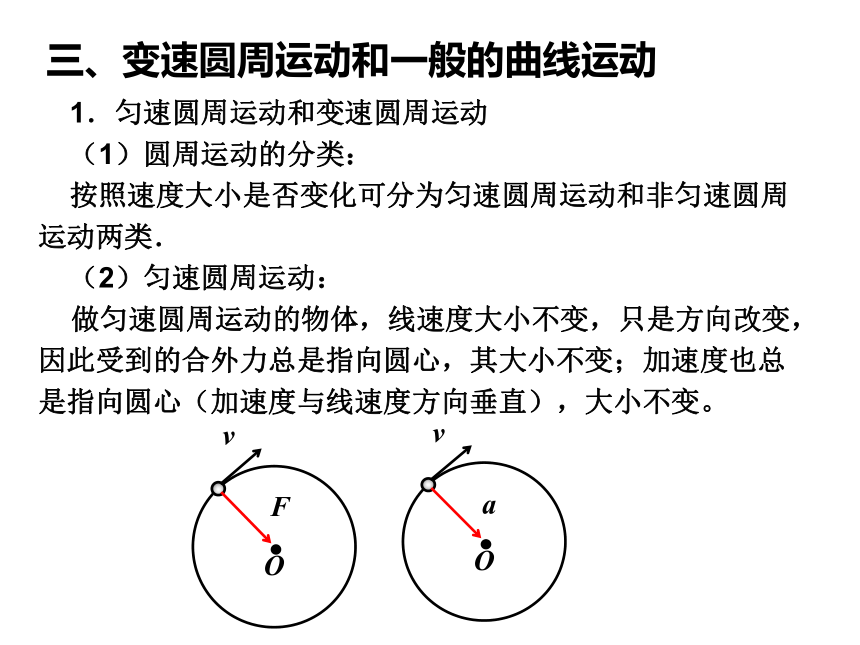
三、变速圆周运动和一般的曲线运动
1.匀速圆周运动和变速圆周运动
(1)圆周运动的分类:
按照速度大小是否变化可分为匀速圆周运动和非匀速圆周运动两类.
(2)匀速圆周运动:
做匀速圆周运动的物体,线速度大小不变,只是方向改变,因此受到的合外力总是指向圆心,其大小不变;加速度也总是指向圆心(加速度与线速度方向垂直),大小不变。
O
F
v
O
a
v
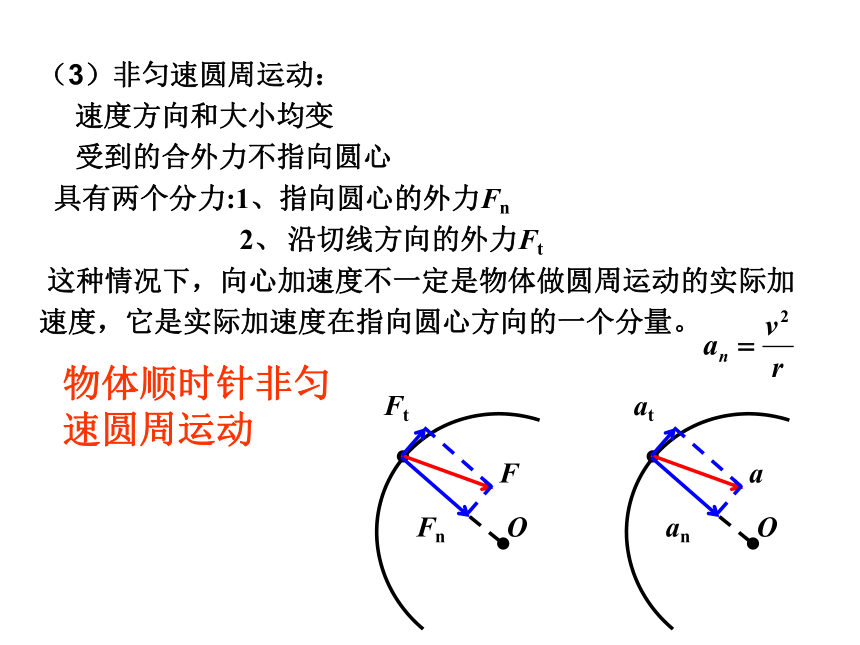
(3)非匀速圆周运动:
速度方向和大小均变
受到的合外力不指向圆心
具有两个分力:1、指向圆心的外力Fn
2、 沿切线方向的外力Ft
这种情况下,向心加速度不一定是物体做圆周运动的实际加速度,它是实际加速度在指向圆心方向的一个分量。
O
F
Fn
Ft
O
a
an
at
物体顺时针非匀速圆周运动
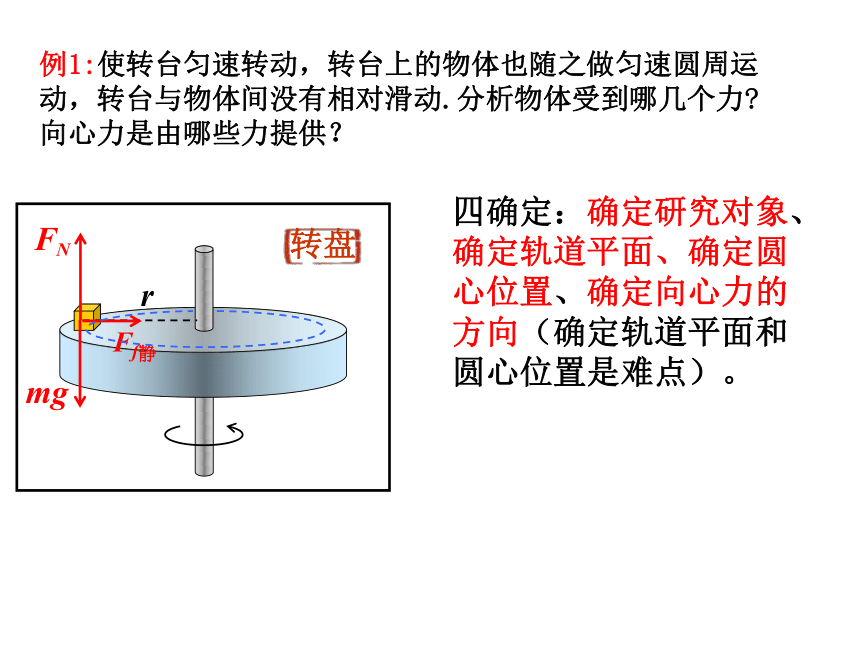
mg
FN
r
Ff静
转盘
例1:使转台匀速转动,转台上的物体也随之做匀速圆周运动,转台与物体间没有相对滑动.分析物体受到哪几个力 向心力是由哪些力提供?
四确定:确定研究对象、确定轨道平面、确定圆心位置、确定向心力的方向(确定轨道平面和圆心位置是难点)。
O
θ
O'
FT
mg
F合
圆锥摆
例2:圆锥摆运动:细线下面悬挂一钢球,细线上端固定,设法使小球在水平面面上做匀速圆周运动.分析物体受到哪几个力 向心力是由哪些力提供?
r
mg
Ff静
O
FN
滚筒
例4:如图所示,半径为r的圆筒绕轴以角速度ω匀速转动,物体m与圆筒壁之间有摩擦.分析物体受到哪几个力 向心力是由哪些力提供?
做匀速圆周运动时,物体所受的合力总是指向圆心,这时合力就等于向心力。
θ
O
r
mg
FN
F合
圆台筒
例3:玻璃球沿碗(透明)的内壁在水平面内匀速圆周运动;或者漏斗里的匀速圆周运动,如图。(不计摩擦)分析物体受到哪几个力 向心力是由哪些力提供?
N
mg
F
mg
N
θ
第一步:1、研究对象为A、B。2、两球轨道平面是水平的;3、它们的圆心均在转轴上;4、它们的向心力均在各自的水平轨道平面内指向各自圆心。
第二步:小球A和B的受力分析如图。
第三步:列方程。
(两球向心力相等)
一、匀速圆周运动的实例分析
AB
应用步骤:
(1)四确定:确定研究对象、确定轨道平面、确定
圆心位置、确定向心力的方向(确定轨道平面和圆
心位置是难点)。
(2)受力分析(不要把向心力作为某一性质的力进
行分析)写出合外力表达式。
(3)选定向心力方向列方程。
OVER
如图示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则:( )
N
mg
F
mg
N
θ
A、球A的线速度必定大于球B 的线速度。
B、球A的角速度必定小于球B的角速度。
C、球A的运动周期必定小于球B的运动周期。
D、球A对筒的压力必定大于球B对筒的压力。
E、球A的运动频率大于球B的运动频率。
第一步:1、研究对象为A、B。2、两球轨道平面是水平的;3、它们的圆心均在转轴上;4、它们的向心力均在各自的水平轨道平面内指向各自圆心。
第二步:小球A和B的受力分析如图。
θ
第三步:列方程。
(两球向心力相等)
AB
对下列作圆周运动的物体受力分析,并指出什么力(或什么
力在什么方向上的分力)提供向心力。
1、物体在水平方向的圆周运动。
mg
T
mg
T
mg
f
N
2、涉及摩擦力的圆周运动
f
o
T
f
r
o
设物体M和水平面保持相对静止。当ω具有最小值时, M有向圆心运动的趋势故水平面对M的摩擦力方向和指向圆心方向相反,且等于最大静摩擦力2 N。
当ω有最大值时, M有离开圆心的趋势,水平面对M的摩擦力的
方向指向圆心反向,大小也为2 N。
如图示,细绳一端系着质量为M=0.6kg的物体,静止
在水平面,另一端通过光滑小孔掉着质量为m=0.3kg
的物体,M的中点与圆孔距离为0.2m,并知M和水平
面的最大静摩擦力为2N,现使此平面绕中心轴线转动
问角速度在什么范围m会处于静止状态?g=10m/S2
弹簧测力套筒
转动手柄
长
槽
短
槽
小球
三层变速塔轮
标尺
挡板
弹簧测力套筒
(2)有一种叫“飞椅”的游乐项目,示意图如图14所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ,不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.
2008年广东物理卷
二、运动模型的建立
曲线运动
向心力
讨论:光滑桌面上一个小球,由于细绳的牵引,绕桌面上的图钉做匀速圆周运动,分析其受力及合力方向。
思考:匀速圆周运动,物体受到合力的方向?
回顾:曲线运动的条件
◆物体所受合外力的方向与速度方向不在同一直线上
合力方向始终与速度方向垂直且指向圆心。
向心力
匀速圆周运动的条件
探究向心力的大小:
1、提出问题:向心力的大小与哪些因素有关?
2、猜想假设:
Fn与m、r、ω有关
3、设计实验:
4、进行实验:
控制变量法
保持ω、m一定
Fn与r的关系
保持m、r一定
Fn与ω 的关系
保持r、ω一定
Fn与m的关系
5、得出结论:
保持ω、m一定
Fn ∝ ω2
保持m、 r一定
Fn∝ r
保持r、ω一定
Fn ∝m
Fn =kmω2r
向心力演示器
取国际单位制时,k取1,即 Fn =mω2r
思考:匀速圆周运动时,向心力大小、方向会改变么?
1、匀速圆周运动条件:合外力大小不变,方向始终与
速度方向垂直且指向圆心。
2、向心力来源:向心力可以是重力、弹力、摩擦力、
等各种力,也可以是各力的合力或某力的分力,总之,
只要达到维持物体作圆周运动效果的力,就是向心力。
向心力是按力的作用效果来命名的。
3、向心力作用效果:产生向心加速度,只改变速度
方向,不改变速率。
几个有用的结论
4、向心力公式:
Fn =mω2r
(2)由F合=ma,a向心加速度,F合为向心力,即得:
(1)实验探究得:
做匀速圆周运动时,物体所受的合力总是指向圆心,这时合力就等于向心力。
2.一般的曲线运动
(1)一般的曲线运动:轨迹既不是直线也不是圆周的曲线运动。
(2)一般曲线运动的处理方法:
①把曲线分割成许多小段
②质点在每一小段的运动都可以看作圆周运动的一部分
③分析质点经过某位置的运动时,可用圆周运动的分析方法来处理。
三、变速圆周运动和一般的曲线运动
1.匀速圆周运动和变速圆周运动
(1)圆周运动的分类:
按照速度大小是否变化可分为匀速圆周运动和非匀速圆周运动两类.
(2)匀速圆周运动:
做匀速圆周运动的物体,线速度大小不变,只是方向改变,因此受到的合外力总是指向圆心,其大小不变;加速度也总是指向圆心(加速度与线速度方向垂直),大小不变。
O
F
v
O
a
v
(3)非匀速圆周运动:
速度方向和大小均变
受到的合外力不指向圆心
具有两个分力:1、指向圆心的外力Fn
2、 沿切线方向的外力Ft
这种情况下,向心加速度不一定是物体做圆周运动的实际加速度,它是实际加速度在指向圆心方向的一个分量。
O
F
Fn
Ft
O
a
an
at
物体顺时针非匀速圆周运动
mg
FN
r
Ff静
转盘
例1:使转台匀速转动,转台上的物体也随之做匀速圆周运动,转台与物体间没有相对滑动.分析物体受到哪几个力 向心力是由哪些力提供?
四确定:确定研究对象、确定轨道平面、确定圆心位置、确定向心力的方向(确定轨道平面和圆心位置是难点)。
O
θ
O'
FT
mg
F合
圆锥摆
例2:圆锥摆运动:细线下面悬挂一钢球,细线上端固定,设法使小球在水平面面上做匀速圆周运动.分析物体受到哪几个力 向心力是由哪些力提供?
r
mg
Ff静
O
FN
滚筒
例4:如图所示,半径为r的圆筒绕轴以角速度ω匀速转动,物体m与圆筒壁之间有摩擦.分析物体受到哪几个力 向心力是由哪些力提供?
做匀速圆周运动时,物体所受的合力总是指向圆心,这时合力就等于向心力。
θ
O
r
mg
FN
F合
圆台筒
例3:玻璃球沿碗(透明)的内壁在水平面内匀速圆周运动;或者漏斗里的匀速圆周运动,如图。(不计摩擦)分析物体受到哪几个力 向心力是由哪些力提供?
N
mg
F
mg
N
θ
第一步:1、研究对象为A、B。2、两球轨道平面是水平的;3、它们的圆心均在转轴上;4、它们的向心力均在各自的水平轨道平面内指向各自圆心。
第二步:小球A和B的受力分析如图。
第三步:列方程。
(两球向心力相等)
一、匀速圆周运动的实例分析
AB
应用步骤:
(1)四确定:确定研究对象、确定轨道平面、确定
圆心位置、确定向心力的方向(确定轨道平面和圆
心位置是难点)。
(2)受力分析(不要把向心力作为某一性质的力进
行分析)写出合外力表达式。
(3)选定向心力方向列方程。
OVER
如图示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,有两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则:( )
N
mg
F
mg
N
θ
A、球A的线速度必定大于球B 的线速度。
B、球A的角速度必定小于球B的角速度。
C、球A的运动周期必定小于球B的运动周期。
D、球A对筒的压力必定大于球B对筒的压力。
E、球A的运动频率大于球B的运动频率。
第一步:1、研究对象为A、B。2、两球轨道平面是水平的;3、它们的圆心均在转轴上;4、它们的向心力均在各自的水平轨道平面内指向各自圆心。
第二步:小球A和B的受力分析如图。
θ
第三步:列方程。
(两球向心力相等)
AB
对下列作圆周运动的物体受力分析,并指出什么力(或什么
力在什么方向上的分力)提供向心力。
1、物体在水平方向的圆周运动。
mg
T
mg
T
mg
f
N
2、涉及摩擦力的圆周运动
f
o
T
f
r
o
设物体M和水平面保持相对静止。当ω具有最小值时, M有向圆心运动的趋势故水平面对M的摩擦力方向和指向圆心方向相反,且等于最大静摩擦力2 N。
当ω有最大值时, M有离开圆心的趋势,水平面对M的摩擦力的
方向指向圆心反向,大小也为2 N。
如图示,细绳一端系着质量为M=0.6kg的物体,静止
在水平面,另一端通过光滑小孔掉着质量为m=0.3kg
的物体,M的中点与圆孔距离为0.2m,并知M和水平
面的最大静摩擦力为2N,现使此平面绕中心轴线转动
问角速度在什么范围m会处于静止状态?g=10m/S2
弹簧测力套筒
转动手柄
长
槽
短
槽
小球
三层变速塔轮
标尺
挡板
弹簧测力套筒
(2)有一种叫“飞椅”的游乐项目,示意图如图14所示,长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘,转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ,不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.
2008年广东物理卷
二、运动模型的建立
