(核心素养)人教版数学八年级上册 15.3第1课时 分式方程及其解法 教案(表格式)
文档属性
| 名称 | (核心素养)人教版数学八年级上册 15.3第1课时 分式方程及其解法 教案(表格式) | 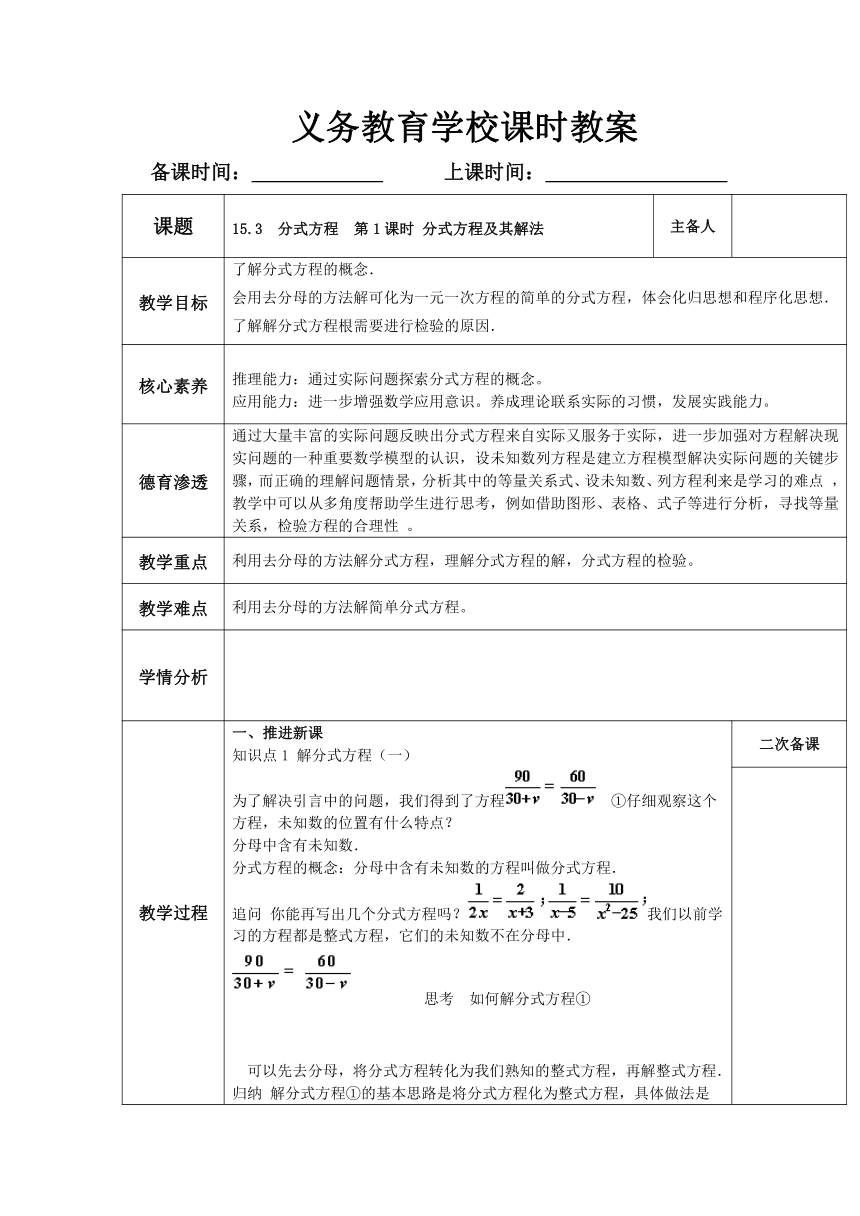 | |
| 格式 | doc | ||
| 文件大小 | 160.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-19 15:11:51 | ||
图片预览

文档简介
义务教育学校课时教案
备课时间: 上课时间:
课题 15.3 分式方程 第1课时 分式方程及其解法 主备人
教学目标 了解分式方程的概念.会用去分母的方法解可化为一元一次方程的简单的分式方程,体会化归思想和程序化思想.了解解分式方程根需要进行检验的原因.
核心素养 推理能力:通过实际问题探索分式方程的概念。应用能力:进一步增强数学应用意识。养成理论联系实际的习惯,发展实践能力。
德育渗透 通过大量丰富的实际问题反映出分式方程来自实际又服务于实际,进一步加强对方程解决现实问题的一种重要数学模型的认识,设未知数列方程是建立方程模型解决实际问题的关键步骤,而正确的理解问题情景,分析其中的等量关系式、设未知数、列方程利来是学习的难点 ,教学中可以从多角度帮助学生进行思考,例如借助图形、表格、式子等进行分析,寻找等量关系,检验方程的合理性 。
教学重点 利用去分母的方法解分式方程,理解分式方程的解,分式方程的检验。
教学难点 利用去分母的方法解简单分式方程。
学情分析
教学过程 一、推进新课知识点1 解分式方程(一)为了解决引言中的问题,我们得到了方程 ①仔细观察这个方程,未知数的位置有什么特点?分母中含有未知数.分式方程的概念:分母中含有未知数的方程叫做分式方程.追问 你能再写出几个分式方程吗?我们以前学习的方程都是整式方程,它们的未知数不在分母中.思考 如何解分式方程① 可以先去分母,将分式方程转化为我们熟知的整式方程,再解整式方程.归纳 解分式方程①的基本思路是将分式方程化为整式方程,具体做法是“去分母”,即方程两边乘最简公分母,这也是解分式方程的一般方法. 思考:以上分式方程的最简公分母是什么?二. 强化练习练习1下列方程哪些是分式方程练习2 指出下列方程中各分母的最简公分母 例题讲解例1解方程解:方程两边乘x(x-3),得2x=3x-9 X=9检验:当x=9时,所以,x=9是原分式方程的解. 练习3 解分式方程 知识点2 解分式方程(二)思考 上面两个分式方程中,为什么 ①去分母后所得整式方程的解就是①的解,而②去分母后所得整式方程的解却不是②的解呢?解分式方程去分母时,方程两边要乘同一个含未知数的式子(最简公分母). 一般地,解分式方程时,去分母后所得整式方程的解有可能使原方程中分母为0,因此应做如下检验:将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原方程的解;否则这个解不是原方程的解. 四.课堂小结 二次备课
板书设计 15.3 分式方程 第1课时 分式方程及其解法定义 例题 练习
作业设计与布置 作业类型 作业内容 试做时长
基础性作业 基本性作业(必做) 同步练习册基础练习 5分钟
鼓励性作业(选择) 同步练习册综合提升 5分钟
挑战性作业(选择) 同步练习册创新应用 5分钟
拓展性作业
作业反馈记录
教学反思
备课组长审核签字 教研组长审核签字 年级部审核签字 党支部审核签字
时间 时间 时间 时间
备课时间: 上课时间:
课题 15.3 分式方程 第1课时 分式方程及其解法 主备人
教学目标 了解分式方程的概念.会用去分母的方法解可化为一元一次方程的简单的分式方程,体会化归思想和程序化思想.了解解分式方程根需要进行检验的原因.
核心素养 推理能力:通过实际问题探索分式方程的概念。应用能力:进一步增强数学应用意识。养成理论联系实际的习惯,发展实践能力。
德育渗透 通过大量丰富的实际问题反映出分式方程来自实际又服务于实际,进一步加强对方程解决现实问题的一种重要数学模型的认识,设未知数列方程是建立方程模型解决实际问题的关键步骤,而正确的理解问题情景,分析其中的等量关系式、设未知数、列方程利来是学习的难点 ,教学中可以从多角度帮助学生进行思考,例如借助图形、表格、式子等进行分析,寻找等量关系,检验方程的合理性 。
教学重点 利用去分母的方法解分式方程,理解分式方程的解,分式方程的检验。
教学难点 利用去分母的方法解简单分式方程。
学情分析
教学过程 一、推进新课知识点1 解分式方程(一)为了解决引言中的问题,我们得到了方程 ①仔细观察这个方程,未知数的位置有什么特点?分母中含有未知数.分式方程的概念:分母中含有未知数的方程叫做分式方程.追问 你能再写出几个分式方程吗?我们以前学习的方程都是整式方程,它们的未知数不在分母中.思考 如何解分式方程① 可以先去分母,将分式方程转化为我们熟知的整式方程,再解整式方程.归纳 解分式方程①的基本思路是将分式方程化为整式方程,具体做法是“去分母”,即方程两边乘最简公分母,这也是解分式方程的一般方法. 思考:以上分式方程的最简公分母是什么?二. 强化练习练习1下列方程哪些是分式方程练习2 指出下列方程中各分母的最简公分母 例题讲解例1解方程解:方程两边乘x(x-3),得2x=3x-9 X=9检验:当x=9时,所以,x=9是原分式方程的解. 练习3 解分式方程 知识点2 解分式方程(二)思考 上面两个分式方程中,为什么 ①去分母后所得整式方程的解就是①的解,而②去分母后所得整式方程的解却不是②的解呢?解分式方程去分母时,方程两边要乘同一个含未知数的式子(最简公分母). 一般地,解分式方程时,去分母后所得整式方程的解有可能使原方程中分母为0,因此应做如下检验:将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原方程的解;否则这个解不是原方程的解. 四.课堂小结 二次备课
板书设计 15.3 分式方程 第1课时 分式方程及其解法定义 例题 练习
作业设计与布置 作业类型 作业内容 试做时长
基础性作业 基本性作业(必做) 同步练习册基础练习 5分钟
鼓励性作业(选择) 同步练习册综合提升 5分钟
挑战性作业(选择) 同步练习册创新应用 5分钟
拓展性作业
作业反馈记录
教学反思
备课组长审核签字 教研组长审核签字 年级部审核签字 党支部审核签字
时间 时间 时间 时间
