1.2 进制与进制转换 课件(共25张PPT) 高中信息技术粤教版(2019)必修1
文档属性
| 名称 | 1.2 进制与进制转换 课件(共25张PPT) 高中信息技术粤教版(2019)必修1 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2024-09-19 11:06:46 | ||
图片预览


文档简介
(共25张PPT)
粤教版普通高中教科书
信息技术 必修1
进制与进制转换
灵璧县第二中学 王凤龙
——1.2数据编码先导课
进制与进制转换
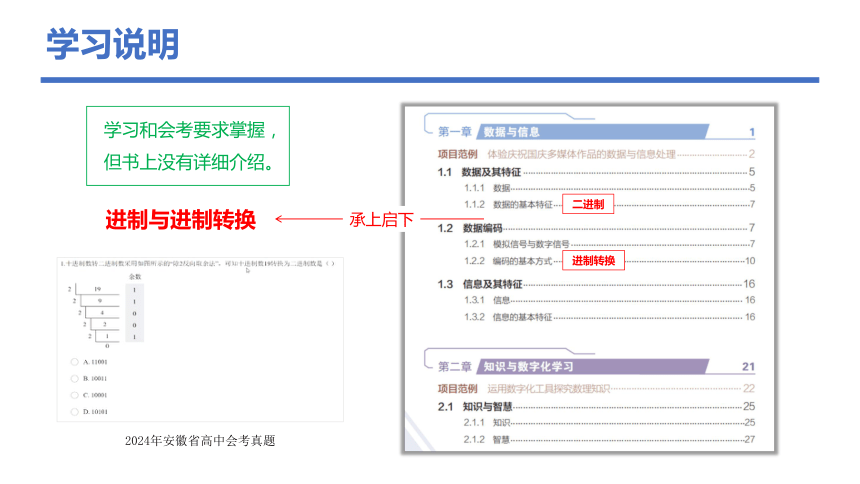
学习说明
二进制
进制转换
承上启下
学习和会考要求掌握,
但书上没有详细介绍。
2024年安徽省高中会考真题
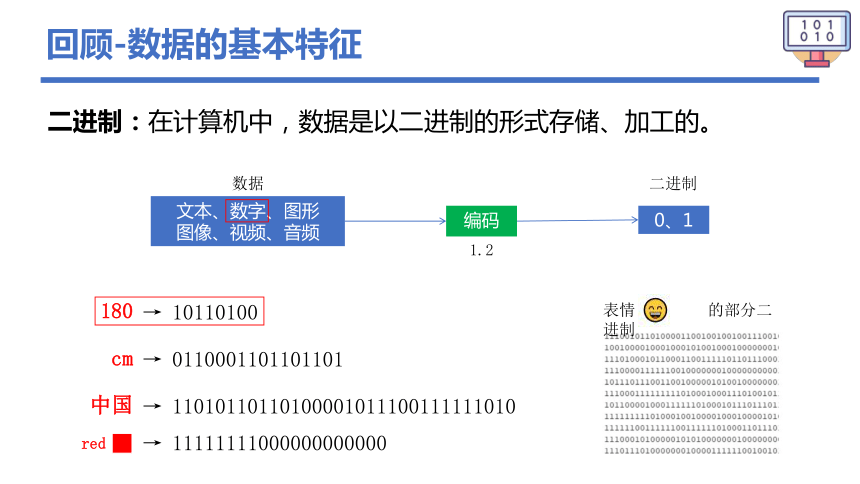
回顾-数据的基本特征
二进制:在计算机中,数据是以二进制的形式存储、加工的。
文本、数字、图形
图像、视频、音频
编码
0、1
数据
二进制
表情 的部分二进制
180
10110100
→
cm
0110001101101101
→
中国
11010110110100001011100111111010
→
→
11111111000000000000
red
1.2
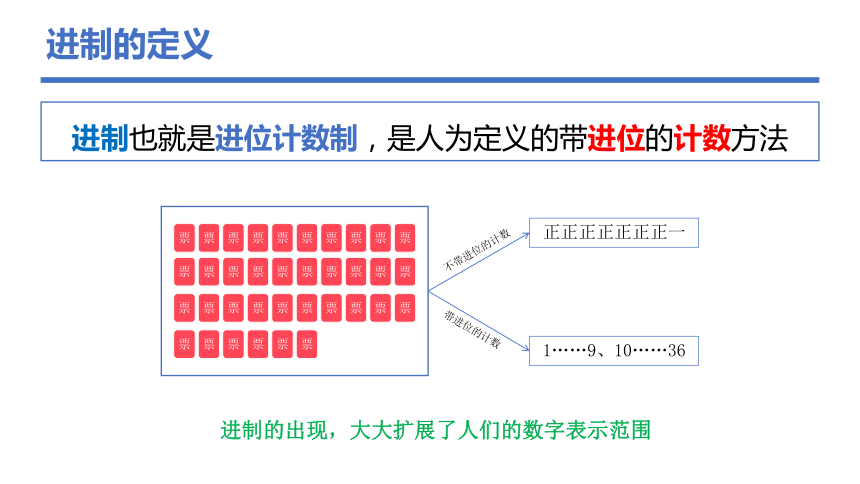
进制的定义
进制也就是进位计数制,是人为定义的带进位的计数方法
正正正正正正正一
1……9、10……36
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
不带进位的计数
带进位的计数
进制的出现,大大扩展了人们的数字表示范围
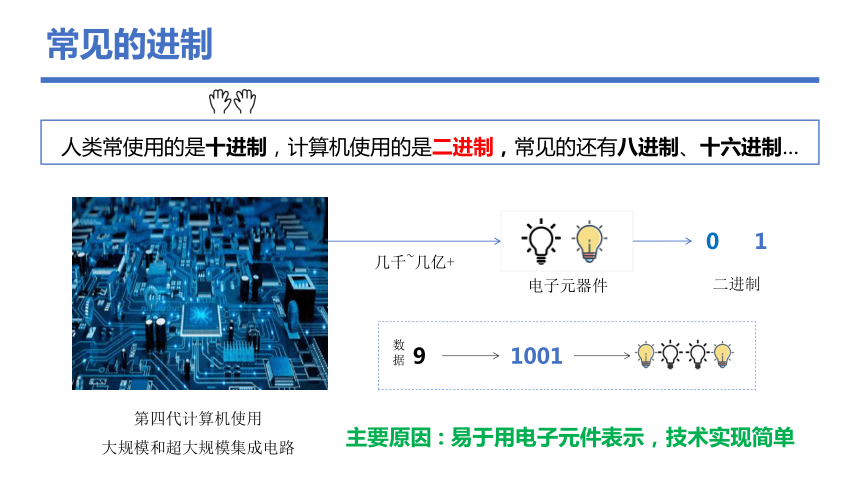
常见的进制
人类常使用的是十进制,计算机使用的是二进制,常见的还有八进制、十六进制…
第四代计算机使用
大规模和超大规模集成电路
几千~几亿+
电子元器件
1
0
二进制
1001
9
数据
主要原因 : 易于用电子元件表示,技术实现简单
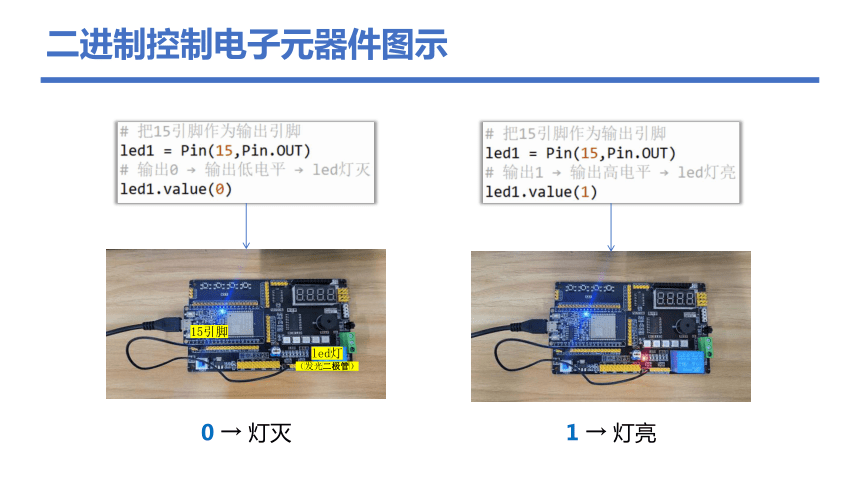
二进制控制电子元器件图示
0 → 灯灭
1 → 灯亮
15引脚
led灯
(发光二极管)
进制的运算规则
对于任何一种进制---x进制,就表示每一位上的数运算时都是逢x进一位。十进制是逢十进一,二进制就是逢二进一,以此类推,x进制就是逢x进一。
十进制运算
2 3
4 7
————
+
1
二进制运算
1
1
————
+
1 0
1
+
1 7
2 2
————
4 1
1
八进制运算
101+101 = ?
1010
7 0
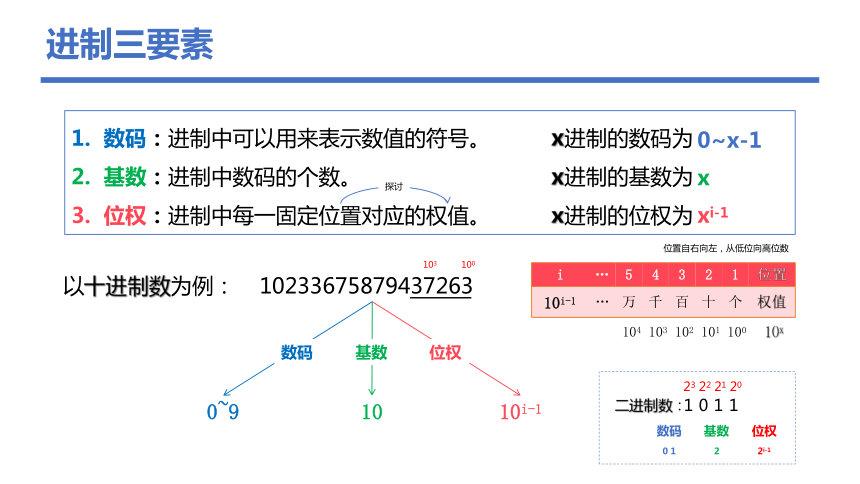
进制三要素
以十进制数为例:
数码:进制中可以用来表示数值的符号。
基数:进制中数码的个数。
位权:进制中每一固定位置对应的权值。
x进制的数码为
x进制的基数为
x进制的位权为
10233675879437263
0~9
10
10i-1
数码
基数
位权
位置自右向左,从低位向高位数
20
21
22
23
0 1
1011
二进制数:
数码
位权
基数
2
2i-1
i … 5 4 3 2 1 位置
… 万 千 百 十 个 权值
10i-1
100
101
102
103
104
10x
100
103
探讨
0~x-1
x
xi-1
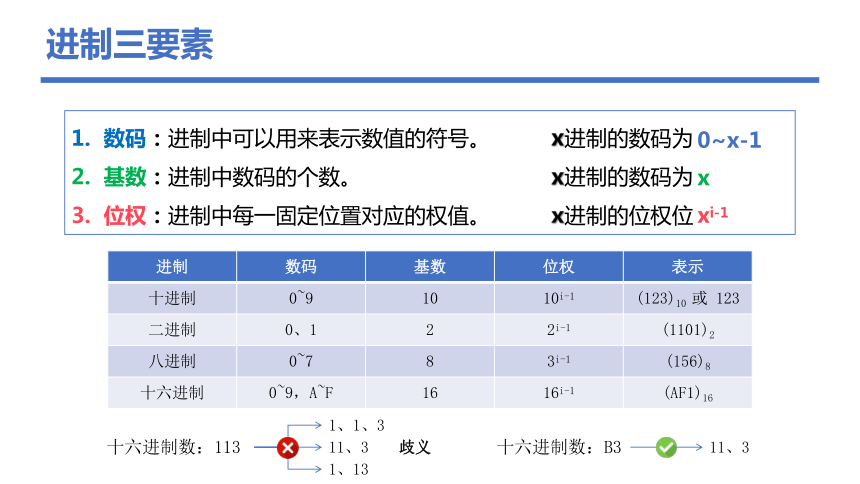
进制三要素
数码:进制中可以用来表示数值的符号。
基数:进制中数码的个数。
位权:进制中每一固定位置对应的权值。
x进制的数码为
x进制的数码为
x进制的位权位
进制 数码 基数 位权 表示
十进制 0~9 10 10i-1 (123)10 或 123
二进制 0、1 2 2i-1 (1101)2
八进制 0~7 8 3i-1 (156)8
十六进制 0~9,A~F 16 16i-1 (AF1)16
十六进制数:113
1、1、3
11、3
1、13
歧义
十六进制数:B3
11、3
0~x-1
x
xi-1
进制的转换
1001
9
数据
十进制
八进制
二进制
十六进制
四分法
三分法
除基反向取余法
按位权展开相加法
重点
二进制与十进制的相互转换是每年会考的常考点,其他仅做了解,不要求掌握
其他进制转十进制(按位权展开相加法)
八进制、十六进制同上
将其他进制数自右向左按位权展开,然后将其每一数位的值与对应的位权相乘,最后将这些乘积相加即可。
下面以二进制转十进制为例:
( 11010 ) 2
20
21
22
23
24
0 + 2 + 0 + 8 + 16
=
=
26
=
1×24
1×23
0×22
1×21
0×20
+
+
+
+
(11010)2 =
x进制的位权为xi-1
其他进制转十进制 (按位权展开相加法)
参考下表,将下列二进制转换为十进制:
28 27 26 25 24 23 22 21 20
256 128 64 32 16 8 4 2 1
① ( 1101 ) 2 =
② ( 101001 ) 2 =
③ ( 10110011) 2 =
1×20 + 0×21 + 1×22 + 1×23 = 1 + 0 + 4 + 8 = 13
1×20 + 1×23 + 1×25 = 1 + 8 + 32 = 41
21
20
22
23
21
20
22
23
24
25
1+ 2 + 16 + 32 + 128 = 179
21
20
22
23
24
25
26
27
十进制转其他进制 (除基反向取余法)
将十进制整数除以基数,得到商数和余数,用商数再除以基数,依此类推直到商数为0为止,将每次得到的余数按照逆序排列即可。
下面以十进制转二进制为例:
八进制、十六进制同上
(19)10 =
10011
20
21
22
23
24
= 1×20+1×21+0×22+0×23+1×24
= 1 + 2 + 0 + 0 + 16
= 19
1÷2 = 0……1
÷
……
=
参考图例,将下列十进制转换为二进制:
十进制转其他进制 (除基反向取余法)
( 6 ) 10
( 22) 10
图例
2
6
2
3
2
1
0
1
1
0
110
0
0
1
1
0
1
2
22
2
11
2
5
2
2
2
1
10110
三分法、四分法
二进制与八进制的相互转换、二进制与十六进制的相互转换
仅做了解,不要求掌握
二进制与八进制的相互转换(三分法)
八进制的数码范围是 0 到 7 ;
三位二进制能表示的最小二进制数是 000 B,对应十进制数是 0 ;
三位二进制能表示的最大二进制数是 111 B,对应十进制数是 7 。
因此使用3位二进制数可以表示任意1位八进制数,反之任意1位八进制数都可以使用3位二进制数表示。
二进制 八进制
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7
二进制
八进制
3合1
1拆3
三分法
二进制与八进制的相互转换(三分法)
二进制 八进制
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7
二进制
八进制
3合1
1拆3
三分法
二转八:
八转二:
(101011)2 = 101,011 = (53)8
(11010)2 = 011,010 = (32)8
(57)8 = 101,111 = (101111)2
(34)8 = 011,100 = (11100)2
在二进制数前方添加或减少任意数量的0不会影响结果
二进制与十六进制的相互转换(四分法)
十六进制的数码范围是 0 到 15 ;
三位二进制能表示的最小二进制数是 0000 B,对应十进制数是 0 ;
三位二进制能表示的最大二进制数是 1111 B,对应十进制数是 15 。
二进制
十六进制
4合1
1拆4
四分法
因此使用4位二进制数可以表示任意1位十六进制数,反之任意1位十六进制数都可以使用4位二进制数表示。
二进制 十六进制
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 A (10)
1011 B (11)
1100 C (12)
1101 D (13)
1110 E (14)
1111 F (15)
二进制与八进制的相互转换(四分法)
二转八:
八转二:
(10011011)2 = 1001,1011 = (9B)16
(110001)2 = 0011,0001 = (31)16
(87)16 = 1000,0111= (10000111)2
(2A)16 = 0010,1010 = (101010)2
在二进制数前方添加或减少任意数量的0不会影响结果
二进制
十六进制
4合1
1拆4
四分法
二进制 十六进制
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 A (10)
1011 B (11)
1100 C (12)
1101 D (13)
1110 E (14)
1111 F (15)
总结
十进制
八进制
二进制
十六进制
四分法
三分法
除基反向取余法
按位权展开相加法
重点
真题练习(1/2)
A. 二
B. 八
C. 十
D. 十六
1、在计算机中,数据以 ( ) 进制的形式存储、加工
A. 101110101
B. 111110101
C. 010001010
D. 000001010
2、图1是一张磁卡通过刷卡时显示的波形,已知该波形所表示的二进制代码为100101110据此判断,图2中的波形表示的二进制代码是 ( )
A
1
0
A
3、参考表1,求( 1011 )2转换为十进制的结果是 ( )
真题练习(2/2)
C
A. 9
B. 10
C. 11
D. 12
A. 1011
B. 1101
C. 1010
D. 0101
4、参考图1,求( 13 )10 转换为二进制的结果是 ( )
B
23 22 21 20
8 4 2 1
图1
表1
拓展:利用电脑自带的计算器进行进制转换
电脑搜索打开“计算器”
选择“程序员”模式
进行进制转换
①
②
作业
位数 可表示的二进制数 个数
1 0、1 2
2 00、01、10、11 4
3 000、001、010、011 100、101、110、111 8
n …… ?
思考:n个二进制位可以表示多少种不同的二进制数呢?
分析出“二进制位数与其可表示的不同二进制个数之间的关系”
本节课到此结束
粤教版普通高中教科书
信息技术 必修1
进制与进制转换
灵璧县第二中学 王凤龙
——1.2数据编码先导课
进制与进制转换
学习说明
二进制
进制转换
承上启下
学习和会考要求掌握,
但书上没有详细介绍。
2024年安徽省高中会考真题
回顾-数据的基本特征
二进制:在计算机中,数据是以二进制的形式存储、加工的。
文本、数字、图形
图像、视频、音频
编码
0、1
数据
二进制
表情 的部分二进制
180
10110100
→
cm
0110001101101101
→
中国
11010110110100001011100111111010
→
→
11111111000000000000
red
1.2
进制的定义
进制也就是进位计数制,是人为定义的带进位的计数方法
正正正正正正正一
1……9、10……36
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
票
不带进位的计数
带进位的计数
进制的出现,大大扩展了人们的数字表示范围
常见的进制
人类常使用的是十进制,计算机使用的是二进制,常见的还有八进制、十六进制…
第四代计算机使用
大规模和超大规模集成电路
几千~几亿+
电子元器件
1
0
二进制
1001
9
数据
主要原因 : 易于用电子元件表示,技术实现简单
二进制控制电子元器件图示
0 → 灯灭
1 → 灯亮
15引脚
led灯
(发光二极管)
进制的运算规则
对于任何一种进制---x进制,就表示每一位上的数运算时都是逢x进一位。十进制是逢十进一,二进制就是逢二进一,以此类推,x进制就是逢x进一。
十进制运算
2 3
4 7
————
+
1
二进制运算
1
1
————
+
1 0
1
+
1 7
2 2
————
4 1
1
八进制运算
101+101 = ?
1010
7 0
进制三要素
以十进制数为例:
数码:进制中可以用来表示数值的符号。
基数:进制中数码的个数。
位权:进制中每一固定位置对应的权值。
x进制的数码为
x进制的基数为
x进制的位权为
10233675879437263
0~9
10
10i-1
数码
基数
位权
位置自右向左,从低位向高位数
20
21
22
23
0 1
1011
二进制数:
数码
位权
基数
2
2i-1
i … 5 4 3 2 1 位置
… 万 千 百 十 个 权值
10i-1
100
101
102
103
104
10x
100
103
探讨
0~x-1
x
xi-1
进制三要素
数码:进制中可以用来表示数值的符号。
基数:进制中数码的个数。
位权:进制中每一固定位置对应的权值。
x进制的数码为
x进制的数码为
x进制的位权位
进制 数码 基数 位权 表示
十进制 0~9 10 10i-1 (123)10 或 123
二进制 0、1 2 2i-1 (1101)2
八进制 0~7 8 3i-1 (156)8
十六进制 0~9,A~F 16 16i-1 (AF1)16
十六进制数:113
1、1、3
11、3
1、13
歧义
十六进制数:B3
11、3
0~x-1
x
xi-1
进制的转换
1001
9
数据
十进制
八进制
二进制
十六进制
四分法
三分法
除基反向取余法
按位权展开相加法
重点
二进制与十进制的相互转换是每年会考的常考点,其他仅做了解,不要求掌握
其他进制转十进制(按位权展开相加法)
八进制、十六进制同上
将其他进制数自右向左按位权展开,然后将其每一数位的值与对应的位权相乘,最后将这些乘积相加即可。
下面以二进制转十进制为例:
( 11010 ) 2
20
21
22
23
24
0 + 2 + 0 + 8 + 16
=
=
26
=
1×24
1×23
0×22
1×21
0×20
+
+
+
+
(11010)2 =
x进制的位权为xi-1
其他进制转十进制 (按位权展开相加法)
参考下表,将下列二进制转换为十进制:
28 27 26 25 24 23 22 21 20
256 128 64 32 16 8 4 2 1
① ( 1101 ) 2 =
② ( 101001 ) 2 =
③ ( 10110011) 2 =
1×20 + 0×21 + 1×22 + 1×23 = 1 + 0 + 4 + 8 = 13
1×20 + 1×23 + 1×25 = 1 + 8 + 32 = 41
21
20
22
23
21
20
22
23
24
25
1+ 2 + 16 + 32 + 128 = 179
21
20
22
23
24
25
26
27
十进制转其他进制 (除基反向取余法)
将十进制整数除以基数,得到商数和余数,用商数再除以基数,依此类推直到商数为0为止,将每次得到的余数按照逆序排列即可。
下面以十进制转二进制为例:
八进制、十六进制同上
(19)10 =
10011
20
21
22
23
24
= 1×20+1×21+0×22+0×23+1×24
= 1 + 2 + 0 + 0 + 16
= 19
1÷2 = 0……1
÷
……
=
参考图例,将下列十进制转换为二进制:
十进制转其他进制 (除基反向取余法)
( 6 ) 10
( 22) 10
图例
2
6
2
3
2
1
0
1
1
0
110
0
0
1
1
0
1
2
22
2
11
2
5
2
2
2
1
10110
三分法、四分法
二进制与八进制的相互转换、二进制与十六进制的相互转换
仅做了解,不要求掌握
二进制与八进制的相互转换(三分法)
八进制的数码范围是 0 到 7 ;
三位二进制能表示的最小二进制数是 000 B,对应十进制数是 0 ;
三位二进制能表示的最大二进制数是 111 B,对应十进制数是 7 。
因此使用3位二进制数可以表示任意1位八进制数,反之任意1位八进制数都可以使用3位二进制数表示。
二进制 八进制
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7
二进制
八进制
3合1
1拆3
三分法
二进制与八进制的相互转换(三分法)
二进制 八进制
000 0
001 1
010 2
011 3
100 4
101 5
110 6
111 7
二进制
八进制
3合1
1拆3
三分法
二转八:
八转二:
(101011)2 = 101,011 = (53)8
(11010)2 = 011,010 = (32)8
(57)8 = 101,111 = (101111)2
(34)8 = 011,100 = (11100)2
在二进制数前方添加或减少任意数量的0不会影响结果
二进制与十六进制的相互转换(四分法)
十六进制的数码范围是 0 到 15 ;
三位二进制能表示的最小二进制数是 0000 B,对应十进制数是 0 ;
三位二进制能表示的最大二进制数是 1111 B,对应十进制数是 15 。
二进制
十六进制
4合1
1拆4
四分法
因此使用4位二进制数可以表示任意1位十六进制数,反之任意1位十六进制数都可以使用4位二进制数表示。
二进制 十六进制
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 A (10)
1011 B (11)
1100 C (12)
1101 D (13)
1110 E (14)
1111 F (15)
二进制与八进制的相互转换(四分法)
二转八:
八转二:
(10011011)2 = 1001,1011 = (9B)16
(110001)2 = 0011,0001 = (31)16
(87)16 = 1000,0111= (10000111)2
(2A)16 = 0010,1010 = (101010)2
在二进制数前方添加或减少任意数量的0不会影响结果
二进制
十六进制
4合1
1拆4
四分法
二进制 十六进制
0000 0
0001 1
0010 2
0011 3
0100 4
0101 5
0110 6
0111 7
1000 8
1001 9
1010 A (10)
1011 B (11)
1100 C (12)
1101 D (13)
1110 E (14)
1111 F (15)
总结
十进制
八进制
二进制
十六进制
四分法
三分法
除基反向取余法
按位权展开相加法
重点
真题练习(1/2)
A. 二
B. 八
C. 十
D. 十六
1、在计算机中,数据以 ( ) 进制的形式存储、加工
A. 101110101
B. 111110101
C. 010001010
D. 000001010
2、图1是一张磁卡通过刷卡时显示的波形,已知该波形所表示的二进制代码为100101110据此判断,图2中的波形表示的二进制代码是 ( )
A
1
0
A
3、参考表1,求( 1011 )2转换为十进制的结果是 ( )
真题练习(2/2)
C
A. 9
B. 10
C. 11
D. 12
A. 1011
B. 1101
C. 1010
D. 0101
4、参考图1,求( 13 )10 转换为二进制的结果是 ( )
B
23 22 21 20
8 4 2 1
图1
表1
拓展:利用电脑自带的计算器进行进制转换
电脑搜索打开“计算器”
选择“程序员”模式
进行进制转换
①
②
作业
位数 可表示的二进制数 个数
1 0、1 2
2 00、01、10、11 4
3 000、001、010、011 100、101、110、111 8
n …… ?
思考:n个二进制位可以表示多少种不同的二进制数呢?
分析出“二进制位数与其可表示的不同二进制个数之间的关系”
本节课到此结束
同课章节目录
- 第一章 数据与信息
- 项目范例 体验庆祝国庆多媒体作品的数据与信息处理
- 1.1 数据及其特征
- 1.2 数据编码
- 1.3 信息及其特征
- 第二章 知识与数字化学习
- 项目范例 运用数字化工具探究数理知识
- 2.1 知识与智慧
- 2.2 数字化学习与创新
- 第三章 算法基础
- 项目范例 设计从A市到B市耗时最少的旅行路线方案
- 3.1 体验计算机解决问题的过程
- 3.2 算法及其描述
- 3.3 计算机程序与程序设计语言
- 第四章 程序设计基础
- 项目范例 设计购买纪念品的最佳方案
- 4.1 程序设计语言的基础知识
- 4.2 运用顺序结构描述问题求解过程
- 4.3 运用选择结构描述问题求解过程
- 4.4 运用循环结构描述问题求解过程
- 第五章 数据处理和可视化表达
- 项目范例 网络购物平台客户行为数据分析和可视化表达
- 5.1 认识大数据
- 5.2 数据的采集
- 5.3 数据的分析
- 5.4 数据的可视化表达
- 第六章 人工智能及其应用
- 项目范例 剖析空调企业智能客服机器人
- 6.1 认识人工智能
- 6.2 人工智能的应用
