2024-2025学年河南省开封市杞县高中宏志班高二(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年河南省开封市杞县高中宏志班高二(上)开学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 90.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-19 00:00:00 | ||
图片预览



文档简介
2024-2025学年河南省开封市杞县高中宏志班高二(上)开学
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数,则( )
A. B. C. D.
2.在中,角,,的对边分别为,,,已知,,则( )
A. B. C. D.
3.已知,是两条不同的直线,,,是三个不同的平面,下列命题正确的是( )
A. 若,,,则 B. 若,,则
C. 若,,,则 D. 若,,则
4.向量与的夹角为( )
A. B. C. D.
5.数据,,,,,,的第百分位数是( )
A. B. C. D.
6.已知两条不同的直线,和两个不同的平面,,下列四个命题中正确的为( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
7.某学校高一年级学生有人,其中男生人,女生人,为了获得该校高一全生的身高信息,现采用样本量按比例分配的分层随机抽样方法抽取了容量为的样本计算得男生样本的均值为,女生样本的均值为,则抽取的样本的均值为是( )
A. B. C. D.
8.在如图所示的电路中,三个开关,,闭合与否相互独立,且在某一时刻,,闭合的概率分别为,,,则此时灯亮的概率为( )
A. B.
C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知向量,满足,则以下说法正确的是( )
A. 若,,则或
B. 若,则
C. 若,,则向量在向量上的投影数量为
D. 向量在向量上的投影向量为
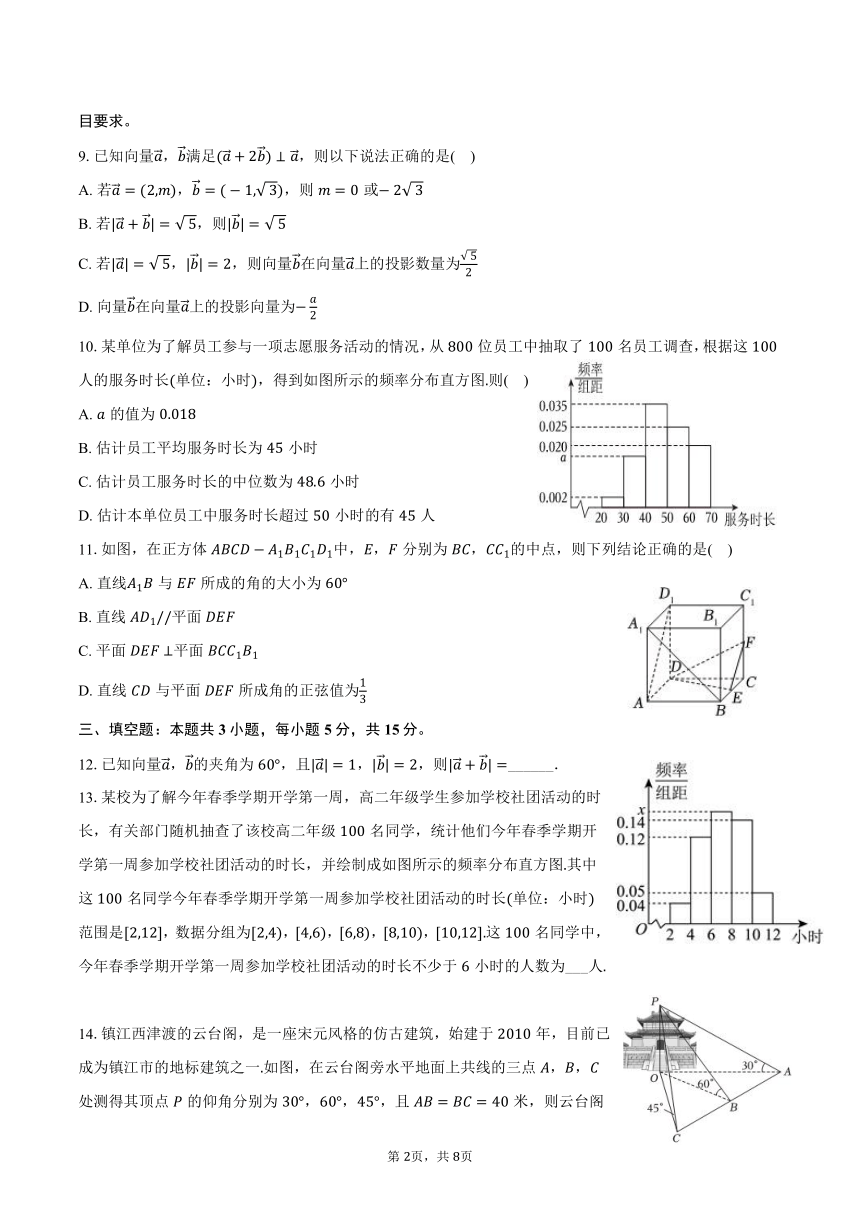
10.某单位为了解员工参与一项志愿服务活动的情况,从位员工中抽取了名员工调查,根据这人的服务时长单位:小时,得到如图所示的频率分布直方图则( )
A. 的值为
B. 估计员工平均服务时长为小时
C. 估计员工服务时长的中位数为小时
D. 估计本单位员工中服务时长超过小时的有人
11.如图,在正方体中,,分别为,的中点,则下列结论正确的是( )
A. 直线与所成的角的大小为
B. 直线平面
C. 平面平面
D. 直线与平面所成角的正弦值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量,的夹角为,且,,则______.
13.某校为了解今年春季学期开学第一周,高二年级学生参加学校社团活动的时长,有关部门随机抽查了该校高二年级名同学,统计他们今年春季学期开学第一周参加学校社团活动的时长,并绘制成如图所示的频率分布直方图其中这名同学今年春季学期开学第一周参加学校社团活动的时长单位:小时范围是,数据分组为,,,,这名同学中,今年春季学期开学第一周参加学校社团活动的时长不少于小时的人数为___人
14.镇江西津渡的云台阁,是一座宋元风格的仿古建筑,始建于年,目前已成为镇江市的地标建筑之一如图,在云台阁旁水平地面上共线的三点,,处测得其顶点的仰角分别为,,,且米,则云台阁的高度为______米
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知平面向量,.
若,求;
若,求.
16.本小题分
已知,,分别为三个内角,,的对边,.
若,,求;
若,求周长的最大值.
17.本小题分
某消防队为了了解市民对“消防基本常识”的认知程度,针对本市不同年龄的人举办了一次“消防之星”知识竞赛,满分分分及以上为“消防之星”,共有人荣获“消防之星”称号,将其按年龄分成以下五组:第一组,第二组,第三组,第四组,第五组,得到如图所示的频率分布直方图.
根据频率分布直方图,估计这些人的平均年龄和第百分位数;
若从第三组,第四组,第五组三组中分层抽取人,再从这人中随机抽取人,求抽取的人年龄在不同组的概率;
若第三组的年龄的平均数与方差分别为和,第四组的年龄的平均数与方差分别为和,据此计算这人中第三组与第四组所有人的年龄的方差.
附:
18.本小题分
如图,直三棱柱中,与交于点,为线段的中点,,.
求证:平面;
求证:平面平面;
求三棱锥的体积.
19.本小题分
如图,在四棱锥中,侧棱底面,四边形为正方形,且,点为棱的中点,点为棱上一点.
若点为中点,求证:平面;
若点满足,
求证:;
求直线与平面所成角的正切值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:平面向量,,
因为,所以,解得,所以;
所以;
因为,解得;
所以,,
所以,.
16.解:,,,
则,即,
,
则;
,,
则,解得,当且仅当时,等号成立,
故周长的最大值为.
17.解:估计这些人的平均年龄为:
岁;
,,
估计这些人的第百分位数为:
岁;
第三组,第四组,第五组的频率之比为:::::,
抽取的人依次为人;人;人,分别依次设为,,;,;,
则再从这人中随机抽取人所得样本空间为:
,,,,,,,,,,,,,,,
设“抽取的人年龄在不同组“,
则,,,,,,,,,,,
;
第三组与第四组的频率之比为::,
第三组与第四组的加权平均数为:,
第三组与第四组的加权方差为.
18.解:证明:连接,因为直三棱柱,
,,又,
是正方形且为线段的中点,
又为线段中点,
,
又平面,平面,
平面;
证明:,,,
平面,
又平面,
平面平面;
为线段中点,
,
即三棱锥的体积为.
19.解:证明:中,点,分别为棱,的中点,
,
又四边形是正方形,
,
,
又平面,平面,
平面;
证明:在四棱锥中,
平面,四边形为正方形,
则,,且,平面,平面,
平面,又平面,
,
又在三角形中,,为的中点,
,
又,,
平面,平面,
平面,又平面,
,又,,平面,平面,
平面,又平面,
;
由可知即为直线与平面所成的角,
在中,,,
则,
又,,
,
故直线与平面所成的角的正切值为.
第1页,共1页
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知复数,则( )
A. B. C. D.
2.在中,角,,的对边分别为,,,已知,,则( )
A. B. C. D.
3.已知,是两条不同的直线,,,是三个不同的平面,下列命题正确的是( )
A. 若,,,则 B. 若,,则
C. 若,,,则 D. 若,,则
4.向量与的夹角为( )
A. B. C. D.
5.数据,,,,,,的第百分位数是( )
A. B. C. D.
6.已知两条不同的直线,和两个不同的平面,,下列四个命题中正确的为( )
A. 若,,则 B. 若,,则
C. 若,,则 D. 若,,则
7.某学校高一年级学生有人,其中男生人,女生人,为了获得该校高一全生的身高信息,现采用样本量按比例分配的分层随机抽样方法抽取了容量为的样本计算得男生样本的均值为,女生样本的均值为,则抽取的样本的均值为是( )
A. B. C. D.
8.在如图所示的电路中,三个开关,,闭合与否相互独立,且在某一时刻,,闭合的概率分别为,,,则此时灯亮的概率为( )
A. B.
C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知向量,满足,则以下说法正确的是( )
A. 若,,则或
B. 若,则
C. 若,,则向量在向量上的投影数量为
D. 向量在向量上的投影向量为
10.某单位为了解员工参与一项志愿服务活动的情况,从位员工中抽取了名员工调查,根据这人的服务时长单位:小时,得到如图所示的频率分布直方图则( )
A. 的值为
B. 估计员工平均服务时长为小时
C. 估计员工服务时长的中位数为小时
D. 估计本单位员工中服务时长超过小时的有人
11.如图,在正方体中,,分别为,的中点,则下列结论正确的是( )
A. 直线与所成的角的大小为
B. 直线平面
C. 平面平面
D. 直线与平面所成角的正弦值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量,的夹角为,且,,则______.
13.某校为了解今年春季学期开学第一周,高二年级学生参加学校社团活动的时长,有关部门随机抽查了该校高二年级名同学,统计他们今年春季学期开学第一周参加学校社团活动的时长,并绘制成如图所示的频率分布直方图其中这名同学今年春季学期开学第一周参加学校社团活动的时长单位:小时范围是,数据分组为,,,,这名同学中,今年春季学期开学第一周参加学校社团活动的时长不少于小时的人数为___人
14.镇江西津渡的云台阁,是一座宋元风格的仿古建筑,始建于年,目前已成为镇江市的地标建筑之一如图,在云台阁旁水平地面上共线的三点,,处测得其顶点的仰角分别为,,,且米,则云台阁的高度为______米
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知平面向量,.
若,求;
若,求.
16.本小题分
已知,,分别为三个内角,,的对边,.
若,,求;
若,求周长的最大值.
17.本小题分
某消防队为了了解市民对“消防基本常识”的认知程度,针对本市不同年龄的人举办了一次“消防之星”知识竞赛,满分分分及以上为“消防之星”,共有人荣获“消防之星”称号,将其按年龄分成以下五组:第一组,第二组,第三组,第四组,第五组,得到如图所示的频率分布直方图.
根据频率分布直方图,估计这些人的平均年龄和第百分位数;
若从第三组,第四组,第五组三组中分层抽取人,再从这人中随机抽取人,求抽取的人年龄在不同组的概率;
若第三组的年龄的平均数与方差分别为和,第四组的年龄的平均数与方差分别为和,据此计算这人中第三组与第四组所有人的年龄的方差.
附:
18.本小题分
如图,直三棱柱中,与交于点,为线段的中点,,.
求证:平面;
求证:平面平面;
求三棱锥的体积.
19.本小题分
如图,在四棱锥中,侧棱底面,四边形为正方形,且,点为棱的中点,点为棱上一点.
若点为中点,求证:平面;
若点满足,
求证:;
求直线与平面所成角的正切值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:平面向量,,
因为,所以,解得,所以;
所以;
因为,解得;
所以,,
所以,.
16.解:,,,
则,即,
,
则;
,,
则,解得,当且仅当时,等号成立,
故周长的最大值为.
17.解:估计这些人的平均年龄为:
岁;
,,
估计这些人的第百分位数为:
岁;
第三组,第四组,第五组的频率之比为:::::,
抽取的人依次为人;人;人,分别依次设为,,;,;,
则再从这人中随机抽取人所得样本空间为:
,,,,,,,,,,,,,,,
设“抽取的人年龄在不同组“,
则,,,,,,,,,,,
;
第三组与第四组的频率之比为::,
第三组与第四组的加权平均数为:,
第三组与第四组的加权方差为.
18.解:证明:连接,因为直三棱柱,
,,又,
是正方形且为线段的中点,
又为线段中点,
,
又平面,平面,
平面;
证明:,,,
平面,
又平面,
平面平面;
为线段中点,
,
即三棱锥的体积为.
19.解:证明:中,点,分别为棱,的中点,
,
又四边形是正方形,
,
,
又平面,平面,
平面;
证明:在四棱锥中,
平面,四边形为正方形,
则,,且,平面,平面,
平面,又平面,
,
又在三角形中,,为的中点,
,
又,,
平面,平面,
平面,又平面,
,又,,平面,平面,
平面,又平面,
;
由可知即为直线与平面所成的角,
在中,,,
则,
又,,
,
故直线与平面所成的角的正切值为.
第1页,共1页
同课章节目录
