鲁教五四学制:2024-2025年八年级第一学期上册数学第4章图形的平移与旋转检测题(含答案)
文档属性
| 名称 | 鲁教五四学制:2024-2025年八年级第一学期上册数学第4章图形的平移与旋转检测题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 536.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-19 21:28:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
八年级数学上第四章《图形的旋转与平移》单元测试题
班级 姓名 成绩
一、选择题(每小题4分,共48分)
1. 下列标志既是轴对称图形又是中心对称图形的是( ).
A. B. C. D.
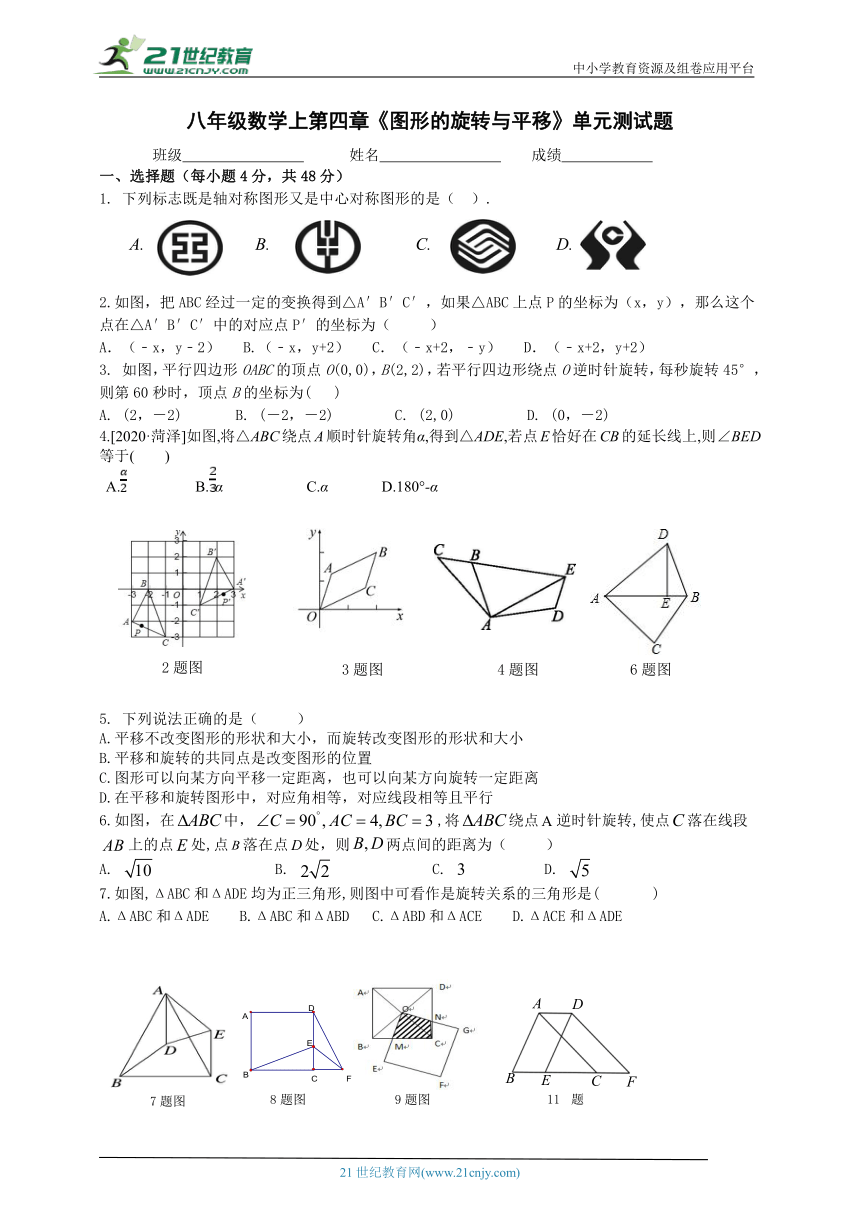
2.如图,把ABC经过一定的变换得到△A′B′C′,如果△ABC上点P的坐标为(x,y),那么这个点在△A′B′C′中的对应点P′的坐标为( )
(﹣x,y﹣2) B.(﹣x,y+2) C.(﹣x+2,﹣y) D.(﹣x+2,y+2)
3. 如图,平行四边形OABC的顶点O(0,0),B(2,2),若平行四边形绕点O逆时针旋转,每秒旋转45°,则第60秒时,顶点B的坐标为( )
A. (2,-2) B. (-2,-2) C. (2,0) D. (0,-2)
4.[2020·菏泽]如图,将△ABC绕点A顺时针旋转角α,得到△ADE,若点E恰好在CB的延长线上,则∠BED等于( )
A. B.α C.α D.180°-α
(
2
题图
)
3题图 4题图 6题图
5. 下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转改变图形的形状和大小
B.平移和旋转的共同点是改变图形的位置
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
6.如图,在中,,将绕点逆时针旋转,使点落在线段上的点处,点落在点处,则两点间的距离为( )
A. B. C. D.
7.如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( )
A.ΔABC和ΔADE B.ΔABC和ΔABD C.ΔABD和ΔACE D.ΔACE和ΔADE
(
D
) (
A
) (
9题图
) (
8题图
)
(
F
) (
E
) (
C
) (
B
) (
11题图
)
(
7题图
)
8.如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
A.100 B.150 C.200 D.250
9.如图,两个边长相等的两个正方形ABCD和OEFG,若将正方形OEFG绕 点O按逆时针
方向旋转150°,两个正方形的重叠部分四边形OMCN的面积( )
A.不变 B.先增大再减小 C.先减小再增大 D.不断增大
10.钟表2时15分,时针与分针的夹角为( )
A.30° B.45° C.22.5° D.15°
11.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
12. 将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
二、填空题(每小题4分,共24分)
13. 如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
(
16题图
) (
14题图
)
13题图 15题图
14.已知两个重合的正方形纸片,边长为4厘米,其中ABCD沿AB方向平移3厘米,平移后的两个正方形重叠部分的面积是 平方厘米.
15.如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是___________
16.如图,在一块长方形ABCD草地上,AB=10,BC=15,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2个单位),空白部分表示的草地面积是 .
17.直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,
则x+2y= .
18.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=_________.
三、解答题(78分) 18题图
(
.
.
.
.
.
A
B
C
E
F
)19.经过平移,△ABC的边AB移到了EF作出平移后的三角形.
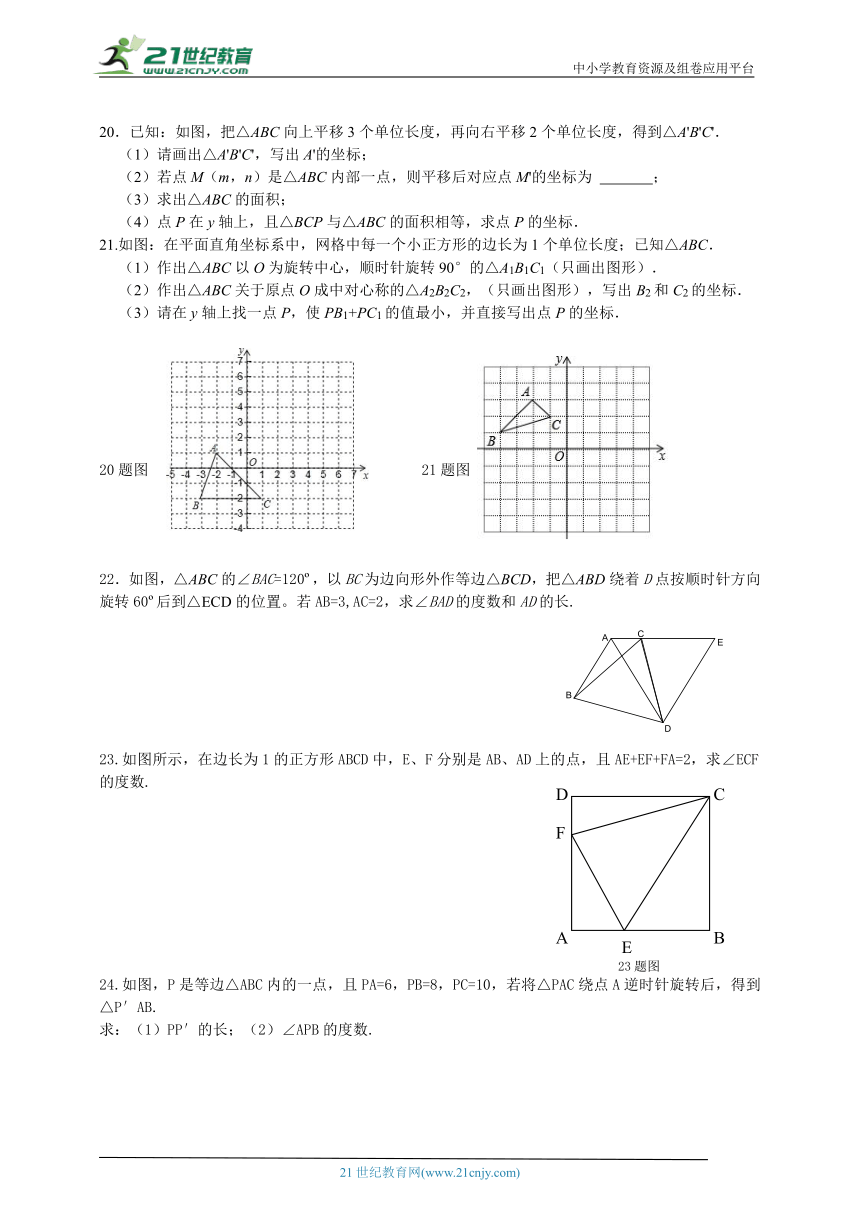
20.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'.
(1)请画出△A'B'C',写出A'的坐标;
(2)若点M(m,n)是△ABC内部一点,则平移后对应点M'的坐标为 ;
(3)求出△ABC的面积;
(4)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
21.如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1(只画出图形).
(2)作出△ABC关于原点O成中对心称的△A2B2C2,(只画出图形),写出B2和C2的坐标.
(3)请在y轴上找一点P,使PB1+PC1的值最小,并直接写出点P的坐标.
20题图 21题图
22.如图,△ABC的∠BAC=120 ,以BC为边向形外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60 后到△ECD的位置。若AB=3,AC=2,求∠BAD的度数和AD的长.
(
B
A
C
D
E
F
23题图
)23.如图所示,在边长为1的正方形ABCD中,E、F分别是AB、AD上的点,且AE+EF+FA=2,求∠ECF的度数.
24.如图,P是等边△ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB.
求:(1)PP′的长;(2)∠APB的度数.
25.如图,将△ABC绕点C逆时针旋转90°得△DEC,其中点A,点B的对应点分别是点D,点E,点B落在DE上,延长AC交DE于点F,AB、DC交于点G.
(1)求证:AB⊥DE;
(2)求证:FB+BG=BC.
第四章 图形的旋转与平移
一、选择题
1.A 2.B 3.B 4.B
5.B 6.A 7.C 8.B
9.A 10.C 11.C 12.B
二、填空题
13.2 14.4 15.点N 16.130
17.-7 18.
三、解答题
19 略
20. 解:(1)如图所示,△A'B'C'即为所求,A'的坐标为(0,4);
(2)若点M(m,n)是△ABC内部一点,则平移后对应点M'的坐标为(m+2,n+3),
故答案为:(m+2,n+3);
(3)△ABC的面积为×4×3=6;
(4)设P(0,m),
由题意:×4×|m+2|=×4×3,
解得m=1或﹣5,
∴P(0,1)或(0,﹣5).
21.解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求,B2(4,﹣1),C2(1,﹣2);
(3)如图,点P即为所求,点P的坐标(0,3).
22.∠BAD=60° AD=5
23. △EBC以C点为中心,顺时针旋转90°后,图形为△GDC
假设AE的长度是a,AF的长度是b
因为AE+EF+FA=2,正方形ABCD边长为1
所以EF=2-a-b
EB=GD=1-a
DF=1-b
GF=GD+DF=(1-a)+(1-b)=2-a-b
在△ECF和△CGF中
因为CF=CF
CE=CG
EF=GF=2-a-b
所以△ECF≌△CGF
所以∠ECF=∠GCF=∠DCG+∠DCF
又因为∠BCE=∠DCG
所以∠ECF=∠BCE+∠DCF
又因为∠BCD=90°
所以∠ECF=90÷2=45°
24. (1) (1)PP′=6
(2)∠APB=150°
25.证明:(1)∵将△ABC绕点C逆时针旋转90°得△DEC,
∴∠A=∠D,∠ACD=∠BCE=90°,
∵∠DGB=∠CGA,
∴∠DBG=∠ACG=90°,
∴AB⊥DE;
(2)∵将△ABC绕点C逆时针旋转90°得△DEC,
∴∠ABC=∠DEC,∠ACB=∠DCE,BC=EC,
∴∠ACB﹣90°=∠DCE﹣90°,即∠BCG=∠ECF,
∴△CBG≌△CEF(AAS),
∴EF=BG,
∴EF+BF=BG+BF,即BE=BG+BF,
∵EC=BC,∠BCE=90°,
∴△BCE为等腰直角三角形,
∴BE=BC,
即FB+BG=BC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
八年级数学上第四章《图形的旋转与平移》单元测试题
班级 姓名 成绩
一、选择题(每小题4分,共48分)
1. 下列标志既是轴对称图形又是中心对称图形的是( ).
A. B. C. D.
2.如图,把ABC经过一定的变换得到△A′B′C′,如果△ABC上点P的坐标为(x,y),那么这个点在△A′B′C′中的对应点P′的坐标为( )
(﹣x,y﹣2) B.(﹣x,y+2) C.(﹣x+2,﹣y) D.(﹣x+2,y+2)
3. 如图,平行四边形OABC的顶点O(0,0),B(2,2),若平行四边形绕点O逆时针旋转,每秒旋转45°,则第60秒时,顶点B的坐标为( )
A. (2,-2) B. (-2,-2) C. (2,0) D. (0,-2)
4.[2020·菏泽]如图,将△ABC绕点A顺时针旋转角α,得到△ADE,若点E恰好在CB的延长线上,则∠BED等于( )
A. B.α C.α D.180°-α
(
2
题图
)
3题图 4题图 6题图
5. 下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转改变图形的形状和大小
B.平移和旋转的共同点是改变图形的位置
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
6.如图,在中,,将绕点逆时针旋转,使点落在线段上的点处,点落在点处,则两点间的距离为( )
A. B. C. D.
7.如图,ΔABC和ΔADE均为正三角形,则图中可看作是旋转关系的三角形是( )
A.ΔABC和ΔADE B.ΔABC和ΔABD C.ΔABD和ΔACE D.ΔACE和ΔADE
(
D
) (
A
) (
9题图
) (
8题图
)
(
F
) (
E
) (
C
) (
B
) (
11题图
)
(
7题图
)
8.如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转900得到△DCF,连结EF,若∠BEC=600,则∠EFD的度数为( )
A.100 B.150 C.200 D.250
9.如图,两个边长相等的两个正方形ABCD和OEFG,若将正方形OEFG绕 点O按逆时针
方向旋转150°,两个正方形的重叠部分四边形OMCN的面积( )
A.不变 B.先增大再减小 C.先减小再增大 D.不断增大
10.钟表2时15分,时针与分针的夹角为( )
A.30° B.45° C.22.5° D.15°
11.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
12. 将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
二、填空题(每小题4分,共24分)
13. 如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
(
16题图
) (
14题图
)
13题图 15题图
14.已知两个重合的正方形纸片,边长为4厘米,其中ABCD沿AB方向平移3厘米,平移后的两个正方形重叠部分的面积是 平方厘米.
15.如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是___________
16.如图,在一块长方形ABCD草地上,AB=10,BC=15,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2个单位),空白部分表示的草地面积是 .
17.直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,
则x+2y= .
18.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=_________.
三、解答题(78分) 18题图
(
.
.
.
.
.
A
B
C
E
F
)19.经过平移,△ABC的边AB移到了EF作出平移后的三角形.
20.已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A'B'C'.
(1)请画出△A'B'C',写出A'的坐标;
(2)若点M(m,n)是△ABC内部一点,则平移后对应点M'的坐标为 ;
(3)求出△ABC的面积;
(4)点P在y轴上,且△BCP与△ABC的面积相等,求点P的坐标.
21.如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
(1)作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1(只画出图形).
(2)作出△ABC关于原点O成中对心称的△A2B2C2,(只画出图形),写出B2和C2的坐标.
(3)请在y轴上找一点P,使PB1+PC1的值最小,并直接写出点P的坐标.
20题图 21题图
22.如图,△ABC的∠BAC=120 ,以BC为边向形外作等边△BCD,把△ABD绕着D点按顺时针方向旋转60 后到△ECD的位置。若AB=3,AC=2,求∠BAD的度数和AD的长.
(
B
A
C
D
E
F
23题图
)23.如图所示,在边长为1的正方形ABCD中,E、F分别是AB、AD上的点,且AE+EF+FA=2,求∠ECF的度数.
24.如图,P是等边△ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB.
求:(1)PP′的长;(2)∠APB的度数.
25.如图,将△ABC绕点C逆时针旋转90°得△DEC,其中点A,点B的对应点分别是点D,点E,点B落在DE上,延长AC交DE于点F,AB、DC交于点G.
(1)求证:AB⊥DE;
(2)求证:FB+BG=BC.
第四章 图形的旋转与平移
一、选择题
1.A 2.B 3.B 4.B
5.B 6.A 7.C 8.B
9.A 10.C 11.C 12.B
二、填空题
13.2 14.4 15.点N 16.130
17.-7 18.
三、解答题
19 略
20. 解:(1)如图所示,△A'B'C'即为所求,A'的坐标为(0,4);
(2)若点M(m,n)是△ABC内部一点,则平移后对应点M'的坐标为(m+2,n+3),
故答案为:(m+2,n+3);
(3)△ABC的面积为×4×3=6;
(4)设P(0,m),
由题意:×4×|m+2|=×4×3,
解得m=1或﹣5,
∴P(0,1)或(0,﹣5).
21.解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求,B2(4,﹣1),C2(1,﹣2);
(3)如图,点P即为所求,点P的坐标(0,3).
22.∠BAD=60° AD=5
23. △EBC以C点为中心,顺时针旋转90°后,图形为△GDC
假设AE的长度是a,AF的长度是b
因为AE+EF+FA=2,正方形ABCD边长为1
所以EF=2-a-b
EB=GD=1-a
DF=1-b
GF=GD+DF=(1-a)+(1-b)=2-a-b
在△ECF和△CGF中
因为CF=CF
CE=CG
EF=GF=2-a-b
所以△ECF≌△CGF
所以∠ECF=∠GCF=∠DCG+∠DCF
又因为∠BCE=∠DCG
所以∠ECF=∠BCE+∠DCF
又因为∠BCD=90°
所以∠ECF=90÷2=45°
24. (1) (1)PP′=6
(2)∠APB=150°
25.证明:(1)∵将△ABC绕点C逆时针旋转90°得△DEC,
∴∠A=∠D,∠ACD=∠BCE=90°,
∵∠DGB=∠CGA,
∴∠DBG=∠ACG=90°,
∴AB⊥DE;
(2)∵将△ABC绕点C逆时针旋转90°得△DEC,
∴∠ABC=∠DEC,∠ACB=∠DCE,BC=EC,
∴∠ACB﹣90°=∠DCE﹣90°,即∠BCG=∠ECF,
∴△CBG≌△CEF(AAS),
∴EF=BG,
∴EF+BF=BG+BF,即BE=BG+BF,
∵EC=BC,∠BCE=90°,
∴△BCE为等腰直角三角形,
∴BE=BC,
即FB+BG=BC.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
