1.4 弹性碰撞与非弹性碰撞 (共17张PPT) 课件 2024-2025学年高二物理鲁科版(2019)选择性必修第一册
文档属性
| 名称 | 1.4 弹性碰撞与非弹性碰撞 (共17张PPT) 课件 2024-2025学年高二物理鲁科版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-09-20 16:28:55 | ||
图片预览






文档简介
(共17张PPT)
第一章 动量及其守恒定律
第4节 弹性碰撞与非弹性碰撞
碰撞的特点
(1)时间特点:碰撞现象中,相互作用的时间极短,相对物体运动的全过程可忽略不计。
(2)相互作用力特点:在碰撞过程中,系统的内力远大于外力,所以动量守恒。
那么,碰撞中的能量变化有什么特点呢?
学习目标
了解不同类型的碰撞,知道弹性碰撞、非弹性碰撞、完全非弹性碰撞的概念。
掌握弹性碰撞的规律,能用动量守恒定律和能量守恒处理弹性碰撞问题。
能根据弹性碰撞的规律解释判断有关的现象和解决有关的问题。
碰撞中有内能或其它形式能的产生,相互作用后,系统的动能减少。
物体碰撞后,形变能够完全恢复,不发热,不发声,没有动能损失。
1.弹性碰撞:
2.非弹性碰撞:
3.完全非弹性碰撞:
碰撞后结为一体,系统的动能损失最多。
知识点一:碰撞的分类(机械能是否损失)
例如钢球、玻璃球的碰撞,通常,分子、原子以及更小的粒子间的碰撞可视为弹性碰撞。
例如木制品的碰撞
例如橡皮泥球之间的碰撞
实验与探究
注意观察碰撞后两小球的状态和上升的高度
知识点二:弹性碰撞:
质量相等的两个钢球相碰
质量不相等的两个钢球相碰
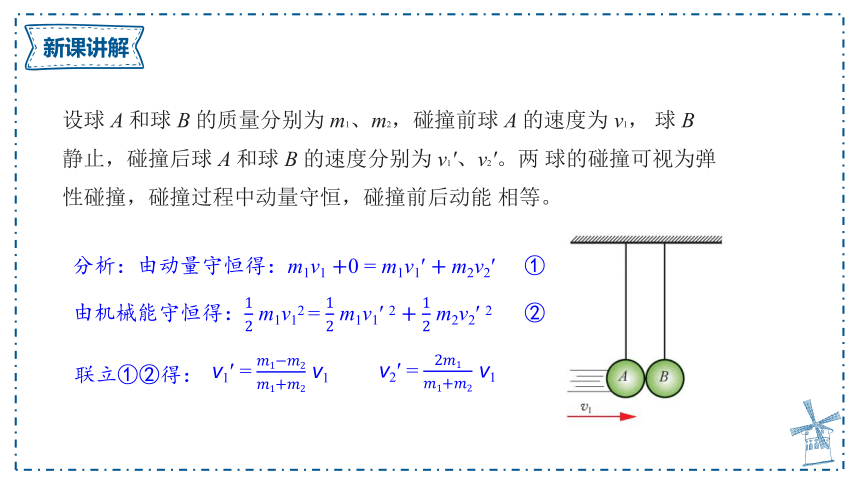
设球 A 和球 B 的质量分别为 m1、m2,碰撞前球 A 的速度为 v1, 球 B 静止,碰撞后球 A 和球 B 的速度分别为 v1′、v2′。两 球的碰撞可视为弹性碰撞,碰撞过程中动量守恒,碰撞前后动能 相等。
由机械能守恒得: m1v12 = m1v1′ 2 m2v2′ 2 ②
分析:由动量守恒得:m1v1 0 = m1v1′ m2v2′ ①
联立①②得:
v1′ = v1
v2′ = v1
①若m1=m2,得:v1′ = 0;v2′ = v1, 则:两小球交换速度.
v1′ = v1
v2′ = v1
②若,得:v1′> 0,v2′> 0,, 则:两球都向前运动。
③若,得:v1′< 0,v2′> 0, 则:碰撞后质量小的球被反弹回来。
设球 A 和球 B 的质量分别为 m1、m2,碰撞前球 A 的速度为 v1, 球 B 静止,碰撞后球 A 和球 B 的速度分别为 v1′、v2′
动量守恒:
机械能守恒:
请讨论:(1)当两球质量相等时,两球碰撞后的速度变化情况;
(2)当两球质量差异 较大且 v2 = 0 时,两球碰撞后的速度变化情况。
(1)
(2) v2 = 0 , 则
若,得:v1′ v1;v2′ 2v1, 则:m1速度几乎不变,
以近乎两倍的速度被撞出去.
若,得: 0, 则:m1几乎以原速弹回,
几乎不动.
例题:两个物体的质量都是m,碰撞以前一个物体静止,另一个以速度v向它撞去。碰撞以后两个物体粘在一起,成为一个质量为2m的物体,以速度v’继续前进。这个碰撞过程中能量守恒吗?
v
静止
m
m
v’
2m
根据动量守恒定律
碰撞后的共同速度
碰撞前的总动能
碰撞后的总动能
不守恒
知识点三:非弹性碰撞
如图1-33所示,打桩机重锤的质量为m1,从桩帽上方某高处由静止开始沿竖直方向自由落下,打在质量为m2的钢筋混凝土桩子上(包括桩帽)。锤与桩发生碰撞的时间极短,碰撞后二者以相同速度一起向下运动将桩打入地下。若碰撞前锤的速度为vo,求锤与桩所组成的系统碰撞后的动能及碰撞过程中损失的动能。
如图1-34所示,质量均为m 的物体B、C 静止在光滑水平面的同一直线上,一质量为m0的子弹A以速度v 射入物体B并嵌入其中。随后它们与C 发生弹性碰撞,求碰撞后B、C 的速度。
解答:选定子弹的初速度方向为正方向,设子弹嵌入B后,子弹与B的共同速度为,物体B、C碰撞后各自的速度为。子弹嵌入物体B的过程,根据动量守恒定律有
物体B、C碰撞的过程根据动量守恒定律和动能不变有
由以上各式解得
1.质量为 1 kg 的物体 A 在光滑水平面上以 6 m/s 的速度与质量为 2 kg、速度为 2 m/s 的物体 B 发 生正碰。碰撞后 A、B 两物体的速度可能值为 ( )
A. vA = 5 m/s,vB = 2.5 m/s
B. vA = 2 m/s,vB = 4 m/s
C. vA = -4 m/s,vB = 7 m/s
D. vA = 7 m/s,vB = 1.5 m/s
B
2.如图,材料的种类未定,但是质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6m/s,B球的速度是-2m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的哪一种猜测结果一定无法实现( )
A.vA′=-2 m/s,vB′ =6 m/s
B.vA′ =2 m/s,vB′ =2 m/s
C.vA′ =1 m/s, vB′ =3 m/s
D.vA′ =-3 m/s,vB′ =7 m/s
D
弹性碰撞和非弹性碰撞
弹性碰撞
非弹性碰撞
完全非弹性碰撞
第一章 动量及其守恒定律
第4节 弹性碰撞与非弹性碰撞
碰撞的特点
(1)时间特点:碰撞现象中,相互作用的时间极短,相对物体运动的全过程可忽略不计。
(2)相互作用力特点:在碰撞过程中,系统的内力远大于外力,所以动量守恒。
那么,碰撞中的能量变化有什么特点呢?
学习目标
了解不同类型的碰撞,知道弹性碰撞、非弹性碰撞、完全非弹性碰撞的概念。
掌握弹性碰撞的规律,能用动量守恒定律和能量守恒处理弹性碰撞问题。
能根据弹性碰撞的规律解释判断有关的现象和解决有关的问题。
碰撞中有内能或其它形式能的产生,相互作用后,系统的动能减少。
物体碰撞后,形变能够完全恢复,不发热,不发声,没有动能损失。
1.弹性碰撞:
2.非弹性碰撞:
3.完全非弹性碰撞:
碰撞后结为一体,系统的动能损失最多。
知识点一:碰撞的分类(机械能是否损失)
例如钢球、玻璃球的碰撞,通常,分子、原子以及更小的粒子间的碰撞可视为弹性碰撞。
例如木制品的碰撞
例如橡皮泥球之间的碰撞
实验与探究
注意观察碰撞后两小球的状态和上升的高度
知识点二:弹性碰撞:
质量相等的两个钢球相碰
质量不相等的两个钢球相碰
设球 A 和球 B 的质量分别为 m1、m2,碰撞前球 A 的速度为 v1, 球 B 静止,碰撞后球 A 和球 B 的速度分别为 v1′、v2′。两 球的碰撞可视为弹性碰撞,碰撞过程中动量守恒,碰撞前后动能 相等。
由机械能守恒得: m1v12 = m1v1′ 2 m2v2′ 2 ②
分析:由动量守恒得:m1v1 0 = m1v1′ m2v2′ ①
联立①②得:
v1′ = v1
v2′ = v1
①若m1=m2,得:v1′ = 0;v2′ = v1, 则:两小球交换速度.
v1′ = v1
v2′ = v1
②若,得:v1′> 0,v2′> 0,, 则:两球都向前运动。
③若,得:v1′< 0,v2′> 0, 则:碰撞后质量小的球被反弹回来。
设球 A 和球 B 的质量分别为 m1、m2,碰撞前球 A 的速度为 v1, 球 B 静止,碰撞后球 A 和球 B 的速度分别为 v1′、v2′
动量守恒:
机械能守恒:
请讨论:(1)当两球质量相等时,两球碰撞后的速度变化情况;
(2)当两球质量差异 较大且 v2 = 0 时,两球碰撞后的速度变化情况。
(1)
(2) v2 = 0 , 则
若,得:v1′ v1;v2′ 2v1, 则:m1速度几乎不变,
以近乎两倍的速度被撞出去.
若,得: 0, 则:m1几乎以原速弹回,
几乎不动.
例题:两个物体的质量都是m,碰撞以前一个物体静止,另一个以速度v向它撞去。碰撞以后两个物体粘在一起,成为一个质量为2m的物体,以速度v’继续前进。这个碰撞过程中能量守恒吗?
v
静止
m
m
v’
2m
根据动量守恒定律
碰撞后的共同速度
碰撞前的总动能
碰撞后的总动能
不守恒
知识点三:非弹性碰撞
如图1-33所示,打桩机重锤的质量为m1,从桩帽上方某高处由静止开始沿竖直方向自由落下,打在质量为m2的钢筋混凝土桩子上(包括桩帽)。锤与桩发生碰撞的时间极短,碰撞后二者以相同速度一起向下运动将桩打入地下。若碰撞前锤的速度为vo,求锤与桩所组成的系统碰撞后的动能及碰撞过程中损失的动能。
如图1-34所示,质量均为m 的物体B、C 静止在光滑水平面的同一直线上,一质量为m0的子弹A以速度v 射入物体B并嵌入其中。随后它们与C 发生弹性碰撞,求碰撞后B、C 的速度。
解答:选定子弹的初速度方向为正方向,设子弹嵌入B后,子弹与B的共同速度为,物体B、C碰撞后各自的速度为。子弹嵌入物体B的过程,根据动量守恒定律有
物体B、C碰撞的过程根据动量守恒定律和动能不变有
由以上各式解得
1.质量为 1 kg 的物体 A 在光滑水平面上以 6 m/s 的速度与质量为 2 kg、速度为 2 m/s 的物体 B 发 生正碰。碰撞后 A、B 两物体的速度可能值为 ( )
A. vA = 5 m/s,vB = 2.5 m/s
B. vA = 2 m/s,vB = 4 m/s
C. vA = -4 m/s,vB = 7 m/s
D. vA = 7 m/s,vB = 1.5 m/s
B
2.如图,材料的种类未定,但是质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6m/s,B球的速度是-2m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的哪一种猜测结果一定无法实现( )
A.vA′=-2 m/s,vB′ =6 m/s
B.vA′ =2 m/s,vB′ =2 m/s
C.vA′ =1 m/s, vB′ =3 m/s
D.vA′ =-3 m/s,vB′ =7 m/s
D
弹性碰撞和非弹性碰撞
弹性碰撞
非弹性碰撞
完全非弹性碰撞
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
