(核心素养应用意识)第八单元数学广角-数与形(解决问题含答案)六年级数学上册人教版.docx
文档属性
| 名称 | (核心素养应用意识)第八单元数学广角-数与形(解决问题含答案)六年级数学上册人教版.docx |  | |
| 格式 | docx | ||
| 文件大小 | 910.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-19 20:14:09 | ||
图片预览



文档简介
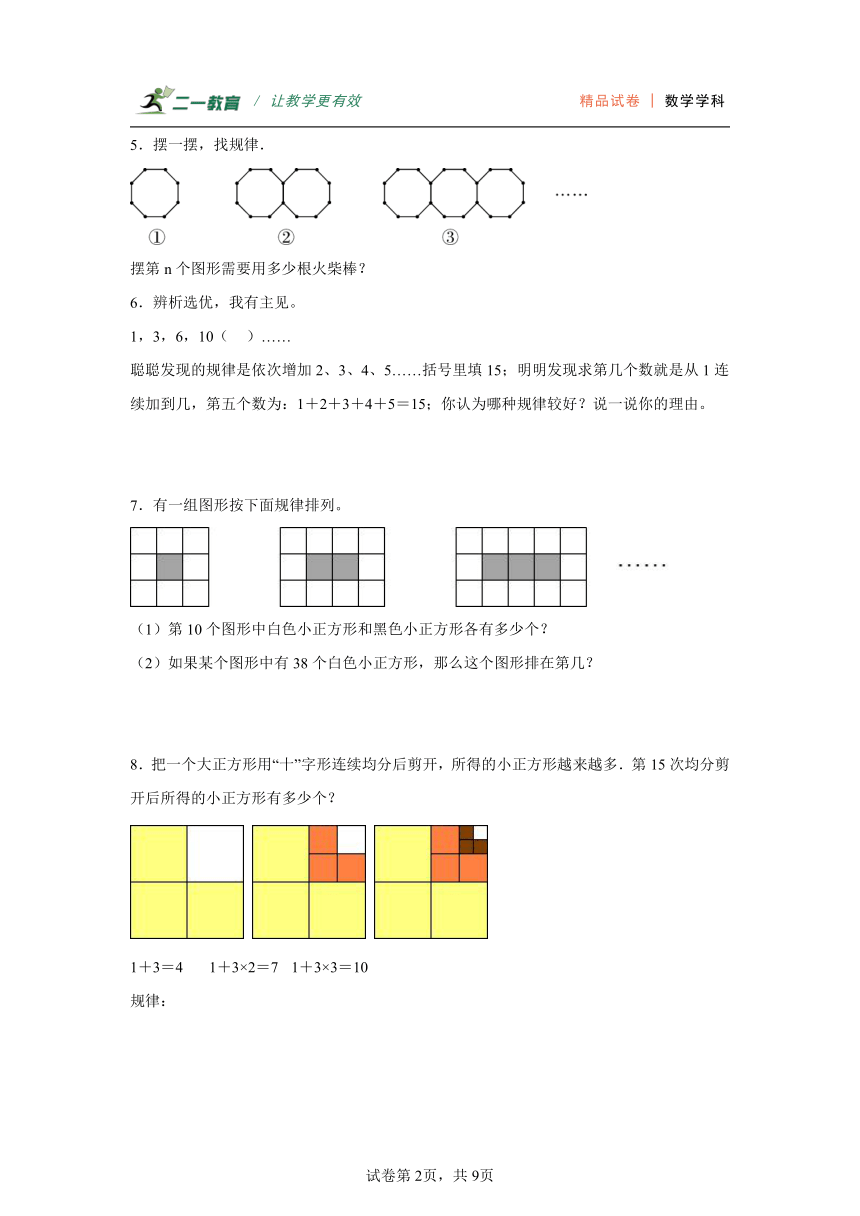
第八单元数学广角-数与形(解决问题)六年级数学上册人教版
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.有个选手进行乒乓球单循环赛,结果每人获胜局数各不相同,那么冠军胜了几局?
2.按如图的方式摆桌子和椅子,一张桌子可坐4人,两张桌子可坐6人……照这样摆下去。
(1)10张桌子可坐多少人?
(2)n张桌子可坐多少人?
(3)坐80人需要多少张桌子?
3.在图中的A、B、C三个圆圈内填入三个不同的自然数,使得三角形每条边上的三个数之和都等于10,那么圆圈B中应填的数是多少?
4.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.请写出第5个图形的算式.
4=1+3 9=3+6 16=6+10
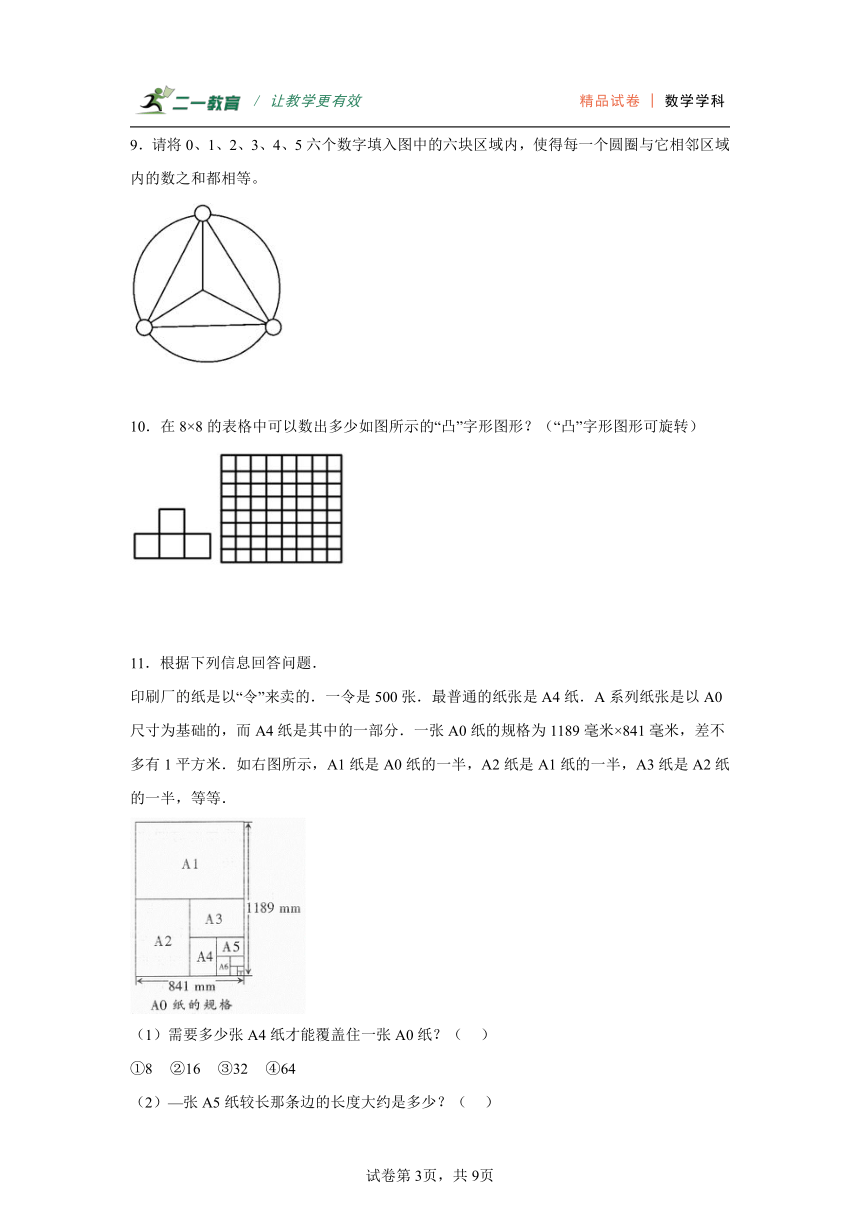
5.摆一摆,找规律.
摆第n个图形需要用多少根火柴棒?
6.辨析选优,我有主见。
1,3,6,10( )……
聪聪发现的规律是依次增加2、3、4、5……括号里填15;明明发现求第几个数就是从1连续加到几,第五个数为:1+2+3+4+5=15;你认为哪种规律较好?说一说你的理由。
7.有一组图形按下面规律排列。
(1)第10个图形中白色小正方形和黑色小正方形各有多少个?
(2)如果某个图形中有38个白色小正方形,那么这个图形排在第几?
8.把一个大正方形用“十”字形连续均分后剪开,所得的小正方形越来越多.第15次均分剪开后所得的小正方形有多少个?
1+3=4 1+3×2=7 1+3×3=10
规律:
9.请将0、1、2、3、4、5六个数字填入图中的六块区域内,使得每一个圆圈与它相邻区域内的数之和都相等。
10.在8×8的表格中可以数出多少如图所示的“凸”字形图形?(“凸”字形图形可旋转)
11.根据下列信息回答问题.
印刷厂的纸是以“令”来卖的.一令是500张.最普通的纸张是A4纸.A系列纸张是以A0尺寸为基础的,而A4纸是其中的一部分.一张A0纸的规格为1189毫米×841毫米,差不多有1平方米.如右图所示,A1纸是A0纸的一半,A2纸是A1纸的一半,A3纸是A2纸的一半,等等.
(1)需要多少张A4纸才能覆盖住一张A0纸?( )
①8 ②16 ③32 ④64
(2)—张A5纸较长那条边的长度大约是多少?( )
①420mm ②297mm ③210mm ④149mm
12.先画出第五个图形,再填空:第10个方框里有 个点,第n个方框里有 个点。
13.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
14.如图,堆三角形积木。
①如果下层放6个,一共需要多少个三角形?
②如果有169个三角形积木块,下层应放几个?
15.第4和第5幅图的个数是多少?你从中发现了什么数学规律?
16.观察点阵与算式的对应规律,并填空.
…… ……
①1 ②1+4 ③1+4+4 ④1+4+4+4 ⑤…… ⑥
第⑥个点阵图中有多少个点
17.龙一鸣、黄霏霏、苹苹、淘淘和依依5个好朋友聚会,每两人之间都要握一次手.已知龙一鸣已经握了4次手,黄霏霏已经握了3次手,依依已经握了2次手,苹苹已经握了1次手.淘淘一共握了几次手?分别与谁握的?(可画图连一连)
18.如图中数字排列:问:第20行第7个是多少?
19.用所学知识解决下列问题.
+++++……=
20.仔细观察下面的数列,说说你发现它有什么特点和规律,并按照数列的规律,写出2011个分数。
…
21.用花、白两种正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用花瓷砖(如图所示)。
(1)填写下列表格。
大正方形每边的瓷砖块数 3 4 5 6 7 …
花瓷砖块数 8 …
(2)如果所拼的图形中,用了20块花瓷砖,那么白瓷砖用了多少块?
(3)如果所拼的图形中,用了n2块白瓷砖,那么花瓷砖用了多少块?
22.一张桌子摆4把椅子,两张桌子并起来摆6把椅子……照这样摆下去。
(1)6张桌子可以摆多少把椅子?
(2)n张桌子可以摆多少把椅子?用式子表示出来是( )把。
(3)如果有34人,需要并起来多少张桌子才能坐下?
在10×19方格表的每个方格内,写上0或1,然后算出每行及每列的各数之和。问最多能得到多少个不同的和数?
24.观察下图,按要求完成下列各题。
(1)这4个图形中分别有多少个三角形?请依次写出。
(2)按照这种规律画下去,第6个图形中有多少个三角形呢?第9个图形中有多少个三角形呢?
(3)仔细观察图形,你能发现什么规律?请推测第n个图形中有多少个三角形。
(4)根据上面的规律,请计算下图中一共有多少个三角形。
小明用小棒搭房子,搭2间用9根,搭3间用13根,照这样计算,如果搭10间房子,需要用多少根小棒?
26.下图中摆一个三角形需要用3根火柴棒,摆2个,3个,4个,5个,6个呢?
三角形的个数/个 1 2 3 4 5 6 ……
火柴棒的根数/根 3 ……
如果继续摆下去,你有什么发现?
丁丁觉得游戏很有意思,对牛牛说:“我这儿也有个游戏,有一列数1,3,5,7,9,1,3,5,7,9,1,3,5,7,9,…,问前48个数之和是多少?”
28.下图是百世超市一月份统计的营业额中各种支付方式情况统计图.
(1)财付通支付占百分之几?哪种支付方式所占百分比最多?
(2)你还了解到了哪些信息?
(3)看到上面的统计图,你想到了什么?
一个杯子口朝上,翻动一次杯口朝下,翻动两次杯口朝上,那么翻动56次杯口朝哪里?并说明理由.
30.如下图,1张桌子可以坐4人,2张桌子拼起来可以坐6人,3张桌子拼起来可以坐8人.
(1)像这样的4张桌子拼起来可以坐多少人?
(2)像这样的6张桌子拼起来可以坐多少人?
(3)如果有40人,那么需要多少张这样的桌子拼起来?
31.一条线段把一个长方形分为两部分,4条线段最多能把一个长方形分成几部分?20条呢?
32.一种细胞在培养过程中,每30分钟要分裂一次(1个母细胞一分为二成2个子细胞)。这种细胞如果要由1个分裂成8个,需要多少分钟?(请用画图的方法解释说明)
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.局
【分析】8个选手进行乒乓球单循环赛,每个选手都要参加7场比赛,而且每人获胜局数各不相同,所以每人获胜的局数分别为0~7局,那么冠军胜了7局。
【详解】单循环赛,每个人都要和其余的每个人进行比赛;
8-1=7(场)
每个选手都要参加7场比赛,既然每人获胜局数各不相同,那么只能是0~7;
冠军的胜场数肯定是最大的,所以冠军胜了7局;
答:冠军胜了7局。
【点睛】本题考查的是体育比赛中的数学问题,单循环比赛,n个队伍,每个队伍要比n-1场。
2.(1)22人
(2)(2n+2)人
(3)39张
【分析】一张桌子可以坐4人,后面每增加一张桌子,增加2个人,即1张桌坐4人;2张桌子坐4+2×(2-1)=6(人);3张桌子坐4+2×(3-1)=8(人);……(1)10张桌子可坐4+2×(10-1)=22(人);(2)n张桌子可坐4+2×(n-1)=2n+2(人);(3)设坐80人需要x张桌子,求解x即可。
【详解】(1)4+2×(10-1)
=4+18
=22(人);
答:10张桌子可坐22人。
(2)4+2×(n-1)=2n+2(人);
答:n张桌子可坐2n+2人。
(3)设需要x张桌子
2x+2=80
2x=78
x=39
答:坐80人需要39张桌子。
【点睛】考查数与形的找规律问题的实际应用,解方程的应用。按照将形化为数字,拆解研究规律即可。
3.1
【分析】封闭型数阵图,线和是10,先求A,再求B,再求C。
【详解】A=
B=
【点睛】本题较为简单,根据数阵图的基本要求直接求解即可。
4.36=15+21
【详解】题目中“三角形数”的规律为1、3、6、10、15、21…“正方形数”的规律为1、4、9、16、25…,根据题目已知条件:从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.可得出最后结果 .
5.(7n+1)根
【详解】略
6.我认为明明发现的规律较好,对于较大的数更好计算。
【分析】聪聪和明明发现的规律都很正确,但是聪聪的计算相较而言麻烦一点,随着要求数位的增加,明明的计算更加简单一点。
【详解】1=1=
1+2=3=
1+2+3=6=
故1+2+3+…+n=
所以对于较大的数,相比明明发现的规律更好计算。
答:我认为明明发现的规律较好,对于较大的数更好计算。
【点睛】本题主要考查找规律。
7.(1)白:26个;黑:10个
(2)16
【分析】(1)第1个图形一共有(3×3)个小正方形,有1个黑色小正方形,有(3×3-1)个白色小正方形;
第2个图形一共有(3×4)个小正方形,有2个黑色小正方形,有(3×4-2)个白色小正方形;
第3个图形一共有(3×5)个小正方形,有3个黑色小正方形,有(3×3-3)个白色小正方形;
……
第n个图形一共有3(n+2)=(3n+6)个小正方形,有n个黑色小正方形,有3n+6-n=2n+6个白色小正方形;
(2)把白色小正方形的个数代入表示白色小正方形含有字母的式子,求出n的值即可。
【详解】(1)分析图形规律可知:
第n个图形小正方形的总个数:3(n+2)=3n+6
第n个图形黑色小正方形的个数:n个
第n个图形白色小正方形的个数:3n+6-n=2n+6
当n=10时,
白色小正方形的个数:2n+6=2×10+6=26(个)
黑色小正方形的个数:10个
答:第10个图形中白色小正方形有26个,黑色小正方形有10个。
(2)由题意可知,
2n+6=38
解:2n=38-6
2n=32
n=32÷2
n=16
答:如果某个图形中有38个白色小正方形,那么这个图形排在第16。
【点睛】分析图形找出图形变化的规律,并用含有字母的式子表示出规律是解答题目的关键。
8.46个
每均分一次,正方形的个数增加3个;均分n次,正方形的个数就增加3n个.
【详解】1+3×15=46(个)
9.
【分析】复合型数阵图问题,每块区域的数都重复了一次,利用数和、线和的关系进行求解。
【详解】如图,令;
已知a,b,c,d,e,f各自用了两次,计算数和,;
令,解得;
容易得出0+1+4+5=10,0+2+3+5=10,1+2+3+4=10,如图,合理构造,得出最后的填法。
【点睛】复合型数阵图较为复杂,需要将辐射型、闭合型数阵图的方法综合起来求解,最关键的还是判断每一块的重复次数。
10.168个
【分析】如图,在每一个2×3的长方形里面,都可以找到两个目标图形,所以数出2×3的长方形个数,乘2得到目标图形的个数。
【详解】如图所示:
每2行可以数出6个2×3的长方形,每两列也可以数出6个2×3的长方形;
(个)
(个)
答:可以数出168个如图所示的“凸”字形图形。
【点睛】本题考查的是图形计数问题,可以将数目标图形转化成比较容易数的长方形。
11.(1)② (2)③
12.见详解;37;1+4(n-1)
【分析】第1个图形,1个点;
第2个图形,5个点,5=1+4=1+4×(2-1);
第3个图形,9个点,9=1+4×2=1+4×(3-1);
第4个图形,13个点,13=1+4×3=1+4×(4-1);
……
第n个图形的点数是1+4(n-1)个;
据此规律解答。
【详解】第五个图形有(1+4×4)个点。
如图:
第n个方框里有1+4(n-1)个点。
当n=10时
1+4(n-1)
=1+4×(10-1)
=1+4×9
=1+36
=37(个)
第10个方框里有37个点,第n个方框里有1+4(n-1)个点。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
13.(1)16张;(2)(10+2n)厘米.
【详解】(1)由图可知:第(1)个图形的小正方形卡纸个数为3×3-1,第(2)个图形的个数为3×4-2,第(3)个图形的个数为3×5-3,像这样拼下去,第(5)个图形用3×7-5=16张小正方形卡纸.
(2)第n个图形周长=(3+2+n)×2=10+2n(厘米)
14.①36个
②13个
【分析】①根据题图可知,第一个图形下层放2个,有4个三角形,第二个图形下层放3个,有9个三角形,第三个图形下层放4个,有16个三角形,据此可知,三角形的个数是下层放的个数的平方,当下层放6个时,则有6×6=36个小三角形;
②因为13×13=169,所以如果有169个三角形积木块,下层应放了13个,据此解答即可。
【详解】①6×6=36个;
答:如果下层放6个,一共需要36个三角形。
②13×13=169;
答:如果有169个三角形积木块,下层应放了13个。
【点睛】根据已知图形找到底层个数与三角形总个数的关系是解答本题的关键。
15.第四幅图有16个,第五幅有25个.
根据图意,第一幅点子的个数是12个.第二幅图是22个点子排成的正方形,第三幅图是32个点子,因此第四幅图是42个点子排成的正方形,第五幅图是52个点子排成的正方形,如图.
第四幅图是 ,第五幅图
【详解】略
16.根据题干中的已知图形中点数特点,可以探索出这组图形的一般规律,并利用规律进行解答.
观察图形可得:第一个图形有1个点,可以写作1+(1-1)×4;
第二个图形有1+4(个)点,可以写作1+(2-1)×4;
第三个图形有1+4+4(个)点,可以写作1+(3-1)×4……
则第n个图形的点数就可以写作1+(n-1)×4.
当n=6时,点数为1+(6-1)×4=21(个)
【详解】略
17.
由图可以看出淘淘一共握了两次手,分别是与龙一鸣和黄霏霏握的.
【解析】略
18.368
【分析】由图中可知:每行的末尾是行数的平方,下一行数的第一个数等于上一行末尾的数加1。
第一行的末尾是1的平方,第二行的末尾是2的平方是4;第三行的末尾是3的平方是9;第四行的末尾是4的平方是16;以此类推,第19行的末尾是19的平方是361,第20行末尾的数是20的平方是400;据此解答。
【详解】由分析可得:第19行的末尾是19的平方是361。
所以第20行的第一个数是361+1=362
那么,第7个数是362+(7-1)=368
答:第20行第7个是368。
【点睛】本题考查了数字排列的关系,此题的关键是要理解每行的末尾是行数的平方,下一行数的第一个数等于上一行末尾的数加1。
19.1
【详解】
从图上可以看出这些分数不断加下去,总和就是一
20.
【分析】把1换成,利用分数的基本性质,分子分母同时乘一个数,值不变,把化成,化成,化成,即可看出规律,对应第n项,分子等于n+1,分母等于2n因此得解。
【详解】将原数列变为…由此得出分子为n+1,分母为2n(n为第几个数),所以第2011个分数为,化简得。
【点睛】主要考查探索规律的实际能力,关键是先找出规律,然后根据规律写出第2011个分数,根据这个可以直接解答,注意解答的准确性。
21.(1)12;16;20;24 (2) 16块 (3) (4n+4)块
【详解】(2)(20÷4-1)×(20÷4-1)=16(块)
答:白瓷砖用了16块。
(3)n2=n×n,(n+1)×4=4n+4(块)。
答:花瓷砖用了(4n+4)块。
22.(1)14把;
(2)2n+2;
(3)16张
【分析】由图可知,1张桌子时,可以摆4把椅子;2张桌子时,可以摆(4+2)把椅子;3张桌子时,可以摆(4+2+2)把椅子……每增加一张桌子就增加2把椅子,那么n张桌子时,可以摆4+2(n-1)把椅子;最后计算出椅子数量为34时,n的值即可。
【详解】(1)1张桌子可以摆椅子的数量:4把
2张桌子可以摆椅子的数量:4+2=6(把)
3张桌子可以摆椅子的数量:4+2×2=4+4=8(把)
4张桌子可以摆椅子的数量:4+3×2=4+6=10(把)
5张桌子可以摆椅子的数量:4+4×2=4+8=12(把)
6张桌子可以摆椅子的数量:4+5×2=4+10=14(把)
答:6张桌子可以摆14把椅子。
(2)分析可知,n张桌子可以摆椅子的数量:4+2(n-1)=4+2n-2=(2n+2)把
(3)如果有34人,那么需要34把椅子。
2n+2=34
解:2n=34-2
2n=32
n=32÷2
n=16
答:如果有34人,需要并起来16张桌子才能坐下。
【点睛】分析题意找出椅子数量变化的规律是解答题目的关键。
23.19个
【分析】每列的和最少为0,最多是10,每行的和最少是0,最多是19,所以不同的和最多也就是0,1,2,3,4,…,18,19这20个。
【详解】首先每列的和最少为0,最多是10,每行的和最少是0,最多是19,所以不同的和最多也就是0,1,2,3,4,…,18,19这20个。如果和是0出现,那么必然有另外一个数字不能出现。如果0出现在行的和中,说明有1行全是0,意味着列的和中至多出现0到9,加上行的和至多出现10个数字,所以少了一种可能。如果0出现在列的和中,说明在行的和中19不可能出现,所以0出现就意味着另一个数字不能出现,所以至多是19。如下图所示:
除去重复的和,所以和最多是19个。
答: 最多能得到19个不同的和数。
【点睛】我们先弄清楚题意,分行分列的分别求出和,最后算出不同和的个数,综合考虑此题中最小和是0,最大和是19。假设每一行全写0则和是0,写上1个1则和是1,以此类推可得出最多的和的个数是19个。
24.(1)1个;3个;6个;10个;
(2)21个;45个;
(3)见详解;(1+2+3+4+…+n)个;
(4)55个
【分析】从图中可知:
(1)有1个三角形;
有2个小三角形和1个大三角形,一共是2+1=3(个)三角形;
有3个小三角形,相邻2个小三角形组成2个三角形,有1个大三角形,共有3+2+1=6(个)三角形;
有4个小三角形,相邻2个小三角形组成3个三角形,相邻3个小三角形组成2个三角形,有1个大三角形,共有4+3+2+1=10(个)三角形;
(2)按照这种规律画下去,
第6个图形:6+5+4+3+2+1=21(个)
第9个图形:9+8+7+6+5+4+3+2+1=45(个)
(3)由此得出规律:若图形中的单个小三角形个数为n,则图形中三角形的总个数就是(1+2+3+4+…+n)个。
(4)数出单个小三角形的个数,再按规律计算即可。
【详解】(1)1个
2+1=3(个)
3+2+1=6(个)
4+3+2+1=10(个)
答:第1个图形有1个三角形;第2个图形有3个三角形;第3个图形有6个三角形;第4个图形有10个三角形。
(2)第6个图形:6+5+4+3+2+1=21(个)
第9个图形:9+8+7+6+5+4+3+2+1=45(个)
答:第6个图形有21个三角形;第9个图形有45个三角形;
(3)答:我发现图中有几个小三角形就从1开始依次加到n。若图形中的单个小三角形个数为n,则图形中三角形的总个数就是(1+2+3+4+…+n)个。
(4)10+9+8+7+6+5+4+3+2+1=55(个)
答:图中一共有55个三角形。
25.41根
【详解】根据图示,
2间房:5+4=9(根)
3间房:5+4+4=13(根)
……
10间房:5+4×(10﹣1)=41(根)
答:搭10间房子,需要用41根小棒。
26.5;7;9;11;13
发现:火柴棒的根数=三角形的个数×2+1
【详解】略
27.234
【分析】观察数列可知,数列是按照1,3,5,7,9 循环进行排列的,先求出一组的和是多少,然后再求出前48个数共有多少组,余数是几就从左向右数几,然后相加即可。
【详解】1+3+5+7+9
=4+5+7+9
=9+7+9
=16+9
=25
48÷5=9(组) 3(个)
25×9+1+3+5
=225+1+3+5
=226+3+5
=229+5
=234
答:前48个数之和是234。
【点睛】本题考查循环数列,明确共有几个循环是解题的关键。
28.(1)1-40%-16%-20%-18%=6% 支付宝
(2)使用财付通支付的最少等.(答案不唯一)
(3)现在购物的支付方式越来越多,用现金支付的人逐渐减少.(答案不唯一,合理即可)
【解析】略
29.朝上,翻动偶数次与原来状态相同,翻动奇数次与原来状态相反
【详解】由题意可知:杯子翻动杯子1次,杯口朝下,翻动2次杯口朝上,翻动3次,杯口朝下,翻动4次,杯口朝上…,得出:翻动偶数次与原来状态相同,翻动奇数次与原来状态相反;
因为56是偶数;
所以翻动56次,杯口朝上.
答:翻动56次,杯口朝上.
30.(1)4×2+2=10(人)
(2)6×2+2=14(人)
(3)(40-2)÷2=19(张)
【解析】略
31.11部分,211部分
【分析】1条线段以后的规律:分成的部分=2+2+3+……+线段条数,由此根据规律计算即可.
【详解】
1条线段把长方形分为2部分.2
2条线段把长方形分为4部分,使分得的部分在原来的基础上增加了2部分.
3条线段把长方形分为7部分,使分得的部分在原来的基础上增加了3部分.
4条线段把长方形分成2+2+3+4=11部分.
20条线段就把长方形分成2+2+3+…+20=211部分.
答:4条最多能把一个长方形分成11部分,20条最对能分成211部分.
32.90分钟
【分析】一个细胞经过30分钟分裂成2个细胞,2个细胞经过30分钟分裂成4个细胞,4个细胞经过30分钟分裂成8个细胞,据此解答。
【详解】画图如下。
30×3=90(分钟)
答:需要90分钟。
【点睛】解决此题的关键是确定一个母细胞分裂成8个子细胞需要分裂的次数。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.有个选手进行乒乓球单循环赛,结果每人获胜局数各不相同,那么冠军胜了几局?
2.按如图的方式摆桌子和椅子,一张桌子可坐4人,两张桌子可坐6人……照这样摆下去。
(1)10张桌子可坐多少人?
(2)n张桌子可坐多少人?
(3)坐80人需要多少张桌子?
3.在图中的A、B、C三个圆圈内填入三个不同的自然数,使得三角形每条边上的三个数之和都等于10,那么圆圈B中应填的数是多少?
4.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.请写出第5个图形的算式.
4=1+3 9=3+6 16=6+10
5.摆一摆,找规律.
摆第n个图形需要用多少根火柴棒?
6.辨析选优,我有主见。
1,3,6,10( )……
聪聪发现的规律是依次增加2、3、4、5……括号里填15;明明发现求第几个数就是从1连续加到几,第五个数为:1+2+3+4+5=15;你认为哪种规律较好?说一说你的理由。
7.有一组图形按下面规律排列。
(1)第10个图形中白色小正方形和黑色小正方形各有多少个?
(2)如果某个图形中有38个白色小正方形,那么这个图形排在第几?
8.把一个大正方形用“十”字形连续均分后剪开,所得的小正方形越来越多.第15次均分剪开后所得的小正方形有多少个?
1+3=4 1+3×2=7 1+3×3=10
规律:
9.请将0、1、2、3、4、5六个数字填入图中的六块区域内,使得每一个圆圈与它相邻区域内的数之和都相等。
10.在8×8的表格中可以数出多少如图所示的“凸”字形图形?(“凸”字形图形可旋转)
11.根据下列信息回答问题.
印刷厂的纸是以“令”来卖的.一令是500张.最普通的纸张是A4纸.A系列纸张是以A0尺寸为基础的,而A4纸是其中的一部分.一张A0纸的规格为1189毫米×841毫米,差不多有1平方米.如右图所示,A1纸是A0纸的一半,A2纸是A1纸的一半,A3纸是A2纸的一半,等等.
(1)需要多少张A4纸才能覆盖住一张A0纸?( )
①8 ②16 ③32 ④64
(2)—张A5纸较长那条边的长度大约是多少?( )
①420mm ②297mm ③210mm ④149mm
12.先画出第五个图形,再填空:第10个方框里有 个点,第n个方框里有 个点。
13.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
14.如图,堆三角形积木。
①如果下层放6个,一共需要多少个三角形?
②如果有169个三角形积木块,下层应放几个?
15.第4和第5幅图的个数是多少?你从中发现了什么数学规律?
16.观察点阵与算式的对应规律,并填空.
…… ……
①1 ②1+4 ③1+4+4 ④1+4+4+4 ⑤…… ⑥
第⑥个点阵图中有多少个点
17.龙一鸣、黄霏霏、苹苹、淘淘和依依5个好朋友聚会,每两人之间都要握一次手.已知龙一鸣已经握了4次手,黄霏霏已经握了3次手,依依已经握了2次手,苹苹已经握了1次手.淘淘一共握了几次手?分别与谁握的?(可画图连一连)
18.如图中数字排列:问:第20行第7个是多少?
19.用所学知识解决下列问题.
+++++……=
20.仔细观察下面的数列,说说你发现它有什么特点和规律,并按照数列的规律,写出2011个分数。
…
21.用花、白两种正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用花瓷砖(如图所示)。
(1)填写下列表格。
大正方形每边的瓷砖块数 3 4 5 6 7 …
花瓷砖块数 8 …
(2)如果所拼的图形中,用了20块花瓷砖,那么白瓷砖用了多少块?
(3)如果所拼的图形中,用了n2块白瓷砖,那么花瓷砖用了多少块?
22.一张桌子摆4把椅子,两张桌子并起来摆6把椅子……照这样摆下去。
(1)6张桌子可以摆多少把椅子?
(2)n张桌子可以摆多少把椅子?用式子表示出来是( )把。
(3)如果有34人,需要并起来多少张桌子才能坐下?
在10×19方格表的每个方格内,写上0或1,然后算出每行及每列的各数之和。问最多能得到多少个不同的和数?
24.观察下图,按要求完成下列各题。
(1)这4个图形中分别有多少个三角形?请依次写出。
(2)按照这种规律画下去,第6个图形中有多少个三角形呢?第9个图形中有多少个三角形呢?
(3)仔细观察图形,你能发现什么规律?请推测第n个图形中有多少个三角形。
(4)根据上面的规律,请计算下图中一共有多少个三角形。
小明用小棒搭房子,搭2间用9根,搭3间用13根,照这样计算,如果搭10间房子,需要用多少根小棒?
26.下图中摆一个三角形需要用3根火柴棒,摆2个,3个,4个,5个,6个呢?
三角形的个数/个 1 2 3 4 5 6 ……
火柴棒的根数/根 3 ……
如果继续摆下去,你有什么发现?
丁丁觉得游戏很有意思,对牛牛说:“我这儿也有个游戏,有一列数1,3,5,7,9,1,3,5,7,9,1,3,5,7,9,…,问前48个数之和是多少?”
28.下图是百世超市一月份统计的营业额中各种支付方式情况统计图.
(1)财付通支付占百分之几?哪种支付方式所占百分比最多?
(2)你还了解到了哪些信息?
(3)看到上面的统计图,你想到了什么?
一个杯子口朝上,翻动一次杯口朝下,翻动两次杯口朝上,那么翻动56次杯口朝哪里?并说明理由.
30.如下图,1张桌子可以坐4人,2张桌子拼起来可以坐6人,3张桌子拼起来可以坐8人.
(1)像这样的4张桌子拼起来可以坐多少人?
(2)像这样的6张桌子拼起来可以坐多少人?
(3)如果有40人,那么需要多少张这样的桌子拼起来?
31.一条线段把一个长方形分为两部分,4条线段最多能把一个长方形分成几部分?20条呢?
32.一种细胞在培养过程中,每30分钟要分裂一次(1个母细胞一分为二成2个子细胞)。这种细胞如果要由1个分裂成8个,需要多少分钟?(请用画图的方法解释说明)
/ 让教学更有效 精品试卷 | 数学学科
/ 让教学更有效 精品试卷 | 数学学科
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.局
【分析】8个选手进行乒乓球单循环赛,每个选手都要参加7场比赛,而且每人获胜局数各不相同,所以每人获胜的局数分别为0~7局,那么冠军胜了7局。
【详解】单循环赛,每个人都要和其余的每个人进行比赛;
8-1=7(场)
每个选手都要参加7场比赛,既然每人获胜局数各不相同,那么只能是0~7;
冠军的胜场数肯定是最大的,所以冠军胜了7局;
答:冠军胜了7局。
【点睛】本题考查的是体育比赛中的数学问题,单循环比赛,n个队伍,每个队伍要比n-1场。
2.(1)22人
(2)(2n+2)人
(3)39张
【分析】一张桌子可以坐4人,后面每增加一张桌子,增加2个人,即1张桌坐4人;2张桌子坐4+2×(2-1)=6(人);3张桌子坐4+2×(3-1)=8(人);……(1)10张桌子可坐4+2×(10-1)=22(人);(2)n张桌子可坐4+2×(n-1)=2n+2(人);(3)设坐80人需要x张桌子,求解x即可。
【详解】(1)4+2×(10-1)
=4+18
=22(人);
答:10张桌子可坐22人。
(2)4+2×(n-1)=2n+2(人);
答:n张桌子可坐2n+2人。
(3)设需要x张桌子
2x+2=80
2x=78
x=39
答:坐80人需要39张桌子。
【点睛】考查数与形的找规律问题的实际应用,解方程的应用。按照将形化为数字,拆解研究规律即可。
3.1
【分析】封闭型数阵图,线和是10,先求A,再求B,再求C。
【详解】A=
B=
【点睛】本题较为简单,根据数阵图的基本要求直接求解即可。
4.36=15+21
【详解】题目中“三角形数”的规律为1、3、6、10、15、21…“正方形数”的规律为1、4、9、16、25…,根据题目已知条件:从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.可得出最后结果 .
5.(7n+1)根
【详解】略
6.我认为明明发现的规律较好,对于较大的数更好计算。
【分析】聪聪和明明发现的规律都很正确,但是聪聪的计算相较而言麻烦一点,随着要求数位的增加,明明的计算更加简单一点。
【详解】1=1=
1+2=3=
1+2+3=6=
故1+2+3+…+n=
所以对于较大的数,相比明明发现的规律更好计算。
答:我认为明明发现的规律较好,对于较大的数更好计算。
【点睛】本题主要考查找规律。
7.(1)白:26个;黑:10个
(2)16
【分析】(1)第1个图形一共有(3×3)个小正方形,有1个黑色小正方形,有(3×3-1)个白色小正方形;
第2个图形一共有(3×4)个小正方形,有2个黑色小正方形,有(3×4-2)个白色小正方形;
第3个图形一共有(3×5)个小正方形,有3个黑色小正方形,有(3×3-3)个白色小正方形;
……
第n个图形一共有3(n+2)=(3n+6)个小正方形,有n个黑色小正方形,有3n+6-n=2n+6个白色小正方形;
(2)把白色小正方形的个数代入表示白色小正方形含有字母的式子,求出n的值即可。
【详解】(1)分析图形规律可知:
第n个图形小正方形的总个数:3(n+2)=3n+6
第n个图形黑色小正方形的个数:n个
第n个图形白色小正方形的个数:3n+6-n=2n+6
当n=10时,
白色小正方形的个数:2n+6=2×10+6=26(个)
黑色小正方形的个数:10个
答:第10个图形中白色小正方形有26个,黑色小正方形有10个。
(2)由题意可知,
2n+6=38
解:2n=38-6
2n=32
n=32÷2
n=16
答:如果某个图形中有38个白色小正方形,那么这个图形排在第16。
【点睛】分析图形找出图形变化的规律,并用含有字母的式子表示出规律是解答题目的关键。
8.46个
每均分一次,正方形的个数增加3个;均分n次,正方形的个数就增加3n个.
【详解】1+3×15=46(个)
9.
【分析】复合型数阵图问题,每块区域的数都重复了一次,利用数和、线和的关系进行求解。
【详解】如图,令;
已知a,b,c,d,e,f各自用了两次,计算数和,;
令,解得;
容易得出0+1+4+5=10,0+2+3+5=10,1+2+3+4=10,如图,合理构造,得出最后的填法。
【点睛】复合型数阵图较为复杂,需要将辐射型、闭合型数阵图的方法综合起来求解,最关键的还是判断每一块的重复次数。
10.168个
【分析】如图,在每一个2×3的长方形里面,都可以找到两个目标图形,所以数出2×3的长方形个数,乘2得到目标图形的个数。
【详解】如图所示:
每2行可以数出6个2×3的长方形,每两列也可以数出6个2×3的长方形;
(个)
(个)
答:可以数出168个如图所示的“凸”字形图形。
【点睛】本题考查的是图形计数问题,可以将数目标图形转化成比较容易数的长方形。
11.(1)② (2)③
12.见详解;37;1+4(n-1)
【分析】第1个图形,1个点;
第2个图形,5个点,5=1+4=1+4×(2-1);
第3个图形,9个点,9=1+4×2=1+4×(3-1);
第4个图形,13个点,13=1+4×3=1+4×(4-1);
……
第n个图形的点数是1+4(n-1)个;
据此规律解答。
【详解】第五个图形有(1+4×4)个点。
如图:
第n个方框里有1+4(n-1)个点。
当n=10时
1+4(n-1)
=1+4×(10-1)
=1+4×9
=1+36
=37(个)
第10个方框里有37个点,第n个方框里有1+4(n-1)个点。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
13.(1)16张;(2)(10+2n)厘米.
【详解】(1)由图可知:第(1)个图形的小正方形卡纸个数为3×3-1,第(2)个图形的个数为3×4-2,第(3)个图形的个数为3×5-3,像这样拼下去,第(5)个图形用3×7-5=16张小正方形卡纸.
(2)第n个图形周长=(3+2+n)×2=10+2n(厘米)
14.①36个
②13个
【分析】①根据题图可知,第一个图形下层放2个,有4个三角形,第二个图形下层放3个,有9个三角形,第三个图形下层放4个,有16个三角形,据此可知,三角形的个数是下层放的个数的平方,当下层放6个时,则有6×6=36个小三角形;
②因为13×13=169,所以如果有169个三角形积木块,下层应放了13个,据此解答即可。
【详解】①6×6=36个;
答:如果下层放6个,一共需要36个三角形。
②13×13=169;
答:如果有169个三角形积木块,下层应放了13个。
【点睛】根据已知图形找到底层个数与三角形总个数的关系是解答本题的关键。
15.第四幅图有16个,第五幅有25个.
根据图意,第一幅点子的个数是12个.第二幅图是22个点子排成的正方形,第三幅图是32个点子,因此第四幅图是42个点子排成的正方形,第五幅图是52个点子排成的正方形,如图.
第四幅图是 ,第五幅图
【详解】略
16.根据题干中的已知图形中点数特点,可以探索出这组图形的一般规律,并利用规律进行解答.
观察图形可得:第一个图形有1个点,可以写作1+(1-1)×4;
第二个图形有1+4(个)点,可以写作1+(2-1)×4;
第三个图形有1+4+4(个)点,可以写作1+(3-1)×4……
则第n个图形的点数就可以写作1+(n-1)×4.
当n=6时,点数为1+(6-1)×4=21(个)
【详解】略
17.
由图可以看出淘淘一共握了两次手,分别是与龙一鸣和黄霏霏握的.
【解析】略
18.368
【分析】由图中可知:每行的末尾是行数的平方,下一行数的第一个数等于上一行末尾的数加1。
第一行的末尾是1的平方,第二行的末尾是2的平方是4;第三行的末尾是3的平方是9;第四行的末尾是4的平方是16;以此类推,第19行的末尾是19的平方是361,第20行末尾的数是20的平方是400;据此解答。
【详解】由分析可得:第19行的末尾是19的平方是361。
所以第20行的第一个数是361+1=362
那么,第7个数是362+(7-1)=368
答:第20行第7个是368。
【点睛】本题考查了数字排列的关系,此题的关键是要理解每行的末尾是行数的平方,下一行数的第一个数等于上一行末尾的数加1。
19.1
【详解】
从图上可以看出这些分数不断加下去,总和就是一
20.
【分析】把1换成,利用分数的基本性质,分子分母同时乘一个数,值不变,把化成,化成,化成,即可看出规律,对应第n项,分子等于n+1,分母等于2n因此得解。
【详解】将原数列变为…由此得出分子为n+1,分母为2n(n为第几个数),所以第2011个分数为,化简得。
【点睛】主要考查探索规律的实际能力,关键是先找出规律,然后根据规律写出第2011个分数,根据这个可以直接解答,注意解答的准确性。
21.(1)12;16;20;24 (2) 16块 (3) (4n+4)块
【详解】(2)(20÷4-1)×(20÷4-1)=16(块)
答:白瓷砖用了16块。
(3)n2=n×n,(n+1)×4=4n+4(块)。
答:花瓷砖用了(4n+4)块。
22.(1)14把;
(2)2n+2;
(3)16张
【分析】由图可知,1张桌子时,可以摆4把椅子;2张桌子时,可以摆(4+2)把椅子;3张桌子时,可以摆(4+2+2)把椅子……每增加一张桌子就增加2把椅子,那么n张桌子时,可以摆4+2(n-1)把椅子;最后计算出椅子数量为34时,n的值即可。
【详解】(1)1张桌子可以摆椅子的数量:4把
2张桌子可以摆椅子的数量:4+2=6(把)
3张桌子可以摆椅子的数量:4+2×2=4+4=8(把)
4张桌子可以摆椅子的数量:4+3×2=4+6=10(把)
5张桌子可以摆椅子的数量:4+4×2=4+8=12(把)
6张桌子可以摆椅子的数量:4+5×2=4+10=14(把)
答:6张桌子可以摆14把椅子。
(2)分析可知,n张桌子可以摆椅子的数量:4+2(n-1)=4+2n-2=(2n+2)把
(3)如果有34人,那么需要34把椅子。
2n+2=34
解:2n=34-2
2n=32
n=32÷2
n=16
答:如果有34人,需要并起来16张桌子才能坐下。
【点睛】分析题意找出椅子数量变化的规律是解答题目的关键。
23.19个
【分析】每列的和最少为0,最多是10,每行的和最少是0,最多是19,所以不同的和最多也就是0,1,2,3,4,…,18,19这20个。
【详解】首先每列的和最少为0,最多是10,每行的和最少是0,最多是19,所以不同的和最多也就是0,1,2,3,4,…,18,19这20个。如果和是0出现,那么必然有另外一个数字不能出现。如果0出现在行的和中,说明有1行全是0,意味着列的和中至多出现0到9,加上行的和至多出现10个数字,所以少了一种可能。如果0出现在列的和中,说明在行的和中19不可能出现,所以0出现就意味着另一个数字不能出现,所以至多是19。如下图所示:
除去重复的和,所以和最多是19个。
答: 最多能得到19个不同的和数。
【点睛】我们先弄清楚题意,分行分列的分别求出和,最后算出不同和的个数,综合考虑此题中最小和是0,最大和是19。假设每一行全写0则和是0,写上1个1则和是1,以此类推可得出最多的和的个数是19个。
24.(1)1个;3个;6个;10个;
(2)21个;45个;
(3)见详解;(1+2+3+4+…+n)个;
(4)55个
【分析】从图中可知:
(1)有1个三角形;
有2个小三角形和1个大三角形,一共是2+1=3(个)三角形;
有3个小三角形,相邻2个小三角形组成2个三角形,有1个大三角形,共有3+2+1=6(个)三角形;
有4个小三角形,相邻2个小三角形组成3个三角形,相邻3个小三角形组成2个三角形,有1个大三角形,共有4+3+2+1=10(个)三角形;
(2)按照这种规律画下去,
第6个图形:6+5+4+3+2+1=21(个)
第9个图形:9+8+7+6+5+4+3+2+1=45(个)
(3)由此得出规律:若图形中的单个小三角形个数为n,则图形中三角形的总个数就是(1+2+3+4+…+n)个。
(4)数出单个小三角形的个数,再按规律计算即可。
【详解】(1)1个
2+1=3(个)
3+2+1=6(个)
4+3+2+1=10(个)
答:第1个图形有1个三角形;第2个图形有3个三角形;第3个图形有6个三角形;第4个图形有10个三角形。
(2)第6个图形:6+5+4+3+2+1=21(个)
第9个图形:9+8+7+6+5+4+3+2+1=45(个)
答:第6个图形有21个三角形;第9个图形有45个三角形;
(3)答:我发现图中有几个小三角形就从1开始依次加到n。若图形中的单个小三角形个数为n,则图形中三角形的总个数就是(1+2+3+4+…+n)个。
(4)10+9+8+7+6+5+4+3+2+1=55(个)
答:图中一共有55个三角形。
25.41根
【详解】根据图示,
2间房:5+4=9(根)
3间房:5+4+4=13(根)
……
10间房:5+4×(10﹣1)=41(根)
答:搭10间房子,需要用41根小棒。
26.5;7;9;11;13
发现:火柴棒的根数=三角形的个数×2+1
【详解】略
27.234
【分析】观察数列可知,数列是按照1,3,5,7,9 循环进行排列的,先求出一组的和是多少,然后再求出前48个数共有多少组,余数是几就从左向右数几,然后相加即可。
【详解】1+3+5+7+9
=4+5+7+9
=9+7+9
=16+9
=25
48÷5=9(组) 3(个)
25×9+1+3+5
=225+1+3+5
=226+3+5
=229+5
=234
答:前48个数之和是234。
【点睛】本题考查循环数列,明确共有几个循环是解题的关键。
28.(1)1-40%-16%-20%-18%=6% 支付宝
(2)使用财付通支付的最少等.(答案不唯一)
(3)现在购物的支付方式越来越多,用现金支付的人逐渐减少.(答案不唯一,合理即可)
【解析】略
29.朝上,翻动偶数次与原来状态相同,翻动奇数次与原来状态相反
【详解】由题意可知:杯子翻动杯子1次,杯口朝下,翻动2次杯口朝上,翻动3次,杯口朝下,翻动4次,杯口朝上…,得出:翻动偶数次与原来状态相同,翻动奇数次与原来状态相反;
因为56是偶数;
所以翻动56次,杯口朝上.
答:翻动56次,杯口朝上.
30.(1)4×2+2=10(人)
(2)6×2+2=14(人)
(3)(40-2)÷2=19(张)
【解析】略
31.11部分,211部分
【分析】1条线段以后的规律:分成的部分=2+2+3+……+线段条数,由此根据规律计算即可.
【详解】
1条线段把长方形分为2部分.2
2条线段把长方形分为4部分,使分得的部分在原来的基础上增加了2部分.
3条线段把长方形分为7部分,使分得的部分在原来的基础上增加了3部分.
4条线段把长方形分成2+2+3+4=11部分.
20条线段就把长方形分成2+2+3+…+20=211部分.
答:4条最多能把一个长方形分成11部分,20条最对能分成211部分.
32.90分钟
【分析】一个细胞经过30分钟分裂成2个细胞,2个细胞经过30分钟分裂成4个细胞,4个细胞经过30分钟分裂成8个细胞,据此解答。
【详解】画图如下。
30×3=90(分钟)
答:需要90分钟。
【点睛】解决此题的关键是确定一个母细胞分裂成8个子细胞需要分裂的次数。
答案第1页,共2页
答案第1页,共2页
