人教版四年级下册数学三角形内角和(课件)(共24张PPT)
文档属性
| 名称 | 人教版四年级下册数学三角形内角和(课件)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-20 00:00:00 | ||
图片预览


文档简介
(共24张PPT)
三角形的内角和
R·四年级下册
一、故事导入
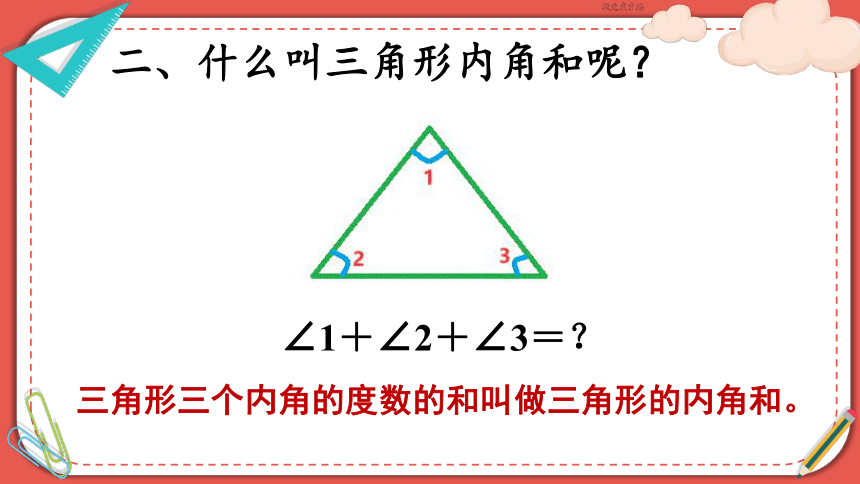
二、什么叫三角形内角和呢?
∠1+∠2+∠3=?
三角形三个内角的度数的和叫做三角形的内角和。
所有三角形的内角和都是180°吗
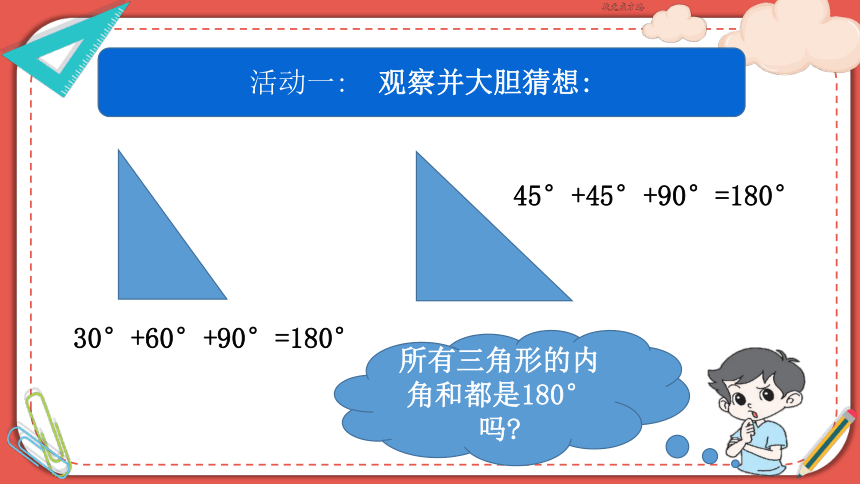
活动一: 观察并大胆猜想:
30°+60°+90°=180°
45°+45°+90°=180°
活动二: 1、测量法
请你在草稿本上画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度?开始吧!
合作探究
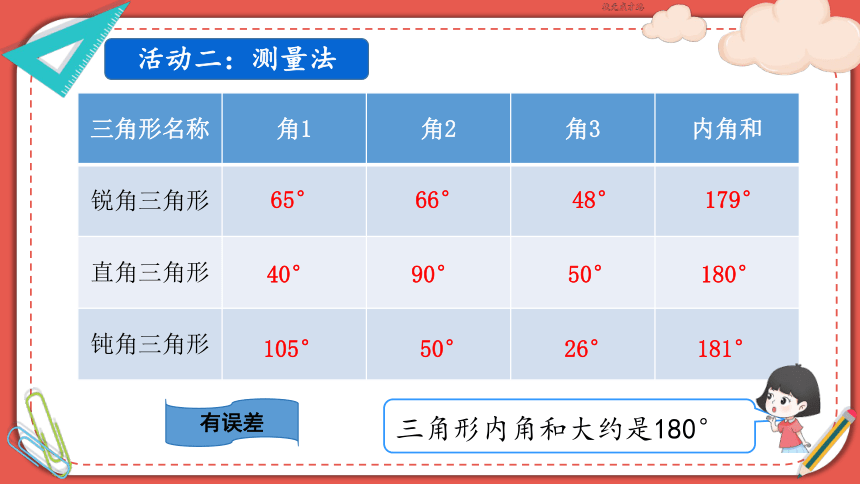
活动二:测量法
三角形名称 角1 角2 角3 内角和
锐角三角形
直角三角形
钝角三角形
65° 66° 48° 179°
40° 90° 50° 180°
105° 50° 26° 181°
三角形内角和大约是180°
有误差
三、合作探究
活动三:实验验证
1. 180°让你想起了我们学过
的什么角?
2. 我们能不能把三角形的
内角变成一个平角呢?
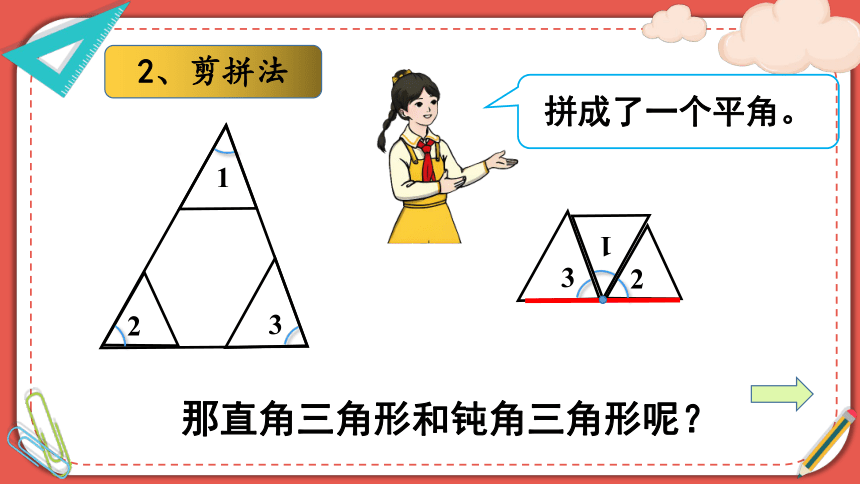
2、剪拼法
2
1
3
拼成了一个平角。
那直角三角形和钝角三角形呢?
1
3
2
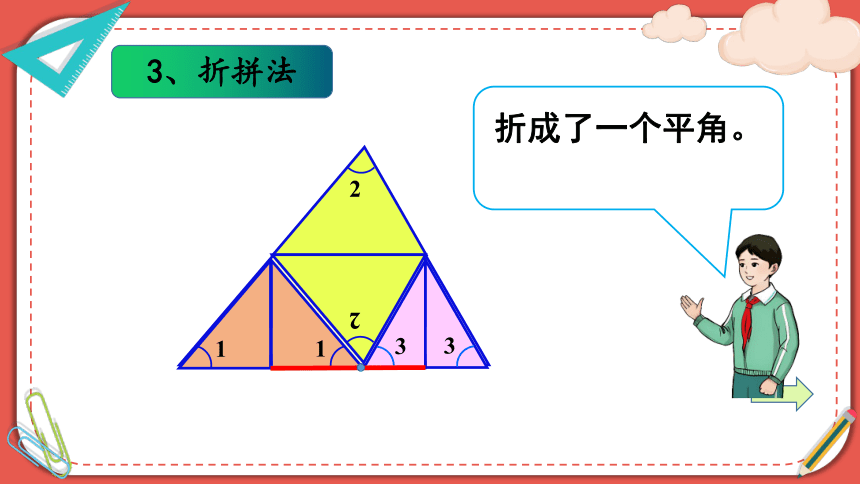
3、折拼法
1
3
1
3
折成了一个平角。
2
2
平角度数为180 °
三角形的三个角都拼成平角
三角形内角和为180 °
转化
180°-70°×2
答:风筝的顶角是 40°。
问:爸爸给小红买了一个等腰三角形的风筝。
风筝的一个底角是70°,风筝的顶角是多少度?
四、巩固运用
=180°-140°
=40°
5.三角形
五、课堂小结
三角形的内角和
测量法
剪拼法
折拼法
转化
三角形的内角和是180 °。
1、算等边三角形和等腰三角形的内角度数;
2、感知剪下的小三角形内角和还是180°;
3、生活中的数学。
六、作业练习
教 学 阐 述
一、教材分析
“三角形内角和”是“空间与图形”领域的重要内容之一。
在此之前,学生已经掌握了三角形的概念、分类,熟悉了锐角、直角、钝角、平角这些角的知识。所以本课的重点不在于了解,而在于验证和应用,同时发展学生的空间观念和思维能力、解决问题的能力。
二、学情分析
本节课的授课对象是四年级的学生,从心理特征来说,他们对于新鲜的知识充满着好奇心和强烈的求知欲望。
从认知状况来说,学生在此之前已经学习了三角形有关的知识,对三角形的内角已经有了初步的认识,这为顺利完成本节课的教学任务打下了基础。
三、教学目标
1、通过量、剪、拼等活动,发现并验证三角形的内角和是180°。
2、在学生动手获取知识的过程中,渗透“转化”的数学思想,培养学生的创新意识、实践能力和运用新知识解决问题的能力。
3、在探究过程中积累数学活动经验,激发学习数学的兴趣。
五、教法学法
本节课,我准备引导学生采用自主探究、动手操作、猜想验证、合作交流的学习方法,组织讨论,适时地启发帮助。使教法和学法统一在“以学生的发展为本"这一教育目标之中。
四、教学重难点:
教学重点:通过探索活动,发现“三角形三个内角和等于180”的规律。
教学难点:验证三角形的内角和等于180°。
六、教学过程
我以导入、猜测、验证、总结四个活动环节为主线,让学生通过自主探究进行数学的思考过程,积累数学活动经验。
(一)动画导入,提出问题
我是设计动画故事出示“三兄弟的内角和争吵"引入新知。引发学生猜想,质疑,引出课题。
【设计意图】:由“三兄弟的内角和”争吵,激趣导入,揭示并板书课题。随后引导学生质疑课题,让孩子们对新知产生浓烈的好奇心,激发学生学习内驱力,从被动学习转为主动学习,让课堂更加高效。
六、教学过程
(二)猜想验证,探究新知
活动一:猜想三角形的内角和
1、出示一副直角三角尺,让学生观察,算一算它们的内角和。
2、根据特殊三角尺的内角和,大胆猜想:所有三角形的内角和都是180°吗
【设计意图】:一副直角三角尺各内角的大小是学生已有的知识基础,从特殊的三角尺内角和是180°引发猜想,抓住学生最近发展区,有效联系了新旧知识。
六、教学过程
活动二 :测量并计算三角形的内角和
1、要研究多少三角形的内角和 确定分类研究后,学生分小组合作测量、计算。然后组织汇报。
【设计意图】:猜想,测量,学生自己经历三角形内角和的发现过程,不仅培养了学生的合作能力和动手操作能力,还在交流、质疑中培养优良学习品质。
六、教学过程
活动三:实验验证三角形的内角和
1、180度让你想起了我们学过的什么角
2、我们能不能把三角形的内角和变成一个平角呢
学生动手撕拼,将三角形的内角和转化成平角,验证三角形的内角和180°。课件展示用折、拼的方法将三角形的内角和转化成平角。
【设计意图】:用撕一撕、拼一拼的方法验证三角形的内角和是180°是本节课的难点,也是渗透转化思想方法的重要环节。紧扣学生已有知识引导思考“180°想起了什么角?”有效的激发学生思考,成功地将内角和180度与平角勾连,从而让学生顺利转化。
六、教学过程
(三)巩固练习,知识内化
出示学习单:
第一关:书上做一做计算三角形的一个内角;
第二关:让学生感知剪下的小三角形内角和还是180°;
第三关:算等边三角形和等腰三角形的内角度数;
第四关:生活中的数学。
【设计意图】:这样练习的设计注重层次性、基础性和思维性,既关注知识的灵活运用又关注空间观念的培养。
六、教学过程
(四)课堂回顾,总结收获。
1.同学们,通过这节课的学习,你有哪些收获
【设计意图】:引导学生谈收获,既关注知识的掌握,也关注学习方法的积累和运用。
谢 谢 聆 听
三角形的内角和
R·四年级下册
一、故事导入
二、什么叫三角形内角和呢?
∠1+∠2+∠3=?
三角形三个内角的度数的和叫做三角形的内角和。
所有三角形的内角和都是180°吗
活动一: 观察并大胆猜想:
30°+60°+90°=180°
45°+45°+90°=180°
活动二: 1、测量法
请你在草稿本上画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度?开始吧!
合作探究
活动二:测量法
三角形名称 角1 角2 角3 内角和
锐角三角形
直角三角形
钝角三角形
65° 66° 48° 179°
40° 90° 50° 180°
105° 50° 26° 181°
三角形内角和大约是180°
有误差
三、合作探究
活动三:实验验证
1. 180°让你想起了我们学过
的什么角?
2. 我们能不能把三角形的
内角变成一个平角呢?
2、剪拼法
2
1
3
拼成了一个平角。
那直角三角形和钝角三角形呢?
1
3
2
3、折拼法
1
3
1
3
折成了一个平角。
2
2
平角度数为180 °
三角形的三个角都拼成平角
三角形内角和为180 °
转化
180°-70°×2
答:风筝的顶角是 40°。
问:爸爸给小红买了一个等腰三角形的风筝。
风筝的一个底角是70°,风筝的顶角是多少度?
四、巩固运用
=180°-140°
=40°
5.三角形
五、课堂小结
三角形的内角和
测量法
剪拼法
折拼法
转化
三角形的内角和是180 °。
1、算等边三角形和等腰三角形的内角度数;
2、感知剪下的小三角形内角和还是180°;
3、生活中的数学。
六、作业练习
教 学 阐 述
一、教材分析
“三角形内角和”是“空间与图形”领域的重要内容之一。
在此之前,学生已经掌握了三角形的概念、分类,熟悉了锐角、直角、钝角、平角这些角的知识。所以本课的重点不在于了解,而在于验证和应用,同时发展学生的空间观念和思维能力、解决问题的能力。
二、学情分析
本节课的授课对象是四年级的学生,从心理特征来说,他们对于新鲜的知识充满着好奇心和强烈的求知欲望。
从认知状况来说,学生在此之前已经学习了三角形有关的知识,对三角形的内角已经有了初步的认识,这为顺利完成本节课的教学任务打下了基础。
三、教学目标
1、通过量、剪、拼等活动,发现并验证三角形的内角和是180°。
2、在学生动手获取知识的过程中,渗透“转化”的数学思想,培养学生的创新意识、实践能力和运用新知识解决问题的能力。
3、在探究过程中积累数学活动经验,激发学习数学的兴趣。
五、教法学法
本节课,我准备引导学生采用自主探究、动手操作、猜想验证、合作交流的学习方法,组织讨论,适时地启发帮助。使教法和学法统一在“以学生的发展为本"这一教育目标之中。
四、教学重难点:
教学重点:通过探索活动,发现“三角形三个内角和等于180”的规律。
教学难点:验证三角形的内角和等于180°。
六、教学过程
我以导入、猜测、验证、总结四个活动环节为主线,让学生通过自主探究进行数学的思考过程,积累数学活动经验。
(一)动画导入,提出问题
我是设计动画故事出示“三兄弟的内角和争吵"引入新知。引发学生猜想,质疑,引出课题。
【设计意图】:由“三兄弟的内角和”争吵,激趣导入,揭示并板书课题。随后引导学生质疑课题,让孩子们对新知产生浓烈的好奇心,激发学生学习内驱力,从被动学习转为主动学习,让课堂更加高效。
六、教学过程
(二)猜想验证,探究新知
活动一:猜想三角形的内角和
1、出示一副直角三角尺,让学生观察,算一算它们的内角和。
2、根据特殊三角尺的内角和,大胆猜想:所有三角形的内角和都是180°吗
【设计意图】:一副直角三角尺各内角的大小是学生已有的知识基础,从特殊的三角尺内角和是180°引发猜想,抓住学生最近发展区,有效联系了新旧知识。
六、教学过程
活动二 :测量并计算三角形的内角和
1、要研究多少三角形的内角和 确定分类研究后,学生分小组合作测量、计算。然后组织汇报。
【设计意图】:猜想,测量,学生自己经历三角形内角和的发现过程,不仅培养了学生的合作能力和动手操作能力,还在交流、质疑中培养优良学习品质。
六、教学过程
活动三:实验验证三角形的内角和
1、180度让你想起了我们学过的什么角
2、我们能不能把三角形的内角和变成一个平角呢
学生动手撕拼,将三角形的内角和转化成平角,验证三角形的内角和180°。课件展示用折、拼的方法将三角形的内角和转化成平角。
【设计意图】:用撕一撕、拼一拼的方法验证三角形的内角和是180°是本节课的难点,也是渗透转化思想方法的重要环节。紧扣学生已有知识引导思考“180°想起了什么角?”有效的激发学生思考,成功地将内角和180度与平角勾连,从而让学生顺利转化。
六、教学过程
(三)巩固练习,知识内化
出示学习单:
第一关:书上做一做计算三角形的一个内角;
第二关:让学生感知剪下的小三角形内角和还是180°;
第三关:算等边三角形和等腰三角形的内角度数;
第四关:生活中的数学。
【设计意图】:这样练习的设计注重层次性、基础性和思维性,既关注知识的灵活运用又关注空间观念的培养。
六、教学过程
(四)课堂回顾,总结收获。
1.同学们,通过这节课的学习,你有哪些收获
【设计意图】:引导学生谈收获,既关注知识的掌握,也关注学习方法的积累和运用。
谢 谢 聆 听
