人教版2024-2025学年四年级数学上册专项提升第二单元公顷和平方千米·思维素养篇【从课内到奥数】(原卷版+解析)
文档属性
| 名称 | 人教版2024-2025学年四年级数学上册专项提升第二单元公顷和平方千米·思维素养篇【从课内到奥数】(原卷版+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-20 10:38:41 | ||
图片预览




文档简介
目 录
【课内精选一】公顷和平方千米的实际应用(一) 3
【课内精选二】公顷和平方千米的实际应用(二) 4
【奥数拓展一】平移法求图形的周长(一) 5
【奥数拓展二】平移法求图形的周长(二) 6
【奥数拓展三】割补、平移或旋转法求图形的面积(一) 8
【奥数拓展四】割补、平移或旋转法求图形的面积(二) 9
人教版2024-2025学年四年级数学上册专项提升
第二单元公顷和平方千米·思维素养篇【从课内到奥数】
【课内精选一】公顷和平方千米的实际应用(一)。
牧场有一片长2000米、宽400米的草场,邻近有一个面积为1平方千米的湖泊与一个面积为10公顷的林场,请比较草场、湖泊与林场的大小。
【专项训练】
1.天安门广场是世界上最大的城市广场之一,面积大约是400000平方米,合多少公顷
2. 1平方千米等于多少公顷 5000公顷等于多少平方千米
3. 边长是200米的正方形土地面积是多少公顷
【课内精选二】公顷和平方千米的实际应用(二)。
一块边长为400米的正方形果园中,种植了8000棵果树,照这样计算,占地面积为15公顷的果园,能种植果树多少棵
【专项训练】
1.一块边长为400米的正方形果园中,种植了8000棵果树,照这样计算,一块边长为800米的正方形果园,能种植果树多少棵
2.建筑队计划在一条长40千米,宽20米的高架路面上铺设沥青,已知铺设1公顷地面需要50名工人工作一天,建筑队现有100名工人,完成这项任务需要多少天
3.一块占地4公顷的正方形苗圃,如果边长增加100米,那么苗圃的面积增加多少公顷
【奥数拓展一】平移法求图形的周长(一)。
一张边长是20厘米的正方形纸片,沿着正方形的边沿剪下一个边长是4厘米的正方形,剩下图形的周长是多少厘米
【专项训练】
1.计算下图的周长。(单位:厘米)
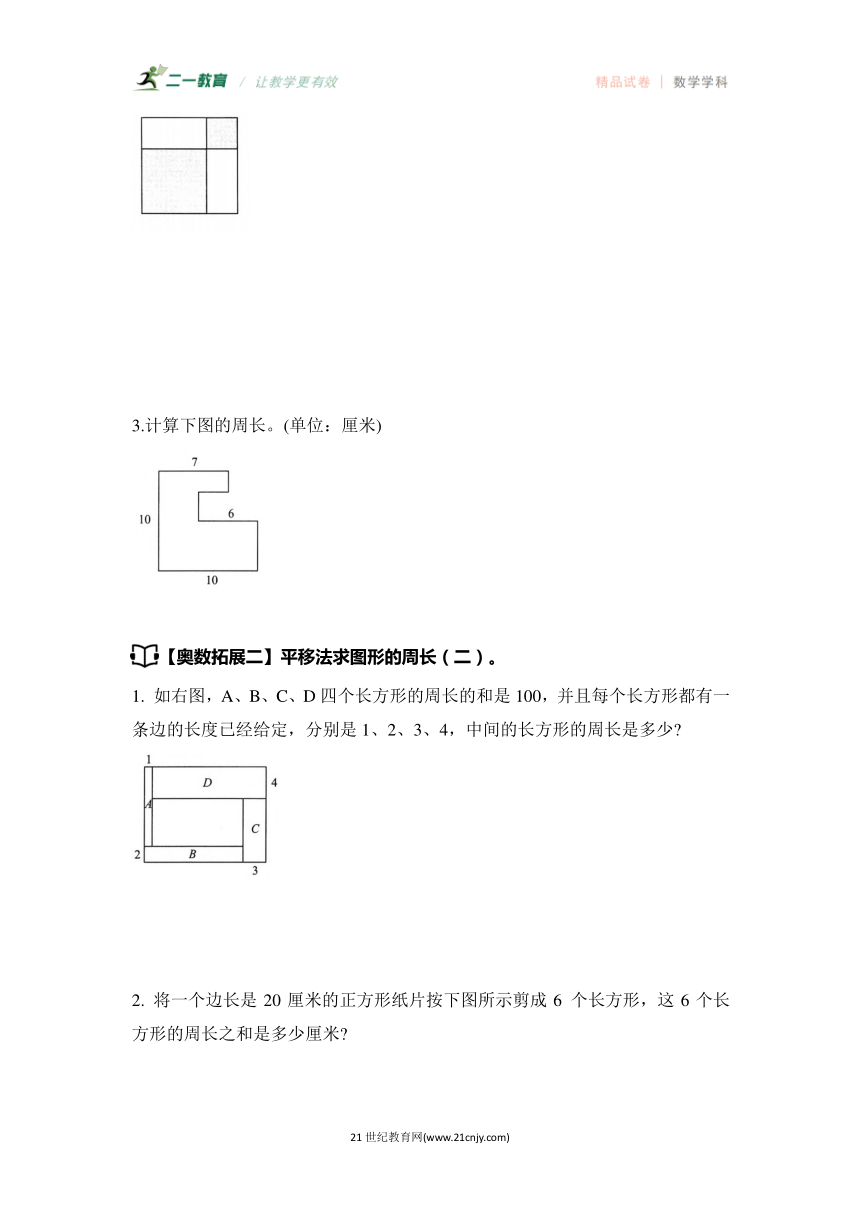
2.下图是一个大正方形,里面两个阴影部分是小正方形,已知两个小正方形的周长和是60厘米,那么每个白色长方形的周长是多少厘米
3.计算下图的周长。(单位:厘米)
【奥数拓展二】平移法求图形的周长(二)。
1. 如右图,A、B、C、D四个长方形的周长的和是100,并且每个长方形都有一条边的长度已经给定,分别是1、2、3、4,中间的长方形的周长是多少
2. 将一个边长是20厘米的正方形纸片按下图所示剪成6 个长方形,这6个长方形的周长之和是多少厘米
【专项训练】
1.如图是一张长为12厘米,宽为11厘米的长方形纸片,按照虚线将这张纸片剪为两部分,这两部分的周长之和是多少厘米
2.如下图,将大正方形分成了12个小长方形,这12个小长方形的周长比原正方形的周长长120厘米,那么大正方形的周长是多少厘米
3. 如图,一个长方形被分成4个小长方形,其中长方形A、B、C的周长分别是10 厘米、12厘米、14厘米,那么长方形D的周长是多少厘米
【奥数拓展三】割补、平移或旋转法求图形的面积(一)。
用同样大小的长方形小纸片,摆成了如图的形状,已知小纸片的宽度是12厘米,求阴影部分面积的和。
【专项训练】
1.如图,用5个小正方形和1个大正方形拼成一个更大的正方形,已知最大正方形的周长为120厘米,大正方形的面积是多少平方厘米
2.如图,六个相同的长方形围成了大、小两个正方形,已知小正方形的面积是36平方厘米,则每个小长方形的面积是多少平方厘米
3. 5个相同的长方形放在一个正方形内,所有长方形的边都平行于正方形的对应边,正方形的边长为24厘米,每个小长方形的面积是多少
【奥数拓展四】割补、平移或旋转法求图形的面积(二)。
1. 下图中所标的数为相应区域的面积,求阴影部分的面积。
2. 一张长方形纸片,在长边上剪下10厘米、宽边上剪下5厘米,余下的部分正 好是一个正方形,已知正方形面积比原长方形纸片面积少140平方厘米,求原长方形纸片的面积。
【专项训练】
1.计算长方形A、B、C、D的面积之和。(单位:平方厘米)
2.如图所示,在大长方形中放入六个形状大小相同的长方形,图中阴影部分的面积是多少
3.长方形ABCD的周长是14厘米,在它的每条边上各画一个以该边为边长的正 方形(如图),已知这四个正方形的面积和是50平方厘米,那么长方形ABCD的面积是多少平方厘米
21世纪教育网(www.21cnjy.com)
目 录
【课内精选一】公顷和平方千米的实际应用(一) 3
【课内精选二】公顷和平方千米的实际应用(二) 3
【奥数拓展一】平移法求图形的周长(一) 5
【奥数拓展二】平移法求图形的周长(二) 6
【奥数拓展三】割补、平移或旋转法求图形的面积(一) 8
【奥数拓展四】割补、平移或旋转法求图形的面积(二) 9
人教版2024-2025学年四年级数学上册专项提升
第二单元公顷和平方千米·思维素养篇【从课内到奥数】
【课内精选一】公顷和平方千米的实际应用(一)。
牧场有一片长2000米、宽400米的草场,邻近有一个面积为1平方千米的湖泊与一个面积为10公顷的林场,请比较草场、湖泊与林场的大小。
解析:先计算草场的面积,面积为2000×400=800000(平方米),再比较800000平方米、1平方千米与10公顷的大小,由于这三个量的单位各不相同,因此我们可以将1平方千米、10公顷转化为以平方米为单位的数,1平方千米= 1000000平方米,10公顷=100000平方米,那么1000000平方米>800000平方米>100000平方米,因此湖泊面积最大,草场其次,林场面积最小。
【专项训练】
1.天安门广场是世界上最大的城市广场之一,面积大约是400000平方米,合多少公顷
解析:40公顷。
2. 1平方千米等于多少公顷 5000公顷等于多少平方千米
解析:100公顷;50公顷
3. 边长是200米的正方形土地面积是多少公顷
解析:4公顷。
【课内精选二】公顷和平方千米的实际应用(二)。
一块边长为400米的正方形果园中,种植了8000棵果树,照这样计算,占地面积为15公顷的果园,能种植果树多少棵
解析:边长为400米的正方形果园面积为400×400=160000(平方米),合16 公顷,那么平均1公顷种植果树8000÷16=500(棵),因此15公顷土地能种植果树 500×15=7500(棵)。
【专项训练】
1.一块边长为400米的正方形果园中,种植了8000棵果树,照这样计算,一块边长为800米的正方形果园,能种植果树多少棵
解析:800÷400=2,2×2=4,边长为800米的正方形是边长为400米的正方形的面积的4倍,能种植果树8000×4=32000(棵)。
2.建筑队计划在一条长40千米,宽20米的高架路面上铺设沥青,已知铺设1公顷地面需要50名工人工作一天,建筑队现有100名工人,完成这项任务需要多少天
解析:40千米=40000米,高架路面面积为40000×20= 800000(平方米),合80公顷,100名工人工作1天能完成2公顷的铺设任务,所以完成任务共需要80÷2=40(天)。
3.一块占地4公顷的正方形苗圃,如果边长增加100米,那么苗圃的面积增加多少公顷
解析:4公顷=40000平方米=200米×200米,(200+ 100)×(200+100)=90000(平方米),90000平方米=9公顷,9-4=5(公顷)
【奥数拓展一】平移法求图形的周长(一)。
一张边长是20厘米的正方形纸片,沿着正方形的边沿剪下一个边长是4厘米的正方形,剩下图形的周长是多少厘米
解析:剪下一个边长是4厘米的正方形,有下列两种不同的剪法,对于图1的剪 法,我们只需将边长为4厘米的两条线段向上、向右平移,那么图1的周长就等于原来正方形的周长,是20×4=80(厘米);对于图2的剪法,我们可以将一条边长为4厘米的线段向上平移,那么图2的周长比原来正方形的周长多了两条小正方形的边长,即20×4+4×2=88(厘米)。
【专项训练】
1.计算下图的周长。(单位:厘米)
解析:(9+7+9)×2=50(厘米)
2.下图是一个大正方形,里面两个阴影部分是小正方形,已知两个小正方形的周长和是60厘米,那么每个白色长方形的周长是多少厘米
解析:每个白色长方形的长与宽的和为60÷4=15(厘米),每个白色长方形的周长为15×2=30(厘米)
3.计算下图的周长。(单位:厘米)
解析:
如下图所示,将图形中的线段平移,所求图形的周长可转化为一个边长为10厘米的正方形的周长加上两条长度为7+6—10=3(厘米)的线段,所求图形的周长为 10×4+3×2=46(厘米)。
【奥数拓展二】平移法求图形的周长(二)。
1. 如右图,A、B、C、D四个长方形的周长的和是100,并且每个长方形都有一条边的长度已经给定,分别是1、2、3、4,中间的长方形的周长是多少
解析:A、B、C、D四个长方形的周长之和相当于最大的长方形周长的2倍,最大的长方形周长是100÷2= 50,中间长方形的周长比最大长方形的周长少了2个1,2个2,2个3,2个4,所以中间长方形的周长为50—(1+2+ 3+4)×2=30。
2. 将一个边长是20厘米的正方形纸片按下图所示剪成6 个长方形,这6个长方形的周长之和是多少厘米
解析:要求这6个长方形的周长之和,如果按先算出每个小长方形的周长,再逐一相加求和的思路去解决问题是行不通的,因为每个长方形长与宽的尺寸都未知,因此我们可以换一个角度考虑问题,从整体上看,这6个长方形的周长之和比原来正方形的周长增加了6条正方形的边长(正方形被剪成了6个长方形,每剪1刀,增加2条正方形的边长,剪了3刀共增加6条正方形的边长),所以这6个长方形的周长之和为20×4+20×6=200(厘米)。
【专项训练】
1.如图是一张长为12厘米,宽为11厘米的长方形纸片,按照虚线将这张纸片剪为两部分,这两部分的周长之和是多少厘米
解析:
长方形周长为(12+11)× 2=46(厘米),两部分周长和相当于长方形的周长与中间那条折线长度的2倍之和,即46+11×2+ (12—4—3)×3×2=98(厘米)。
2.如下图,将大正方形分成了12个小长方形,这12个小长方形的周长比原正方形的周长长120厘米,那么大正方形的周长是多少厘米
解析:
12个小长方形的周长和比大正方形的周长多了5× 2=10(条)大正方形的边长,因此,大正方形的边长为120÷10=12(厘米),周长为12×4=48(厘米)。
3. 如图,一个长方形被分成4个小长方形,其中长方形A、B、C的周长分别是10 厘米、12厘米、14厘米,那么长方形D的周长是多少厘米
解析:
通过平移可以发现:长方形B、C的周长之和恰好等于大长方形的周长,同样长方形A、D的周长之和也等于大长方形的周长,所以长方形D的周长为12+ 14—10=16(厘米)。
【奥数拓展三】割补、平移或旋转法求图形的面积(一)。
用同样大小的长方形小纸片,摆成了如图的形状,已知小纸片的宽度是12厘米,求阴影部分面积的和。
解析;
由于5个小纸片的长=3个小纸片的宽+3个小纸片的长,即2个小纸片的长=3个小纸片的宽,又小纸片的宽=12厘米,所以2个小纸片的长=36厘米,即1个小纸片的长=18厘米。
因此,阴影部分的一个小正方形的边长为18—12=6(厘米),所以阴影部分的面积是3×36=108(平方厘米)。
【专项训练】
1.如图,用5个小正方形和1个大正方形拼成一个更大的正方形,已知最大正方形的周长为120厘米,大正方形的面积是多少平方厘米
解析:
大正方形的边长是小正方形边长的2倍,每个小正方形的边长为
120÷4÷(1+2)=10(厘米),大正方形的边长为10×2=20(厘米),大正方形的面积是 20×20=400(平方厘米)。
2.如图,六个相同的长方形围成了大、小两个正方形,已知小正方形的面积是36平方厘米,则每个小长方形的面积是多少平方厘米
解析:
小正方形的面积为36平方厘米,边长为6厘米,小长方形的长就是6厘米,2个宽+1个长=2个长,所以小长方形的宽=6÷2=3(厘米),每个小长方形的面积为6×3=18(平方厘米)。
3. 5个相同的长方形放在一个正方形内,所有长方形的边都平行于正方形的对应边,正方形的边长为24厘米,每个小长方形的面积是多少
解析:
从水平方向观察,通过平移,不难发现3个长方形的长=24厘米,则长为24÷3=8(厘米);从竖直方向观察,2条长+2条宽=24厘米,则宽为24÷2—8= 4(厘米),那么每个小长方形的面积为8×4=32(平方厘米)。
【奥数拓展四】割补、平移或旋转法求图形的面积(二)。
1. 下图中所标的数为相应区域的面积,求阴影部分的面积。
解析:
因为面积为9与面积为3的两个长方形的长相等,所以,面积为9的长方形宽是面积为3的长方形宽的9÷3=3倍,那么阴影部分的面积为7×3=21
2. 一张长方形纸片,在长边上剪下10厘米、宽边上剪下5厘米,余下的部分正 好是一个正方形,已知正方形面积比原长方形纸片面积少140平方厘米,求原长方形纸片的面积。
解析:
已知正方形面积比原长方形纸片面积少140平方厘米,从图中可以看出是长方形A、B、C的面积之和,由于余下的部分是一个正方形,所以长方形C的宽与长方形A的长相等,因此可以先算正方形边长,正方形边长=(140— 10×5)÷(5+10)=6(厘米),那么原长方形纸片面积为140+ 6×6=176(平方厘米)
【专项训练】
1.计算长方形A、B、C、D的面积之和。(单位:平方厘米)
解析:
C的面积为20×24÷30=16(平方厘米);
A的面积为20×8÷16=10(平方厘米);
B的面积为6×16÷8=12(平方厘米);
D的面积为24×12÷16=18(平方厘米),A+B+C+D=10+12+16+18=56(平方厘米)。
2.如图所示,在大长方形中放入六个形状大小相同的长方形,图中阴影部分的面积是多少
解析:
设小长方形的长边为a,短边为b,从水平方向观察可知:a+36=14;从垂直方向观察可知:2b+6=a+ b,即a =b+6,将a=b+6代入a+3b=14中,可得
b=(14—6)÷(3+1)=2,a=2+6=8,大长方形的长为14,宽为6+2×2=10,阴影部分面积为14×10—8×2×6=44
3.长方形ABCD的周长是14厘米,在它的每条边上各画一个以该边为边长的正 方形(如图),已知这四个正方形的面积和是50平方厘米,那么长方形ABCD的面积是多少平方厘米
解析:
如图所示,将长方形DFGH补在原图右上角,得到正方形BEGI,它的边长等于14÷2=7(厘米),又因为正方形ADHI与CEFD的面积和为50÷2= 25(平方厘米),所以长方形ABCD的面积为:(7×7—25)÷2=12(平方厘米)
21世纪教育网(www.21cnjy.com)
【课内精选一】公顷和平方千米的实际应用(一) 3
【课内精选二】公顷和平方千米的实际应用(二) 4
【奥数拓展一】平移法求图形的周长(一) 5
【奥数拓展二】平移法求图形的周长(二) 6
【奥数拓展三】割补、平移或旋转法求图形的面积(一) 8
【奥数拓展四】割补、平移或旋转法求图形的面积(二) 9
人教版2024-2025学年四年级数学上册专项提升
第二单元公顷和平方千米·思维素养篇【从课内到奥数】
【课内精选一】公顷和平方千米的实际应用(一)。
牧场有一片长2000米、宽400米的草场,邻近有一个面积为1平方千米的湖泊与一个面积为10公顷的林场,请比较草场、湖泊与林场的大小。
【专项训练】
1.天安门广场是世界上最大的城市广场之一,面积大约是400000平方米,合多少公顷
2. 1平方千米等于多少公顷 5000公顷等于多少平方千米
3. 边长是200米的正方形土地面积是多少公顷
【课内精选二】公顷和平方千米的实际应用(二)。
一块边长为400米的正方形果园中,种植了8000棵果树,照这样计算,占地面积为15公顷的果园,能种植果树多少棵
【专项训练】
1.一块边长为400米的正方形果园中,种植了8000棵果树,照这样计算,一块边长为800米的正方形果园,能种植果树多少棵
2.建筑队计划在一条长40千米,宽20米的高架路面上铺设沥青,已知铺设1公顷地面需要50名工人工作一天,建筑队现有100名工人,完成这项任务需要多少天
3.一块占地4公顷的正方形苗圃,如果边长增加100米,那么苗圃的面积增加多少公顷
【奥数拓展一】平移法求图形的周长(一)。
一张边长是20厘米的正方形纸片,沿着正方形的边沿剪下一个边长是4厘米的正方形,剩下图形的周长是多少厘米
【专项训练】
1.计算下图的周长。(单位:厘米)
2.下图是一个大正方形,里面两个阴影部分是小正方形,已知两个小正方形的周长和是60厘米,那么每个白色长方形的周长是多少厘米
3.计算下图的周长。(单位:厘米)
【奥数拓展二】平移法求图形的周长(二)。
1. 如右图,A、B、C、D四个长方形的周长的和是100,并且每个长方形都有一条边的长度已经给定,分别是1、2、3、4,中间的长方形的周长是多少
2. 将一个边长是20厘米的正方形纸片按下图所示剪成6 个长方形,这6个长方形的周长之和是多少厘米
【专项训练】
1.如图是一张长为12厘米,宽为11厘米的长方形纸片,按照虚线将这张纸片剪为两部分,这两部分的周长之和是多少厘米
2.如下图,将大正方形分成了12个小长方形,这12个小长方形的周长比原正方形的周长长120厘米,那么大正方形的周长是多少厘米
3. 如图,一个长方形被分成4个小长方形,其中长方形A、B、C的周长分别是10 厘米、12厘米、14厘米,那么长方形D的周长是多少厘米
【奥数拓展三】割补、平移或旋转法求图形的面积(一)。
用同样大小的长方形小纸片,摆成了如图的形状,已知小纸片的宽度是12厘米,求阴影部分面积的和。
【专项训练】
1.如图,用5个小正方形和1个大正方形拼成一个更大的正方形,已知最大正方形的周长为120厘米,大正方形的面积是多少平方厘米
2.如图,六个相同的长方形围成了大、小两个正方形,已知小正方形的面积是36平方厘米,则每个小长方形的面积是多少平方厘米
3. 5个相同的长方形放在一个正方形内,所有长方形的边都平行于正方形的对应边,正方形的边长为24厘米,每个小长方形的面积是多少
【奥数拓展四】割补、平移或旋转法求图形的面积(二)。
1. 下图中所标的数为相应区域的面积,求阴影部分的面积。
2. 一张长方形纸片,在长边上剪下10厘米、宽边上剪下5厘米,余下的部分正 好是一个正方形,已知正方形面积比原长方形纸片面积少140平方厘米,求原长方形纸片的面积。
【专项训练】
1.计算长方形A、B、C、D的面积之和。(单位:平方厘米)
2.如图所示,在大长方形中放入六个形状大小相同的长方形,图中阴影部分的面积是多少
3.长方形ABCD的周长是14厘米,在它的每条边上各画一个以该边为边长的正 方形(如图),已知这四个正方形的面积和是50平方厘米,那么长方形ABCD的面积是多少平方厘米
21世纪教育网(www.21cnjy.com)
目 录
【课内精选一】公顷和平方千米的实际应用(一) 3
【课内精选二】公顷和平方千米的实际应用(二) 3
【奥数拓展一】平移法求图形的周长(一) 5
【奥数拓展二】平移法求图形的周长(二) 6
【奥数拓展三】割补、平移或旋转法求图形的面积(一) 8
【奥数拓展四】割补、平移或旋转法求图形的面积(二) 9
人教版2024-2025学年四年级数学上册专项提升
第二单元公顷和平方千米·思维素养篇【从课内到奥数】
【课内精选一】公顷和平方千米的实际应用(一)。
牧场有一片长2000米、宽400米的草场,邻近有一个面积为1平方千米的湖泊与一个面积为10公顷的林场,请比较草场、湖泊与林场的大小。
解析:先计算草场的面积,面积为2000×400=800000(平方米),再比较800000平方米、1平方千米与10公顷的大小,由于这三个量的单位各不相同,因此我们可以将1平方千米、10公顷转化为以平方米为单位的数,1平方千米= 1000000平方米,10公顷=100000平方米,那么1000000平方米>800000平方米>100000平方米,因此湖泊面积最大,草场其次,林场面积最小。
【专项训练】
1.天安门广场是世界上最大的城市广场之一,面积大约是400000平方米,合多少公顷
解析:40公顷。
2. 1平方千米等于多少公顷 5000公顷等于多少平方千米
解析:100公顷;50公顷
3. 边长是200米的正方形土地面积是多少公顷
解析:4公顷。
【课内精选二】公顷和平方千米的实际应用(二)。
一块边长为400米的正方形果园中,种植了8000棵果树,照这样计算,占地面积为15公顷的果园,能种植果树多少棵
解析:边长为400米的正方形果园面积为400×400=160000(平方米),合16 公顷,那么平均1公顷种植果树8000÷16=500(棵),因此15公顷土地能种植果树 500×15=7500(棵)。
【专项训练】
1.一块边长为400米的正方形果园中,种植了8000棵果树,照这样计算,一块边长为800米的正方形果园,能种植果树多少棵
解析:800÷400=2,2×2=4,边长为800米的正方形是边长为400米的正方形的面积的4倍,能种植果树8000×4=32000(棵)。
2.建筑队计划在一条长40千米,宽20米的高架路面上铺设沥青,已知铺设1公顷地面需要50名工人工作一天,建筑队现有100名工人,完成这项任务需要多少天
解析:40千米=40000米,高架路面面积为40000×20= 800000(平方米),合80公顷,100名工人工作1天能完成2公顷的铺设任务,所以完成任务共需要80÷2=40(天)。
3.一块占地4公顷的正方形苗圃,如果边长增加100米,那么苗圃的面积增加多少公顷
解析:4公顷=40000平方米=200米×200米,(200+ 100)×(200+100)=90000(平方米),90000平方米=9公顷,9-4=5(公顷)
【奥数拓展一】平移法求图形的周长(一)。
一张边长是20厘米的正方形纸片,沿着正方形的边沿剪下一个边长是4厘米的正方形,剩下图形的周长是多少厘米
解析:剪下一个边长是4厘米的正方形,有下列两种不同的剪法,对于图1的剪 法,我们只需将边长为4厘米的两条线段向上、向右平移,那么图1的周长就等于原来正方形的周长,是20×4=80(厘米);对于图2的剪法,我们可以将一条边长为4厘米的线段向上平移,那么图2的周长比原来正方形的周长多了两条小正方形的边长,即20×4+4×2=88(厘米)。
【专项训练】
1.计算下图的周长。(单位:厘米)
解析:(9+7+9)×2=50(厘米)
2.下图是一个大正方形,里面两个阴影部分是小正方形,已知两个小正方形的周长和是60厘米,那么每个白色长方形的周长是多少厘米
解析:每个白色长方形的长与宽的和为60÷4=15(厘米),每个白色长方形的周长为15×2=30(厘米)
3.计算下图的周长。(单位:厘米)
解析:
如下图所示,将图形中的线段平移,所求图形的周长可转化为一个边长为10厘米的正方形的周长加上两条长度为7+6—10=3(厘米)的线段,所求图形的周长为 10×4+3×2=46(厘米)。
【奥数拓展二】平移法求图形的周长(二)。
1. 如右图,A、B、C、D四个长方形的周长的和是100,并且每个长方形都有一条边的长度已经给定,分别是1、2、3、4,中间的长方形的周长是多少
解析:A、B、C、D四个长方形的周长之和相当于最大的长方形周长的2倍,最大的长方形周长是100÷2= 50,中间长方形的周长比最大长方形的周长少了2个1,2个2,2个3,2个4,所以中间长方形的周长为50—(1+2+ 3+4)×2=30。
2. 将一个边长是20厘米的正方形纸片按下图所示剪成6 个长方形,这6个长方形的周长之和是多少厘米
解析:要求这6个长方形的周长之和,如果按先算出每个小长方形的周长,再逐一相加求和的思路去解决问题是行不通的,因为每个长方形长与宽的尺寸都未知,因此我们可以换一个角度考虑问题,从整体上看,这6个长方形的周长之和比原来正方形的周长增加了6条正方形的边长(正方形被剪成了6个长方形,每剪1刀,增加2条正方形的边长,剪了3刀共增加6条正方形的边长),所以这6个长方形的周长之和为20×4+20×6=200(厘米)。
【专项训练】
1.如图是一张长为12厘米,宽为11厘米的长方形纸片,按照虚线将这张纸片剪为两部分,这两部分的周长之和是多少厘米
解析:
长方形周长为(12+11)× 2=46(厘米),两部分周长和相当于长方形的周长与中间那条折线长度的2倍之和,即46+11×2+ (12—4—3)×3×2=98(厘米)。
2.如下图,将大正方形分成了12个小长方形,这12个小长方形的周长比原正方形的周长长120厘米,那么大正方形的周长是多少厘米
解析:
12个小长方形的周长和比大正方形的周长多了5× 2=10(条)大正方形的边长,因此,大正方形的边长为120÷10=12(厘米),周长为12×4=48(厘米)。
3. 如图,一个长方形被分成4个小长方形,其中长方形A、B、C的周长分别是10 厘米、12厘米、14厘米,那么长方形D的周长是多少厘米
解析:
通过平移可以发现:长方形B、C的周长之和恰好等于大长方形的周长,同样长方形A、D的周长之和也等于大长方形的周长,所以长方形D的周长为12+ 14—10=16(厘米)。
【奥数拓展三】割补、平移或旋转法求图形的面积(一)。
用同样大小的长方形小纸片,摆成了如图的形状,已知小纸片的宽度是12厘米,求阴影部分面积的和。
解析;
由于5个小纸片的长=3个小纸片的宽+3个小纸片的长,即2个小纸片的长=3个小纸片的宽,又小纸片的宽=12厘米,所以2个小纸片的长=36厘米,即1个小纸片的长=18厘米。
因此,阴影部分的一个小正方形的边长为18—12=6(厘米),所以阴影部分的面积是3×36=108(平方厘米)。
【专项训练】
1.如图,用5个小正方形和1个大正方形拼成一个更大的正方形,已知最大正方形的周长为120厘米,大正方形的面积是多少平方厘米
解析:
大正方形的边长是小正方形边长的2倍,每个小正方形的边长为
120÷4÷(1+2)=10(厘米),大正方形的边长为10×2=20(厘米),大正方形的面积是 20×20=400(平方厘米)。
2.如图,六个相同的长方形围成了大、小两个正方形,已知小正方形的面积是36平方厘米,则每个小长方形的面积是多少平方厘米
解析:
小正方形的面积为36平方厘米,边长为6厘米,小长方形的长就是6厘米,2个宽+1个长=2个长,所以小长方形的宽=6÷2=3(厘米),每个小长方形的面积为6×3=18(平方厘米)。
3. 5个相同的长方形放在一个正方形内,所有长方形的边都平行于正方形的对应边,正方形的边长为24厘米,每个小长方形的面积是多少
解析:
从水平方向观察,通过平移,不难发现3个长方形的长=24厘米,则长为24÷3=8(厘米);从竖直方向观察,2条长+2条宽=24厘米,则宽为24÷2—8= 4(厘米),那么每个小长方形的面积为8×4=32(平方厘米)。
【奥数拓展四】割补、平移或旋转法求图形的面积(二)。
1. 下图中所标的数为相应区域的面积,求阴影部分的面积。
解析:
因为面积为9与面积为3的两个长方形的长相等,所以,面积为9的长方形宽是面积为3的长方形宽的9÷3=3倍,那么阴影部分的面积为7×3=21
2. 一张长方形纸片,在长边上剪下10厘米、宽边上剪下5厘米,余下的部分正 好是一个正方形,已知正方形面积比原长方形纸片面积少140平方厘米,求原长方形纸片的面积。
解析:
已知正方形面积比原长方形纸片面积少140平方厘米,从图中可以看出是长方形A、B、C的面积之和,由于余下的部分是一个正方形,所以长方形C的宽与长方形A的长相等,因此可以先算正方形边长,正方形边长=(140— 10×5)÷(5+10)=6(厘米),那么原长方形纸片面积为140+ 6×6=176(平方厘米)
【专项训练】
1.计算长方形A、B、C、D的面积之和。(单位:平方厘米)
解析:
C的面积为20×24÷30=16(平方厘米);
A的面积为20×8÷16=10(平方厘米);
B的面积为6×16÷8=12(平方厘米);
D的面积为24×12÷16=18(平方厘米),A+B+C+D=10+12+16+18=56(平方厘米)。
2.如图所示,在大长方形中放入六个形状大小相同的长方形,图中阴影部分的面积是多少
解析:
设小长方形的长边为a,短边为b,从水平方向观察可知:a+36=14;从垂直方向观察可知:2b+6=a+ b,即a =b+6,将a=b+6代入a+3b=14中,可得
b=(14—6)÷(3+1)=2,a=2+6=8,大长方形的长为14,宽为6+2×2=10,阴影部分面积为14×10—8×2×6=44
3.长方形ABCD的周长是14厘米,在它的每条边上各画一个以该边为边长的正 方形(如图),已知这四个正方形的面积和是50平方厘米,那么长方形ABCD的面积是多少平方厘米
解析:
如图所示,将长方形DFGH补在原图右上角,得到正方形BEGI,它的边长等于14÷2=7(厘米),又因为正方形ADHI与CEFD的面积和为50÷2= 25(平方厘米),所以长方形ABCD的面积为:(7×7—25)÷2=12(平方厘米)
21世纪教育网(www.21cnjy.com)
