2024-2025学年广西南宁市南宁三中五象校区高二(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年广西南宁市南宁三中五象校区高二(上)开学数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 100.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-20 16:01:27 | ||
图片预览



文档简介
2024-2025学年广西南宁三中五象校区高二(上)开学数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.复数的虚部为( )
A. B. C. D.
2.如图,已知等腰直角三角形,是由斜二测画法得到的一个水平放置的平面图形的直观图,斜边,则这个平面图形的面积是( )
A.
B.
C.
D.
3.已知集合,,则是的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 既不充分又不必要条件 D. 充要条件
4.已知向量与能作为平面向量的一组基底,若与共线,则的值是( )
A. B. C. D.
5.如图为某地年至年的粮食年产量折线图,则下列说法错误的是( )
A. 这年粮食年产量的极差为
B. 这年粮食年产量的第百分位数为
C. 这年粮食年产量的平均数为
D. 前年的粮食年产量的方差小于后年粮食年产量的方差
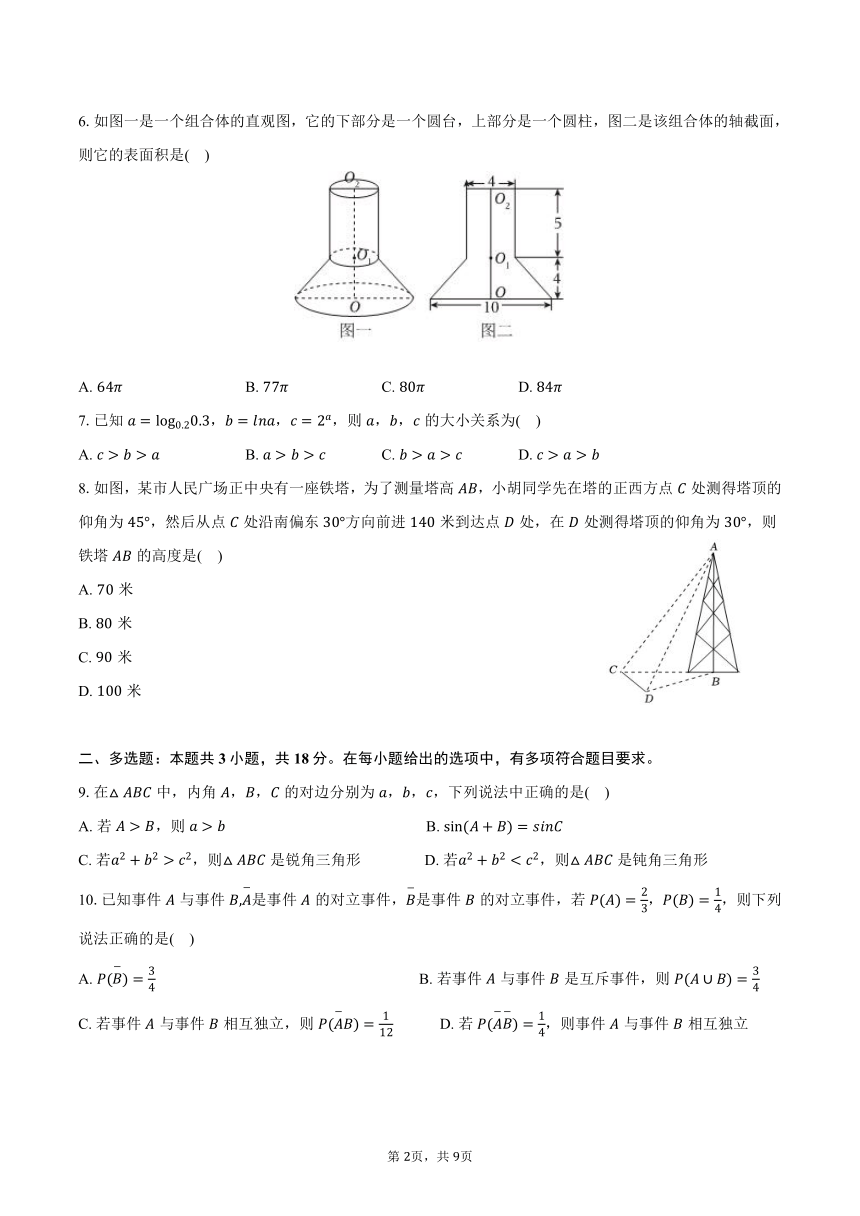
6.如图一是一个组合体的直观图,它的下部分是一个圆台,上部分是一个圆柱,图二是该组合体的轴截面,则它的表面积是( )
A. B. C. D.
7.已知,,,则,,的大小关系为( )
A. B. C. D.
8.如图,某市人民广场正中央有一座铁塔,为了测量塔高,小胡同学先在塔的正西方点处测得塔顶的仰角为,然后从点处沿南偏东方向前进米到达点处,在处测得塔顶的仰角为,则铁塔的高度是( )
A. 米
B. 米
C. 米
D. 米
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.在中,内角,,的对边分别为,,,下列说法中正确的是( )
A. 若,则 B.
C. 若,则是锐角三角形 D. 若,则是钝角三角形
10.已知事件与事件是事件的对立事件,是事件的对立事件,若,,则下列说法正确的是( )
A. B. 若事件与事件是互斥事件,则
C. 若事件与事件相互独立,则 D. 若,则事件与事件相互独立
11.如图所示,棱长为的正方体中,为线段上的动点不含端点,则下列结论正确的是( )
A.
B. 与所成的角可能是
C. 是定值
D. 当时,点到平面的距离为
三、填空题:本题共3小题,每小题5分,共15分。
12.若,且为锐角,则实数的取值范围是______.
13.已知角的终边在第一象限,,则 ______.
14.如图,三棱锥的四个顶点都在球的球面上,,是边长为的正三角形,二面角的大小为,则球的体积为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,,且.
求向量与的夹角;
求的值.
16.本小题分
如图,在四棱锥中,平面,点是的中点.
若底面是平行四边形,求证:平面;
若底面是菱形,证明:.
17.本小题分
近年来,“直播带货”受到越来越多人的喜爱,目前已经成为推动消费的一种流行营销形式某直播平台有个直播商家,对其进行调查统计,发现所售商品多为小吃、衣帽、生鲜、玩具、饰品类等,各类直播商家所占比例如图所示为了更好地服务买卖双方,该直播平台打算用分层抽样的方式抽取个直播商家进行问询交流.
应抽取小吃类、生鲜类商家各多少家?
在问询了解直播商家的利润状况时,工作人员对抽取的个商家的平均日利润进行了统计单位:元,所得频率直方图如图所示.
估计该直播平台商家平均日利润的百分位数与平均数求平均数时同一组中的数据用该组区间中点的数值为代表;
若将平均日利润超过元的商家称为“优质商家”,估计该直播平台“优质商家”的个数.
18.本小题分
在中,角,,的对边分别为,,,已知.
求角的大小;
若,求的面积;
若为的中点,求的长.
19.本小题分
如图,四棱台中,上、下底面均是正方形,且侧面是全等的等腰梯形,,,分别为,的中点,上下底面中心的连线垂直于上下底面,且与侧棱所在直线所成的角为.
求证:平面;
求点到平面的距离;
边上是否存在点,使得直线与平面所成的角的正弦值为,若存在,求出线段的长;若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:已知向量,,且.
设向量与的夹角为,
因为,
所以,
即,
解得,
又,
所以,
即向量与的夹角为.
由知,
故.
16.证明:如图,连接交于点,连接,
因是平行四边形,则为的中点,
又因为的中点,故E,
又因为面,面,
所以平面;
因是菱形,则,
又平面,平面,则,
因,,平面,则平面,
又平面,
故BD.
17.解:根据分层抽样知:
应抽取小吃类家,生鲜类家,
所以应抽取小吃类家,生鲜类家;
根据题意可得,
解得,
设百分位数为,因为,
所以,
解得,
所以该直播平台商家平均日利润的百分位数为元,
平均数为,
所以该直播平台商家平均日利润的平均数为元;
,
所以估计该直播平台“优秀商家”的个数为.
18.解:,
,即,
由正弦定理得,由余弦定理得,
,
;
,
由余弦定理得,
,
;
为的中点,
在中,由余弦定理得,即,
又,得,
为的中点,
,两边平方得,
,即中线的长度为.
19.解:证明:由题设可得四棱台为正四棱台,故可建立如图所示空间直角坐标系:
,,分别为,的中点,上下底面中心的连线垂直于上下底面,且与侧棱所在直线所成的角为.
则,
所有,
设平面的一个法向量为,
则,即,
令,则,,所以,
因为,且平面,
所以平面;
易知,则,
所以点到平面的距离为;
假设在边上存在点,设,
则,
因为直线与平面所成的角的正弦值为,
所以,
即,解得或舍去,
则,此时.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.复数的虚部为( )
A. B. C. D.
2.如图,已知等腰直角三角形,是由斜二测画法得到的一个水平放置的平面图形的直观图,斜边,则这个平面图形的面积是( )
A.
B.
C.
D.
3.已知集合,,则是的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 既不充分又不必要条件 D. 充要条件
4.已知向量与能作为平面向量的一组基底,若与共线,则的值是( )
A. B. C. D.
5.如图为某地年至年的粮食年产量折线图,则下列说法错误的是( )
A. 这年粮食年产量的极差为
B. 这年粮食年产量的第百分位数为
C. 这年粮食年产量的平均数为
D. 前年的粮食年产量的方差小于后年粮食年产量的方差
6.如图一是一个组合体的直观图,它的下部分是一个圆台,上部分是一个圆柱,图二是该组合体的轴截面,则它的表面积是( )
A. B. C. D.
7.已知,,,则,,的大小关系为( )
A. B. C. D.
8.如图,某市人民广场正中央有一座铁塔,为了测量塔高,小胡同学先在塔的正西方点处测得塔顶的仰角为,然后从点处沿南偏东方向前进米到达点处,在处测得塔顶的仰角为,则铁塔的高度是( )
A. 米
B. 米
C. 米
D. 米
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.在中,内角,,的对边分别为,,,下列说法中正确的是( )
A. 若,则 B.
C. 若,则是锐角三角形 D. 若,则是钝角三角形
10.已知事件与事件是事件的对立事件,是事件的对立事件,若,,则下列说法正确的是( )
A. B. 若事件与事件是互斥事件,则
C. 若事件与事件相互独立,则 D. 若,则事件与事件相互独立
11.如图所示,棱长为的正方体中,为线段上的动点不含端点,则下列结论正确的是( )
A.
B. 与所成的角可能是
C. 是定值
D. 当时,点到平面的距离为
三、填空题:本题共3小题,每小题5分,共15分。
12.若,且为锐角,则实数的取值范围是______.
13.已知角的终边在第一象限,,则 ______.
14.如图,三棱锥的四个顶点都在球的球面上,,是边长为的正三角形,二面角的大小为,则球的体积为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知向量,,且.
求向量与的夹角;
求的值.
16.本小题分
如图,在四棱锥中,平面,点是的中点.
若底面是平行四边形,求证:平面;
若底面是菱形,证明:.
17.本小题分
近年来,“直播带货”受到越来越多人的喜爱,目前已经成为推动消费的一种流行营销形式某直播平台有个直播商家,对其进行调查统计,发现所售商品多为小吃、衣帽、生鲜、玩具、饰品类等,各类直播商家所占比例如图所示为了更好地服务买卖双方,该直播平台打算用分层抽样的方式抽取个直播商家进行问询交流.
应抽取小吃类、生鲜类商家各多少家?
在问询了解直播商家的利润状况时,工作人员对抽取的个商家的平均日利润进行了统计单位:元,所得频率直方图如图所示.
估计该直播平台商家平均日利润的百分位数与平均数求平均数时同一组中的数据用该组区间中点的数值为代表;
若将平均日利润超过元的商家称为“优质商家”,估计该直播平台“优质商家”的个数.
18.本小题分
在中,角,,的对边分别为,,,已知.
求角的大小;
若,求的面积;
若为的中点,求的长.
19.本小题分
如图,四棱台中,上、下底面均是正方形,且侧面是全等的等腰梯形,,,分别为,的中点,上下底面中心的连线垂直于上下底面,且与侧棱所在直线所成的角为.
求证:平面;
求点到平面的距离;
边上是否存在点,使得直线与平面所成的角的正弦值为,若存在,求出线段的长;若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:已知向量,,且.
设向量与的夹角为,
因为,
所以,
即,
解得,
又,
所以,
即向量与的夹角为.
由知,
故.
16.证明:如图,连接交于点,连接,
因是平行四边形,则为的中点,
又因为的中点,故E,
又因为面,面,
所以平面;
因是菱形,则,
又平面,平面,则,
因,,平面,则平面,
又平面,
故BD.
17.解:根据分层抽样知:
应抽取小吃类家,生鲜类家,
所以应抽取小吃类家,生鲜类家;
根据题意可得,
解得,
设百分位数为,因为,
所以,
解得,
所以该直播平台商家平均日利润的百分位数为元,
平均数为,
所以该直播平台商家平均日利润的平均数为元;
,
所以估计该直播平台“优秀商家”的个数为.
18.解:,
,即,
由正弦定理得,由余弦定理得,
,
;
,
由余弦定理得,
,
;
为的中点,
在中,由余弦定理得,即,
又,得,
为的中点,
,两边平方得,
,即中线的长度为.
19.解:证明:由题设可得四棱台为正四棱台,故可建立如图所示空间直角坐标系:
,,分别为,的中点,上下底面中心的连线垂直于上下底面,且与侧棱所在直线所成的角为.
则,
所有,
设平面的一个法向量为,
则,即,
令,则,,所以,
因为,且平面,
所以平面;
易知,则,
所以点到平面的距离为;
假设在边上存在点,设,
则,
因为直线与平面所成的角的正弦值为,
所以,
即,解得或舍去,
则,此时.
第1页,共1页
同课章节目录
