24.3.1 相似三角形 课件
图片预览



文档简介
课件25张PPT。相似三角形
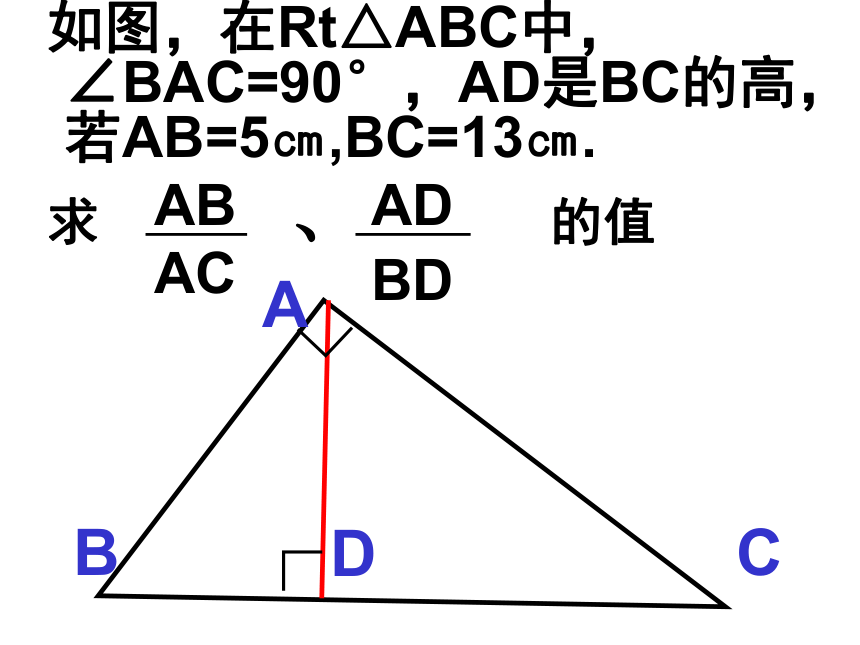
冯家中学 如图,在Rt△ABC中,∠BAC=90°,AD是BC的高,若AB=5㎝,BC=13㎝.
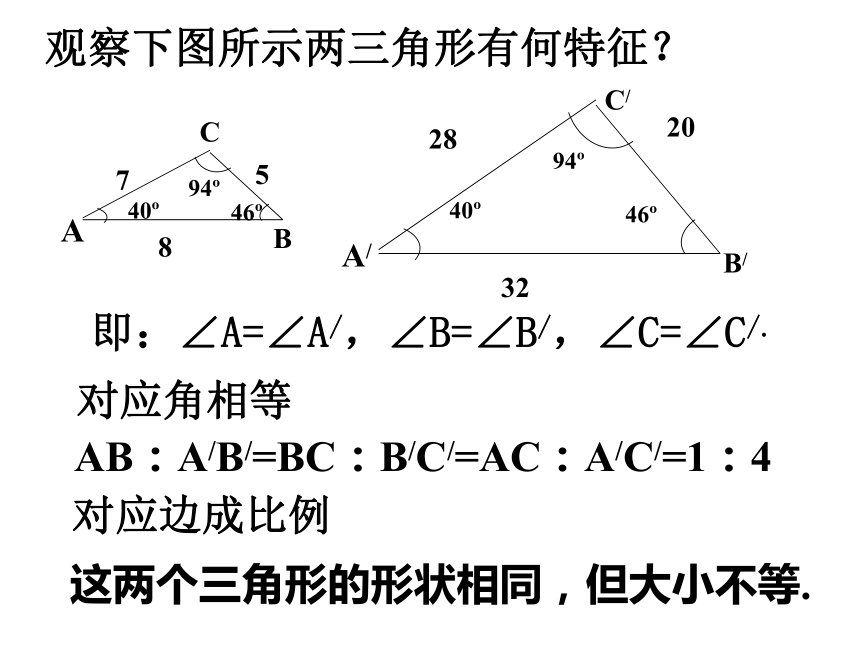
求 、 的值ABACADBD观察下图所示两三角形有何特征?A/AB/BC/C即:∠A=∠A/,∠B=∠B/,∠C=∠C/.AB:A/B/=BC:B/C/=AC:A/C/=1:4对应角相等对应边成比例这两个三角形的形状相同,但大小不等.
对应角相等、对应边成比例的两个三角形叫做相似三角形.?ABC与?DEF相似,记作:
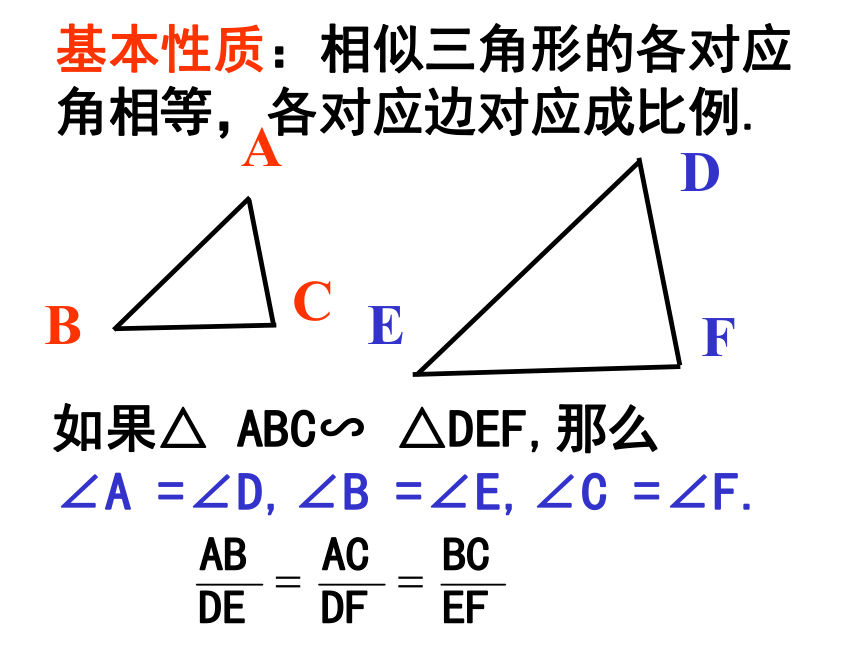
?ABC ∽?DEF相似三角形基本性质:相似三角形的各对应角相等,各对应边对应成比例.如果△ ABC∽ △DEF,那么
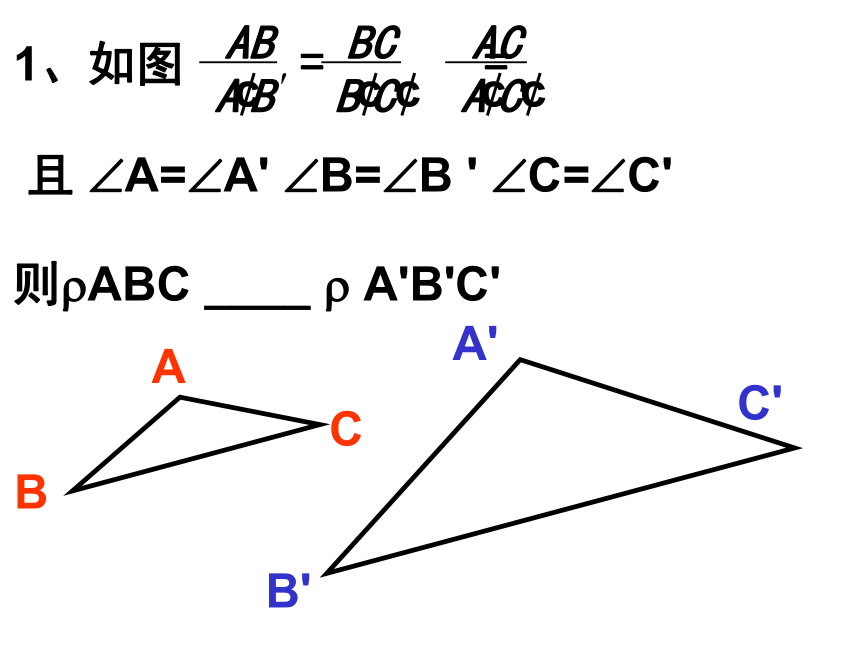
∠A =∠D,∠B =∠E,∠C =∠F. 如果?ABC∽?DEF,那么哪些角是对应角?哪些边是对应边?对应角有什么关系 ?对应边呢?什么是相似比? 相似三角形对应角相等,对应边成比例。对应边的比为相似比。 想一想1、如图
且 ?A=?A' ?B=?B ' ?C=?C'
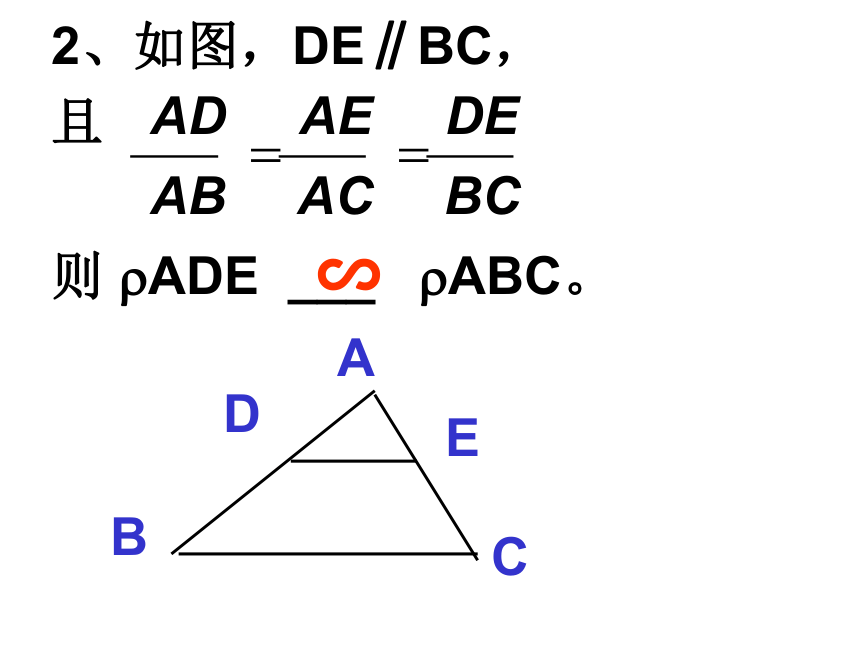
则?ABC ____ ? A'B'C' 2、如图,DE∥BC,
且
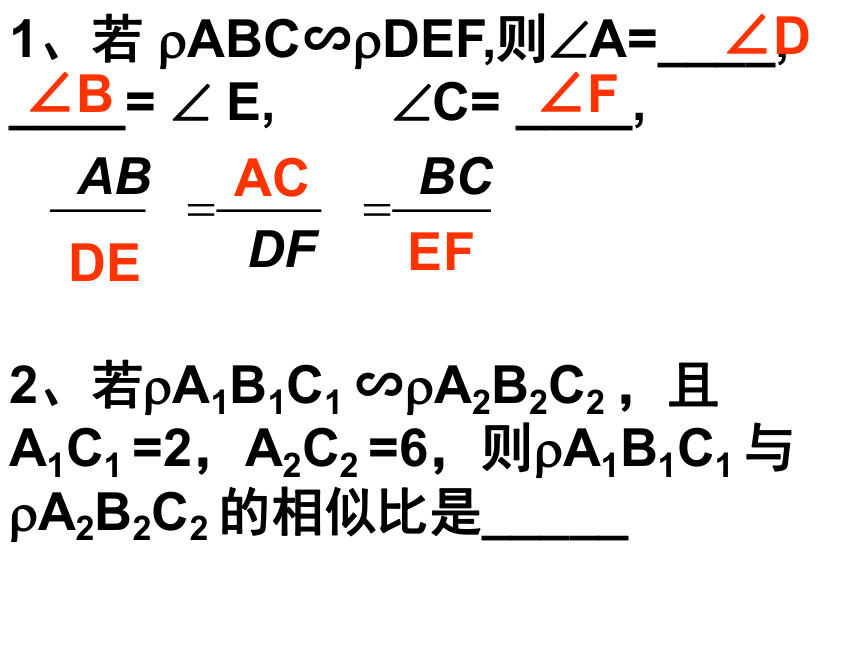
则 ?ADE ___ ?ABC。∽1、若 ?ABC∽?DEF,则?A=____, ____= ? E, ?C= ____,
2、若?A1B1C1 ∽?A2B2C2 ,且A1C1 =2,A2C2 =6,则?A1B1C1 与?A2B2C2 的相似比是_____∠D∠B∠FDEACEF例1、如图,有一块呈三角形形状的草坪,其中一边的长是20m,在这个草坪的图纸上,这条边长5cm,其他两边的长度都是3.5cm。求该草坪其他两边的实际长度。例2、如图,已知
DE ∥ BC,AE=50cm,EC=30cm,
BC=70cm,∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;
(2)求DE的长.
想一想:
在例2的条件下图中有哪些线段成比例?图中有互相平行的线段吗? 如图,分别根据下列已知条件和刚学得知识,试写出你能得出的结论。(1) DE ∥ BC;(1)(2)DE ∥AB;
(3)△ABC∽△ADE,其中∠ADE = ∠C(2)(3)1、有 一块三角形形状的土地 ,其中最长一边长20m ,在这块土地的 图纸上,这三边分别长5cm,2cm,4cm,则该土地其他两边的实际长度 分别为______、______。
2、已知?ABC ∽?A'B'C' ,若? ABC三边长分别为3,4,5,则?A'B'C' 的形状 是__________,若 ?A'B'C'的最长边为15,则 S ? A'B'C' = _____.8m16m直角三角形541、已知:如图AB是斜靠的长梯,
梯脚B距墙根C1?6米,梯上点D距离
墙1?4米,已知BD=0.5米,且
ADE∽ ?ABC,那么
AD=_____米,梯子的长度
为______米。43.52、如图,已知?ADE∽?ABC,
AB=10,AD=6,BC=12,?A=56°,?ADE=40°,则?ACB=____度,DE=_____。
547.2例3:如图,在△ABC中,DE∥BC,D,E分别在AB,AC上.求证:△ADE∽△ABC.F证明:在△ADE和△ABC中,∠A=∠A,∵DE∥BC∴∠ADE=∠B∠AED=∠C,过点E作EF∥AB,交BC于F,
则四边形BFED是平行四边形.∴DE=BF.又∵EF∥AB,∴∴∴△ADE∽△ABC.练习:如图D为△ABC的边AC上一点,过点D作DE∥AB,交BC于E.已知BE:EC=1:2,AB=6,求DE的长.相似比k(对应边的比值)课堂小结对应角相等对应边成比例定义表示法“ ∽”相似三角形相似三角形判定预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似. 1、若?ABC∽ ? A ' B 'C ',相似比为k (k?1),则k的值应是( )(A)?A: ? A' (B)BC : B ' C '
(C) ? A ' : ? A (D)A ' B ' : AB
2.若两个相似三角形的相似比为1,则这两个三角形必________.
3、已知?ABC∽ ? A ' B ' C ',如果?A=55° ,? B=100°,则
?C'=_______.B全等25° 4、已知?ABC∽ ? A ' B ' C '且相似比k= ,若AB=10,
则A' B ' =______.
5 、已知?A1B1C1 与?A2B2C2 的相似比是k,则?A2B2C2与?A1B1C1 的相似比是________.
207.?ABC的三边长分别为 、 、2,? A′B′C′的两边长为 1和 ,若?ABC ∽? A′B′C′ ,则? A′B′C′ 的第三边长应为_____。6、如图,? ABO ∽? CDO则AB与CD的位置关系是________。AB ∥ CD ?ABC ∽?DEF若?ABC的三边长分别为5cm、6cm、7cm、而4cm是?DEF中一边的长度,你能求出?DEF的另外两边的长度吗?试说明理由。已知a、b、c是△ABC的三边, 且
= =
a+b+c=12,试判断的形状a+43b+34c+82黄金分割: 古希腊数学家欧多克索斯发现:将一条线段(AB)分割成大小两条线段(AP、BP)。若小段与大段的长度之比等于大段的长度与全长之比。即APB
冯家中学 如图,在Rt△ABC中,∠BAC=90°,AD是BC的高,若AB=5㎝,BC=13㎝.
求 、 的值ABACADBD观察下图所示两三角形有何特征?A/AB/BC/C即:∠A=∠A/,∠B=∠B/,∠C=∠C/.AB:A/B/=BC:B/C/=AC:A/C/=1:4对应角相等对应边成比例这两个三角形的形状相同,但大小不等.
对应角相等、对应边成比例的两个三角形叫做相似三角形.?ABC与?DEF相似,记作:
?ABC ∽?DEF相似三角形基本性质:相似三角形的各对应角相等,各对应边对应成比例.如果△ ABC∽ △DEF,那么
∠A =∠D,∠B =∠E,∠C =∠F. 如果?ABC∽?DEF,那么哪些角是对应角?哪些边是对应边?对应角有什么关系 ?对应边呢?什么是相似比? 相似三角形对应角相等,对应边成比例。对应边的比为相似比。 想一想1、如图
且 ?A=?A' ?B=?B ' ?C=?C'
则?ABC ____ ? A'B'C' 2、如图,DE∥BC,
且
则 ?ADE ___ ?ABC。∽1、若 ?ABC∽?DEF,则?A=____, ____= ? E, ?C= ____,
2、若?A1B1C1 ∽?A2B2C2 ,且A1C1 =2,A2C2 =6,则?A1B1C1 与?A2B2C2 的相似比是_____∠D∠B∠FDEACEF例1、如图,有一块呈三角形形状的草坪,其中一边的长是20m,在这个草坪的图纸上,这条边长5cm,其他两边的长度都是3.5cm。求该草坪其他两边的实际长度。例2、如图,已知
DE ∥ BC,AE=50cm,EC=30cm,
BC=70cm,∠BAC=450,∠ACB=400.
(1)求∠AED和∠ADE的大小;
(2)求DE的长.
想一想:
在例2的条件下图中有哪些线段成比例?图中有互相平行的线段吗? 如图,分别根据下列已知条件和刚学得知识,试写出你能得出的结论。(1) DE ∥ BC;(1)(2)DE ∥AB;
(3)△ABC∽△ADE,其中∠ADE = ∠C(2)(3)1、有 一块三角形形状的土地 ,其中最长一边长20m ,在这块土地的 图纸上,这三边分别长5cm,2cm,4cm,则该土地其他两边的实际长度 分别为______、______。
2、已知?ABC ∽?A'B'C' ,若? ABC三边长分别为3,4,5,则?A'B'C' 的形状 是__________,若 ?A'B'C'的最长边为15,则 S ? A'B'C' = _____.8m16m直角三角形541、已知:如图AB是斜靠的长梯,
梯脚B距墙根C1?6米,梯上点D距离
墙1?4米,已知BD=0.5米,且
ADE∽ ?ABC,那么
AD=_____米,梯子的长度
为______米。43.52、如图,已知?ADE∽?ABC,
AB=10,AD=6,BC=12,?A=56°,?ADE=40°,则?ACB=____度,DE=_____。
547.2例3:如图,在△ABC中,DE∥BC,D,E分别在AB,AC上.求证:△ADE∽△ABC.F证明:在△ADE和△ABC中,∠A=∠A,∵DE∥BC∴∠ADE=∠B∠AED=∠C,过点E作EF∥AB,交BC于F,
则四边形BFED是平行四边形.∴DE=BF.又∵EF∥AB,∴∴∴△ADE∽△ABC.练习:如图D为△ABC的边AC上一点,过点D作DE∥AB,交BC于E.已知BE:EC=1:2,AB=6,求DE的长.相似比k(对应边的比值)课堂小结对应角相等对应边成比例定义表示法“ ∽”相似三角形相似三角形判定预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似. 1、若?ABC∽ ? A ' B 'C ',相似比为k (k?1),则k的值应是( )(A)?A: ? A' (B)BC : B ' C '
(C) ? A ' : ? A (D)A ' B ' : AB
2.若两个相似三角形的相似比为1,则这两个三角形必________.
3、已知?ABC∽ ? A ' B ' C ',如果?A=55° ,? B=100°,则
?C'=_______.B全等25° 4、已知?ABC∽ ? A ' B ' C '且相似比k= ,若AB=10,
则A' B ' =______.
5 、已知?A1B1C1 与?A2B2C2 的相似比是k,则?A2B2C2与?A1B1C1 的相似比是________.
207.?ABC的三边长分别为 、 、2,? A′B′C′的两边长为 1和 ,若?ABC ∽? A′B′C′ ,则? A′B′C′ 的第三边长应为_____。6、如图,? ABO ∽? CDO则AB与CD的位置关系是________。AB ∥ CD ?ABC ∽?DEF若?ABC的三边长分别为5cm、6cm、7cm、而4cm是?DEF中一边的长度,你能求出?DEF的另外两边的长度吗?试说明理由。已知a、b、c是△ABC的三边, 且
= =
a+b+c=12,试判断的形状a+43b+34c+82黄金分割: 古希腊数学家欧多克索斯发现:将一条线段(AB)分割成大小两条线段(AP、BP)。若小段与大段的长度之比等于大段的长度与全长之比。即APB
