24.3.2 相似三角形的判定(1) 课件
文档属性
| 名称 | 24.3.2 相似三角形的判定(1) 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 653.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-12 00:00:00 | ||
图片预览


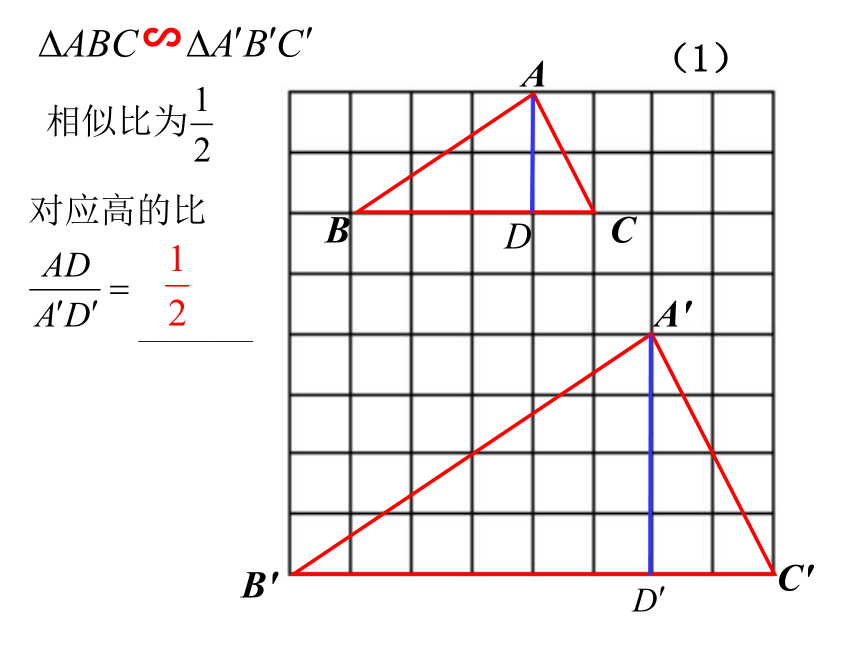
文档简介
课件27张PPT。课前复习:(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)如何判定两个三角形相似?①两个角对应相等;
②两边对应成比例,且夹角相等;
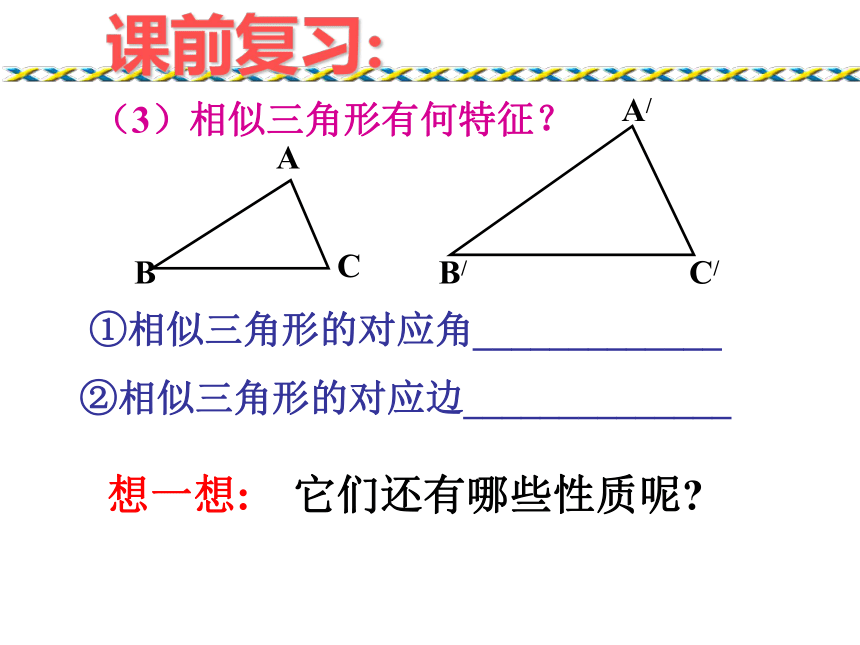
③三边对应成比例.ABCA/B/C/ ①相似三角形的对应角_____________
②相似三角形的对应边______________想一想: 它们还有哪些性质呢?课前复习:(3)相似三角形有何特征?一个三角形有三条重要线段:
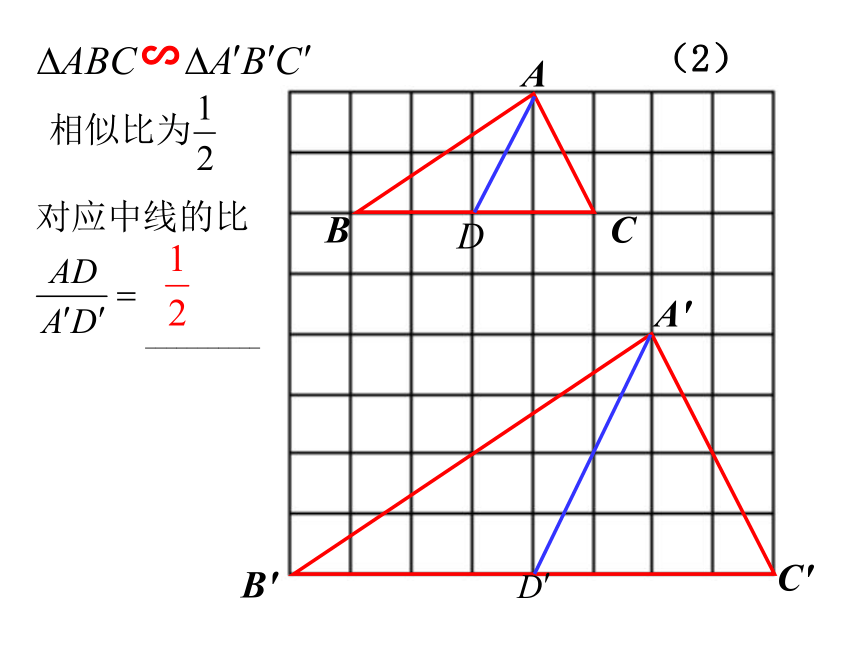
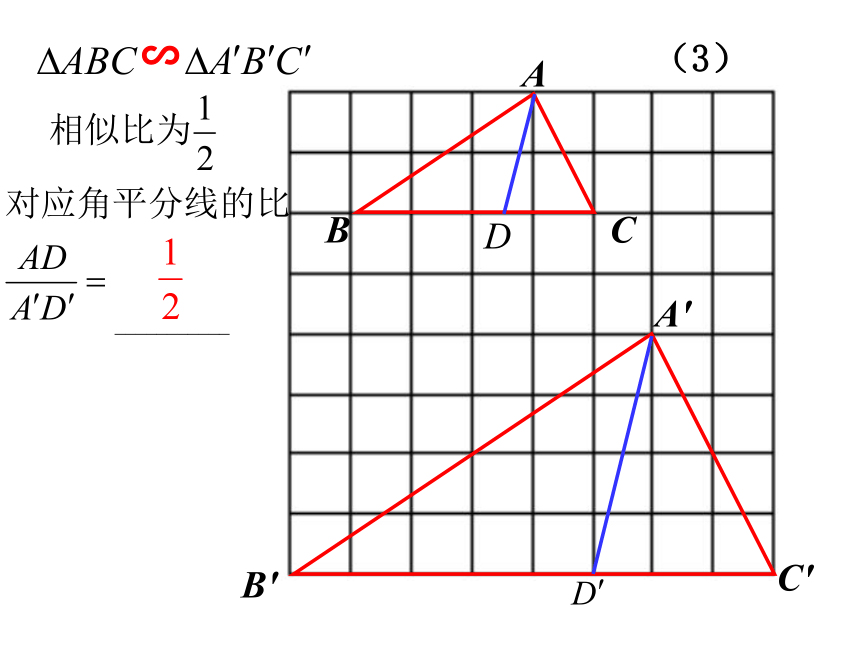
________________如果两个三角形相似,
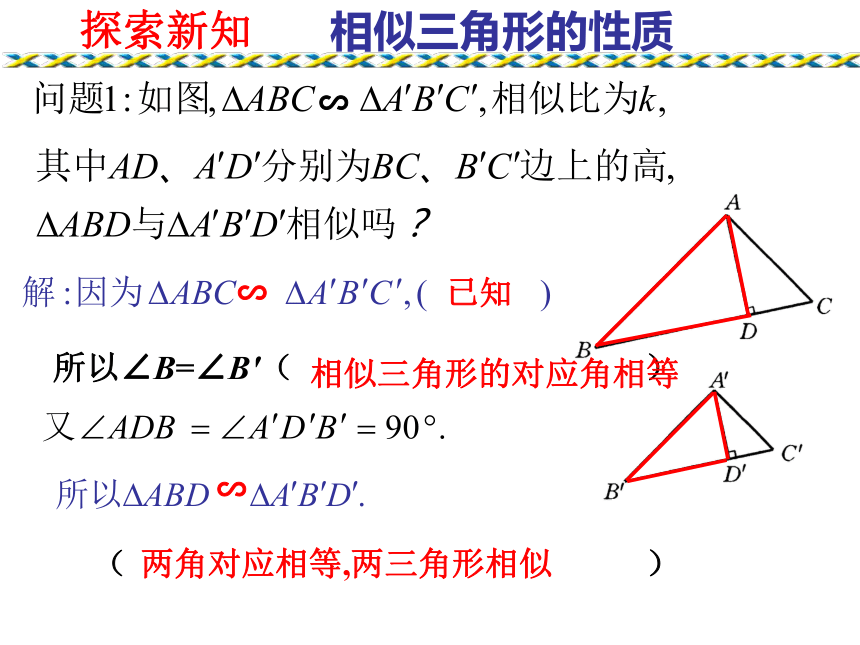
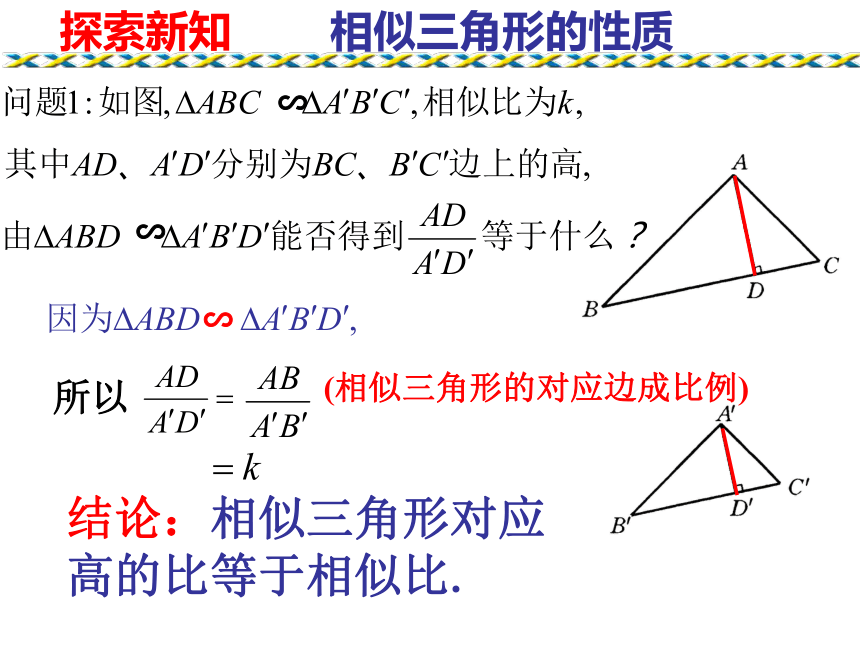
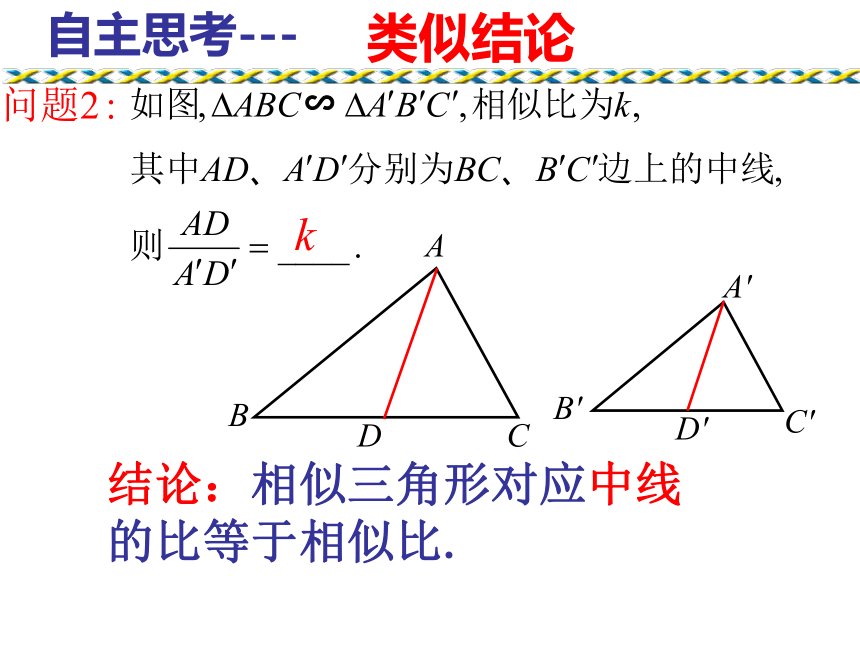
那么这些对应线段有什么关系呢?情境引入高、中线、角平分线∽(1)∽(2)∽(3)探索新知两角对应相等,两三角形相似∽∽已知所以∠B=∠B′( )相似三角形的对应角相等 ∽( )相似三角形的性质探索新知∽所以(相似三角形的对应边成比例)∽∽相似三角形的性质结论:相似三角形对应高的比等于相似比.类似结论D'C'B'A'DCBA∽自主思考---结论:相似三角形对应中线的比等于相似比.A′C′B′CBAE′E∽类似结论自主思考---结论:相似三角形对应角的角平分线的比等于相似比.问题: 两个相似三角形的周长比
会等于相似比吗?相似三角形的性质图24.3.10中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,它们都相似.(2)与(1)的相似比=__________,
(2)与(1)的面积比=__________;
(3)与(1)的相似比=__________,
(3)与(1)的面积比=__________.2:14:13:19:1 面积比和相似比之间有什么联系呢?猜想已知:△ABC∽△A′B′C′,且相似比为k,AD、 A′D′分别是△ABC、 △A′B′C′对应边
BC、 B′C′上的高,求证:证明 ∵ △ABC∽△A′B′C′, ∴ ,,∴ 证明已知两个三角形相似,请完成下列表格: 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结相似比的平方相似三角形的性质相似多边形也有同样的结论1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.2.相似三角形对应边的比为0.4,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.3∶5 0.4当堂训练0.40.40.16当堂训练3.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍。
4.两个相似三角形的一对对应边分别是35厘米和14 厘米,(1)它们的周长差60厘米,这两个三角形的周长分别是________________。(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。2510100cm、40cm50cm2、8cm25.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.2 : 1解:相似.因为相似比是
所以面积比是4 : 1当堂训练 (1)△ADE与△ABC相似吗?如果相似, 求它们的相似比. ABCDE1∶4 (2) △ADE的周长︰△ABC的周长=_______. 1∶4 例1、如图,DE∥BC, DE = 1, BC = 4,例题赏析1、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长︰△ABC的周长= 。 1:32.右图中,若D,E分别是AB,AC边上的中点,且DE=4则BC= ____83.右图中, DE∥BC,S△ADE:S四边形DBCE = 1:8,则AE:AC=_____1:3课堂训练:例2、如图,在 ABCD中,若E是AB的中点,
则(1)?AEF与?CDF的相似比为______.
(2)若?AEF的面积为5 cm2,
则?CDF的面积为______.BFEDCA例题赏析1 : 220 cm2变式练习:
1、如图是一个照相机成像的示意图。如果底片AB宽35mm,焦距是70mm,拍摄5m外的景物A′B ′有多宽?如果焦距是50mm呢?70mm5mABA′OB′大胆尝试4. 在△ABCAC=4,AB=5.D是AC上一动点,且∠ADE=∠B,设AD=x,AE=y,写出y与x之间的函数关系式.试确定x的取值范围.A解: ∵∠A=∠A ∵∠ADE=∠B ∴△ADE∽△ABC ( ) ∴AD:AB=AE:AC ∴x:5=y:4 ∴y=0.8x (0<x≤4)
BACO如图:
写出其中的几个等积式
①AC2=
②BC2=
③OC2=AO×ABBO×AB
AO×BO
若AC=3,AO=1.写出A.B.C三点的坐标.(-1,0)(8,0)(0,2 )②如果把正方形的零件改变为加工矩形零件,设DP=x,DE=y,写出y与x之间的函数关系式,试确定x的取值范围。 PBACDEFMN如图,△ABC是一 块余料,边AB=90厘米,高CN=60厘米,要把它加工成正方形零件,使正方形 的一边在AB上,其余两个顶点分别在BC、AC上 ①这个正方形零件的边长是多少?③当DE是DP的1.5倍时恰好符合要求,求此时零件的面积是多少? ④在问题3中,具体操作时,发现在AB线段上离B点34cm处有一蛀虫洞,请你确定一下,它是否影响余料的使用,说明理由。(量得BN=70cm)PBACDEFMNBACDEF图一图二课外拓展:
右图中,在一直角三角形余料中截出一个面积最大的正方形零件,应如何截取? (设正方形的三边分别是3、4、5、那么最大的面积是多少?) BAC解:设正方形DEFP的边长为x厘米。
因为DE∥AB,所以△CDE∽ △CBA
所以
问题解答:PBACDEFMN
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)如何判定两个三角形相似?①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.ABCA/B/C/ ①相似三角形的对应角_____________
②相似三角形的对应边______________想一想: 它们还有哪些性质呢?课前复习:(3)相似三角形有何特征?一个三角形有三条重要线段:
________________如果两个三角形相似,
那么这些对应线段有什么关系呢?情境引入高、中线、角平分线∽(1)∽(2)∽(3)探索新知两角对应相等,两三角形相似∽∽已知所以∠B=∠B′( )相似三角形的对应角相等 ∽( )相似三角形的性质探索新知∽所以(相似三角形的对应边成比例)∽∽相似三角形的性质结论:相似三角形对应高的比等于相似比.类似结论D'C'B'A'DCBA∽自主思考---结论:相似三角形对应中线的比等于相似比.A′C′B′CBAE′E∽类似结论自主思考---结论:相似三角形对应角的角平分线的比等于相似比.问题: 两个相似三角形的周长比
会等于相似比吗?相似三角形的性质图24.3.10中(1)、(2)、(3)分别是边长为1、2、3的等边三角形,它们都相似.(2)与(1)的相似比=__________,
(2)与(1)的面积比=__________;
(3)与(1)的相似比=__________,
(3)与(1)的面积比=__________.2:14:13:19:1 面积比和相似比之间有什么联系呢?猜想已知:△ABC∽△A′B′C′,且相似比为k,AD、 A′D′分别是△ABC、 △A′B′C′对应边
BC、 B′C′上的高,求证:证明 ∵ △ABC∽△A′B′C′, ∴ ,,∴ 证明已知两个三角形相似,请完成下列表格: 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
课堂小结相似比的平方相似三角形的性质相似多边形也有同样的结论1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.2.相似三角形对应边的比为0.4,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.3∶5 0.4当堂训练0.40.40.16当堂训练3.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的__________倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的__________倍。
4.两个相似三角形的一对对应边分别是35厘米和14 厘米,(1)它们的周长差60厘米,这两个三角形的周长分别是________________。(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是______________。2510100cm、40cm50cm2、8cm25.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.2 : 1解:相似.因为相似比是
所以面积比是4 : 1当堂训练 (1)△ADE与△ABC相似吗?如果相似, 求它们的相似比. ABCDE1∶4 (2) △ADE的周长︰△ABC的周长=_______. 1∶4 例1、如图,DE∥BC, DE = 1, BC = 4,例题赏析1、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长︰△ABC的周长= 。 1:32.右图中,若D,E分别是AB,AC边上的中点,且DE=4则BC= ____83.右图中, DE∥BC,S△ADE:S四边形DBCE = 1:8,则AE:AC=_____1:3课堂训练:例2、如图,在 ABCD中,若E是AB的中点,
则(1)?AEF与?CDF的相似比为______.
(2)若?AEF的面积为5 cm2,
则?CDF的面积为______.BFEDCA例题赏析1 : 220 cm2变式练习:
1、如图是一个照相机成像的示意图。如果底片AB宽35mm,焦距是70mm,拍摄5m外的景物A′B ′有多宽?如果焦距是50mm呢?70mm5mABA′OB′大胆尝试4. 在△ABCAC=4,AB=5.D是AC上一动点,且∠ADE=∠B,设AD=x,AE=y,写出y与x之间的函数关系式.试确定x的取值范围.A解: ∵∠A=∠A ∵∠ADE=∠B ∴△ADE∽△ABC ( ) ∴AD:AB=AE:AC ∴x:5=y:4 ∴y=0.8x (0<x≤4)
BACO如图:
写出其中的几个等积式
①AC2=
②BC2=
③OC2=AO×ABBO×AB
AO×BO
若AC=3,AO=1.写出A.B.C三点的坐标.(-1,0)(8,0)(0,2 )②如果把正方形的零件改变为加工矩形零件,设DP=x,DE=y,写出y与x之间的函数关系式,试确定x的取值范围。 PBACDEFMN如图,△ABC是一 块余料,边AB=90厘米,高CN=60厘米,要把它加工成正方形零件,使正方形 的一边在AB上,其余两个顶点分别在BC、AC上 ①这个正方形零件的边长是多少?③当DE是DP的1.5倍时恰好符合要求,求此时零件的面积是多少? ④在问题3中,具体操作时,发现在AB线段上离B点34cm处有一蛀虫洞,请你确定一下,它是否影响余料的使用,说明理由。(量得BN=70cm)PBACDEFMNBACDEF图一图二课外拓展:
右图中,在一直角三角形余料中截出一个面积最大的正方形零件,应如何截取? (设正方形的三边分别是3、4、5、那么最大的面积是多少?) BAC解:设正方形DEFP的边长为x厘米。
因为DE∥AB,所以△CDE∽ △CBA
所以
问题解答:PBACDEFMN
