华师大版九年级上册24.3.2 相似三角形的判定(3) 课件
文档属性
| 名称 | 华师大版九年级上册24.3.2 相似三角形的判定(3) 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 178.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-13 00:00:00 | ||
图片预览



文档简介
课件21张PPT。相似三角形的判定三黔江区冯家中学如何识别两三角形是否相似? ∵ DE∥BC
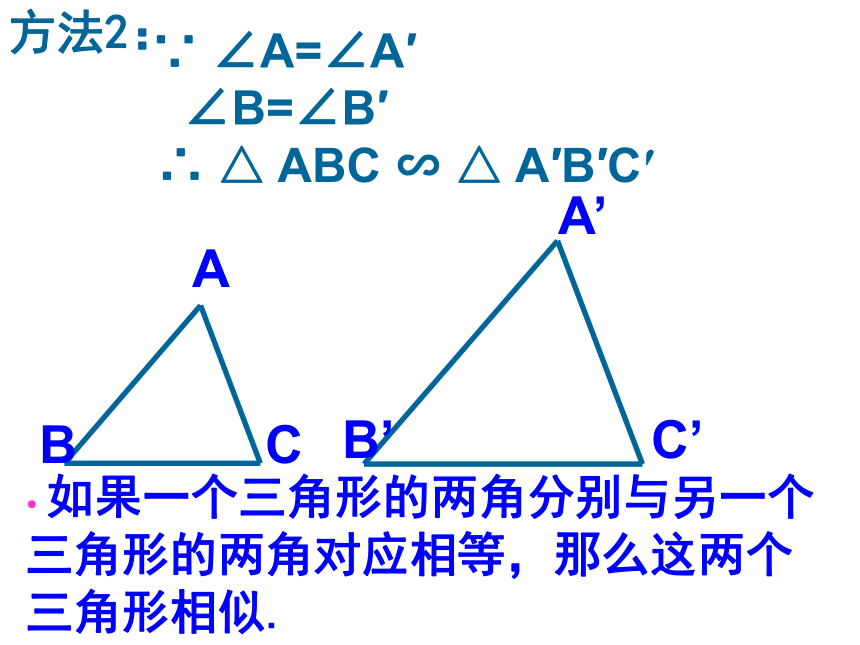
∴ △ ADE ∽ △ ABC 识别方法1:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。方法2: ∵ ∠A=∠A′
∠B=∠B′
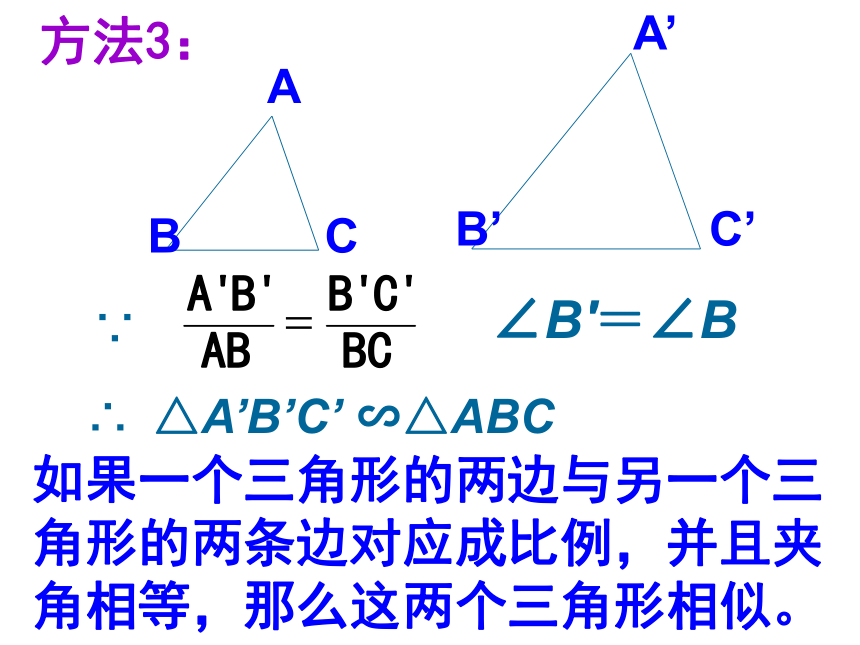
∴ △ ABC ∽ △ A′B′C′ 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.如果一个三角形的两边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。方法3:1,如图AB∥CD,则Δ___∽Δ___.
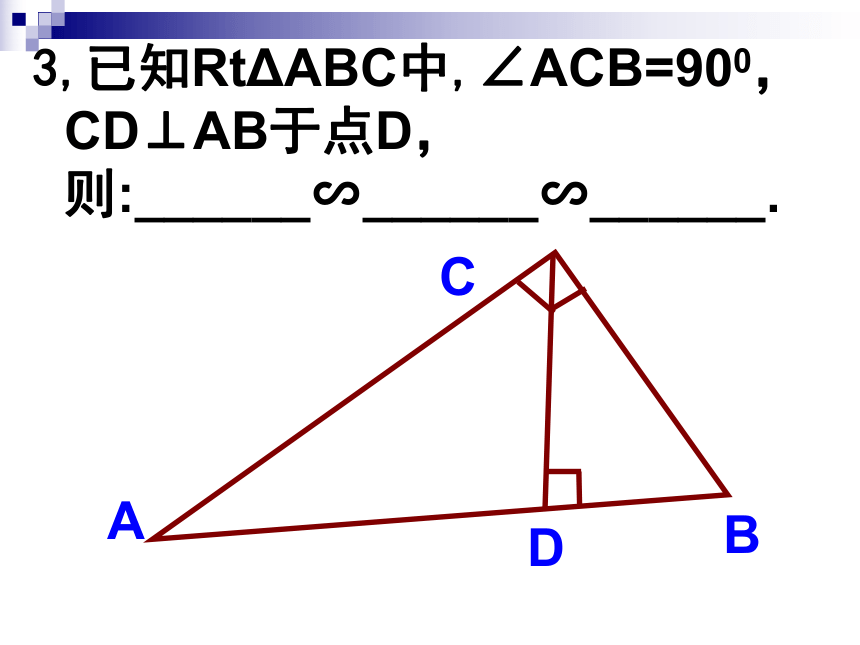
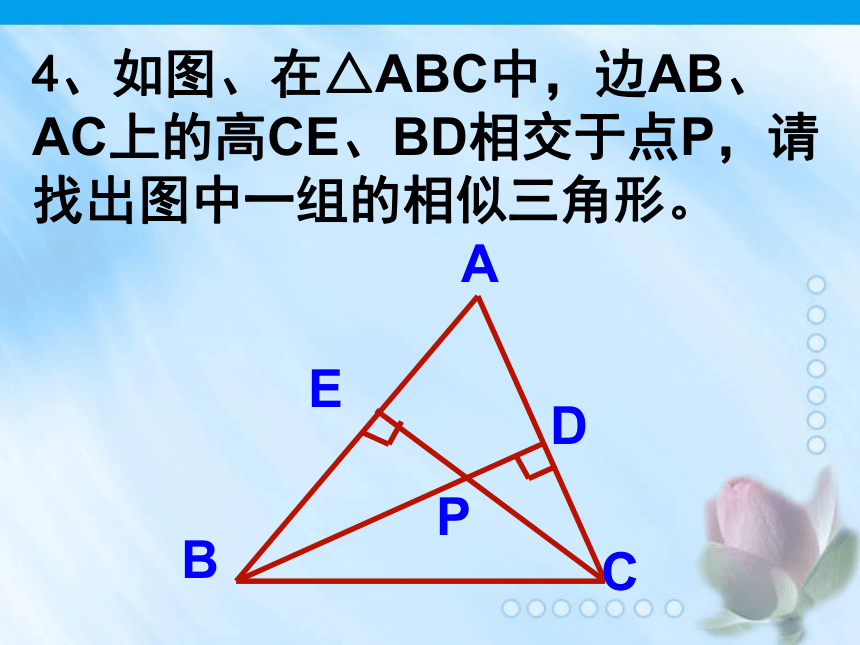
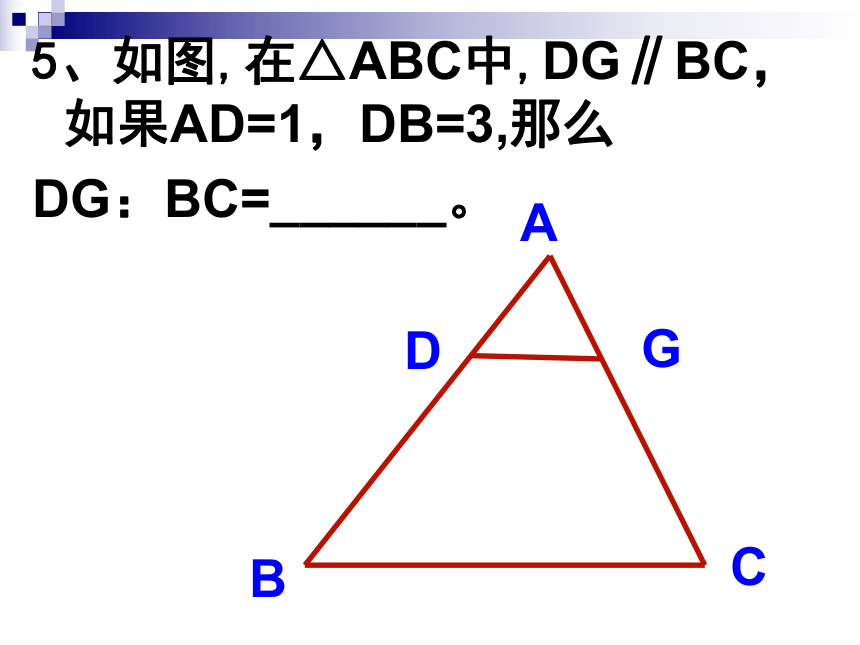
2.如果一个三角形的三边长分别为 2, 4 和5,与其相似三角形的最长边长为15,那么较大三角形的周长为________.3,已知RtΔABC中,∠ACB=900, CD⊥AB于点D,则:______∽______∽______.ABCD4、如图、在△ABC中,边AB、AC上的高CE、BD相交于点P,请找出图中一组的相似三角形。5、如图,在△ABC中,DG∥BC,如果AD=1,DB=3,那么
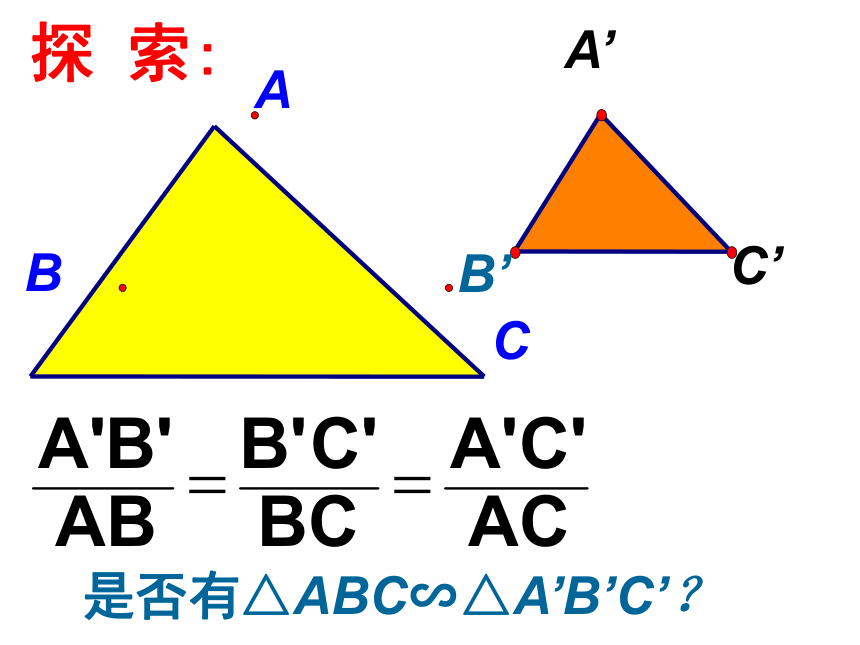
DG:BC=______。 是否有△ABC∽△A’B’C’?ABC探 索:ABC三边对应成 比例△ABC∽△A’B’C’结论:
如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似例:在△ABC和△A′B′C′中,已知:AB= 6cm, BC = 8 cm, AC = 10cm,A′B′= 18 cm, B′C′= 24cm, A′C′= 30cm试判定△ABC与△ A′B′C′是否相似,并说明理由. 两个等边三角形一定相似吗?△ABC与△A’B’C’都是等边三角形是否有 △ABC∽△A’B’C’问题:判定△ABC和△A′B′C′是否相似,并说明理由 。AB=12cm,BC=15cm,AC=24cm
A’B’=16cm,B’C’=20cm,A’C’=32cm 已知△ABC和 △A’B’C’,根据下列条件判断它们是否相似.(1)∠B=∠B’=75°, ∠C=50°, ∠A’=55°(2)∠A=45°, AB=12 , AC=15
∠A’=45°, A’B’=16 , A’C’=20(3) AB=12,BC=15,AC=24
A’B’=16, B’C’=20,A’C’=30试说明∠BAD=∠CAE.∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE如图,AB:AD=BC:DE=AC:AE,求证:∠ABD=∠ACEABCDE 已知△ABC 中∠C=90°,
D、E分别是AB、AC上的点且AD·AB= AE·AC
试说明:ED⊥AB如图,已知BD、CE为△ABC的高,试说明:∠ADE=∠ABC. 要做两个形状相同的三角形框架,其中一个三角形框架的三边的长分别为4、5、6,另一个三角形框架的一边长为2,请你想一想应该怎样选择材料可使这两个三角形相似? 你选的材料唯一吗?小结两个三角形相似的判定方法:(1)两角对应相等的 两个三角形相似.
(2)三边对应成比例的 两个三角形相似.
(3) 两边对应成比例且夹角相等的两个三角形相似.
∴ △ ADE ∽ △ ABC 识别方法1:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。方法2: ∵ ∠A=∠A′
∠B=∠B′
∴ △ ABC ∽ △ A′B′C′ 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.如果一个三角形的两边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。方法3:1,如图AB∥CD,则Δ___∽Δ___.
2.如果一个三角形的三边长分别为 2, 4 和5,与其相似三角形的最长边长为15,那么较大三角形的周长为________.3,已知RtΔABC中,∠ACB=900, CD⊥AB于点D,则:______∽______∽______.ABCD4、如图、在△ABC中,边AB、AC上的高CE、BD相交于点P,请找出图中一组的相似三角形。5、如图,在△ABC中,DG∥BC,如果AD=1,DB=3,那么
DG:BC=______。 是否有△ABC∽△A’B’C’?ABC探 索:ABC三边对应成 比例△ABC∽△A’B’C’结论:
如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似例:在△ABC和△A′B′C′中,已知:AB= 6cm, BC = 8 cm, AC = 10cm,A′B′= 18 cm, B′C′= 24cm, A′C′= 30cm试判定△ABC与△ A′B′C′是否相似,并说明理由. 两个等边三角形一定相似吗?△ABC与△A’B’C’都是等边三角形是否有 △ABC∽△A’B’C’问题:判定△ABC和△A′B′C′是否相似,并说明理由 。AB=12cm,BC=15cm,AC=24cm
A’B’=16cm,B’C’=20cm,A’C’=32cm 已知△ABC和 △A’B’C’,根据下列条件判断它们是否相似.(1)∠B=∠B’=75°, ∠C=50°, ∠A’=55°(2)∠A=45°, AB=12 , AC=15
∠A’=45°, A’B’=16 , A’C’=20(3) AB=12,BC=15,AC=24
A’B’=16, B’C’=20,A’C’=30试说明∠BAD=∠CAE.∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE如图,AB:AD=BC:DE=AC:AE,求证:∠ABD=∠ACEABCDE 已知△ABC 中∠C=90°,
D、E分别是AB、AC上的点且AD·AB= AE·AC
试说明:ED⊥AB如图,已知BD、CE为△ABC的高,试说明:∠ADE=∠ABC. 要做两个形状相同的三角形框架,其中一个三角形框架的三边的长分别为4、5、6,另一个三角形框架的一边长为2,请你想一想应该怎样选择材料可使这两个三角形相似? 你选的材料唯一吗?小结两个三角形相似的判定方法:(1)两角对应相等的 两个三角形相似.
(2)三边对应成比例的 两个三角形相似.
(3) 两边对应成比例且夹角相等的两个三角形相似.
