1.2 数轴、相反数和绝对值 沪科版版数学七年级上册
文档属性
| 名称 | 1.2 数轴、相反数和绝对值 沪科版版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 06:28:10 | ||
图片预览






文档简介
(共47张PPT)
沪科版数学七年级上册
第1章 有理数
第一课时 数轴
1.2 数轴、相反数和绝对值
学习目标
1.掌握数轴的三要素,能正确画出数轴.
2.能将已知数在数轴上表示出来,能说出数轴上已知点所表示的数.
3.掌握数轴的概念,理解数轴上的点和有理数的对应关系.
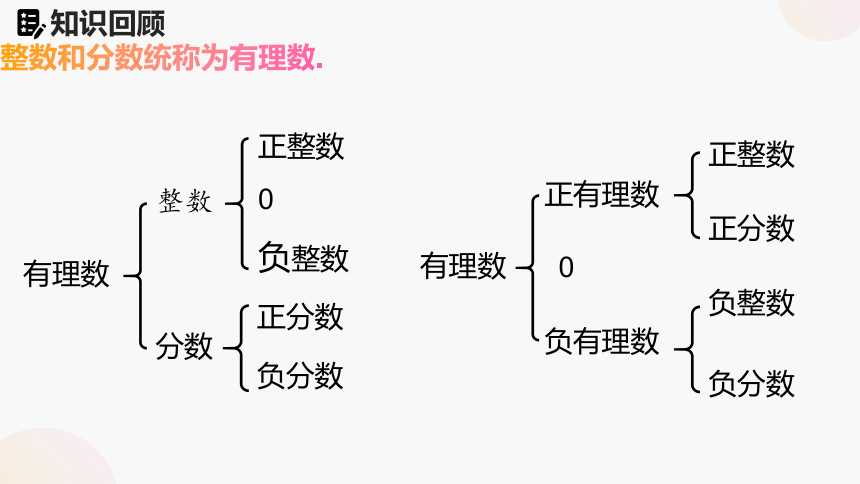
整数和分数统称为有理数.
有理数
整数
正整数
0
负整数
正分数
负分数
分数
有理数
正有理数
正整数
0
负整数
正分数
负分数
负有理数
知识回顾
课堂导入
观察温度计,在温度计上可以表示出 5 ℃,-10℃ 及 0℃.
课堂导入
机器人在一条东西向的直路上做走步取物试验. 根据指令,它由点 O 处出发,向西走 3 m 到达点 A 处,拿取物品,然后,返回点 O 处将物品放入篮中,再向东走 2 m 到达点 B 处取物.
课堂导入
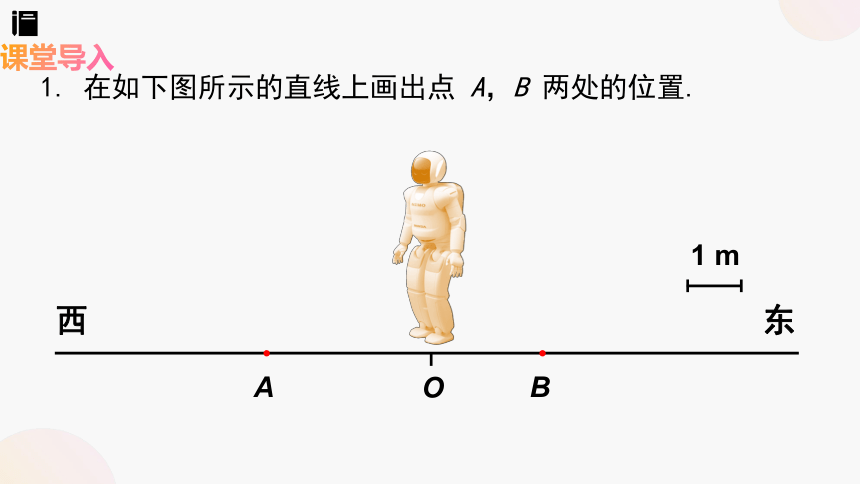
1. 在如下图所示的直线上画出点 A,B 两处的位置.
O
西
东
1 m
A
B
课堂导入
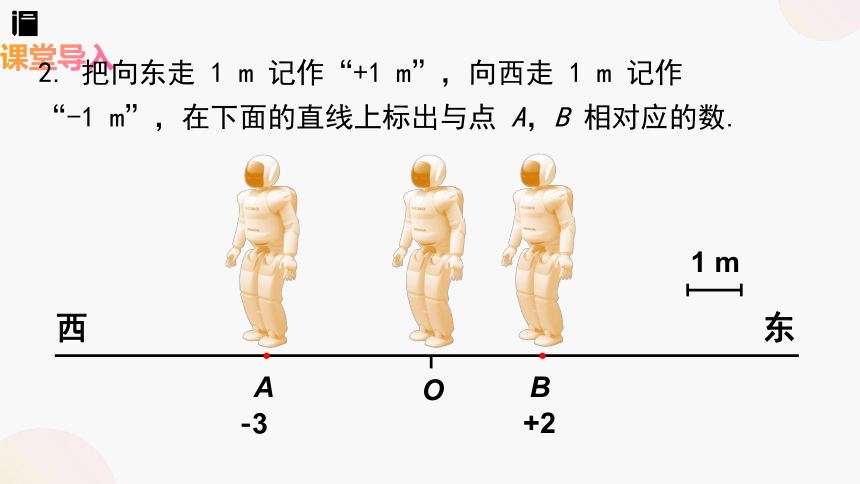
2. 把向东走 1 m 记作“+1 m”,向西走 1 m 记作
“-1 m”,在下面的直线上标出与点 A,B 相对应的数.
O
西
东
1 m
A
B
-3
+2
新知探究
通过上述例子,由此联想,我们是否可以用一条直线上的一些点表示有理数?
思考
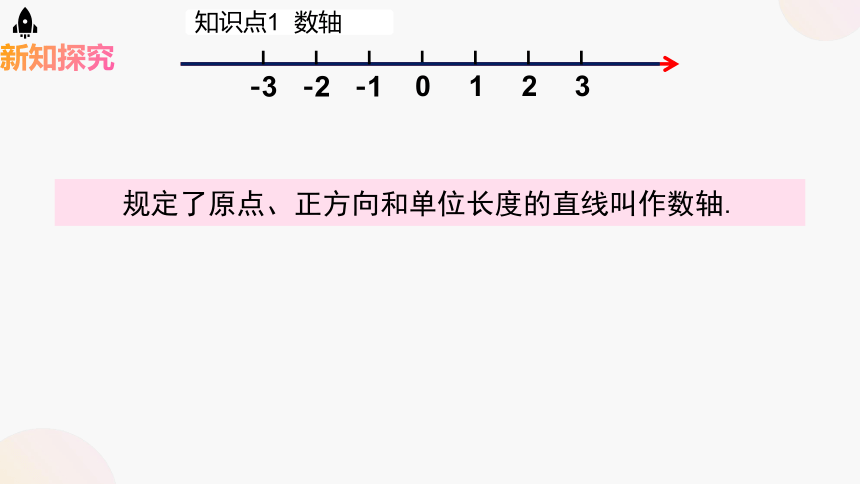
知识点1 数轴
新知探究
(1)画一条直线,在这条直线上任取一点作为原点,用这点表示数 0;
(2)规定这条直线的一个方向为正方向,相反的方向就是负方向. 当直线水平放置时,一般取从左到右的方向为正方向,并用箭头表示;
(3)适当选取某一长度作为单位长度.
0
-1
-2
-3
1
2
3
知识点1 数轴
新知探究
0
-1
-2
-3
1
2
3
规定了原点、正方向和单位长度的直线叫作数轴.
知识点1 数轴
新知探究
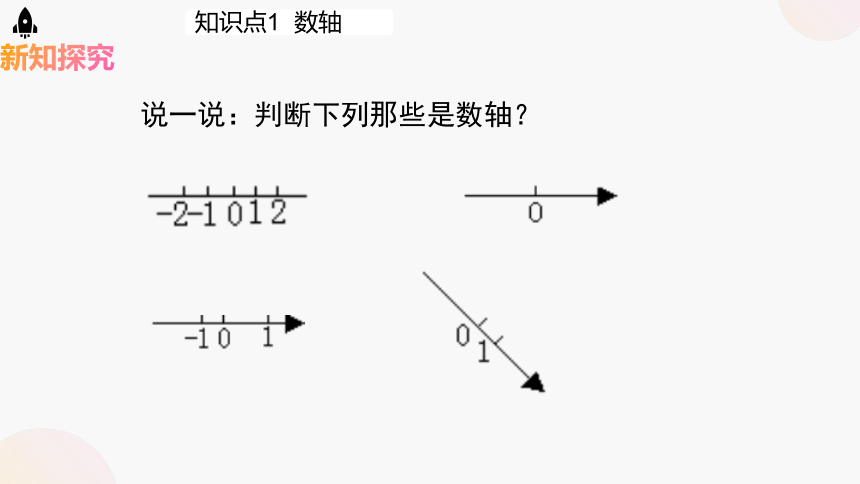
说一说:判断下列那些是数轴?
知识点1 数轴
新知探究
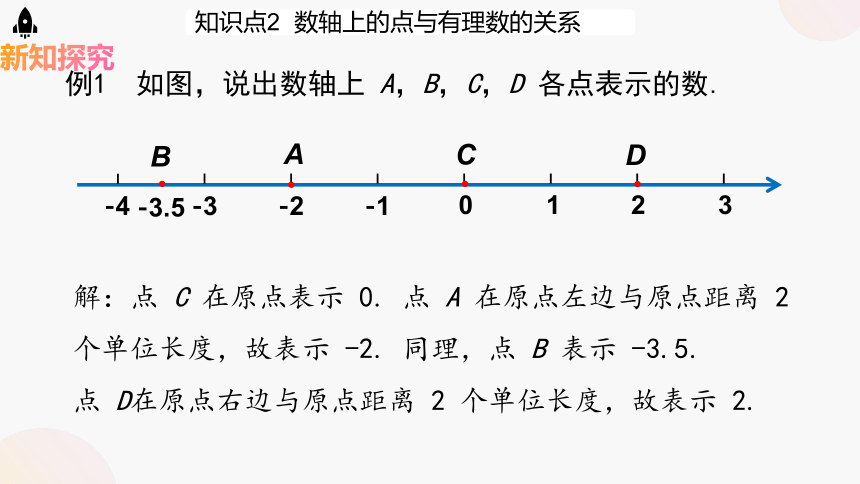
例1 如图,说出数轴上 A,B,C,D 各点表示的数.
解:点 C 在原点表示 0. 点 A 在原点左边与原点距离 2 个单位长度,故表示 -2. 同理,点 B 表示 -3.5.
点 D在原点右边与原点距离 2 个单位长度,故表示 2.
0
1
2
-1
B
A
C
D
-3.5
3
-2
-3
-4
知识点2 数轴上的点与有理数的关系
新知探究
解:+4用数轴上位于原点右边与原点距离 4 个单位长度的点表示,-4用数轴上位于原点左边与原点距离 4 个单位长度的点表示. 同理,可以画出表示 , ,-1.25 的点.
例 2 在数轴上画出表示下列各数的点:
+4, , ,-1.25,-4
﹣1
﹣2
﹣3
﹣4
-1.25
知识点2 数轴上的点与有理数的关系
新知探究
0
1
2
﹣1
﹣2
﹣3
﹣4
3
4
-1.25
一般地,任意一个有理数,都可以用数轴上的一个点来表示.
知识点2 数轴上的点与有理数的关系
随堂练习
1. 点 A,B,C,D 在数轴上的位置如图:
5
0
1
2
-1
-2
-3
-4
3
4
6
A
B
C
D
-3.5,-2,2.5,5
A,B,C,D 四个点分别表示数_________________.
【教材P9 练习 第1题】
随堂练习
2.在数轴上画出表示﹣3,﹢2,﹣1.5,﹣6.5的点.
0
1
2
3
﹣1
﹣2
﹣3
﹣4
﹣5
﹣6
4
5
6
﹣7
﹣3
﹢2
﹣1.5
﹣6.5
【教材P10 练习 第2题】
有理数
数轴
原 点
单位长度
数与点
的转化
三要素
正方向
课堂小结
沪科版数学七年级上册
第1章 有理数
第二课时 相反数
1.2 数轴、相反数和绝对值
学习目标
1.借助数轴理解相反数的意义,体会数形结合的思想方法,会求一个数的相反数;
2.会对含多重符号的有理数进行化简.
新知探究
在数轴上找到表示 2 与﹣2,4与﹣4, 与 的点.
0
1
2
3
﹣1
﹣2
﹣3
﹣4
﹣5
4
5
1. 这三组点各有什么相同点和不同点?
2. 它们在数轴上的位置有什么关系?
知识点 相反数
新知探究
0
1
2
3
﹣1
﹣2
﹣3
﹣4
﹣5
4
5
由上可知,2与﹣2,4与﹣4, 与 都只有符号不同.
只有符号不同的两个数互为相反数. 这就是说,其中一个数是另一个数的相反数.
知识点 相反数
新知探究
数 a 的相反数是 -a,这里 a 表示任意一个数,它可以是正数、负数或者 0.
归纳
特别规定:0 的相反数是 0.
知识点 相反数
新知探究
不为0的数与它的相反数在数轴上所表示的点在原点的两侧,与原点的距离相等.
﹣4
4
0
4与﹣4互为相反数
相等
知识点 相反数
新知探究
例1 写出下列各数的相反数:
3,﹣7,﹣2.1, , ,0,20.
解 : 3的相反数是﹣3,﹣7的相反数是7,﹣2.1的相反数是2.1, 的相反数是 , 的相反数是 ,0的相反数是0,20的相反数是﹣20.
知识点 相反数
新知探究
在任意一个数前面添上“﹣”号,所得的数就是原数的相反数,如 -(+3) = -3,-(-3) = 3,-0 = 0.
归纳
知识点 相反数
新知探究
1.3的相反数是 ;
﹣6的相反数是 ;
的相反数是 ;
﹣(﹣3)= ;
﹣(﹣0.8)= ;
= .
﹣1.3
6
3
0.8
说一说
知识点 相反数
随堂练习
1. 分别写出下列各数的相反数:
﹣5,1,﹣3,﹣2.6,1.2,﹣0.9, .
5
﹣1
3
2.6
﹣1.2
0.9
【教材P11 练习 第1题】
随堂练习
2. 填空:
(1)﹣2.8是____的相反数,____的相反数是3.2;
(2)﹣ (﹢4)是____的相反数,﹣ (﹣7)是____的相反数;
(3)﹣ (﹢8)=____,﹣ (﹣9)=____.
2.8
﹣3.2
4
﹣7
﹣8
9
【教材P11 练习 第2题】
3. 下列说法不正确的是( )
A.一个正数的相反数是负数,一个负数的相反数是正数
B.在数轴上与原点距离相等但不重合的两个点,所表示的数一定互为相反数
C.符号不同的两个数互为相反数
D.两个数互为相反数,这两个数有可能相等
C
【教材P11 练习 第3题】
随堂练习
课堂小结
相反数
在原数前面加“-”号
求法
定义
多重符号的化简
相反数的几何意义
沪科版数学七年级上册
第1章 有理数
第三课时 绝对值
1.2 数轴、相反数和绝对值
学习目标
1.知道绝对值的意义,会求一个数的绝对值;
2.掌握绝对值的性质,会利用绝对值的性质解决相关问题.
新知探究
0
- 10
10
O
东
小红和小明从同一处O出发,分别向东、西方向行走10米,他们行走的方向相同吗?他们行走的路程相同吗?
10
10
上述这个问题反映了什么数学知识?
知识点1 绝对值的定义
新知探究
在数轴上,表示 4 与 -4 的点与原点的距离各是多少?表示 与 的点与原点的距离各是多少?
知识点1 绝对值的定义
观察
新知探究
在数轴上,表示数 a 的点与原点的距离叫作数 a 的绝对值,记作|a|.
这里的数a可以是正数、负数和0.
0
1
2
3
﹣1
﹣2
﹣3
﹣4
﹣5
4
5
|-4|
|4|
+4和-4符号相反,表示它们的点位于原点的两侧,但与原点的距离都等于4,即它们的绝对值都是4,记作|+4|=4,
|-4|=4.
知识点1 绝对值的定义
新知探究
由绝对值的定义可知:
(1)一个正数的绝对值是它本身;
(2)一个负数的绝对值是它的相反数;
(3)0 的绝对值是 0.
即
a, a > 0,
0, a = 0,
- a, a < 0.
| a | =
知识点2 绝对值的性质
新知探究
讨论下面3个问题:
(1)有没有绝对值等于﹣2 的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数 a 取何值,它的绝对值总是什么数?
不论有理数 a 取何值,它的绝对值总是正数或 0(非负数),即对任意有理数 a,总有 | a | ≥ 0.
知识点2 绝对值的性质
新知探究
例1 判断:
Ⅰ.若 a = ﹣a,则a<0. ( )
Ⅱ.绝对值等于它本身的数一定是正数. ( )
Ⅲ.绝对值最小的数是 1. ( )
Ⅳ.任何有理数的绝对值都是正数. ( )
×
×
a = 0
还有 0
×
×
0 的绝对值是 0,但 0 不是正数
知识点2 绝对值的性质
新知探究
交流:互为相反数的两个数的绝对值有什么关系?
分析:一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.
结论:互为相反数的两个数的绝对值相等.
知识点2 绝对值的性质
新知探究
例2 求下列各数的绝对值:
,﹢1,﹣0.1,4.5.
解:
|﹢1|=1,
|﹣0.1|=0.1,
|4.5|=4.5.
知识点2 绝对值的性质
随堂练习
6,﹣8,﹣0.9, , , 100, 0.
|6|=6;
|﹣8|=8;
|﹣0.9|=0.9;
|100|=100;
|0|=0.
解:
1.写出下列各数的绝对值:
随堂练习
2.在数轴上画出表示出下列各数的点,并指出它们的绝对值:
,﹣2,0,﹣0.5,7.
0
-2
-1
1
2
3
4
5
6
7
-0.5
【教材P12 练习 第1题】
|-2|=2;
|7|=7.
|﹣0.5|=0.5;
|0|=0;
【教材P12 练习 第2题】
3.填空
| -3 |=____,| 1.5 | =____,| 0 | =____,
| -0.02 | =_____,| | =____,| | =____.
3
1.5
0
0.02
随堂练习
4.下列等式中不成立的是( )
(A)|﹣5|= 5 (B)﹣|5|= ﹣|﹣5|
(C)|﹣5|=|5| (D)﹣|﹣5|= 5
D
【教材P12 练习 第3题】
随堂练习
5. 计算
(1)|﹣8|+|9|
(2)|﹣12|÷|12|
(3)|0.6|-| |
(4)|﹣3|×|﹣2|
=17
=1
=0
=6
【教材P12 练习 第4题】
随堂练习
课堂小结
绝对值的性质
绝对值的意义
绝对值
数轴上表示数 a 的点与原点的距离.
|a|=
谢谢观看
Thank you
沪科版数学七年级上册
第1章 有理数
第一课时 数轴
1.2 数轴、相反数和绝对值
学习目标
1.掌握数轴的三要素,能正确画出数轴.
2.能将已知数在数轴上表示出来,能说出数轴上已知点所表示的数.
3.掌握数轴的概念,理解数轴上的点和有理数的对应关系.
整数和分数统称为有理数.
有理数
整数
正整数
0
负整数
正分数
负分数
分数
有理数
正有理数
正整数
0
负整数
正分数
负分数
负有理数
知识回顾
课堂导入
观察温度计,在温度计上可以表示出 5 ℃,-10℃ 及 0℃.
课堂导入
机器人在一条东西向的直路上做走步取物试验. 根据指令,它由点 O 处出发,向西走 3 m 到达点 A 处,拿取物品,然后,返回点 O 处将物品放入篮中,再向东走 2 m 到达点 B 处取物.
课堂导入
1. 在如下图所示的直线上画出点 A,B 两处的位置.
O
西
东
1 m
A
B
课堂导入
2. 把向东走 1 m 记作“+1 m”,向西走 1 m 记作
“-1 m”,在下面的直线上标出与点 A,B 相对应的数.
O
西
东
1 m
A
B
-3
+2
新知探究
通过上述例子,由此联想,我们是否可以用一条直线上的一些点表示有理数?
思考
知识点1 数轴
新知探究
(1)画一条直线,在这条直线上任取一点作为原点,用这点表示数 0;
(2)规定这条直线的一个方向为正方向,相反的方向就是负方向. 当直线水平放置时,一般取从左到右的方向为正方向,并用箭头表示;
(3)适当选取某一长度作为单位长度.
0
-1
-2
-3
1
2
3
知识点1 数轴
新知探究
0
-1
-2
-3
1
2
3
规定了原点、正方向和单位长度的直线叫作数轴.
知识点1 数轴
新知探究
说一说:判断下列那些是数轴?
知识点1 数轴
新知探究
例1 如图,说出数轴上 A,B,C,D 各点表示的数.
解:点 C 在原点表示 0. 点 A 在原点左边与原点距离 2 个单位长度,故表示 -2. 同理,点 B 表示 -3.5.
点 D在原点右边与原点距离 2 个单位长度,故表示 2.
0
1
2
-1
B
A
C
D
-3.5
3
-2
-3
-4
知识点2 数轴上的点与有理数的关系
新知探究
解:+4用数轴上位于原点右边与原点距离 4 个单位长度的点表示,-4用数轴上位于原点左边与原点距离 4 个单位长度的点表示. 同理,可以画出表示 , ,-1.25 的点.
例 2 在数轴上画出表示下列各数的点:
+4, , ,-1.25,-4
﹣1
﹣2
﹣3
﹣4
-1.25
知识点2 数轴上的点与有理数的关系
新知探究
0
1
2
﹣1
﹣2
﹣3
﹣4
3
4
-1.25
一般地,任意一个有理数,都可以用数轴上的一个点来表示.
知识点2 数轴上的点与有理数的关系
随堂练习
1. 点 A,B,C,D 在数轴上的位置如图:
5
0
1
2
-1
-2
-3
-4
3
4
6
A
B
C
D
-3.5,-2,2.5,5
A,B,C,D 四个点分别表示数_________________.
【教材P9 练习 第1题】
随堂练习
2.在数轴上画出表示﹣3,﹢2,﹣1.5,﹣6.5的点.
0
1
2
3
﹣1
﹣2
﹣3
﹣4
﹣5
﹣6
4
5
6
﹣7
﹣3
﹢2
﹣1.5
﹣6.5
【教材P10 练习 第2题】
有理数
数轴
原 点
单位长度
数与点
的转化
三要素
正方向
课堂小结
沪科版数学七年级上册
第1章 有理数
第二课时 相反数
1.2 数轴、相反数和绝对值
学习目标
1.借助数轴理解相反数的意义,体会数形结合的思想方法,会求一个数的相反数;
2.会对含多重符号的有理数进行化简.
新知探究
在数轴上找到表示 2 与﹣2,4与﹣4, 与 的点.
0
1
2
3
﹣1
﹣2
﹣3
﹣4
﹣5
4
5
1. 这三组点各有什么相同点和不同点?
2. 它们在数轴上的位置有什么关系?
知识点 相反数
新知探究
0
1
2
3
﹣1
﹣2
﹣3
﹣4
﹣5
4
5
由上可知,2与﹣2,4与﹣4, 与 都只有符号不同.
只有符号不同的两个数互为相反数. 这就是说,其中一个数是另一个数的相反数.
知识点 相反数
新知探究
数 a 的相反数是 -a,这里 a 表示任意一个数,它可以是正数、负数或者 0.
归纳
特别规定:0 的相反数是 0.
知识点 相反数
新知探究
不为0的数与它的相反数在数轴上所表示的点在原点的两侧,与原点的距离相等.
﹣4
4
0
4与﹣4互为相反数
相等
知识点 相反数
新知探究
例1 写出下列各数的相反数:
3,﹣7,﹣2.1, , ,0,20.
解 : 3的相反数是﹣3,﹣7的相反数是7,﹣2.1的相反数是2.1, 的相反数是 , 的相反数是 ,0的相反数是0,20的相反数是﹣20.
知识点 相反数
新知探究
在任意一个数前面添上“﹣”号,所得的数就是原数的相反数,如 -(+3) = -3,-(-3) = 3,-0 = 0.
归纳
知识点 相反数
新知探究
1.3的相反数是 ;
﹣6的相反数是 ;
的相反数是 ;
﹣(﹣3)= ;
﹣(﹣0.8)= ;
= .
﹣1.3
6
3
0.8
说一说
知识点 相反数
随堂练习
1. 分别写出下列各数的相反数:
﹣5,1,﹣3,﹣2.6,1.2,﹣0.9, .
5
﹣1
3
2.6
﹣1.2
0.9
【教材P11 练习 第1题】
随堂练习
2. 填空:
(1)﹣2.8是____的相反数,____的相反数是3.2;
(2)﹣ (﹢4)是____的相反数,﹣ (﹣7)是____的相反数;
(3)﹣ (﹢8)=____,﹣ (﹣9)=____.
2.8
﹣3.2
4
﹣7
﹣8
9
【教材P11 练习 第2题】
3. 下列说法不正确的是( )
A.一个正数的相反数是负数,一个负数的相反数是正数
B.在数轴上与原点距离相等但不重合的两个点,所表示的数一定互为相反数
C.符号不同的两个数互为相反数
D.两个数互为相反数,这两个数有可能相等
C
【教材P11 练习 第3题】
随堂练习
课堂小结
相反数
在原数前面加“-”号
求法
定义
多重符号的化简
相反数的几何意义
沪科版数学七年级上册
第1章 有理数
第三课时 绝对值
1.2 数轴、相反数和绝对值
学习目标
1.知道绝对值的意义,会求一个数的绝对值;
2.掌握绝对值的性质,会利用绝对值的性质解决相关问题.
新知探究
0
- 10
10
O
东
小红和小明从同一处O出发,分别向东、西方向行走10米,他们行走的方向相同吗?他们行走的路程相同吗?
10
10
上述这个问题反映了什么数学知识?
知识点1 绝对值的定义
新知探究
在数轴上,表示 4 与 -4 的点与原点的距离各是多少?表示 与 的点与原点的距离各是多少?
知识点1 绝对值的定义
观察
新知探究
在数轴上,表示数 a 的点与原点的距离叫作数 a 的绝对值,记作|a|.
这里的数a可以是正数、负数和0.
0
1
2
3
﹣1
﹣2
﹣3
﹣4
﹣5
4
5
|-4|
|4|
+4和-4符号相反,表示它们的点位于原点的两侧,但与原点的距离都等于4,即它们的绝对值都是4,记作|+4|=4,
|-4|=4.
知识点1 绝对值的定义
新知探究
由绝对值的定义可知:
(1)一个正数的绝对值是它本身;
(2)一个负数的绝对值是它的相反数;
(3)0 的绝对值是 0.
即
a, a > 0,
0, a = 0,
- a, a < 0.
| a | =
知识点2 绝对值的性质
新知探究
讨论下面3个问题:
(1)有没有绝对值等于﹣2 的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数 a 取何值,它的绝对值总是什么数?
不论有理数 a 取何值,它的绝对值总是正数或 0(非负数),即对任意有理数 a,总有 | a | ≥ 0.
知识点2 绝对值的性质
新知探究
例1 判断:
Ⅰ.若 a = ﹣a,则a<0. ( )
Ⅱ.绝对值等于它本身的数一定是正数. ( )
Ⅲ.绝对值最小的数是 1. ( )
Ⅳ.任何有理数的绝对值都是正数. ( )
×
×
a = 0
还有 0
×
×
0 的绝对值是 0,但 0 不是正数
知识点2 绝对值的性质
新知探究
交流:互为相反数的两个数的绝对值有什么关系?
分析:一对相反数虽然分别在原点两边,但它们到原点的距离是相等的.
结论:互为相反数的两个数的绝对值相等.
知识点2 绝对值的性质
新知探究
例2 求下列各数的绝对值:
,﹢1,﹣0.1,4.5.
解:
|﹢1|=1,
|﹣0.1|=0.1,
|4.5|=4.5.
知识点2 绝对值的性质
随堂练习
6,﹣8,﹣0.9, , , 100, 0.
|6|=6;
|﹣8|=8;
|﹣0.9|=0.9;
|100|=100;
|0|=0.
解:
1.写出下列各数的绝对值:
随堂练习
2.在数轴上画出表示出下列各数的点,并指出它们的绝对值:
,﹣2,0,﹣0.5,7.
0
-2
-1
1
2
3
4
5
6
7
-0.5
【教材P12 练习 第1题】
|-2|=2;
|7|=7.
|﹣0.5|=0.5;
|0|=0;
【教材P12 练习 第2题】
3.填空
| -3 |=____,| 1.5 | =____,| 0 | =____,
| -0.02 | =_____,| | =____,| | =____.
3
1.5
0
0.02
随堂练习
4.下列等式中不成立的是( )
(A)|﹣5|= 5 (B)﹣|5|= ﹣|﹣5|
(C)|﹣5|=|5| (D)﹣|﹣5|= 5
D
【教材P12 练习 第3题】
随堂练习
5. 计算
(1)|﹣8|+|9|
(2)|﹣12|÷|12|
(3)|0.6|-| |
(4)|﹣3|×|﹣2|
=17
=1
=0
=6
【教材P12 练习 第4题】
随堂练习
课堂小结
绝对值的性质
绝对值的意义
绝对值
数轴上表示数 a 的点与原点的距离.
|a|=
谢谢观看
Thank you
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
