1.6 有理数的乘方 沪科版版数学七年级上册
文档属性
| 名称 | 1.6 有理数的乘方 沪科版版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 00:00:00 | ||
图片预览











文档简介
(共47张PPT)
沪科版数学七年级上册
第1章 有理数
第一课时 有理数的乘方
1.6 有理数的乘方
学习目标
1.知道有理数乘方的意义,能说出乘方运算、幂、底数、指数等概念.
2.能正确进行有理数的乘方运算.
知识点1 乘方的定义
问题:
若对折10次可裁成几张?请用一个算式表示(不用算出结果)
若对折100次,算式中有几个2相乘?
对折2次可裁成4张,即2×2张;
对折3次可裁成8张,即2×2×2张.
试一试:将一张纸按下列要求对折。
新知探究
新知探究
对折10次裁成的张数用以下算式计算2×2×2×2×2×2×2×2×2×2
是一个有10个2相乘的乘积式;
对折100次裁成的张数,可用算式
计算,在这个积中有100个2相乘。
这么长的算式有简单的记法吗?
知识点1 乘方的定义
新知探究
如图,边长为 5 的正方形,它的面积是 5×5 = 25,5×5 可记作_____.
如图,棱长为 2 的正方体,它的体积是 2×2×2 = 8,2×2×2 可记作_____.
52
23
知识点1 乘方的定义
a · a · a · … · a 可记作:____,即a · a · a · … · a=____.
2 ×2 × 2 × 2 可记作: ,
2 ×2 × 2 × 2 × 2 可记 作: ,
2×2×···×2
n个2
可记作: ,
n个a
n个a
24
25
2n
an
an
想一想:上面各式具有什么共同特征?
知识点1 乘方的定义
新知探究
猜想
n个相同的因数a相乘,即
这种求n个 的积的运算,叫作乘方。
相同因数
我们把它记作an,
即
乘方的结果叫作幂。
在an中,a叫作底数,n叫作a的幂的指数,简称指数。
an 读作a的n次方,也可以读作a的n次幂。
知识点1 乘方的定义
新知探究
新知探究
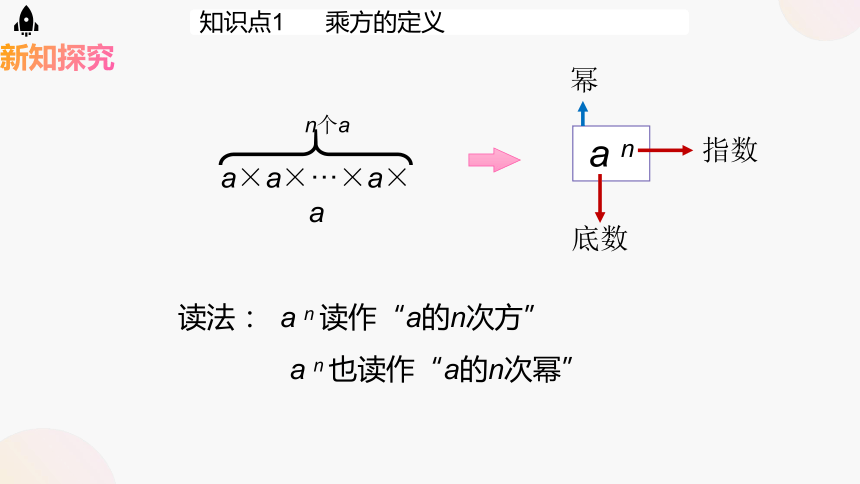
知识点1 乘方的定义
a×a×···×a×a
n个a
a n
底数
指数
幂
读法: a n 读作“a的n次方”
a n 也读作“a的n次幂”
新知探究
在幂56中,底数是 ,指数是 ;读作:
在幂45中,底数是 ,指数是 ;
读作: .
5
6
5的6次方
4
5
4的5次方
知识点1 乘方的定义
说一说
一个数的一次方,就是这个数本身,指数1通常省略不写.
2次方又叫平方,3次方又叫立方。
例如:51就是5.
知识点1 乘方的定义
新知探究
注意
议一议
(–3)4 与 –34 相同吗?
知识点2 负数的幂的正负与指数的关系
新知探究
(–3)4 = 81
是 的相反数,而
读作负三的四次方.
–34
34
(–3)
4
–34 = –81
知识点2 负数的幂的正负与指数的关系
新知探究
知识点2 负数的幂的正负与指数的关系
例1 计算:
(1)(-4)3 ; (2)(-2)4.
解:(1)(-4)3=(-4)×(-4)×(-4)= .
(2)(-2)4= = .
(-2)×(-2)×(-2)×(-2)
-64
16
用计算器
怎么算呢?
非0有理数的乘方结果符号:正数的任何次乘方都取正号;负数的奇次乘方取负号,负数的偶次乘方取正号.
新知探究
知识点2 负数的幂的正负与指数的关系
用计算器按下列顺序计算:
按键顺序 显示
-64
16
(
(-)
4
)
x3
=
(
(-)
2
)
=
4
新知探究
新知探究
把下列相同因数的乘积写成幂的形式,并说出底数和指数:
(1) (-6)×(-6) ×(-6)
底数是 –6,指数是 3
(2)
底数是
,指数是 4
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
知识点2 负数的幂的正负与指数的关系
新知探究
(3)在1210中,12是 数,10是___数,
读作 ;
(4) 的底数是 ,指数是 ,读作
;
7
底
指
12的10次方
的7次方
知识点2 负数的幂的正负与指数的关系
新知探究
乘方运算实际上就是乘法运算,根据有理数的乘法法则,可得乘方运算的法则:
求非 0 有理数的乘方,将其绝对值乘方,并取符号:正数的任意次幂都取正号;负数的奇次幂取负号,负数的偶次幂取正号.
新知探究
交 流
拉面师傅制作拉面时,按对折、拉伸的步骤,重复多次.
(1)先用乘法计算拉 12 次得到的面条数,再改用计算器计算幂,这两种方法哪种算得快?
用计算器计算幂算得快
212 = 4096
新知探究
(2)如果拉面师傅每次拉伸面条的长度为 0.8 m,那么拉 12 次后,得到的面条总长是多少米?
0.8×212 = 3276.8 (m)
随堂练习
2. 填空:
(1)在 74 中,底数是_____,指数是_____;
(2)在 中,底数是_____,指数是_____.
7
4
5
【教材P44 练习 第2题】
随堂练习
3. 计算:
(1)(-1.5)2; (2)4×(-2)3;
(3)-(-2)4; (4)(-2)3×(-2)2.
2.25
-32
-16
-32
【教材P44 练习 第3题】
课堂小结
根据有理数的乘法法则可以得出:
1.负数的奇次幂是负数,负数的偶次幂是正数;
2. 正数的任何次幂都是正数;
3. 0的任何正整数次幂都是0.
一般地,n个相同的乘数a相乘,记作 an,读作“a的n次方”.
求n个相同乘数的积的运算,叫作乘方,乘方的结果叫作幂.
乘方
沪科版数学七年级上册
第1章 有理数
第二课时 有理数的混合运算
1.6 有理数的乘方
学习目标
1.知道有理数加、减、乘、除、乘方混合运算的运算顺序.
2.会进行有理数的混合运算.
新知探究
在进行有理数的加、减、乘、除以及乘方混合运算时,一般应按下列顺序进行:
先乘方,再乘除,后加减;如果有括号,先进行括号里的运算.
知识点 有理数的混合运算
新知探究
例1 计算:
(1)-10 + 8÷(-2)2-(-4)×(-3);
解 (1) -10 + 8÷(-2)2-(-4)×(-3)
= -10 + 8÷4-4×3
= -10 + 2-12
= -20
知识点 有理数的混合运算
知识点 有理数的混合运算
(2) .
新知探究
随堂练习
1. 计算:
(1)-23-3×(-1)3-(-1)4;
解 -23-3×(-1)3-(-1)4
= -8-3×(-1)-1
= - 8 + 3 - 1
= - 6
【教材P45 练习 第1题】
(2) .
随堂练习
2. 计算:
(1) ;
解
【教材P45 练习 第2题】
随堂练习
沪科版数学七年级上册
第1章 有理数
第三课时 科学记数法
1.6 有理数的乘方
学习目标
1.了解科学记数法的现实意义,学会用科学记数法表示较大的数.
2.会用科学记数法表示的数进行简单的运算.
课堂导入
在日常生活中,常会接触到一些比较大的数,如长江三峡水库容量达 39 300 000 000 m3,光在空气中传播的速度大约是 300 000 000 m/s.
(1)长江三峡水库
(2)光的传播
课堂导入
39 300 000 000 300 000 000
这些较大的数,按上面的写法,写起来既麻烦又容易出错. 于是我们常用更大的数量级来表示,如将 39 300 000 000 表示为 393 亿.
你还知道其他的表示方法吗?
新知探究
10的乘方有如下的特点:
一般地,10的n次幂等于10···0(在1的后面有n个0),所以就可以用10的幂来表示一些大数.
你知道101,102,103,104分别等于多少吗?
的意义和规律是什么?
知识点 用科学记数法表示数
新知探究
书写简短,便于读数.
读作:5.67 乘 10 的8次方(幂)
例如:567 000 000
6 100 000 000 = 6.1×1 000 000 000
= 6.1×109
= 5.67×100 000 000
=5.67×
22 600 000 000 = 2.26×10 000 000 000
= 2.26×
知识点 用科学记数法表示数
新知探究
一般地,绝对值大于 10 的数都可记成 ±a×10n 的形式,其中 1≤a<10,n等于原数的整数位数减1. 这种记数方法,在科学技术方面是常用的,习惯上称之为科学记数法.
知识点 用科学记数法表示数
例1《2020 年全球森林资源评估》报告指出:1990 年以来,全球因砍伐而丧失了约 4.2 亿公顷森林,但森林丧失的速度已大幅下降,2015 至 2020 年,每年因砍伐而丧失的森林面积约为 1 000 万公顷. 请用科学记数法表示 4.2 亿 和 1 000 万,并用计算器表示.
解 4.2 亿 = 420 000 000 = 4.2×108.
1 000 万= 10 000 000 = 1×107.
知识点 用科学记数法表示数
新知探究
试一试 用科学记数法表示下列各数:
1×106.
-1.23×1011.
1 000 000,57 000 000,-123 000 000 000.
解:
1 000 000 =
-123 000 000 000 =
5.7×107.
57 000 000 =
知识点 用科学记数法表示数
新知探究
新知探究
5.7×107.
-1.23×1011.
57 000 000 =
-123 000 000 000 =
思考:
等号左边整数的位数与右边10的指数有什么关系?
用科学记数法表示一个n 位整数时,10的指数是 .
知识点 用科学记数法表示数
知识点 用科学记数法表示数
例2 下列各数是否用科学记数法表示的?为什么?
不是
2 400 000
2 400 000
3 100 000
3 100 000
不是
新知探究
随堂练习
1. 用科学记数法表示下列各数:
10 000,800 000,56 000 000,7 400 000.
解 10 000 = 1×104
800 000 = 8×105
56 000 000 = 5.6×107
7 400 000 = 7.4×106
【教材P46 练习 第1题】
2. 下列用科学记数法表示的数原来分别是什么数?
1×107,4×103,8.5×106,7.04×105.
解 1×107 = 10 000 000
4×103 = 4 000
8.5×106 =8 500 000
7.04×105 = 704 000
【教材P46 练习 第2题】
随堂练习
3. 截至 2022 年 12 月 31日,中国共产党党员总数为 9804.1 万名,用科学记数法表示 9804.1 万.
解 9804.1 万 = 98 041 000 = 9.8041×107
【教材P46 练习 第3题】
随堂练习
4. 从 2012 年到 2021 年,我国国内生产总值从 54 万亿元增长到 114 万亿元. 试用科学记数法表示 54 万亿和 114 万亿.
54 万亿 = 54 000 000 000 000 = 5.4×1013
114 万亿 = 114 000 000 000 000 = 1.14×1014
【教材P46 练习 第4题】
课堂小结
用科学记数法表示一个n位整数(n ≥2),其中10的指数是n-1.
科学记数法
把一个大于10的数表示成 a×10n 的形式(其中a 大于或等于1,且a 小于10,n是正整数),这种记法是科学记数法.
谢谢观看
Thank you
沪科版数学七年级上册
第1章 有理数
第一课时 有理数的乘方
1.6 有理数的乘方
学习目标
1.知道有理数乘方的意义,能说出乘方运算、幂、底数、指数等概念.
2.能正确进行有理数的乘方运算.
知识点1 乘方的定义
问题:
若对折10次可裁成几张?请用一个算式表示(不用算出结果)
若对折100次,算式中有几个2相乘?
对折2次可裁成4张,即2×2张;
对折3次可裁成8张,即2×2×2张.
试一试:将一张纸按下列要求对折。
新知探究
新知探究
对折10次裁成的张数用以下算式计算2×2×2×2×2×2×2×2×2×2
是一个有10个2相乘的乘积式;
对折100次裁成的张数,可用算式
计算,在这个积中有100个2相乘。
这么长的算式有简单的记法吗?
知识点1 乘方的定义
新知探究
如图,边长为 5 的正方形,它的面积是 5×5 = 25,5×5 可记作_____.
如图,棱长为 2 的正方体,它的体积是 2×2×2 = 8,2×2×2 可记作_____.
52
23
知识点1 乘方的定义
a · a · a · … · a 可记作:____,即a · a · a · … · a=____.
2 ×2 × 2 × 2 可记作: ,
2 ×2 × 2 × 2 × 2 可记 作: ,
2×2×···×2
n个2
可记作: ,
n个a
n个a
24
25
2n
an
an
想一想:上面各式具有什么共同特征?
知识点1 乘方的定义
新知探究
猜想
n个相同的因数a相乘,即
这种求n个 的积的运算,叫作乘方。
相同因数
我们把它记作an,
即
乘方的结果叫作幂。
在an中,a叫作底数,n叫作a的幂的指数,简称指数。
an 读作a的n次方,也可以读作a的n次幂。
知识点1 乘方的定义
新知探究
新知探究
知识点1 乘方的定义
a×a×···×a×a
n个a
a n
底数
指数
幂
读法: a n 读作“a的n次方”
a n 也读作“a的n次幂”
新知探究
在幂56中,底数是 ,指数是 ;读作:
在幂45中,底数是 ,指数是 ;
读作: .
5
6
5的6次方
4
5
4的5次方
知识点1 乘方的定义
说一说
一个数的一次方,就是这个数本身,指数1通常省略不写.
2次方又叫平方,3次方又叫立方。
例如:51就是5.
知识点1 乘方的定义
新知探究
注意
议一议
(–3)4 与 –34 相同吗?
知识点2 负数的幂的正负与指数的关系
新知探究
(–3)4 = 81
是 的相反数,而
读作负三的四次方.
–34
34
(–3)
4
–34 = –81
知识点2 负数的幂的正负与指数的关系
新知探究
知识点2 负数的幂的正负与指数的关系
例1 计算:
(1)(-4)3 ; (2)(-2)4.
解:(1)(-4)3=(-4)×(-4)×(-4)= .
(2)(-2)4= = .
(-2)×(-2)×(-2)×(-2)
-64
16
用计算器
怎么算呢?
非0有理数的乘方结果符号:正数的任何次乘方都取正号;负数的奇次乘方取负号,负数的偶次乘方取正号.
新知探究
知识点2 负数的幂的正负与指数的关系
用计算器按下列顺序计算:
按键顺序 显示
-64
16
(
(-)
4
)
x3
=
(
(-)
2
)
=
4
新知探究
新知探究
把下列相同因数的乘积写成幂的形式,并说出底数和指数:
(1) (-6)×(-6) ×(-6)
底数是 –6,指数是 3
(2)
底数是
,指数是 4
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
知识点2 负数的幂的正负与指数的关系
新知探究
(3)在1210中,12是 数,10是___数,
读作 ;
(4) 的底数是 ,指数是 ,读作
;
7
底
指
12的10次方
的7次方
知识点2 负数的幂的正负与指数的关系
新知探究
乘方运算实际上就是乘法运算,根据有理数的乘法法则,可得乘方运算的法则:
求非 0 有理数的乘方,将其绝对值乘方,并取符号:正数的任意次幂都取正号;负数的奇次幂取负号,负数的偶次幂取正号.
新知探究
交 流
拉面师傅制作拉面时,按对折、拉伸的步骤,重复多次.
(1)先用乘法计算拉 12 次得到的面条数,再改用计算器计算幂,这两种方法哪种算得快?
用计算器计算幂算得快
212 = 4096
新知探究
(2)如果拉面师傅每次拉伸面条的长度为 0.8 m,那么拉 12 次后,得到的面条总长是多少米?
0.8×212 = 3276.8 (m)
随堂练习
2. 填空:
(1)在 74 中,底数是_____,指数是_____;
(2)在 中,底数是_____,指数是_____.
7
4
5
【教材P44 练习 第2题】
随堂练习
3. 计算:
(1)(-1.5)2; (2)4×(-2)3;
(3)-(-2)4; (4)(-2)3×(-2)2.
2.25
-32
-16
-32
【教材P44 练习 第3题】
课堂小结
根据有理数的乘法法则可以得出:
1.负数的奇次幂是负数,负数的偶次幂是正数;
2. 正数的任何次幂都是正数;
3. 0的任何正整数次幂都是0.
一般地,n个相同的乘数a相乘,记作 an,读作“a的n次方”.
求n个相同乘数的积的运算,叫作乘方,乘方的结果叫作幂.
乘方
沪科版数学七年级上册
第1章 有理数
第二课时 有理数的混合运算
1.6 有理数的乘方
学习目标
1.知道有理数加、减、乘、除、乘方混合运算的运算顺序.
2.会进行有理数的混合运算.
新知探究
在进行有理数的加、减、乘、除以及乘方混合运算时,一般应按下列顺序进行:
先乘方,再乘除,后加减;如果有括号,先进行括号里的运算.
知识点 有理数的混合运算
新知探究
例1 计算:
(1)-10 + 8÷(-2)2-(-4)×(-3);
解 (1) -10 + 8÷(-2)2-(-4)×(-3)
= -10 + 8÷4-4×3
= -10 + 2-12
= -20
知识点 有理数的混合运算
知识点 有理数的混合运算
(2) .
新知探究
随堂练习
1. 计算:
(1)-23-3×(-1)3-(-1)4;
解 -23-3×(-1)3-(-1)4
= -8-3×(-1)-1
= - 8 + 3 - 1
= - 6
【教材P45 练习 第1题】
(2) .
随堂练习
2. 计算:
(1) ;
解
【教材P45 练习 第2题】
随堂练习
沪科版数学七年级上册
第1章 有理数
第三课时 科学记数法
1.6 有理数的乘方
学习目标
1.了解科学记数法的现实意义,学会用科学记数法表示较大的数.
2.会用科学记数法表示的数进行简单的运算.
课堂导入
在日常生活中,常会接触到一些比较大的数,如长江三峡水库容量达 39 300 000 000 m3,光在空气中传播的速度大约是 300 000 000 m/s.
(1)长江三峡水库
(2)光的传播
课堂导入
39 300 000 000 300 000 000
这些较大的数,按上面的写法,写起来既麻烦又容易出错. 于是我们常用更大的数量级来表示,如将 39 300 000 000 表示为 393 亿.
你还知道其他的表示方法吗?
新知探究
10的乘方有如下的特点:
一般地,10的n次幂等于10···0(在1的后面有n个0),所以就可以用10的幂来表示一些大数.
你知道101,102,103,104分别等于多少吗?
的意义和规律是什么?
知识点 用科学记数法表示数
新知探究
书写简短,便于读数.
读作:5.67 乘 10 的8次方(幂)
例如:567 000 000
6 100 000 000 = 6.1×1 000 000 000
= 6.1×109
= 5.67×100 000 000
=5.67×
22 600 000 000 = 2.26×10 000 000 000
= 2.26×
知识点 用科学记数法表示数
新知探究
一般地,绝对值大于 10 的数都可记成 ±a×10n 的形式,其中 1≤a<10,n等于原数的整数位数减1. 这种记数方法,在科学技术方面是常用的,习惯上称之为科学记数法.
知识点 用科学记数法表示数
例1《2020 年全球森林资源评估》报告指出:1990 年以来,全球因砍伐而丧失了约 4.2 亿公顷森林,但森林丧失的速度已大幅下降,2015 至 2020 年,每年因砍伐而丧失的森林面积约为 1 000 万公顷. 请用科学记数法表示 4.2 亿 和 1 000 万,并用计算器表示.
解 4.2 亿 = 420 000 000 = 4.2×108.
1 000 万= 10 000 000 = 1×107.
知识点 用科学记数法表示数
新知探究
试一试 用科学记数法表示下列各数:
1×106.
-1.23×1011.
1 000 000,57 000 000,-123 000 000 000.
解:
1 000 000 =
-123 000 000 000 =
5.7×107.
57 000 000 =
知识点 用科学记数法表示数
新知探究
新知探究
5.7×107.
-1.23×1011.
57 000 000 =
-123 000 000 000 =
思考:
等号左边整数的位数与右边10的指数有什么关系?
用科学记数法表示一个n 位整数时,10的指数是 .
知识点 用科学记数法表示数
知识点 用科学记数法表示数
例2 下列各数是否用科学记数法表示的?为什么?
不是
2 400 000
2 400 000
3 100 000
3 100 000
不是
新知探究
随堂练习
1. 用科学记数法表示下列各数:
10 000,800 000,56 000 000,7 400 000.
解 10 000 = 1×104
800 000 = 8×105
56 000 000 = 5.6×107
7 400 000 = 7.4×106
【教材P46 练习 第1题】
2. 下列用科学记数法表示的数原来分别是什么数?
1×107,4×103,8.5×106,7.04×105.
解 1×107 = 10 000 000
4×103 = 4 000
8.5×106 =8 500 000
7.04×105 = 704 000
【教材P46 练习 第2题】
随堂练习
3. 截至 2022 年 12 月 31日,中国共产党党员总数为 9804.1 万名,用科学记数法表示 9804.1 万.
解 9804.1 万 = 98 041 000 = 9.8041×107
【教材P46 练习 第3题】
随堂练习
4. 从 2012 年到 2021 年,我国国内生产总值从 54 万亿元增长到 114 万亿元. 试用科学记数法表示 54 万亿和 114 万亿.
54 万亿 = 54 000 000 000 000 = 5.4×1013
114 万亿 = 114 000 000 000 000 = 1.14×1014
【教材P46 练习 第4题】
课堂小结
用科学记数法表示一个n位整数(n ≥2),其中10的指数是n-1.
科学记数法
把一个大于10的数表示成 a×10n 的形式(其中a 大于或等于1,且a 小于10,n是正整数),这种记法是科学记数法.
谢谢观看
Thank you
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
