沪科版九年级数学上册试题 相似形--折叠问题 同步练习 (含详解)
文档属性
| 名称 | 沪科版九年级数学上册试题 相似形--折叠问题 同步练习 (含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 11:57:22 | ||
图片预览



文档简介
《相似形--折叠问题》
一、单选题
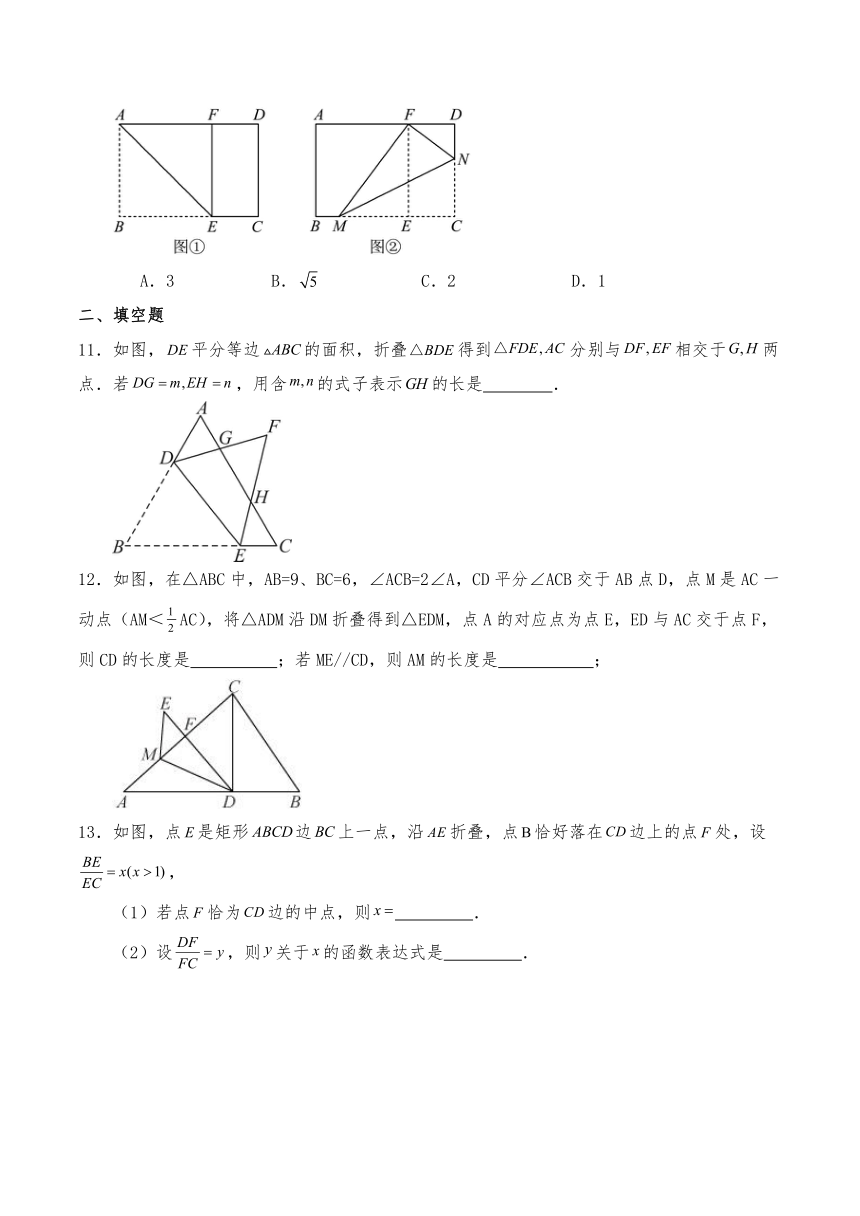
1.如图,在平面直角坐标系中,矩形的顶点B的坐标为,D为的中点,E是上一动点,将四边形沿折叠,使点A落在F处,点O落在G处,当线段的延长线恰好经过的中点H时,点F的坐标为( )
A. B. C. D.
2.如图,矩形中,,把它折叠起来,使顶点A与C重合,则折痕的长度为( )
A. B. C. D.
3.如图,矩形纸片,,点,分别在,上,把纸片如图沿折叠,点,的对应点分别为,,连接并延长交线段于点,则的值为( )
A. B. C. D.
4.如图,在正方形中,,E是的中点,F是延长线上的点,将沿折叠得到.连接并延长分别交、于O、H两点,若,则的长度为( )
A. B. C. D.
5.如图是一张矩形纸片,点是中点,点在上,把该纸片沿折叠,点、的对应点分别为、,与相交于点,的延长线经过点.若,则的值为( )
A. B. C. D.
6.如图,将矩形ABCD折叠,使点D落在AB上点D′处,折痕为AE;再次折叠,使点C落在ED′上点C′处,连接FC′并延长交AE于点G.若AB=8,AD=5,则FG长为( )
A. B. C. D.4
7.如图,矩形纸片ABCD,点E在边AD上,连接BE,点F在线段BE上,且,折叠矩形纸片使点C恰好落在点F处,折痕为DG,若,则折痕DG的长为( )
A. B. C. D.
8.如图,已知,,,点E为射线上一个动点,连接,将沿折叠,点B落在点处,过点作的垂线,分别交,于M,N两点,当为线段的三等分点时,的长为( )
A. B. C.或 D.或
9.如图,在等腰中,,.点和点分别是边和边上两点,连接.将沿折叠,得到,点恰好落在的中点处设与交于点,则( )
A. B. C. D.
10.在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
第一步:将矩形纸片的一端,利用图①的方法折出一个正方形,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕,如图②.
根据以上的操作,若,,则线段的长是( )
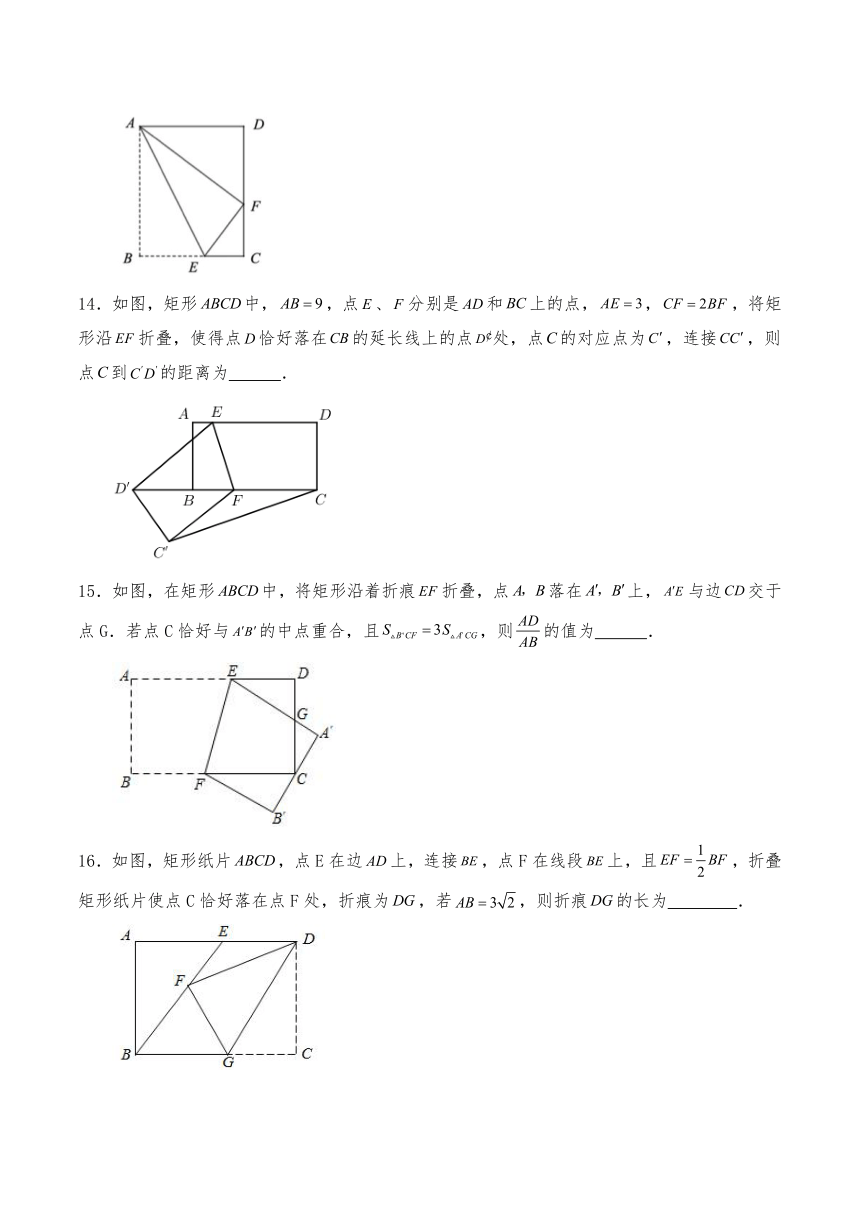
A.3 B. C.2 D.1
二、填空题
11.如图,平分等边的面积,折叠得到分别与相交于两点.若,用含的式子表示的长是 .
12.如图,在△ABC中,AB=9、BC=6,∠ACB=2∠A,CD平分∠ACB交于AB点D,点M是AC一动点(AM<AC),将△ADM沿DM折叠得到△EDM,点A的对应点为点E,ED与AC交于点F,则CD的长度是 ;若ME//CD,则AM的长度是 ;
13.如图,点是矩形边上一点,沿折叠,点恰好落在边上的点处,设,
(1)若点恰为边的中点,则 .
(2)设,则关于的函数表达式是 .
14.如图,矩形中,,点、分别是和上的点,,,将矩形沿折叠,使得点恰好落在的延长线上的点处,点的对应点为,连接,则点到的距离为 .
15.如图,在矩形中,将矩形沿着折痕折叠,点落在上,与边交于点G.若点C恰好与的中点重合,且,则的值为 .
16.如图,矩形纸片,点E在边上,连接,点F在线段上,且,折叠矩形纸片使点C恰好落在点F处,折痕为,若,则折痕的长为 .
17.如图是一张四边形纸片,,,,,点M,N分别是,上的点,将沿直线翻折,将沿直线翻折,点A和点B落在同一点G处,再将纸片沿直线折叠,点C恰好落在点D处,则的长为 .
18.若一个三角形三边长的比为,则称这个三角形为“345三角形”.如图,在矩形中,,点在边上.将沿折叠,得到,再将沿过点的直线折叠,使边与重合,点的对应点为,折痕为.若是“345三角形”,则的长为 .
三、解答题
19.问题情境:在数学活动课上,老师出了这样一道题:
在矩形中,,,将矩形绕着点顺时针旋转到矩形的位置,点D恰好在边CG上.
问题解决:
(1)如图1,连接AC,CF,AF,AF与CG交于点H.
①的值为______,______.
②求GH的长.
如图2,若将四边形沿渞直线CP折叠,得到四边形,使得点B的对应点恰好在EF上,点A的对应点为,点G在上,求AP的长.
20.综合与实践
问题情境:综合与实践课上,老师让同学们以“矩形纸片的折叠”为主题开展数学活动.矩形纸片中,,.
操作探究:如图1,将矩形纸片沿过点A的直线折叠,使点D的对应点落在边上,展开后折痕交于点E.
(1)的度数为______.
(2)求线段的长度.
拓展延伸:
如图2,在图1的基础上,继续沿过点A的直线折叠,使点B的对应点落在上,展开后折痕交于点F,连接.请判断的形状并说明理由.
21.如图,矩形中,P为上一点,且,连接,把矩形沿着折叠,点B落到,延长交延长线于Q,已知.
(1)若,求.
(2)若,求.
22.如图1将矩形分别沿过点的直线折叠,使点分别落在上的点E处和上的点H处,折痕为;
(1)求证:;
(2)若,,
①求;
②如图2,延长交于M点,求的长.
23.已知:菱形中,,,与交于点,点为上一点.
(1)求的长;
(2)若,求证:;
(3)若点在线段上不与、重合,以为对称轴,折叠,使点的对应点恰好落在菱形的边上,画出图形并求的长.
24.在数学活动课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作推断
如图1,点P是正方形纸片的边的中点,沿折叠,使点A落在点M处,延长交于点 F,连接. 则 .
(2)迁移探究
小华在(1)的条件下,继续探究:如图2,延长交于点E,连接.
① ;
②小华用大小不同的正方形纸片重复几次以上操作,总发现,请判断该发现是否正确?并说明理由.
(3)拓展应用
将边长为1的两个相同正方形拼成矩形,如图3,点P是上一动点,沿折叠,使点A落在点M处,射线交射线于点 F.当时,直接写出的长.
答案
一、单选题
1.A
【分析】连接,根据勾股定理得到,延长交的延长线于,根据三角形中位线定理得到,,根据平行四边形的性质得到,,根据折叠的性质得到,,求得,过作于,根据相似三角形的判定和性质定理即可得到结论.
解:连接,
矩形的顶点的坐标为,
,,
,
延长交的延长线于,
为的中点,为的中点,
,,
,
四边形是平行四边形,
,,
,
,,
将四边形沿折叠,使点落在处,点落在处,
,,
,,
,
,
,,
,
过作于,
,
,
,
,
,,
,.
故选:A.
2.A
【分析】由折叠的性质可知,,,再由矩形的性质得到,,证明得到,利用勾股定理求出,则,证明,得到,由此代入对应的值求解即可.
解:由折叠的性质可知,,,
∵四边形是矩形,
∴,,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
故选A.
3.A
【分析】根据折叠性质则可得出是的垂直平分线,则由直角三角形性质及矩形性质可得∠AEO=∠AGD,∠FHE=∠D=90°,根据相似三角形判定推出△EFH∽△GAD,再利用矩形判定及性质证得FH=AB,即可求得结果.
解:如图,过点F作FH⊥AD于点H,
∵点,的对应点分别为,,
∴,,
∴EF是AA'的垂直平分线.
∴∠AOE=90°.
∵四边形是矩形,
∴∠BAD=∠B=∠D=90°.
∴∠OAE+∠AEO=∠OAE+∠AGD,
∴∠AEO=∠AGD.
∵FH⊥AD,
∴∠FHE=∠D=90°.
∴△EFH∽△GAD.
∴.
∵∠AHF=∠BAD=∠B=90°,
∴四边形ABFH是矩形.
∴FH=AB.
∴;
故选:A.
4.A
【分析】解:设,则,由翻折可知,,易证根据相似的性质得解得及,勾股定理求出,再证得即可求解.
解:设,则,
由翻折可知,
,
,E是的中点,
,
由题意可知:
,
,
,
即,
解得,
,
,
又,
,
,
,
,
即:,
解得:,
故选:A.
5.C
【分析】过点E作于点H,令,,,则,,易证,得出,进而得出,则,根据勾股定理得出,最后求出的值.
解:过点E作于点H,
∵四边形为矩形,
∴,,
∴四边形和四边形为矩形,
∴,,
∵,
∴令,,,则,,
∵为的中点,
∴,
由对折可得:,而,
∴,
∴,
∴,
∴,
由题意,得,
又为公共角,
∴,
∴,
则,
整理,得,
解得(舍去),,
∴,,,
在中,
则,
解得,(负根舍去),
∴,
∴.
故选:C.
6.C
【分析】过点G作GI⊥AB,GH⊥ED',垂足分别为I、H,由折叠的性质可得C′E=5-4=1,在Rt△EFC′中,设FC′=x,则EF=3-x,由勾股定理得:12+(3-x)2=x2,解得:x=,再证明△BC′D'∽△C′GH,设C′H=3m,则GH=4m,C′G=5m,则HD'=GI=AI=4-3m,ID'=5-(4-3m)=1+3m=GH=4m,可得到C′G=5m=5,从而解决问题.
解:由折叠的性质得,∠AD'E=∠D=90°,AD=AD',
又∵∠DAB=90°,
∴四边形ADED'是矩形,
∵AD=AD',
∴四边形ADED'是正方形,
过点G作GI⊥AB,GH⊥ED',垂足分别为I、H,
∵AD'ED是正方形,
∴AD=DE=ED'=AD'=5,BC=BC′=5,∠C=∠BC′F=90°,FC=FC′,
∴D'B=EC=8-5=3,
在Rt△C′BD'中,C′D'=4,
∴C′E=5-4=1,
在Rt△EFC′中,设FC′=x,则EF=3-x,由勾股定理得:
12+(3-x)2=x2,
解得:x=,
∵∠BC′D'+∠GC′H=90°,∠GC′H+∠C′GH=90°,
∴∠BC′D'=∠C′GH,
又∵∠GHC′=∠BD'C′=90°,
∴△BC′D'∽△C′GH,
∴C′H:GH:C′G=BD':C′D':BC′=3:4:5,
设C′H=3m,则GH=4m,C′G=5m,
∴HD'=GI=AI=4-3m,ID'=5-(4-3m)=1+3m=GH=4m,
解得:m=1,
∴C′G=5m=5,
∴FG=;
故选:C.
7.C
【分析】过点作,垂足为点延长线交于点,由矩形的性质得,由平行线分线段成比例定理可得,得出的值,折叠的性质得,,在中,由勾股定理求得DM的值,由相似三角形的判定得出,相似三角形的性质得出的值,在中,由勾股定理求得DG的值.
解:如解图,过点作,垂足为点延长线交于点,
∵四边形是矩形,
,
∴四边形AMNB为矩形,
∴
.
由折叠性质可得,
.
,
,
,即
.
故选:C.
8.D
【分析】因为点为线段的三等分点,没有指明线段的占比情况,所以需要分两种情况讨论:①;② .然后由一线三垂直模型可证 ∽,再根据相似三角形的性质求得 的值,最后由 即可求得 的长.
解:当点为线段的三等分点时,需要分两种情况讨论:
①如图1,当时,
∵∥,, ,
∴四边形为矩形,
∴, , .
由折叠的性质可得,.
在中,.
∵, ,
∴,
∴∽,
∴,即 ,解得 ,
∴.
②如图2,当时,
∵∥,, ,
∴四边形为矩形,
∴, , .
由折叠的性质可得,.
在中,.
∵, ,
∴,
∴∽,
∴,即 ,解得,
∴.
综上所述,的长为或 .
故选:.
9.C
【解析】根据等腰直角三角形的性质得到AB=AC=4,∠A=∠B=45°,过B′作B′H⊥AB与H,得到AH=B′H=AB′,求得AH=B′H=1,由勾股定理得到BB′= ,由折叠的性质得到BF=,DE⊥BB′,根据相似三角形即可得到结论.
解:∵在等腰Rt△ABC中∠C=90°,AC=BC=2,
∴AB=AC=4,∠A=∠B=45°,
如图,过B′作B′H⊥AB与H,
∴△AHB′是等腰直角三角形,
∴AH=B′H=AB′,
∵AB′=,
∴AH=B′H=1,
∴BH=3,
∴BB′=,
∵将△BDE沿DE折叠,得到△B′DE,
∴BF=,DE⊥BB′,
∴∠BHB′=∠BFE=90°,
∵∠EBF=∠B′BH,
∴△BFE∽△BHB′,
∴,
∴,
∴EF=,
故答案为:
故选:C.
10.C
【分析】根据折叠的性质得:,,,设,则,利用勾股定理求出,再证明,得,求解即可.
解:如图,过点作,交于点,
在和中,
设,则,
,即:,
解得:,
,,
,
,
,
,
故选:C.
二、填空题
11.
【分析】先根据折叠的性质可得,,从而可得,再根据相似三角形的判定可证,根据相似三角形的性质可得,,然后将两个等式相加即可得.
解:是等边三角形,
,
∵折叠得到,
,
,,
平分等边的面积,
,
,
又,
,
,,
,
,
解得或(不符合题意,舍去),
故答案为:.
12. 5 2.5
【分析】(1)根据已知条件可得∠ACD=∠A=∠BCD,所以AD=CD,然后证明△ABC∽△CBD,进而可以解决问题;
(2)由翻折可得AM=EM,∠CAD=∠E,,由ME∥CD,可得∠E=∠EDC,DF//BC,且DF=CF,进而得到 ADF∽ ABC,求出DF、CF的长,再由AF:CF=AD:BD求出AF及MF的长, 再证明 MEF∽ CDF,最后求得AM的长.
解:(1)∵∠ACB=2∠A,CD平分∠ACB,
∴∠BCD=∠ACD=∠CAD,
∵∠B=∠B,
∴ BCD∽ BAC,
∴BC:AB=BD:BC,
即6:9=BD:6,BD=4,
∴AD=CD=9-4=5;
(2)∵△ADM沿DM折叠得到 EDM,
∴AM=EM,∠CAD=∠E,
∵ME//CD,
∴∠E=∠CDE,
∵∠BCD=∠ACD=∠CAD,
∴∠CDE=∠BCD=∠ACD,
∴DF//BC,且DF=CF,
∴ ADF∽ ABC,
∴DF:BC=AD:AB,
即DF:6=5:9,
解得DF=,
∴CF=;
∵DF//BC,
∴AF:CF=AD:BD,
即AF:=5:4,
解得:AF=,
设AM=ME=x,则MF=-x;
∵ME//CD,
∴ MEF∽ CDF,
∴ME:CD=MF:CF,
即x:5=(-x):,
解得x=2.5;
故答案:5; 2.5;
13. 2
【分析】(1)根据折叠和矩形的性质,证出AF = AB =CD,由点 B 恰好落在 CD 边上的中点 F 处,得出 DF =AF ,得 ∠DAF =30°,再求出∠CFE = ∠DAF =30°,即可得答案;
(2)先证△AFD∽△FEC,得,由AB=AF=CD,BE=EF,得,,由,,得=x-1,可得答案.
解:(1)由折叠,得 AF = AB , BE = EF ,
∵四边形 ABCD 是矩形,
∴ AB = CD , ∠D =90°,∠C =90°,
∵点 B 恰好落在 CD 边上的中点 F 处,
∴ DF =CD =AB = AF ,
在 Rt △ ADF 中,由 DF =AF ,得 ∠DAF =30°,
∵∠DAF + ∠AFD =90°,∠AFD + ∠CFE =90°,
∴∠CFE = ∠DAF =30°,
所以在 Rt △ ECF 中,,
∴,
∴x=2;
(2)∵△AFE是由△ABE折叠而来的,
∴△AFE≌△ABE,
∴BE=EF,AB=AF=CD,
∵∠EFC+∠AFD=90°,
∠EFC+∠FEC=90°,
∴∠AFD=∠FEC,
∵∠ADC=∠BCD,
∴△AFD∽△FEC,
∴ ,
∴,
∵AB=AF=CD,BE=EF,
∴,
∴,
∵,,
∴1+=x,
∴=x-1,
∴y=(x>1).
14.
【分析】作EG⊥BC于G点,作CH⊥交延长线于H点,设,则,综合折叠与矩形的基本性质,在中运用勾股定理求解出的值,从而得到,,然后判断出,利用相似三角形的性质求出CH的长度即可.
解:如图所示,作EG⊥BC于G点,作CH⊥交延长线于H点,
则点到的距离即为CH的长度,
∵,
∴设,则,
∴,,
由折叠的性质可知,,,
∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
又∵EG=AB=CD=,,
∴,
∴,
在中,由勾股定理得:,
解得:或(舍去),
∴,
在中,,
∴,
∵,,
∴,
∴,
∴,
即:,
解得:,
经检验,是上述方程的解,
故答案为:.
15.
【分析】首先得出,再根据翻折的性质得出,得出,最后利用勾股定理得出结果.
解:∵点C恰好与的中点重合,
∴,
由翻折的性质得,
∵,
∴,
∴,
又∵,
∴
设,
∴,
在Rt 中,
CF=,
∴AD=BC=BF+FC=,AB==2a,
∴,
故答案为:.
16.
【分析】过点作,垂足为点延长线交于点,由矩形的性质得,由平行线分线段成比例定理可得,得出的值,折叠的性质得,,在中,由勾股定理求得DM的值,由相似三角形的判定得出,相似三角形的性质得出的值,在中,由勾股定理求得DG的值.
解:如解图,过点作,垂足为点延长线交于点,
∵四边形是矩形,
,
∴四边形AMNB为矩形,
∴
.
由折叠性质可得,
.
,
,
,即
.
故答案为:
17.17
【分析】首先根据平行线的性质可得,再根据翻折的性质,可得,,,,,,,GD=8cm,设,则GN=acm,DN=(8+a)cm,再由折叠的性质可得,
可求得,据此即可求得a的值,即可求得BC的长.
解:
沿直线翻折后得到,沿直线翻折后得到
,,,,,
设cm
则cm
、G、N三点共线
cm
由对折知,
且
得,解得
故
故答案为:17
18.或
【分析】由折叠的性质,易得,分或两种情况进行讨论求解.
解:由折叠的性质可知,
,,.
∴,
∵,
∴,
∴.
∵是“345三角形”,
∴或.
①若,设,则,,
∴,
∴.
∴,解得,
∴.
在中,由勾股定理,得.
②若,同理,可得.
综上所述,的长为或.
三、解答题
19.
解:(1)①由题意可得旋转后得到,是旋转角,故
∵在矩形中,∠B=900,,
∴在中,
是由旋转得到
,
故答案为:;
②∵
∴,
∴,即,
解得.
(2)如图,连接
∵,
∴
∵
∴.
在中,
在中,
设,则
∴,,
在中,
∴
解得
∴
20.
解:(1)∵由题意可得,
∵矩形纸片中,,
∴
∴
∴,
故答案为:45°;
(2)∵矩形纸片中,
∴
∵,
∴
∵
∴
∴
∴
∴;
(3)∵
∴
由折叠的性质可得,,
∴
又∵
∴
∴,即
∴
∴
∴,即
又∵
∴
又∵
∴
∴,
∵
∴
∴
∴是等腰直角三角形.
21.
解:(1)设,
∵沿着折叠,点B落到,,.
∴,,
∵,
∴,
∴,
∴,
解得,
根据勾股定理,得,
∴,
解得(舍去)
∴.
(2)设,则,
∵,矩形,
∴,
∵
∴,
∴,
∴
∴,即,
∴,
∴,
∵,
∴.
设,
∵沿着折叠,点B落到,,.
∴,,
∵,
∴,
∴,
∴,
解得,
根据勾股定理,得,
∴,
解得(舍去)
∴.
22.
(1)解:如图:
∵是由折叠得到的 ,
∴,
∴,
又∵,
∴,
又∵,
∴;
(2)解:①∵,,
∴,,
∴ ,
∴ ,
又∵,
∴,即,
∴,;
②过M作于N,
由折叠知,
∴,
∴是等腰直角三角形,
∴,
∵,,
∴,
∴ ,
∴,
设,则,
∴,
∴, ,
∴.
23.
(1)解:∵是菱形,,
∵
∴
∴
(2)∵,,
∴,,
∴,
∴,
∴,
∴即,
∴,
∵,
∴;
(3)如图,当点在边上时,当点在边上时,延长交于,
由折叠知,则
由(2)可知
∴
如图,当点落在边上时,
由折叠可知
∴
∵,
∴
∵
∴
∴
∴
∴
∴的长为或,的长为或.
24.
(1)解:∵四边形是正方形,
∴,
∵点P是正方形纸片的边的中点,
∴,
∵沿折叠,使点A落在点M处,
∴,
∴,
∵,
∴,
∴,
∴,
∴.
故答案为:90.
(2)解:①∵四边形是正方形,
∴,
∵点P是正方形纸片的边的中点,
∴,
∵沿折叠,使点A落在点M处,
∴,
∴,
∵,
∴,
∴,
∴.
故答案为:45;
②判断正确,理由如下:
∵,
∴,
∵,
∴,
∴,
∴,
∴,即.
(3)解:∵将边长为1的两个相同正方形拼成矩形,
∴,
∴,
∵沿折叠,使点A落在点M处,
∵,
①当点F在的延长线上时,
∴,
设与交于E,
∵,
∴,
∴,
∴,解得:,
∴,
∵,
∴,
∴,即,解得: ,
∴.
②当点F在上时,
∵,
∴,
∴,
∴,解得:,
∴,
∴
∵,
∴,
∴,
∵沿折叠,使点A落在点M处,
∵,
∴,解得:.
∴.
一、单选题
1.如图,在平面直角坐标系中,矩形的顶点B的坐标为,D为的中点,E是上一动点,将四边形沿折叠,使点A落在F处,点O落在G处,当线段的延长线恰好经过的中点H时,点F的坐标为( )
A. B. C. D.
2.如图,矩形中,,把它折叠起来,使顶点A与C重合,则折痕的长度为( )
A. B. C. D.
3.如图,矩形纸片,,点,分别在,上,把纸片如图沿折叠,点,的对应点分别为,,连接并延长交线段于点,则的值为( )
A. B. C. D.
4.如图,在正方形中,,E是的中点,F是延长线上的点,将沿折叠得到.连接并延长分别交、于O、H两点,若,则的长度为( )
A. B. C. D.
5.如图是一张矩形纸片,点是中点,点在上,把该纸片沿折叠,点、的对应点分别为、,与相交于点,的延长线经过点.若,则的值为( )
A. B. C. D.
6.如图,将矩形ABCD折叠,使点D落在AB上点D′处,折痕为AE;再次折叠,使点C落在ED′上点C′处,连接FC′并延长交AE于点G.若AB=8,AD=5,则FG长为( )
A. B. C. D.4
7.如图,矩形纸片ABCD,点E在边AD上,连接BE,点F在线段BE上,且,折叠矩形纸片使点C恰好落在点F处,折痕为DG,若,则折痕DG的长为( )
A. B. C. D.
8.如图,已知,,,点E为射线上一个动点,连接,将沿折叠,点B落在点处,过点作的垂线,分别交,于M,N两点,当为线段的三等分点时,的长为( )
A. B. C.或 D.或
9.如图,在等腰中,,.点和点分别是边和边上两点,连接.将沿折叠,得到,点恰好落在的中点处设与交于点,则( )
A. B. C. D.
10.在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
第一步:将矩形纸片的一端,利用图①的方法折出一个正方形,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点C恰好落在点F处,得到折痕,如图②.
根据以上的操作,若,,则线段的长是( )
A.3 B. C.2 D.1
二、填空题
11.如图,平分等边的面积,折叠得到分别与相交于两点.若,用含的式子表示的长是 .
12.如图,在△ABC中,AB=9、BC=6,∠ACB=2∠A,CD平分∠ACB交于AB点D,点M是AC一动点(AM<AC),将△ADM沿DM折叠得到△EDM,点A的对应点为点E,ED与AC交于点F,则CD的长度是 ;若ME//CD,则AM的长度是 ;
13.如图,点是矩形边上一点,沿折叠,点恰好落在边上的点处,设,
(1)若点恰为边的中点,则 .
(2)设,则关于的函数表达式是 .
14.如图,矩形中,,点、分别是和上的点,,,将矩形沿折叠,使得点恰好落在的延长线上的点处,点的对应点为,连接,则点到的距离为 .
15.如图,在矩形中,将矩形沿着折痕折叠,点落在上,与边交于点G.若点C恰好与的中点重合,且,则的值为 .
16.如图,矩形纸片,点E在边上,连接,点F在线段上,且,折叠矩形纸片使点C恰好落在点F处,折痕为,若,则折痕的长为 .
17.如图是一张四边形纸片,,,,,点M,N分别是,上的点,将沿直线翻折,将沿直线翻折,点A和点B落在同一点G处,再将纸片沿直线折叠,点C恰好落在点D处,则的长为 .
18.若一个三角形三边长的比为,则称这个三角形为“345三角形”.如图,在矩形中,,点在边上.将沿折叠,得到,再将沿过点的直线折叠,使边与重合,点的对应点为,折痕为.若是“345三角形”,则的长为 .
三、解答题
19.问题情境:在数学活动课上,老师出了这样一道题:
在矩形中,,,将矩形绕着点顺时针旋转到矩形的位置,点D恰好在边CG上.
问题解决:
(1)如图1,连接AC,CF,AF,AF与CG交于点H.
①的值为______,______.
②求GH的长.
如图2,若将四边形沿渞直线CP折叠,得到四边形,使得点B的对应点恰好在EF上,点A的对应点为,点G在上,求AP的长.
20.综合与实践
问题情境:综合与实践课上,老师让同学们以“矩形纸片的折叠”为主题开展数学活动.矩形纸片中,,.
操作探究:如图1,将矩形纸片沿过点A的直线折叠,使点D的对应点落在边上,展开后折痕交于点E.
(1)的度数为______.
(2)求线段的长度.
拓展延伸:
如图2,在图1的基础上,继续沿过点A的直线折叠,使点B的对应点落在上,展开后折痕交于点F,连接.请判断的形状并说明理由.
21.如图,矩形中,P为上一点,且,连接,把矩形沿着折叠,点B落到,延长交延长线于Q,已知.
(1)若,求.
(2)若,求.
22.如图1将矩形分别沿过点的直线折叠,使点分别落在上的点E处和上的点H处,折痕为;
(1)求证:;
(2)若,,
①求;
②如图2,延长交于M点,求的长.
23.已知:菱形中,,,与交于点,点为上一点.
(1)求的长;
(2)若,求证:;
(3)若点在线段上不与、重合,以为对称轴,折叠,使点的对应点恰好落在菱形的边上,画出图形并求的长.
24.在数学活动课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作推断
如图1,点P是正方形纸片的边的中点,沿折叠,使点A落在点M处,延长交于点 F,连接. 则 .
(2)迁移探究
小华在(1)的条件下,继续探究:如图2,延长交于点E,连接.
① ;
②小华用大小不同的正方形纸片重复几次以上操作,总发现,请判断该发现是否正确?并说明理由.
(3)拓展应用
将边长为1的两个相同正方形拼成矩形,如图3,点P是上一动点,沿折叠,使点A落在点M处,射线交射线于点 F.当时,直接写出的长.
答案
一、单选题
1.A
【分析】连接,根据勾股定理得到,延长交的延长线于,根据三角形中位线定理得到,,根据平行四边形的性质得到,,根据折叠的性质得到,,求得,过作于,根据相似三角形的判定和性质定理即可得到结论.
解:连接,
矩形的顶点的坐标为,
,,
,
延长交的延长线于,
为的中点,为的中点,
,,
,
四边形是平行四边形,
,,
,
,,
将四边形沿折叠,使点落在处,点落在处,
,,
,,
,
,
,,
,
过作于,
,
,
,
,
,,
,.
故选:A.
2.A
【分析】由折叠的性质可知,,,再由矩形的性质得到,,证明得到,利用勾股定理求出,则,证明,得到,由此代入对应的值求解即可.
解:由折叠的性质可知,,,
∵四边形是矩形,
∴,,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
故选A.
3.A
【分析】根据折叠性质则可得出是的垂直平分线,则由直角三角形性质及矩形性质可得∠AEO=∠AGD,∠FHE=∠D=90°,根据相似三角形判定推出△EFH∽△GAD,再利用矩形判定及性质证得FH=AB,即可求得结果.
解:如图,过点F作FH⊥AD于点H,
∵点,的对应点分别为,,
∴,,
∴EF是AA'的垂直平分线.
∴∠AOE=90°.
∵四边形是矩形,
∴∠BAD=∠B=∠D=90°.
∴∠OAE+∠AEO=∠OAE+∠AGD,
∴∠AEO=∠AGD.
∵FH⊥AD,
∴∠FHE=∠D=90°.
∴△EFH∽△GAD.
∴.
∵∠AHF=∠BAD=∠B=90°,
∴四边形ABFH是矩形.
∴FH=AB.
∴;
故选:A.
4.A
【分析】解:设,则,由翻折可知,,易证根据相似的性质得解得及,勾股定理求出,再证得即可求解.
解:设,则,
由翻折可知,
,
,E是的中点,
,
由题意可知:
,
,
,
即,
解得,
,
,
又,
,
,
,
,
即:,
解得:,
故选:A.
5.C
【分析】过点E作于点H,令,,,则,,易证,得出,进而得出,则,根据勾股定理得出,最后求出的值.
解:过点E作于点H,
∵四边形为矩形,
∴,,
∴四边形和四边形为矩形,
∴,,
∵,
∴令,,,则,,
∵为的中点,
∴,
由对折可得:,而,
∴,
∴,
∴,
∴,
由题意,得,
又为公共角,
∴,
∴,
则,
整理,得,
解得(舍去),,
∴,,,
在中,
则,
解得,(负根舍去),
∴,
∴.
故选:C.
6.C
【分析】过点G作GI⊥AB,GH⊥ED',垂足分别为I、H,由折叠的性质可得C′E=5-4=1,在Rt△EFC′中,设FC′=x,则EF=3-x,由勾股定理得:12+(3-x)2=x2,解得:x=,再证明△BC′D'∽△C′GH,设C′H=3m,则GH=4m,C′G=5m,则HD'=GI=AI=4-3m,ID'=5-(4-3m)=1+3m=GH=4m,可得到C′G=5m=5,从而解决问题.
解:由折叠的性质得,∠AD'E=∠D=90°,AD=AD',
又∵∠DAB=90°,
∴四边形ADED'是矩形,
∵AD=AD',
∴四边形ADED'是正方形,
过点G作GI⊥AB,GH⊥ED',垂足分别为I、H,
∵AD'ED是正方形,
∴AD=DE=ED'=AD'=5,BC=BC′=5,∠C=∠BC′F=90°,FC=FC′,
∴D'B=EC=8-5=3,
在Rt△C′BD'中,C′D'=4,
∴C′E=5-4=1,
在Rt△EFC′中,设FC′=x,则EF=3-x,由勾股定理得:
12+(3-x)2=x2,
解得:x=,
∵∠BC′D'+∠GC′H=90°,∠GC′H+∠C′GH=90°,
∴∠BC′D'=∠C′GH,
又∵∠GHC′=∠BD'C′=90°,
∴△BC′D'∽△C′GH,
∴C′H:GH:C′G=BD':C′D':BC′=3:4:5,
设C′H=3m,则GH=4m,C′G=5m,
∴HD'=GI=AI=4-3m,ID'=5-(4-3m)=1+3m=GH=4m,
解得:m=1,
∴C′G=5m=5,
∴FG=;
故选:C.
7.C
【分析】过点作,垂足为点延长线交于点,由矩形的性质得,由平行线分线段成比例定理可得,得出的值,折叠的性质得,,在中,由勾股定理求得DM的值,由相似三角形的判定得出,相似三角形的性质得出的值,在中,由勾股定理求得DG的值.
解:如解图,过点作,垂足为点延长线交于点,
∵四边形是矩形,
,
∴四边形AMNB为矩形,
∴
.
由折叠性质可得,
.
,
,
,即
.
故选:C.
8.D
【分析】因为点为线段的三等分点,没有指明线段的占比情况,所以需要分两种情况讨论:①;② .然后由一线三垂直模型可证 ∽,再根据相似三角形的性质求得 的值,最后由 即可求得 的长.
解:当点为线段的三等分点时,需要分两种情况讨论:
①如图1,当时,
∵∥,, ,
∴四边形为矩形,
∴, , .
由折叠的性质可得,.
在中,.
∵, ,
∴,
∴∽,
∴,即 ,解得 ,
∴.
②如图2,当时,
∵∥,, ,
∴四边形为矩形,
∴, , .
由折叠的性质可得,.
在中,.
∵, ,
∴,
∴∽,
∴,即 ,解得,
∴.
综上所述,的长为或 .
故选:.
9.C
【解析】根据等腰直角三角形的性质得到AB=AC=4,∠A=∠B=45°,过B′作B′H⊥AB与H,得到AH=B′H=AB′,求得AH=B′H=1,由勾股定理得到BB′= ,由折叠的性质得到BF=,DE⊥BB′,根据相似三角形即可得到结论.
解:∵在等腰Rt△ABC中∠C=90°,AC=BC=2,
∴AB=AC=4,∠A=∠B=45°,
如图,过B′作B′H⊥AB与H,
∴△AHB′是等腰直角三角形,
∴AH=B′H=AB′,
∵AB′=,
∴AH=B′H=1,
∴BH=3,
∴BB′=,
∵将△BDE沿DE折叠,得到△B′DE,
∴BF=,DE⊥BB′,
∴∠BHB′=∠BFE=90°,
∵∠EBF=∠B′BH,
∴△BFE∽△BHB′,
∴,
∴,
∴EF=,
故答案为:
故选:C.
10.C
【分析】根据折叠的性质得:,,,设,则,利用勾股定理求出,再证明,得,求解即可.
解:如图,过点作,交于点,
在和中,
设,则,
,即:,
解得:,
,,
,
,
,
,
故选:C.
二、填空题
11.
【分析】先根据折叠的性质可得,,从而可得,再根据相似三角形的判定可证,根据相似三角形的性质可得,,然后将两个等式相加即可得.
解:是等边三角形,
,
∵折叠得到,
,
,,
平分等边的面积,
,
,
又,
,
,,
,
,
解得或(不符合题意,舍去),
故答案为:.
12. 5 2.5
【分析】(1)根据已知条件可得∠ACD=∠A=∠BCD,所以AD=CD,然后证明△ABC∽△CBD,进而可以解决问题;
(2)由翻折可得AM=EM,∠CAD=∠E,,由ME∥CD,可得∠E=∠EDC,DF//BC,且DF=CF,进而得到 ADF∽ ABC,求出DF、CF的长,再由AF:CF=AD:BD求出AF及MF的长, 再证明 MEF∽ CDF,最后求得AM的长.
解:(1)∵∠ACB=2∠A,CD平分∠ACB,
∴∠BCD=∠ACD=∠CAD,
∵∠B=∠B,
∴ BCD∽ BAC,
∴BC:AB=BD:BC,
即6:9=BD:6,BD=4,
∴AD=CD=9-4=5;
(2)∵△ADM沿DM折叠得到 EDM,
∴AM=EM,∠CAD=∠E,
∵ME//CD,
∴∠E=∠CDE,
∵∠BCD=∠ACD=∠CAD,
∴∠CDE=∠BCD=∠ACD,
∴DF//BC,且DF=CF,
∴ ADF∽ ABC,
∴DF:BC=AD:AB,
即DF:6=5:9,
解得DF=,
∴CF=;
∵DF//BC,
∴AF:CF=AD:BD,
即AF:=5:4,
解得:AF=,
设AM=ME=x,则MF=-x;
∵ME//CD,
∴ MEF∽ CDF,
∴ME:CD=MF:CF,
即x:5=(-x):,
解得x=2.5;
故答案:5; 2.5;
13. 2
【分析】(1)根据折叠和矩形的性质,证出AF = AB =CD,由点 B 恰好落在 CD 边上的中点 F 处,得出 DF =AF ,得 ∠DAF =30°,再求出∠CFE = ∠DAF =30°,即可得答案;
(2)先证△AFD∽△FEC,得,由AB=AF=CD,BE=EF,得,,由,,得=x-1,可得答案.
解:(1)由折叠,得 AF = AB , BE = EF ,
∵四边形 ABCD 是矩形,
∴ AB = CD , ∠D =90°,∠C =90°,
∵点 B 恰好落在 CD 边上的中点 F 处,
∴ DF =CD =AB = AF ,
在 Rt △ ADF 中,由 DF =AF ,得 ∠DAF =30°,
∵∠DAF + ∠AFD =90°,∠AFD + ∠CFE =90°,
∴∠CFE = ∠DAF =30°,
所以在 Rt △ ECF 中,,
∴,
∴x=2;
(2)∵△AFE是由△ABE折叠而来的,
∴△AFE≌△ABE,
∴BE=EF,AB=AF=CD,
∵∠EFC+∠AFD=90°,
∠EFC+∠FEC=90°,
∴∠AFD=∠FEC,
∵∠ADC=∠BCD,
∴△AFD∽△FEC,
∴ ,
∴,
∵AB=AF=CD,BE=EF,
∴,
∴,
∵,,
∴1+=x,
∴=x-1,
∴y=(x>1).
14.
【分析】作EG⊥BC于G点,作CH⊥交延长线于H点,设,则,综合折叠与矩形的基本性质,在中运用勾股定理求解出的值,从而得到,,然后判断出,利用相似三角形的性质求出CH的长度即可.
解:如图所示,作EG⊥BC于G点,作CH⊥交延长线于H点,
则点到的距离即为CH的长度,
∵,
∴设,则,
∴,,
由折叠的性质可知,,,
∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
又∵EG=AB=CD=,,
∴,
∴,
在中,由勾股定理得:,
解得:或(舍去),
∴,
在中,,
∴,
∵,,
∴,
∴,
∴,
即:,
解得:,
经检验,是上述方程的解,
故答案为:.
15.
【分析】首先得出,再根据翻折的性质得出,得出,最后利用勾股定理得出结果.
解:∵点C恰好与的中点重合,
∴,
由翻折的性质得,
∵,
∴,
∴,
又∵,
∴
设,
∴,
在Rt 中,
CF=,
∴AD=BC=BF+FC=,AB==2a,
∴,
故答案为:.
16.
【分析】过点作,垂足为点延长线交于点,由矩形的性质得,由平行线分线段成比例定理可得,得出的值,折叠的性质得,,在中,由勾股定理求得DM的值,由相似三角形的判定得出,相似三角形的性质得出的值,在中,由勾股定理求得DG的值.
解:如解图,过点作,垂足为点延长线交于点,
∵四边形是矩形,
,
∴四边形AMNB为矩形,
∴
.
由折叠性质可得,
.
,
,
,即
.
故答案为:
17.17
【分析】首先根据平行线的性质可得,再根据翻折的性质,可得,,,,,,,GD=8cm,设,则GN=acm,DN=(8+a)cm,再由折叠的性质可得,
可求得,据此即可求得a的值,即可求得BC的长.
解:
沿直线翻折后得到,沿直线翻折后得到
,,,,,
设cm
则cm
、G、N三点共线
cm
由对折知,
且
得,解得
故
故答案为:17
18.或
【分析】由折叠的性质,易得,分或两种情况进行讨论求解.
解:由折叠的性质可知,
,,.
∴,
∵,
∴,
∴.
∵是“345三角形”,
∴或.
①若,设,则,,
∴,
∴.
∴,解得,
∴.
在中,由勾股定理,得.
②若,同理,可得.
综上所述,的长为或.
三、解答题
19.
解:(1)①由题意可得旋转后得到,是旋转角,故
∵在矩形中,∠B=900,,
∴在中,
是由旋转得到
,
故答案为:;
②∵
∴,
∴,即,
解得.
(2)如图,连接
∵,
∴
∵
∴.
在中,
在中,
设,则
∴,,
在中,
∴
解得
∴
20.
解:(1)∵由题意可得,
∵矩形纸片中,,
∴
∴
∴,
故答案为:45°;
(2)∵矩形纸片中,
∴
∵,
∴
∵
∴
∴
∴
∴;
(3)∵
∴
由折叠的性质可得,,
∴
又∵
∴
∴,即
∴
∴
∴,即
又∵
∴
又∵
∴
∴,
∵
∴
∴
∴是等腰直角三角形.
21.
解:(1)设,
∵沿着折叠,点B落到,,.
∴,,
∵,
∴,
∴,
∴,
解得,
根据勾股定理,得,
∴,
解得(舍去)
∴.
(2)设,则,
∵,矩形,
∴,
∵
∴,
∴,
∴
∴,即,
∴,
∴,
∵,
∴.
设,
∵沿着折叠,点B落到,,.
∴,,
∵,
∴,
∴,
∴,
解得,
根据勾股定理,得,
∴,
解得(舍去)
∴.
22.
(1)解:如图:
∵是由折叠得到的 ,
∴,
∴,
又∵,
∴,
又∵,
∴;
(2)解:①∵,,
∴,,
∴ ,
∴ ,
又∵,
∴,即,
∴,;
②过M作于N,
由折叠知,
∴,
∴是等腰直角三角形,
∴,
∵,,
∴,
∴ ,
∴,
设,则,
∴,
∴, ,
∴.
23.
(1)解:∵是菱形,,
∵
∴
∴
(2)∵,,
∴,,
∴,
∴,
∴,
∴即,
∴,
∵,
∴;
(3)如图,当点在边上时,当点在边上时,延长交于,
由折叠知,则
由(2)可知
∴
如图,当点落在边上时,
由折叠可知
∴
∵,
∴
∵
∴
∴
∴
∴
∴的长为或,的长为或.
24.
(1)解:∵四边形是正方形,
∴,
∵点P是正方形纸片的边的中点,
∴,
∵沿折叠,使点A落在点M处,
∴,
∴,
∵,
∴,
∴,
∴,
∴.
故答案为:90.
(2)解:①∵四边形是正方形,
∴,
∵点P是正方形纸片的边的中点,
∴,
∵沿折叠,使点A落在点M处,
∴,
∴,
∵,
∴,
∴,
∴.
故答案为:45;
②判断正确,理由如下:
∵,
∴,
∵,
∴,
∴,
∴,
∴,即.
(3)解:∵将边长为1的两个相同正方形拼成矩形,
∴,
∴,
∵沿折叠,使点A落在点M处,
∵,
①当点F在的延长线上时,
∴,
设与交于E,
∵,
∴,
∴,
∴,解得:,
∴,
∵,
∴,
∴,即,解得: ,
∴.
②当点F在上时,
∵,
∴,
∴,
∴,解得:,
∴,
∴
∵,
∴,
∴,
∵沿折叠,使点A落在点M处,
∵,
∴,解得:.
∴.
