沪科版九年级数学上册 第二十二章 相似形 单元检测卷 (含详解)
文档属性
| 名称 | 沪科版九年级数学上册 第二十二章 相似形 单元检测卷 (含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 863.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 11:58:25 | ||
图片预览



文档简介
第二十二章《相似形》单元检测卷
一、单选题(本大题共10小题,每小题3分,共30分)
1.若,则( )
A.6 B. C.1 D.
2.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段,则线段的长是( )
A. B.1 C. D.2
3.如图,将图形用放大镜放大,应该属于( ).
A.平移变换 B.相似变换 C.旋转变换 D.对称变换
4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC
C. D.
5.如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
A.18 B. C. D.
6.如图,为等边三角形,点,分别在边,上,,若,,则的长为( )
A. B. C. D.
7.如图,在中,,D、E分别为中点,连接相交于点F,点G在上,且,则四边形的面积为( )
A. B. C. D.
8.如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为( )
A. B. C. D.
9.如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A. B. C. D.
10.如图,ABC中,点D、E分别在AB、AC上,且,下列结论正确的是( )
A.DE:BC=1:2 B.ADE与ABC的面积比为1:3
C.ADE与ABC的周长比为1:2 D.DEBC
二、填空题(本大题共8小题,每小题4分,共32分)
11.如图,乐器上的一根弦,两个端点固定在乐器板面上,支撑点是靠近点的黄金分割点,支撑点是靠近点的黄金分割点,之间的距离为 .
12.如图,在中,点在边上,点在边上,请添加一个条件 ,使.
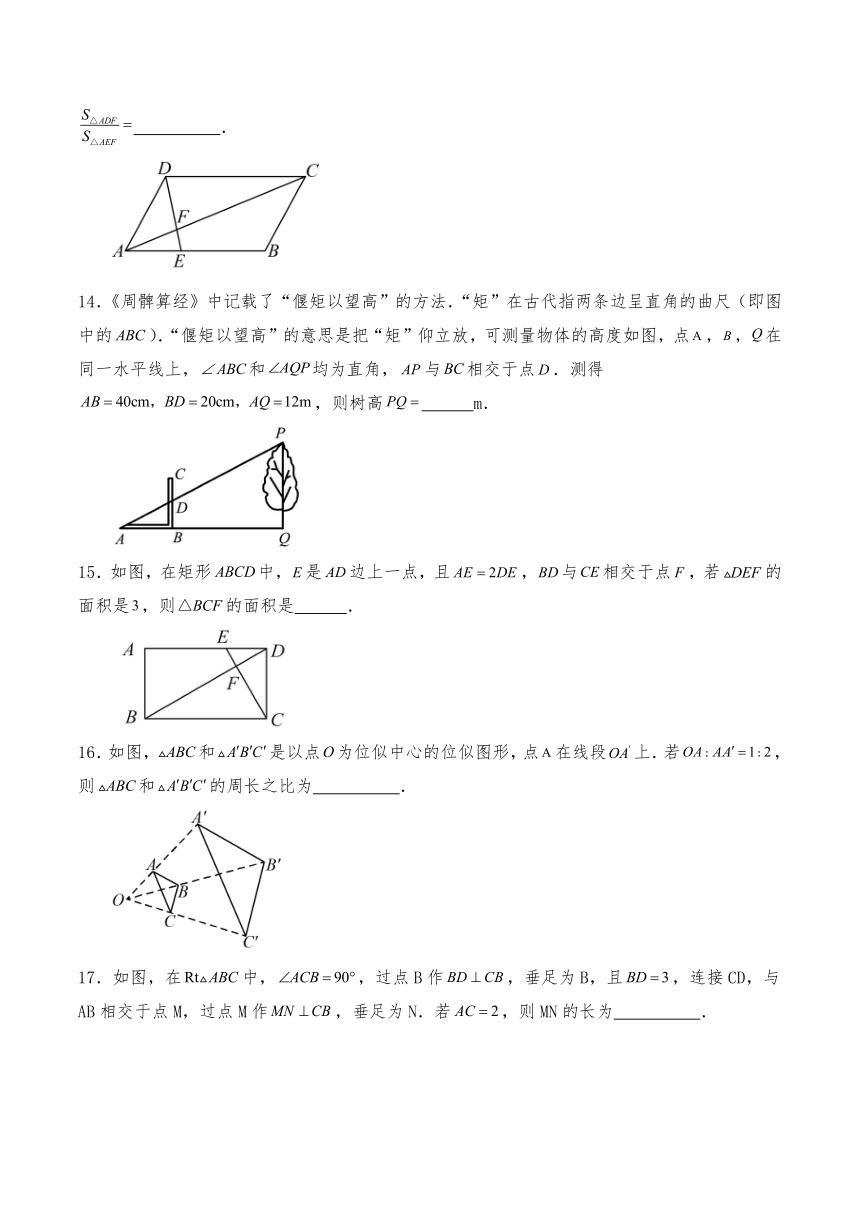
13.如图,在平行四边形中,E是线段上一点,连结交于点F.若,则 .
14.《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点,,在同一水平线上,和均为直角,与相交于点.测得,则树高 m.
15.如图,在矩形中,是边上一点,且,与相交于点,若的面积是,则的面积是 .
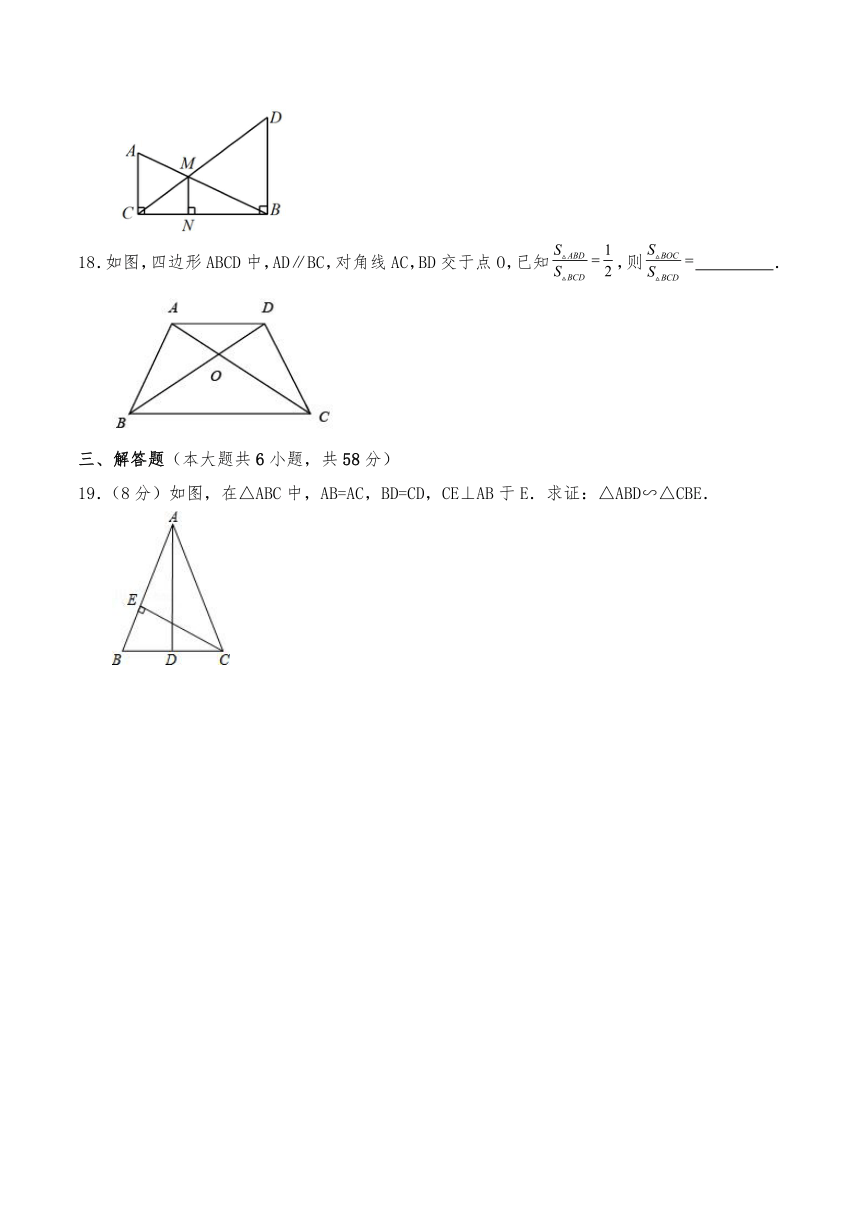
16.如图,和是以点为位似中心的位似图形,点在线段上.若,则和的周长之比为 .
17.如图,在中,,过点B作,垂足为B,且,连接CD,与AB相交于点M,过点M作,垂足为N.若,则MN的长为 .
18.如图,四边形ABCD中,AD∥BC,对角线AC,BD交于点O,已知,则 .
三、解答题(本大题共6小题,共58分)
19.(8分)如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
20.(8分)在中,是斜边上的高.
(1)证明:;
(2)若,求的长.
21.(10分)如图,四边形ABCD中,AB=AC=AD ,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.
(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
22.(10分)尺规作图(只保留作图痕迹,不要求写出作法),如图,已知ABC,且AB>AC.
(1)在AB边上求作点D,使DB=DC;
(2)在AC边上求作点E,使ADE∽ACB.
23.(10分)如图,在和中,,.
(1)求证:;
(2)若,,求的长.
24.(12分)如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥ AF于点H,分别交AC、CD于点G、P,连接GE、GF.
(1)求证:△ OAE ≌ △ OBG.
(2)试问:四边形BFGE是否为菱形 若是,请证明;若不是,请说明理由.
(3)试求:的值(结果保留根号).
答案
一、单选题
1.A
【分析】根据等式的性质即可得出结果.
解:等式两边乘以,得,
故选:A.
2.C
【分析】过点作五条平行横线的垂线,交第三、四条直线,分别于、,根据题意得,然后利用平行线分线段成比例定理即可求解.
解:过点作五条平行横线的垂线,交第三、四条直线,分别于、,
根据题意得,
∵,
∴,
又∵,
∴
故选:C
3.B
【分析】根据放大镜成像的特点,结合各变换的特点即可得出答案.
解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.
故选B.
4.D
解:A.当∠ABP=∠C时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
B.当∠APB=∠ABC时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
C.当时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
D.无法得到△ABP∽△ACB,故此选项正确.
故选:D.
5.B
解:先由四边形ABCD是正方形,AB=12,BM=5,可得MC=12﹣5=7,
根据两角对应相等的两三角形相似,得出△ABM∽△MCG,
根据相似三角形的性质得到,
故可得出CG=,再求出DG=12﹣=,
根据平行线的性质得出△MCG∽△EDG,即可得出,
即,
解得DE=.
故选B.
6.C
【分析】证明,根据题意得出,进而即可求解.
解:∵为等边三角形,
∴,
∵,,
∴,
∴
∴
∵,
∴,
∴
∵
∴,
故选:C.
7.B
【分析】连接,首先得到,,然后证明出,进而得到,然后利用三角形面积公式求出,最后利用求解即可.
解:如图所示,连接,
∵D、E分别为中点,
∴,,
∴,,,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∴.
故选:B.
8.B
【分析】根据镜面反射性质,可求出,再利用垂直求,最后根据三角形相似的性质,即可求出答案.
解:如图所示,
由图可知,,,
∠ABC=∠CDE=900.
根据镜面的反射性质,
∴,
∴,
,
,
.
小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,
,,.
.
.
故选:B.
9.C
【分析】根据平行线分线段成比例定理即可判断A,根据相似三角形的性质即可判断B、C、D.
解:∵,
∴,△DEF∽△CBF,△ADE∽△ABC,故A不符合题意;
∴,,故B不符合题意,C符合题意;
∴,故D不符合题意;
故选C.
10.D
【分析】根据相似三角形的判定与性质进行逐一判断即可.
解:∵,
∴AD:AB=AE:AC=1:3,
∵∠A=∠A,
∴△ADE∽△ABC,
∴DE:BC=1:3,故A错误;
∵△ADE∽△ABC,
∴△ADE与△ABC的面积比为1:9,周长的比为1:3,故B和C错误;
∵△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.故D正确.
故选:D.
二、填空题
11.
【分析】黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比.其比值是一个无理数,用分数表示为,由此即可求解.
解:弦,点是靠近点的黄金分割点,设,则,
∴,解方程得,,
点是靠近点的黄金分割点,设,则,
∴,解方程得,,
∴之间的距离为,
故答案为:.
12.∠ADE=∠B(答案不唯一).
【分析】已知有一个公共角,则可以再添加一个角从而利用有两组角对应相等的两个三角形相似来判定或添加夹此角的两边对应成比例也可以判定.
解:解∶∵∠A=∠A,
∴根据两角相等的两个三角形相似,可添加条件∠ADE=∠B或∠AED=∠C证相似;
根据两边对应成比例且夹角相等,可添加条件证相似.
故答案为∶∠ADE=∠B(答案不唯一).
13.
【分析】四边形是平行四边形,则,可证明,得到,由进一步即可得到答案.
解:∵四边形是平行四边形,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
故答案为:
14.
【分析】根据题意可得,然后相似三角形的性质,即可求解.
解:∵和均为直角
∴,
∴,
∴
∵,
∴,
故答案为:.
15.27
【分析】根据矩形的性质,很容易证明∽,相似三角形之比等于对应边比的平方,即可求出的面积.
解:四边形是矩形,
,
,
,
∽,
,,
::,
::,即::,
.
故答案为:.
16.
【分析】根据位似图形的性质即可求出答案.
解:,
,
设周长为,设周长为,
和是以点为位似中心的位似图形,
.
.
和的周长之比为.
故答案为:.
17.
【分析】根据MN⊥BC,AC⊥BC,DB⊥BC,得,可得,因为,列出关于MN的方程,即可求出MN的长.
解:∵MN⊥BC,DB⊥BC,
∴AC∥MN∥DB,
∴,
∴
即,
又∵,
∴,
解得,
故填:.
18.
【分析】先根据等高的两个三角形的面积比等于边长比,得出,再根据△AOD∽△COB得出,再根据等高的两个三角形的面积比等于边长比计算即可
解:作AE⊥BC,CF⊥BD
∵
∴△ABD和△BCD等高,高均为AE
∴
∵AD∥BC
∴△AOD∽△COB
∴
∵△BOC和△DOC等高,高均为CF
∴
∴
故答案为:
三、解答题
19.
解:∵在△ABC中,AB=AC,BD=CD,
∴AD⊥BC.
又∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
20.
解:(1)证明:∵是斜边上的高.
∴,
∴,
∴
又∵
∴,
(2)∵
∴,
又
∴.
21.
解:(1)∵AB=AD,AC平分∠BAD,
∴AC⊥BD,
∴∠ACD+∠BDC=90°,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠ADC+∠BDC=90°,
∴∠BDC=∠PDC;
(2)解:过点C作CM⊥PD于点M,
∵∠BDC=∠PDC,
∴CE=CM,
∵∠CMP=∠ADP=90°,∠P=∠P,
∴△CPM∽△APD,
∴,
设CM=CE=x,
∵CE:CP=2:3,
∴PC=x,
∵AB=AD=AC=1,
∴,
解得:x=,
故AE=1﹣=.
22.
解:(1)如图,点即为所求.
(2)如图,点即为所求.
23.
解:证明:(1),
,即,
在和中,,
;
(2)由(1)已证:,
,
,,
,
解得或(不符题意,舍去),
则的长为9.
24.
解:(1)证明:因为四边形是正方形, ∴OA=OB,∠AOE=∠BOG=90°.
∵BH⊥AF,
与中, ∠AOB=∠BOG,
OA=OB, ∴△OAE ≌△OBG(ASA).
∠OAE=∠OBG,
(2)四边形是菱形,理由如下:在△ AHG与△AHB中,
∠GAH=∠BAH,
HA=HA,
∠AHG=∠AHB=90°,
∴△AHG≌△AHB(ASA),
是线段的垂直平分线,∴ 四边形是菱形.
(3) 设 菱形的边长为.
∵ 四边形是菱形,
在Rt△GOE中,由勾股定理可得,∴AC=2a=(2+)b,
.
.
一、单选题(本大题共10小题,每小题3分,共30分)
1.若,则( )
A.6 B. C.1 D.
2.如图,五线谱是由等距离、等长度的五条平行横线组成的,同一条直线上的三个点A,B,C都在横线上.若线段,则线段的长是( )
A. B.1 C. D.2
3.如图,将图形用放大镜放大,应该属于( ).
A.平移变换 B.相似变换 C.旋转变换 D.对称变换
4.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
A.∠ABP=∠C B.∠APB=∠ABC
C. D.
5.如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为( )
A.18 B. C. D.
6.如图,为等边三角形,点,分别在边,上,,若,,则的长为( )
A. B. C. D.
7.如图,在中,,D、E分别为中点,连接相交于点F,点G在上,且,则四边形的面积为( )
A. B. C. D.
8.如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,则旗杆高度为( )
A. B. C. D.
9.如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A. B. C. D.
10.如图,ABC中,点D、E分别在AB、AC上,且,下列结论正确的是( )
A.DE:BC=1:2 B.ADE与ABC的面积比为1:3
C.ADE与ABC的周长比为1:2 D.DEBC
二、填空题(本大题共8小题,每小题4分,共32分)
11.如图,乐器上的一根弦,两个端点固定在乐器板面上,支撑点是靠近点的黄金分割点,支撑点是靠近点的黄金分割点,之间的距离为 .
12.如图,在中,点在边上,点在边上,请添加一个条件 ,使.
13.如图,在平行四边形中,E是线段上一点,连结交于点F.若,则 .
14.《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度如图,点,,在同一水平线上,和均为直角,与相交于点.测得,则树高 m.
15.如图,在矩形中,是边上一点,且,与相交于点,若的面积是,则的面积是 .
16.如图,和是以点为位似中心的位似图形,点在线段上.若,则和的周长之比为 .
17.如图,在中,,过点B作,垂足为B,且,连接CD,与AB相交于点M,过点M作,垂足为N.若,则MN的长为 .
18.如图,四边形ABCD中,AD∥BC,对角线AC,BD交于点O,已知,则 .
三、解答题(本大题共6小题,共58分)
19.(8分)如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
20.(8分)在中,是斜边上的高.
(1)证明:;
(2)若,求的长.
21.(10分)如图,四边形ABCD中,AB=AC=AD ,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.
(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
22.(10分)尺规作图(只保留作图痕迹,不要求写出作法),如图,已知ABC,且AB>AC.
(1)在AB边上求作点D,使DB=DC;
(2)在AC边上求作点E,使ADE∽ACB.
23.(10分)如图,在和中,,.
(1)求证:;
(2)若,,求的长.
24.(12分)如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥ AF于点H,分别交AC、CD于点G、P,连接GE、GF.
(1)求证:△ OAE ≌ △ OBG.
(2)试问:四边形BFGE是否为菱形 若是,请证明;若不是,请说明理由.
(3)试求:的值(结果保留根号).
答案
一、单选题
1.A
【分析】根据等式的性质即可得出结果.
解:等式两边乘以,得,
故选:A.
2.C
【分析】过点作五条平行横线的垂线,交第三、四条直线,分别于、,根据题意得,然后利用平行线分线段成比例定理即可求解.
解:过点作五条平行横线的垂线,交第三、四条直线,分别于、,
根据题意得,
∵,
∴,
又∵,
∴
故选:C
3.B
【分析】根据放大镜成像的特点,结合各变换的特点即可得出答案.
解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.
故选B.
4.D
解:A.当∠ABP=∠C时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
B.当∠APB=∠ABC时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
C.当时,
又∵∠A=∠A,
∴△ABP∽△ACB,
故此选项错误;
D.无法得到△ABP∽△ACB,故此选项正确.
故选:D.
5.B
解:先由四边形ABCD是正方形,AB=12,BM=5,可得MC=12﹣5=7,
根据两角对应相等的两三角形相似,得出△ABM∽△MCG,
根据相似三角形的性质得到,
故可得出CG=,再求出DG=12﹣=,
根据平行线的性质得出△MCG∽△EDG,即可得出,
即,
解得DE=.
故选B.
6.C
【分析】证明,根据题意得出,进而即可求解.
解:∵为等边三角形,
∴,
∵,,
∴,
∴
∴
∵,
∴,
∴
∵
∴,
故选:C.
7.B
【分析】连接,首先得到,,然后证明出,进而得到,然后利用三角形面积公式求出,最后利用求解即可.
解:如图所示,连接,
∵D、E分别为中点,
∴,,
∴,,,
∴,
∴,
∵,,
∴,
∴,
∵,
∴,
∴.
故选:B.
8.B
【分析】根据镜面反射性质,可求出,再利用垂直求,最后根据三角形相似的性质,即可求出答案.
解:如图所示,
由图可知,,,
∠ABC=∠CDE=900.
根据镜面的反射性质,
∴,
∴,
,
,
.
小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为,镜子与旗杆的水平距离为,
,,.
.
.
故选:B.
9.C
【分析】根据平行线分线段成比例定理即可判断A,根据相似三角形的性质即可判断B、C、D.
解:∵,
∴,△DEF∽△CBF,△ADE∽△ABC,故A不符合题意;
∴,,故B不符合题意,C符合题意;
∴,故D不符合题意;
故选C.
10.D
【分析】根据相似三角形的判定与性质进行逐一判断即可.
解:∵,
∴AD:AB=AE:AC=1:3,
∵∠A=∠A,
∴△ADE∽△ABC,
∴DE:BC=1:3,故A错误;
∵△ADE∽△ABC,
∴△ADE与△ABC的面积比为1:9,周长的比为1:3,故B和C错误;
∵△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.故D正确.
故选:D.
二、填空题
11.
【分析】黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比.其比值是一个无理数,用分数表示为,由此即可求解.
解:弦,点是靠近点的黄金分割点,设,则,
∴,解方程得,,
点是靠近点的黄金分割点,设,则,
∴,解方程得,,
∴之间的距离为,
故答案为:.
12.∠ADE=∠B(答案不唯一).
【分析】已知有一个公共角,则可以再添加一个角从而利用有两组角对应相等的两个三角形相似来判定或添加夹此角的两边对应成比例也可以判定.
解:解∶∵∠A=∠A,
∴根据两角相等的两个三角形相似,可添加条件∠ADE=∠B或∠AED=∠C证相似;
根据两边对应成比例且夹角相等,可添加条件证相似.
故答案为∶∠ADE=∠B(答案不唯一).
13.
【分析】四边形是平行四边形,则,可证明,得到,由进一步即可得到答案.
解:∵四边形是平行四边形,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
故答案为:
14.
【分析】根据题意可得,然后相似三角形的性质,即可求解.
解:∵和均为直角
∴,
∴,
∴
∵,
∴,
故答案为:.
15.27
【分析】根据矩形的性质,很容易证明∽,相似三角形之比等于对应边比的平方,即可求出的面积.
解:四边形是矩形,
,
,
,
∽,
,,
::,
::,即::,
.
故答案为:.
16.
【分析】根据位似图形的性质即可求出答案.
解:,
,
设周长为,设周长为,
和是以点为位似中心的位似图形,
.
.
和的周长之比为.
故答案为:.
17.
【分析】根据MN⊥BC,AC⊥BC,DB⊥BC,得,可得,因为,列出关于MN的方程,即可求出MN的长.
解:∵MN⊥BC,DB⊥BC,
∴AC∥MN∥DB,
∴,
∴
即,
又∵,
∴,
解得,
故填:.
18.
【分析】先根据等高的两个三角形的面积比等于边长比,得出,再根据△AOD∽△COB得出,再根据等高的两个三角形的面积比等于边长比计算即可
解:作AE⊥BC,CF⊥BD
∵
∴△ABD和△BCD等高,高均为AE
∴
∵AD∥BC
∴△AOD∽△COB
∴
∵△BOC和△DOC等高,高均为CF
∴
∴
故答案为:
三、解答题
19.
解:∵在△ABC中,AB=AC,BD=CD,
∴AD⊥BC.
又∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
20.
解:(1)证明:∵是斜边上的高.
∴,
∴,
∴
又∵
∴,
(2)∵
∴,
又
∴.
21.
解:(1)∵AB=AD,AC平分∠BAD,
∴AC⊥BD,
∴∠ACD+∠BDC=90°,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠ADC+∠BDC=90°,
∴∠BDC=∠PDC;
(2)解:过点C作CM⊥PD于点M,
∵∠BDC=∠PDC,
∴CE=CM,
∵∠CMP=∠ADP=90°,∠P=∠P,
∴△CPM∽△APD,
∴,
设CM=CE=x,
∵CE:CP=2:3,
∴PC=x,
∵AB=AD=AC=1,
∴,
解得:x=,
故AE=1﹣=.
22.
解:(1)如图,点即为所求.
(2)如图,点即为所求.
23.
解:证明:(1),
,即,
在和中,,
;
(2)由(1)已证:,
,
,,
,
解得或(不符题意,舍去),
则的长为9.
24.
解:(1)证明:因为四边形是正方形, ∴OA=OB,∠AOE=∠BOG=90°.
∵BH⊥AF,
与中, ∠AOB=∠BOG,
OA=OB, ∴△OAE ≌△OBG(ASA).
∠OAE=∠OBG,
(2)四边形是菱形,理由如下:在△ AHG与△AHB中,
∠GAH=∠BAH,
HA=HA,
∠AHG=∠AHB=90°,
∴△AHG≌△AHB(ASA),
是线段的垂直平分线,∴ 四边形是菱形.
(3) 设 菱形的边长为.
∵ 四边形是菱形,
在Rt△GOE中,由勾股定理可得,∴AC=2a=(2+)b,
.
.
