2024年山东省青岛市中考数学试卷(含答案)
文档属性
| 名称 | 2024年山东省青岛市中考数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 163.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 00:00:00 | ||
图片预览




文档简介
2024年山东省青岛市中考数学试卷
一、选择题:本题共9小题,每小题3分,共27分。在每小题给出的选项中,只有一项是符合题目要求的。
1.“海葵一号”是完全由我国自主设计建造的深水油气田“大国重器”,集原油生产、存储、外输等功能于一体,储油量达立方米将用科学记数法表示为( )
A. B. C. D.
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
3.实数,,,在数轴上对应点的位置如图所示,这四个实数中绝对值最小的是( )
A. B. C. D.
4.如图所示的正六棱柱,其俯视图是( )
A. B. C. D.
5.下列计算正确的是( )
A. B. C. D.
6.如图,将正方形先向右平移,使点与原点重合,再将所得正方形绕原点顺时针方向旋转,得到四边形,则点的对应点的坐标是( )
A.
B.
C.
D.
7.为筹备运动会,小松制作了如图所示的宣传牌,在正五边形和正方形中,,的延长线分别交,于点,,则的度数是( )
A. B.
C. D.
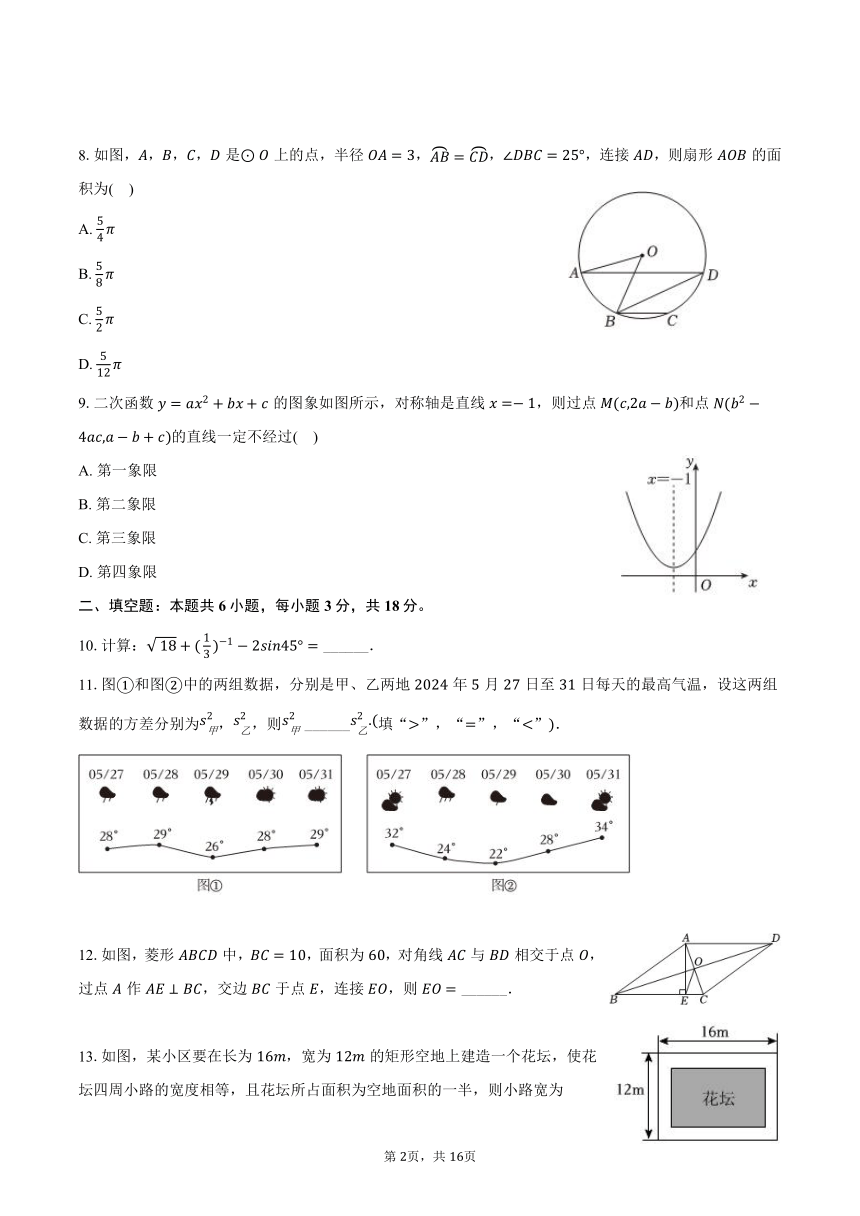
8.如图,,,,是上的点,半径,,,连接,则扇形的面积为( )
A.
B.
C.
D.
9.二次函数的图象如图所示,对称轴是直线,则过点和点的直线一定不经过( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
二、填空题:本题共6小题,每小题3分,共18分。
10.计算: ______.
11.图和图中的两组数据,分别是甲、乙两地年月日至日每天的最高气温,设这两组数据的方差分别为,,则 ______填“”,“”,“”.
12.如图,菱形中,,面积为,对角线与相交于点,过点作,交边于点,连接,则 ______.
13.如图,某小区要在长为,宽为的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路宽为______
14.如图,中,,以为直径的半圆分别交,于点,过点作半圆的切线,交于点,交的延长线于点若,,则半径的长为______.
15.如图,将边长为的正方形纸板沿虚线剪掉边长为的小正方形,得到如图的“纸板卡”,若用这样完全相同的“纸板卡”拼成正方形,最少需要______块;如图,将长、宽、高分别为,,的长方体砖块,切割掉长、宽、高分别为,,的长方体,得到如图的“直角砖块”,若用这样完全相同的“直角砖块”拼成正方体,最少需要______块
三、解答题:本题共10小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
已知:如图,四边形,为边上一点.
求作:四边形内一点,使,且点到,的距离相等.
17.本小题分
解不等式组:;
先化简,再从,,中选一个合适的数作为的值代入求值.
18.本小题分
某校准备开展“行走的课堂,生动的教育”研学活动,并计划从博物馆、动物园、植物园、海洋馆依次用字母,,,表示中选择一处作为研学地点为了解学生的选择意向,学校随机抽取部分学生进行调查,整理绘制了如下不完整的条形统计图和扇形统计图.
根据以上信息,解答下列问题:
补全条形统计图;扇形统计图中所对应的圆心角的度数为______;
该校共有名学生,请你估计该校有多少名学生想去海洋馆;
根据以上数据,学校最终将海洋馆作为研学地点研学后,学校从八年级各班分别随机抽取名学生开展海洋知识竞赛甲班名学生的成绩单位:分分别是:,,,,,,,,,;乙班名学生的成绩单位:分的平均数、中位数、众数分别是:,,根据以上数据判断______班的竞赛成绩更好填“甲”或“乙”
19.本小题分
学校拟举办庆祝“建国周年”文艺汇演,每班选派一名志愿者九年级一班的小明和小红都想参加,于是两人决定一起做“摸牌”游戏,获胜者参加规则如下:将牌面数字分别为,,的三张纸牌除牌面数字外,其余都相同背面朝上,洗匀后放在桌面上,小明先从中随机摸出一张,记下数字后放回并洗匀,小红再从中随机摸出一张若两次摸到的数字之和大于,则小明胜;若和小于,则小红胜;若和等于,则重复上述过程.
小明从三张纸牌中随机摸出一张,摸到“”的概率是______;
请用列表或画树状图的方法,说明这个游戏对双方是否公平.
20.本小题分
“滑滑梯”是同学们小时候经常玩的游戏,滑梯的坡角越小,安全性越高从安全性及适用性出发,小亮同学对所在小区的一处滑梯进行调研,制定了如下改造方案,请你帮小亮解决方案中的问题.
方案名称 滑梯安全改造
测量工具 测角仪、皮尺等
方案设计 如图,将滑梯顶端拓宽为,使,并将原来的滑梯改为图中所有点均在同一平面内,点,,在同一直线上,点,,,在同一直线上
测量数据 【步骤一】利用皮尺测量滑梯的高度;
【步骤二】在点处用测角仪测得;
【步骤三】在点处用测角仪测得.
解决问题 调整后的滑梯会多占多长一段地面?即求的长
参考数据:,,,,,
21.本小题分
为培养学生的创新意识,提高学生的动手能力,某校计划购买一批航空、航海模型已知商场某品牌航空模型的单价比航海模型的单价多元,用元购买航空模型的数量是用元购买航海模型数量的.
求航空和航海模型的单价;
学校采购时恰逢该商场“六一儿童节”促销:航空模型八折优惠若购买航空、航海模型共个,且航空模型数量不少于航海模型数量的,请问分别购买多少个航空和航海模型,学校花费最少?
22.本小题分
如图,点,,,,,为反比例函数图象上的点,其横坐标依次为,,,,,过点,,,,作轴的垂线,垂足分别为点,,,,;过点作于点,过点作于点,,过点作于点.
记的面积为,的面积为,,的面积为.
当时,点的坐标为______,
______,
______,
______用含的代数式表示;
当时, ______用含的代数式表示.
23.本小题分
如图,在四边形中,对角线与相交于点,,于点,于点,且.
求证:四边形是平行四边形;
若,当等于多少度时,四边形是矩形?请说明理由,并直接写出此时的值.
24.本小题分
月中旬,樱桃相继成熟,果农们迎来了繁忙的采摘销售季为了解樱桃的收益情况,从第天销售开始,小明对自己家的两处樱桃园连续天的销售情况进行了统计与分析:
樱桃园:
第天的单价、销售量与的关系如表:
单价元盒 销售量盒
第天
第天
第天
第天
第天
第天的单价与近似地满足一次函数关系,已知每天的固定成本为元.
樱桃园:
第天的利润元与的关系可以近似地用二次函数刻画,其图象如图:
樱桃园第天的单价是______元盒用含的代数式表示;
求樱桃园第天的利润元与的函数关系式;利润单价销售量固定成本
与的函数关系式是______;
求第几天两处樱桃园的利润之和即最大,最大是多少元?
这天中,共有______天樱桃园的利润比樱桃园的利润大
25.本小题分
如图,中,,,,中,,,边与重合,且顶点与边上的定点重合如图,从图所示位置出发,沿射线方向匀速运动,速度为;同时,动点从点出发,沿方向匀速运动,速度为与交于点,连接,设运动时间为解答下列问题:
当为何值时,点在线段的垂直平分线上?
设四边形的面积为,求与的函数关系式;
如图,过点作,交于点,与关于直线对称,连接是否存在某一时刻,使?若存在,求出的值;若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:作的平分线,以为顶点,为一边作,交于,如图:
点即为所求.
17.解:解第一个不等式得:,
解第二个不等式得:,
故原不等式组的解集为;
原式
;
,,
,,
或,
当时,原式;
当时,原式.
18.总人数:人,
组人数:;如图:
;
所对应的圆心角的度数为:;
去海洋馆:人,
即该校约有名学生想去海洋馆;
甲班名学生的成绩:,,,,,,,,,,
平均数:,众数:;中位数:,
则甲班的平均数,中位数,众数都高于乙班,则甲班的竞赛成绩更好.
19.;
游戏公平,理由如下:
根据题意列表如下:
由表可知:共有种等可能的情况数,其中两次摸到的数字之和大于的有种,两次摸到的数字之和小于的有种,
小明获胜的概率是,小红获胜的概率为,
两人获胜的概率相等,
游戏公平.
20.解:如图,过点作于,
则四边形为矩形,
,,
在中,,,
则,
,
在中,,,
则,
,
答:调整后的滑梯会多占约为的一段地面.
21.解:设航空模型的单价为元,则航海模型的单价为元,
根据题意得:,
解得,
经检验,是方程的解,也符合题意,
,
航空模型的单价为元,航海模型的单价为元;
设购买航空模型个,学校花费元,则购买航海模型个,
航空模型数量不少于航海模型数量的,
,
解得,
根据题意得:,
,
当时,取最小值,最小值为,
此时,
购买航空模型个,购买航海模型个,学校花费最少.
22.当时,,
当时,;当时,,
,,
,
,
同理:
,,
,
,
,
,
;
,
;
当时,,
,
.
23.证明:,
,
,
于点,于点,
,
,
≌,
,
,
四边形是平行四边形;
解:当等于度时,四边形是矩形,理由如下:
,,
,
是等边三角形,
,,
四边形是平行四边形,
,,
,
四边形是矩形,
,
.
24.;
根据题意可得:,
化简整理得:,
樱桃园第天的利润元与的函数关系式为:;
;
,
,
当时,有最大值,
第天两处的樱桃园的利润之和最大,最大是元;
.
25.解:当点在线段的垂直平分线上,则有,
根据题意可得:,,,
,
点在线段的垂直平分线上,
,即,
解得:,符合题意,
当为秒时,点在线段的垂直平分线上;
过点作于点,于点,连接,
则,
在中,,
根据勾股定理得:,
,,
,,
,,即,,
解得:,,
由平移可知,且,
,
,
;
过点作于点,
,
,
∽,
,即,
,,
,
,与关于直线对称,
,即,
,
,,
,
,
,
解得,故符合题意,
当为秒时,.
第1页,共1页
一、选择题:本题共9小题,每小题3分,共27分。在每小题给出的选项中,只有一项是符合题目要求的。
1.“海葵一号”是完全由我国自主设计建造的深水油气田“大国重器”,集原油生产、存储、外输等功能于一体,储油量达立方米将用科学记数法表示为( )
A. B. C. D.
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
3.实数,,,在数轴上对应点的位置如图所示,这四个实数中绝对值最小的是( )
A. B. C. D.
4.如图所示的正六棱柱,其俯视图是( )
A. B. C. D.
5.下列计算正确的是( )
A. B. C. D.
6.如图,将正方形先向右平移,使点与原点重合,再将所得正方形绕原点顺时针方向旋转,得到四边形,则点的对应点的坐标是( )
A.
B.
C.
D.
7.为筹备运动会,小松制作了如图所示的宣传牌,在正五边形和正方形中,,的延长线分别交,于点,,则的度数是( )
A. B.
C. D.
8.如图,,,,是上的点,半径,,,连接,则扇形的面积为( )
A.
B.
C.
D.
9.二次函数的图象如图所示,对称轴是直线,则过点和点的直线一定不经过( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
二、填空题:本题共6小题,每小题3分,共18分。
10.计算: ______.
11.图和图中的两组数据,分别是甲、乙两地年月日至日每天的最高气温,设这两组数据的方差分别为,,则 ______填“”,“”,“”.
12.如图,菱形中,,面积为,对角线与相交于点,过点作,交边于点,连接,则 ______.
13.如图,某小区要在长为,宽为的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路宽为______
14.如图,中,,以为直径的半圆分别交,于点,过点作半圆的切线,交于点,交的延长线于点若,,则半径的长为______.
15.如图,将边长为的正方形纸板沿虚线剪掉边长为的小正方形,得到如图的“纸板卡”,若用这样完全相同的“纸板卡”拼成正方形,最少需要______块;如图,将长、宽、高分别为,,的长方体砖块,切割掉长、宽、高分别为,,的长方体,得到如图的“直角砖块”,若用这样完全相同的“直角砖块”拼成正方体,最少需要______块
三、解答题:本题共10小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
已知:如图,四边形,为边上一点.
求作:四边形内一点,使,且点到,的距离相等.
17.本小题分
解不等式组:;
先化简,再从,,中选一个合适的数作为的值代入求值.
18.本小题分
某校准备开展“行走的课堂,生动的教育”研学活动,并计划从博物馆、动物园、植物园、海洋馆依次用字母,,,表示中选择一处作为研学地点为了解学生的选择意向,学校随机抽取部分学生进行调查,整理绘制了如下不完整的条形统计图和扇形统计图.
根据以上信息,解答下列问题:
补全条形统计图;扇形统计图中所对应的圆心角的度数为______;
该校共有名学生,请你估计该校有多少名学生想去海洋馆;
根据以上数据,学校最终将海洋馆作为研学地点研学后,学校从八年级各班分别随机抽取名学生开展海洋知识竞赛甲班名学生的成绩单位:分分别是:,,,,,,,,,;乙班名学生的成绩单位:分的平均数、中位数、众数分别是:,,根据以上数据判断______班的竞赛成绩更好填“甲”或“乙”
19.本小题分
学校拟举办庆祝“建国周年”文艺汇演,每班选派一名志愿者九年级一班的小明和小红都想参加,于是两人决定一起做“摸牌”游戏,获胜者参加规则如下:将牌面数字分别为,,的三张纸牌除牌面数字外,其余都相同背面朝上,洗匀后放在桌面上,小明先从中随机摸出一张,记下数字后放回并洗匀,小红再从中随机摸出一张若两次摸到的数字之和大于,则小明胜;若和小于,则小红胜;若和等于,则重复上述过程.
小明从三张纸牌中随机摸出一张,摸到“”的概率是______;
请用列表或画树状图的方法,说明这个游戏对双方是否公平.
20.本小题分
“滑滑梯”是同学们小时候经常玩的游戏,滑梯的坡角越小,安全性越高从安全性及适用性出发,小亮同学对所在小区的一处滑梯进行调研,制定了如下改造方案,请你帮小亮解决方案中的问题.
方案名称 滑梯安全改造
测量工具 测角仪、皮尺等
方案设计 如图,将滑梯顶端拓宽为,使,并将原来的滑梯改为图中所有点均在同一平面内,点,,在同一直线上,点,,,在同一直线上
测量数据 【步骤一】利用皮尺测量滑梯的高度;
【步骤二】在点处用测角仪测得;
【步骤三】在点处用测角仪测得.
解决问题 调整后的滑梯会多占多长一段地面?即求的长
参考数据:,,,,,
21.本小题分
为培养学生的创新意识,提高学生的动手能力,某校计划购买一批航空、航海模型已知商场某品牌航空模型的单价比航海模型的单价多元,用元购买航空模型的数量是用元购买航海模型数量的.
求航空和航海模型的单价;
学校采购时恰逢该商场“六一儿童节”促销:航空模型八折优惠若购买航空、航海模型共个,且航空模型数量不少于航海模型数量的,请问分别购买多少个航空和航海模型,学校花费最少?
22.本小题分
如图,点,,,,,为反比例函数图象上的点,其横坐标依次为,,,,,过点,,,,作轴的垂线,垂足分别为点,,,,;过点作于点,过点作于点,,过点作于点.
记的面积为,的面积为,,的面积为.
当时,点的坐标为______,
______,
______,
______用含的代数式表示;
当时, ______用含的代数式表示.
23.本小题分
如图,在四边形中,对角线与相交于点,,于点,于点,且.
求证:四边形是平行四边形;
若,当等于多少度时,四边形是矩形?请说明理由,并直接写出此时的值.
24.本小题分
月中旬,樱桃相继成熟,果农们迎来了繁忙的采摘销售季为了解樱桃的收益情况,从第天销售开始,小明对自己家的两处樱桃园连续天的销售情况进行了统计与分析:
樱桃园:
第天的单价、销售量与的关系如表:
单价元盒 销售量盒
第天
第天
第天
第天
第天
第天的单价与近似地满足一次函数关系,已知每天的固定成本为元.
樱桃园:
第天的利润元与的关系可以近似地用二次函数刻画,其图象如图:
樱桃园第天的单价是______元盒用含的代数式表示;
求樱桃园第天的利润元与的函数关系式;利润单价销售量固定成本
与的函数关系式是______;
求第几天两处樱桃园的利润之和即最大,最大是多少元?
这天中,共有______天樱桃园的利润比樱桃园的利润大
25.本小题分
如图,中,,,,中,,,边与重合,且顶点与边上的定点重合如图,从图所示位置出发,沿射线方向匀速运动,速度为;同时,动点从点出发,沿方向匀速运动,速度为与交于点,连接,设运动时间为解答下列问题:
当为何值时,点在线段的垂直平分线上?
设四边形的面积为,求与的函数关系式;
如图,过点作,交于点,与关于直线对称,连接是否存在某一时刻,使?若存在,求出的值;若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:作的平分线,以为顶点,为一边作,交于,如图:
点即为所求.
17.解:解第一个不等式得:,
解第二个不等式得:,
故原不等式组的解集为;
原式
;
,,
,,
或,
当时,原式;
当时,原式.
18.总人数:人,
组人数:;如图:
;
所对应的圆心角的度数为:;
去海洋馆:人,
即该校约有名学生想去海洋馆;
甲班名学生的成绩:,,,,,,,,,,
平均数:,众数:;中位数:,
则甲班的平均数,中位数,众数都高于乙班,则甲班的竞赛成绩更好.
19.;
游戏公平,理由如下:
根据题意列表如下:
由表可知:共有种等可能的情况数,其中两次摸到的数字之和大于的有种,两次摸到的数字之和小于的有种,
小明获胜的概率是,小红获胜的概率为,
两人获胜的概率相等,
游戏公平.
20.解:如图,过点作于,
则四边形为矩形,
,,
在中,,,
则,
,
在中,,,
则,
,
答:调整后的滑梯会多占约为的一段地面.
21.解:设航空模型的单价为元,则航海模型的单价为元,
根据题意得:,
解得,
经检验,是方程的解,也符合题意,
,
航空模型的单价为元,航海模型的单价为元;
设购买航空模型个,学校花费元,则购买航海模型个,
航空模型数量不少于航海模型数量的,
,
解得,
根据题意得:,
,
当时,取最小值,最小值为,
此时,
购买航空模型个,购买航海模型个,学校花费最少.
22.当时,,
当时,;当时,,
,,
,
,
同理:
,,
,
,
,
,
;
,
;
当时,,
,
.
23.证明:,
,
,
于点,于点,
,
,
≌,
,
,
四边形是平行四边形;
解:当等于度时,四边形是矩形,理由如下:
,,
,
是等边三角形,
,,
四边形是平行四边形,
,,
,
四边形是矩形,
,
.
24.;
根据题意可得:,
化简整理得:,
樱桃园第天的利润元与的函数关系式为:;
;
,
,
当时,有最大值,
第天两处的樱桃园的利润之和最大,最大是元;
.
25.解:当点在线段的垂直平分线上,则有,
根据题意可得:,,,
,
点在线段的垂直平分线上,
,即,
解得:,符合题意,
当为秒时,点在线段的垂直平分线上;
过点作于点,于点,连接,
则,
在中,,
根据勾股定理得:,
,,
,,
,,即,,
解得:,,
由平移可知,且,
,
,
;
过点作于点,
,
,
∽,
,即,
,,
,
,与关于直线对称,
,即,
,
,,
,
,
,
解得,故符合题意,
当为秒时,.
第1页,共1页
同课章节目录
