2024-2025学年湖南师大附中博才实验中学九年级(上)入学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年湖南师大附中博才实验中学九年级(上)入学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 76.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-21 10:33:24 | ||
图片预览



文档简介
2024-2025学年湖南师大附中博才实验中学九年级(上)入学数学试卷
一、选择题:本题共9小题,每小题3分,共27分。在每小题给出的选项中,只有一项是符合题目要求的。
1.对于二次函数的图象,下列说法正确的是( )
A. 开口向下 B. 对称轴是直线
C. 顶点坐标是 D. 与轴有两个交点
2.如图,在菱形中,点,分别是,的中点,如果,那么菱形的周长为( )
A.
B.
C.
D.
3.若,是一元二次方程的两个实数根,则的值为( )
A. B. C. D.
4.对于一次函数,下列说法错误的是( )
A. 随的增大而减小 B. 图象与轴交点为
C. 图象经过第一、二、四象限 D. 图象经过点
5.六位同学的年龄分别是、、、、、岁,关于这组数据,正确说法是( )
A. 平均数是 B. 中位数是 C. 方差是 D. 众数是
6.关于的一元二次方程有两个不相等的实数根,则的值可能是( )
A. B. C. D.
7.如图,矩形中,对角线,相交于点,若,则( )
A.
B.
C.
D.
8.随着中考结束,初三某毕业班的每一个同学都向其他同学赠送一张自己的照片留作纪念,全班共送了张照片,若该班有名同学,则根据题意可列出方程为( )
A. B.
C. D.
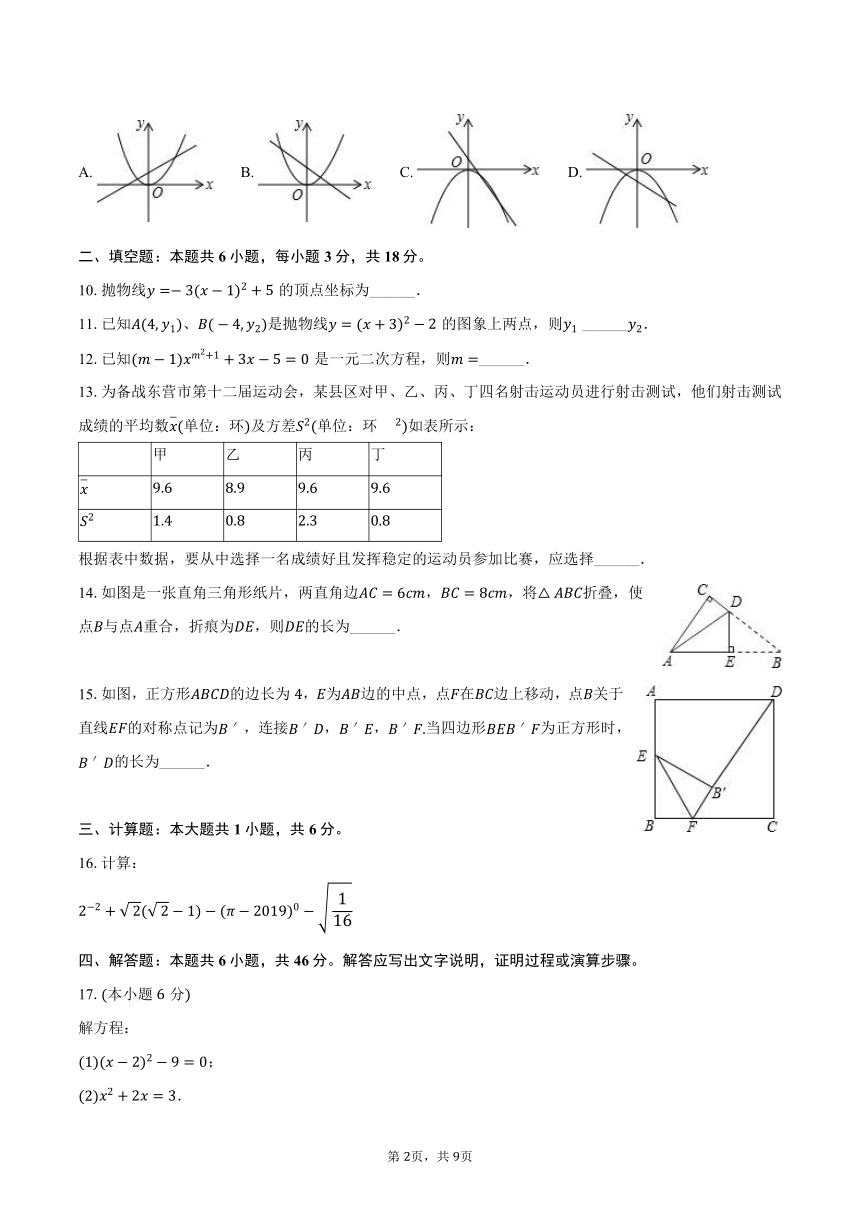
9.函数与的图象可能是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
10.抛物线的顶点坐标为______.
11.已知、是抛物线的图象上两点,则 ______.
12.已知是一元二次方程,则______.
13.为备战东营市第十二届运动会,某县区对甲、乙、丙、丁四名射击运动员进行射击测试,他们射击测试成绩的平均数单位:环及方差单位:环如表所示:
甲 乙 丙 丁
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择______.
14.如图是一张直角三角形纸片,两直角边,,将折叠,使点与点重合,折痕为,则的长为______.
15.如图,正方形的边长为,为边的中点,点在边上移动,点关于直线的对称点记为,连接,,当四边形为正方形时,的长为______.
三、计算题:本大题共1小题,共6分。
16.计算:
四、解答题:本题共6小题,共46分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
解方程:
;
.
18.本小题分
已知抛物线,经过点和.
求、的值;
将该抛物线向上平移个单位长度,再向右平移个单位长度,得到新的抛物线,直接写出新的抛物线相应的函数表达式.
19.本小题分
如图,在中,,平分交于点,过作交于点,交于点,连接.
求证:四边形是菱形;
若,,求的长.
20.本小题分
如图,直线交轴和轴于点和点,点在轴上,连接.
求点和点的坐标;
若点是直线上一点,若的面积为,求点的坐标;
21.本小题分
某县著名传统土特产品“豆笋”、“豆干”以“浓郁豆香,绿色健康”享誉全国,深受广大消费者喜爱已知件豆笋和件豆干进货价为元,件豆笋和件豆干进货价为元.
分别求出每件豆笋、豆干的进价;
某特产店计划用不超过元购进豆笋、豆干共件,且豆笋的数量不低于豆干数量的,该特产店有哪几种进货方案?
若该特产店每件豆笋售价为元,每件豆干售价为元,在的条件下,怎样进货可使该特产店获得利润最大,最大利润为多少元?
22.本小题分
定义:对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点四边形”,如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”
【概念理解】
在已经学过的“平行四边形;矩形;菱形;正方形”中,______是“中方四边形”填序号;
【性质探究】
如图,若四边形是“中方四边形”,观察图形,线段和线段有什么关系,并证明你的结论;
【问题解决】
如图,以锐角的两边,为边长,分别向外侧作正方形和正方形连结,,,依次连接四边形的四边中点得到四边形求证:四边形是“中方四边形”.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.丁
14.
15.
16.解:原式
17.解:方程整理得:,
则,即,或,
解得:,;
,
则,
,
或,
,.
18.解:解:将点和代入抛物线得:.
解得:,
,;
原函数的表达式为:,向上平移个单位长度,再向右平移个单位长度,得平移后的新函数表达式为:即.
19.证明:,,
四边形是平行四边形.
平分,
.
,
.
.
.
平行四边形是菱形;
解:,,
.
设,
.
.
在中,
解得,
.
20.解:将代入得,
,
解得,
所以点坐标为.
将代入得,
,
所以点坐标为.
由,得,
,
又因为的面积为,
则,
解得,
当时,
;
当时,
;
所以点的坐标为或.
21.解:设每件豆笋的进价为元,每件豆干的进价为元,
由题意得:,
解得:,
每件豆笋的进价为元,每件豆干的进价为元;
设购进豆笋件,则购进豆干件,
由题意可得:,
解得:,且为整数,
该特产店有以下三种进货方案:
当时,,即购进豆笋件,购进豆干件,
当时,,即购进豆笋件,购进豆干件,
当时,,即购进豆笋件,购进豆干件,
设总利润为元,
则,
,
随的增大而增大,
当时,取得最大值,最大值为,
购进豆笋件,购进豆干件可使该特产店获得利润最大,最大利润为元.
22.;
解:,;理由如下:
四边形是“中方四边形”,
是正方形且、、、分别是、、、的中点,
,,,,,,
,;
证明:如图,连接交于,连接交于,
四边形各边中点分别为、、、,
、,,分别是、、、的中位线,
,,,,,,,,
,,,,
四边形是平行四边形,
四边形和四边形都是正方形,
,,,
又,
,
即,
在和中,
,
≌,
,,
又,,
,
平行四边形是菱形,
,
.
又,,
,
,
又,,
.
菱形是正方形,
即原四边形是“中方四边形”.
第1页,共1页
一、选择题:本题共9小题,每小题3分,共27分。在每小题给出的选项中,只有一项是符合题目要求的。
1.对于二次函数的图象,下列说法正确的是( )
A. 开口向下 B. 对称轴是直线
C. 顶点坐标是 D. 与轴有两个交点
2.如图,在菱形中,点,分别是,的中点,如果,那么菱形的周长为( )
A.
B.
C.
D.
3.若,是一元二次方程的两个实数根,则的值为( )
A. B. C. D.
4.对于一次函数,下列说法错误的是( )
A. 随的增大而减小 B. 图象与轴交点为
C. 图象经过第一、二、四象限 D. 图象经过点
5.六位同学的年龄分别是、、、、、岁,关于这组数据,正确说法是( )
A. 平均数是 B. 中位数是 C. 方差是 D. 众数是
6.关于的一元二次方程有两个不相等的实数根,则的值可能是( )
A. B. C. D.
7.如图,矩形中,对角线,相交于点,若,则( )
A.
B.
C.
D.
8.随着中考结束,初三某毕业班的每一个同学都向其他同学赠送一张自己的照片留作纪念,全班共送了张照片,若该班有名同学,则根据题意可列出方程为( )
A. B.
C. D.
9.函数与的图象可能是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
10.抛物线的顶点坐标为______.
11.已知、是抛物线的图象上两点,则 ______.
12.已知是一元二次方程,则______.
13.为备战东营市第十二届运动会,某县区对甲、乙、丙、丁四名射击运动员进行射击测试,他们射击测试成绩的平均数单位:环及方差单位:环如表所示:
甲 乙 丙 丁
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择______.
14.如图是一张直角三角形纸片,两直角边,,将折叠,使点与点重合,折痕为,则的长为______.
15.如图,正方形的边长为,为边的中点,点在边上移动,点关于直线的对称点记为,连接,,当四边形为正方形时,的长为______.
三、计算题:本大题共1小题,共6分。
16.计算:
四、解答题:本题共6小题,共46分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
解方程:
;
.
18.本小题分
已知抛物线,经过点和.
求、的值;
将该抛物线向上平移个单位长度,再向右平移个单位长度,得到新的抛物线,直接写出新的抛物线相应的函数表达式.
19.本小题分
如图,在中,,平分交于点,过作交于点,交于点,连接.
求证:四边形是菱形;
若,,求的长.
20.本小题分
如图,直线交轴和轴于点和点,点在轴上,连接.
求点和点的坐标;
若点是直线上一点,若的面积为,求点的坐标;
21.本小题分
某县著名传统土特产品“豆笋”、“豆干”以“浓郁豆香,绿色健康”享誉全国,深受广大消费者喜爱已知件豆笋和件豆干进货价为元,件豆笋和件豆干进货价为元.
分别求出每件豆笋、豆干的进价;
某特产店计划用不超过元购进豆笋、豆干共件,且豆笋的数量不低于豆干数量的,该特产店有哪几种进货方案?
若该特产店每件豆笋售价为元,每件豆干售价为元,在的条件下,怎样进货可使该特产店获得利润最大,最大利润为多少元?
22.本小题分
定义:对于一个四边形,我们把依次连接它的各边中点得到的新四边形叫做原四边形的“中点四边形”,如果原四边形的中点四边形是个正方形,我们把这个原四边形叫做“中方四边形”
【概念理解】
在已经学过的“平行四边形;矩形;菱形;正方形”中,______是“中方四边形”填序号;
【性质探究】
如图,若四边形是“中方四边形”,观察图形,线段和线段有什么关系,并证明你的结论;
【问题解决】
如图,以锐角的两边,为边长,分别向外侧作正方形和正方形连结,,,依次连接四边形的四边中点得到四边形求证:四边形是“中方四边形”.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.丁
14.
15.
16.解:原式
17.解:方程整理得:,
则,即,或,
解得:,;
,
则,
,
或,
,.
18.解:解:将点和代入抛物线得:.
解得:,
,;
原函数的表达式为:,向上平移个单位长度,再向右平移个单位长度,得平移后的新函数表达式为:即.
19.证明:,,
四边形是平行四边形.
平分,
.
,
.
.
.
平行四边形是菱形;
解:,,
.
设,
.
.
在中,
解得,
.
20.解:将代入得,
,
解得,
所以点坐标为.
将代入得,
,
所以点坐标为.
由,得,
,
又因为的面积为,
则,
解得,
当时,
;
当时,
;
所以点的坐标为或.
21.解:设每件豆笋的进价为元,每件豆干的进价为元,
由题意得:,
解得:,
每件豆笋的进价为元,每件豆干的进价为元;
设购进豆笋件,则购进豆干件,
由题意可得:,
解得:,且为整数,
该特产店有以下三种进货方案:
当时,,即购进豆笋件,购进豆干件,
当时,,即购进豆笋件,购进豆干件,
当时,,即购进豆笋件,购进豆干件,
设总利润为元,
则,
,
随的增大而增大,
当时,取得最大值,最大值为,
购进豆笋件,购进豆干件可使该特产店获得利润最大,最大利润为元.
22.;
解:,;理由如下:
四边形是“中方四边形”,
是正方形且、、、分别是、、、的中点,
,,,,,,
,;
证明:如图,连接交于,连接交于,
四边形各边中点分别为、、、,
、,,分别是、、、的中位线,
,,,,,,,,
,,,,
四边形是平行四边形,
四边形和四边形都是正方形,
,,,
又,
,
即,
在和中,
,
≌,
,,
又,,
,
平行四边形是菱形,
,
.
又,,
,
,
又,,
.
菱形是正方形,
即原四边形是“中方四边形”.
第1页,共1页
同课章节目录
